
Preview text:
ĐỀ 4
ĐỀ KIỂM TRA GIỮA HỌC KỲ I NĂM HỌC 2024-2025 MÔN: TOÁN 12
Thời gian làm bài: 90 phút
PHẦN I. Trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi
câu hỏi thí sinh chỉ chọn 1 phương án.
Câu 1. (TD-Biết) Cho hàm số y = f (x) có bảng biến như sau:
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. (1;5). B. (3;+) . C. ( 1 − ; ) 3 . D. (0;4) .
Câu 2. (GQ- Biết ) Cho hàm số y = f (x) có đồ thị như hình vẽ . Hàm số nghịch biến trên khoảng nào
trong các khoảng sau đây? A. (0;2) . B. (2;+). C. (0;+). D. ( ) ;1 − .
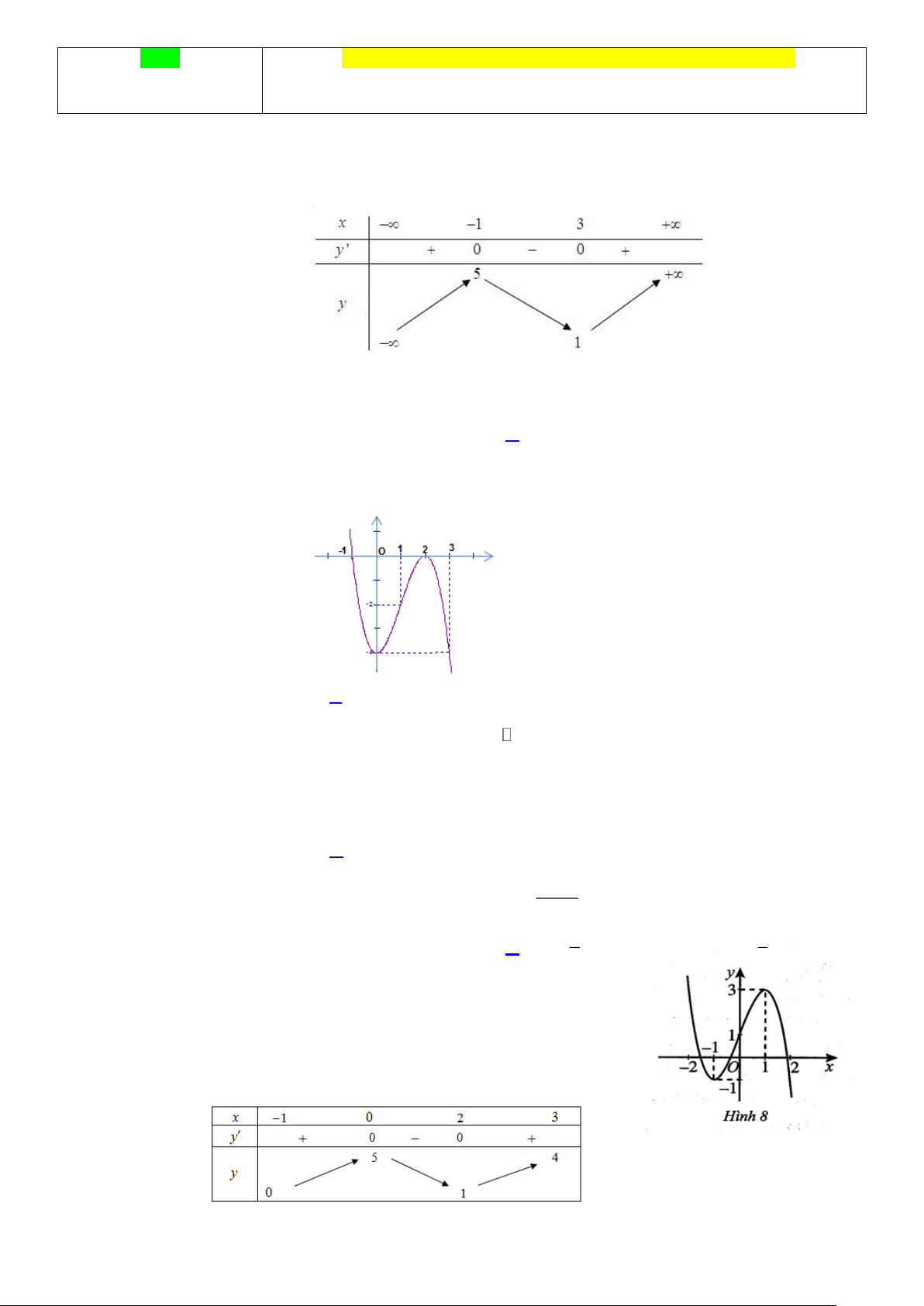
Câu 3. ( TD- Biết )Cho hàm số y = f (x) liên tục trên và có đồ thị như Hình 8. Gọi m, M lần lượt là
giá trị nhỏ nhất và giá trị lớn nhất của hàm số f ( x) trên đoạn 2 − ;
2 . Phát biểu nào sau đây đúng? A. m = 2 − , M = 2 .
B. m = 1, M = 3.
C. m = 3, M = 1. D. m = 1 − , M = 3 . 3x −1
Câu 4. (TD- Hiểu ) Tìm giá trị lớn nhất M của hàm số y = trên đoạn 0;2. x − 3 1 1 A. M = 5. B. M = 5 − . C. M = . D. M = − . 3 3
Câu 5. (TD- Hiểu )Cho hàm số y = f (x) liên tục và có bảng biến thiên trong đoạn 1 − ;
3 như hình bên. Gọi M là giá trị nhỏ nhất của
hàm số y = f (x) trên đoạn 1 − ; 3 . Tìm mệnh đề đúng? Trang 1
A. M = f (0) .
B. M = f ( ) 3 .
C. M = f (2) .
D. M = f (− ) 1 .
Câu 6. (TD- Biết )Cho hàm số y = f (x) có đồ thị (C) và lim f (x) = − , lim f (x) = 2 − . Số tiệm x→− x→+
cận ngang của (C) là A. 0. B. 2. C. 1. D. 3. 2 − x
Câu 7. (TD- Hiểu )Tiệm cận đứng của đồ thị hàm số y = là x + 3 A. x = 2 . B. x = 3 − . C. y = 1 − . D. y = −3 .
Câu 8. (TD- Hiểu )Cho hàm số y = f (x) xác định trên \ 1
− , liên tục trên mỗi khoảng xác định và
có bảng biến thiên như hình vẽ. Số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y = f (x) là: A. 1. B. 2. C. 0. D. 3.
Câu 9. (TD- Biết )Đồ thị sau đây là của hàm số nào? A. 3 y = x − 3x − 4 . B. 3 2 y = −x + 3x − 4 . 2x −1 2 x − x + 2 C. y = . D. y = . x +1 x −1
Câu 10. (TD- Biết )Bảng biến thiên sau đây là của hàm số nào? x +1 2 x + 3 A. 3 y = −x + 2x −1. B. 2 y = x − x + 2 . C. y = . D. y = . x − 2 2 + x
Câu 11. ( GQ- Hiểu ) Cho hàm số y = f (x) có đồ thị như hình vẽ dưới đây. Tọa độ giao điểm của đồ thị với trục tung là: Trang 2 A. (0;2) . B. (2;0) . C. (1;0) . D. (0; ) 1 .
Câu 12. ( TD- Biết ) Một chất điểm chuyển động theo phương trình s(t) 3 2 = t
− +18t + t + 3, trong đó t
tính bằng giây và s tính bằng mét. Chất điểm có vận tốc tức thời v(t) = s(t) bao nhiêu m/s tại
thời điểm t = 1 giây? A. 34. B. 21. C. 35. D. 33.
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 13 đến câu 16. trong mỗi ý
(A,B,C,D) ở mỗi câu thí sinh chọn đúng hoặc sai.
Câu 13. Cho hàm số y = f (x) liên tục trên R và có bảng biến thiên như sau.
A. Hàm số nghịch biến (0;2) .
B. Hàm số đồng biến (0;+).
C. Hàm số có giá trị lớn nhất trên 3 − : 2 bằng 4.
D. Hàm số có giá trị nhỏ nhất trên (0; ) 3 bằng 2.
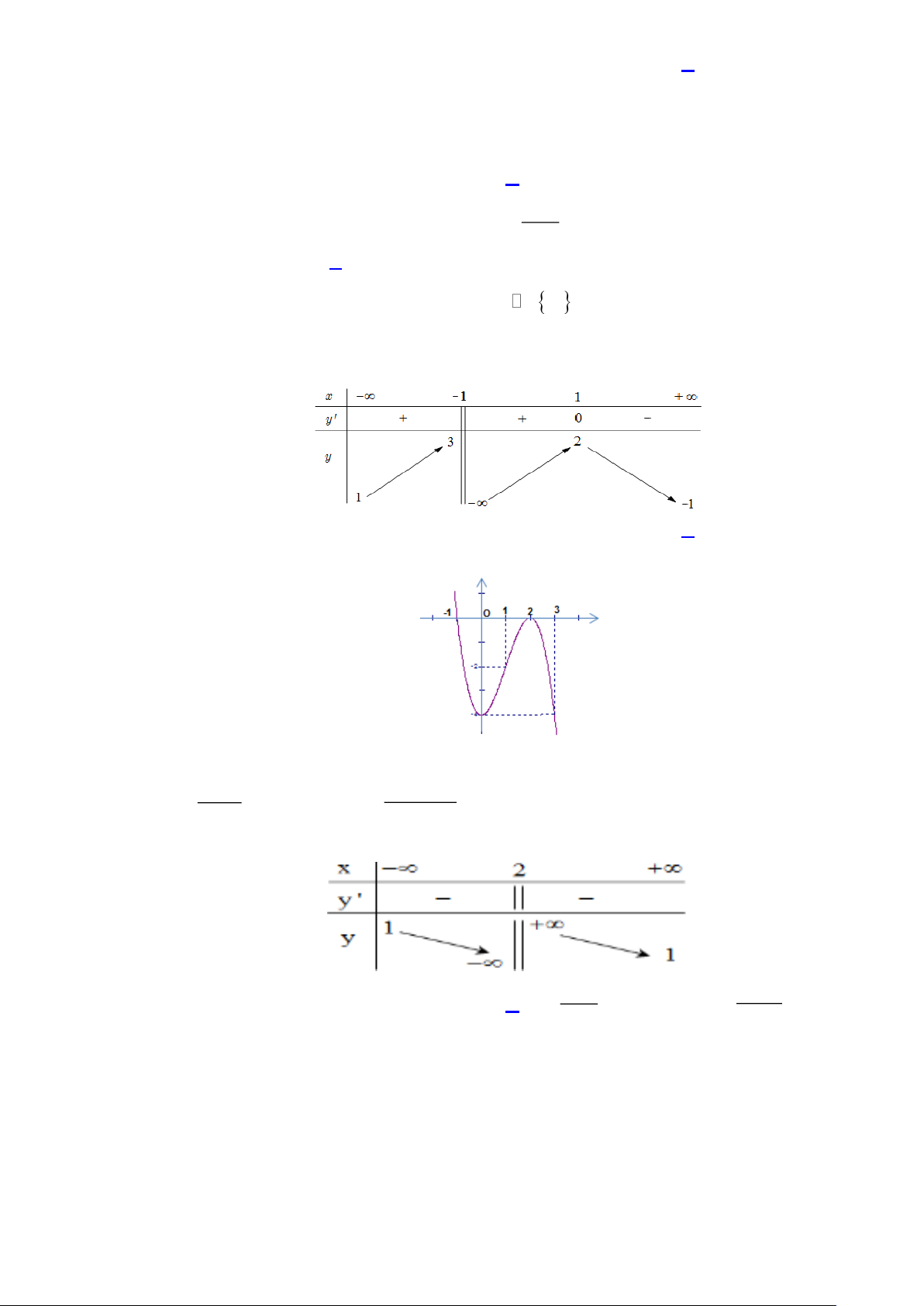
Câu 14. Cho hàm số y = f (x) có đồ thị nḥư Hình 5.
A. Đồ thị không có tiệm cận đứng.
B. Đồ thị có tiệm cận xiên qua gốc tọa độ.
C. Đường tiệm cận xiên có phương trình y =x. ax + b
D. Đồ thị hình 5 là hàm số có dạng y = . x c +d .
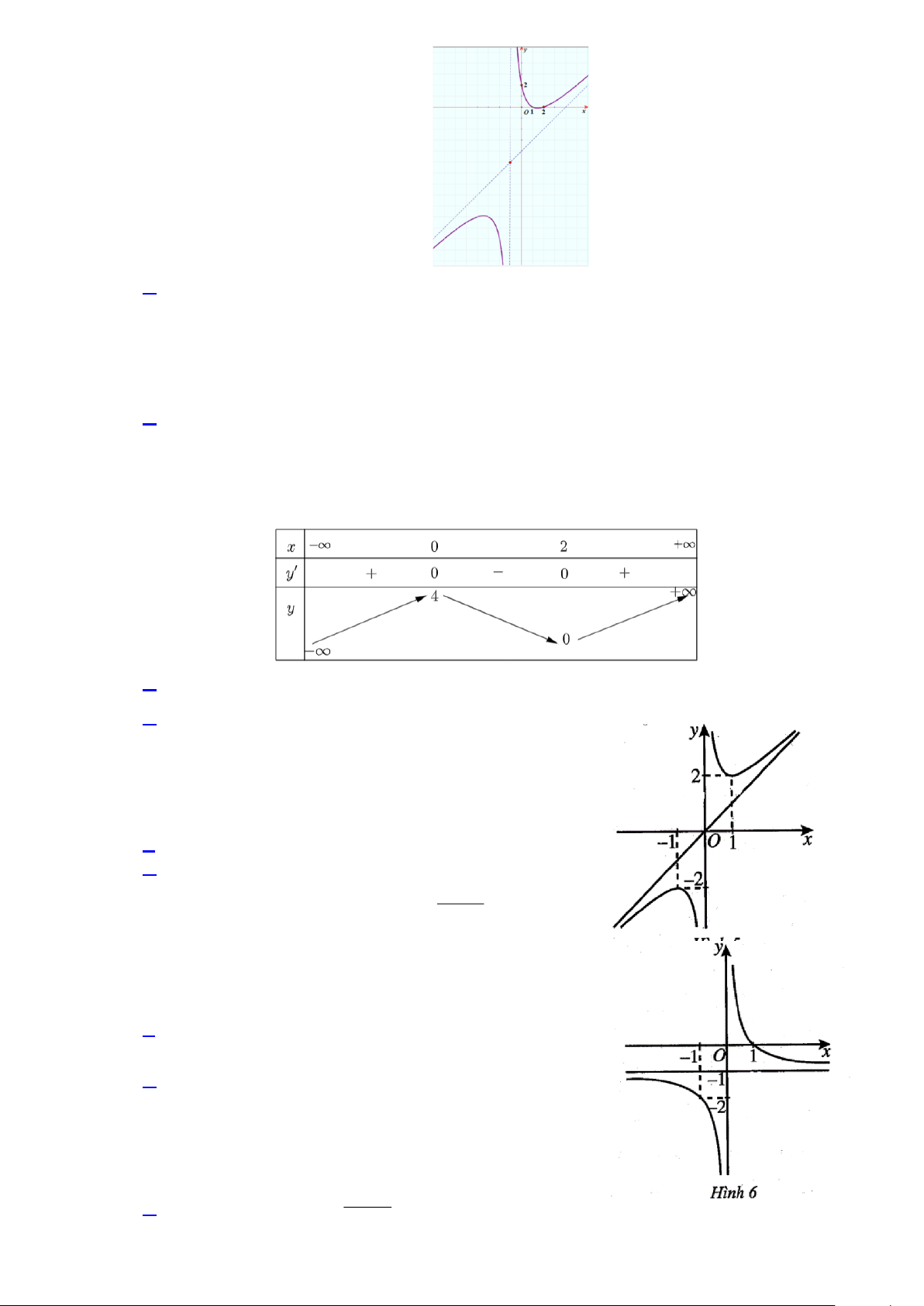
Câu 15. Cho hàm số y = f (x) có đồ thị như Hình 6.
A. Đồ thị hàm số có một tiệm cận.
B. Đồ thị hàm số có tiệm cận ngang y = −1.
C. Hàm số nghịch biến trên R.
D. Đồ thị hàm số cắt trục hành tại điểm (1;0).
Câu 16. Trong 200 gam dung dịch muối nồng độ 15%, giả sử thêm
vào dung dịch x (gam ) muối tinh khiết và được dung dịch
có nồng độ f (x)%. ax + b
A. Hàm số f ( x) có dạng . ( d a − bc ) 0 . cx + d Trang 3
B. Đạo hàm của hàm số f (x) luôn nhận giá trị âm trên khoảng (0; + ∞).
C. Thêm càng nhiều gam muối tinh khiết thì nồng độ phần trăm càng tăng không giới hạn .
D. Giới hạn của f (x) khi x dần đến dương vô cực bằng 100.
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 17 đến câu 22.
Câu 17. Kính viễn vọng không gian Hubble được đưa vào vũ trụ ngày 24/4/1990 bằng tàu con thoi
Discovery. Vận tốc của tàu con thoi trong sứ mệnh này, từ lúc cất cánh tại thời điểm t = 0(s)
cho đến khi tên lửa đẩy được phóng đi tại thời điểm t = 126 (s) cho bởi hàm số sau đây: v(t) 3 2
= 0,001302t – 0,09029t + 23, (v được tính bằng ft/s, 1 feet = 0,3048 m) Gọi ( ;
a b) là khoảng thời gian gia tốc v(t) của tàu con thoi sẽ tăng tính từ thời điểm cất cánh
cho đến khi tên lửa đẩy được phóng đi. Tính T = a + b ?
Câu 18. Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật
không nắp có thể tích bằng 3
288dm . Đáy bể là hình chữ nhật có chiều
dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500 nghìn đồng/ 2
m . Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí
thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê
nhân công xây dựng bể đó là bao nhiêu?.
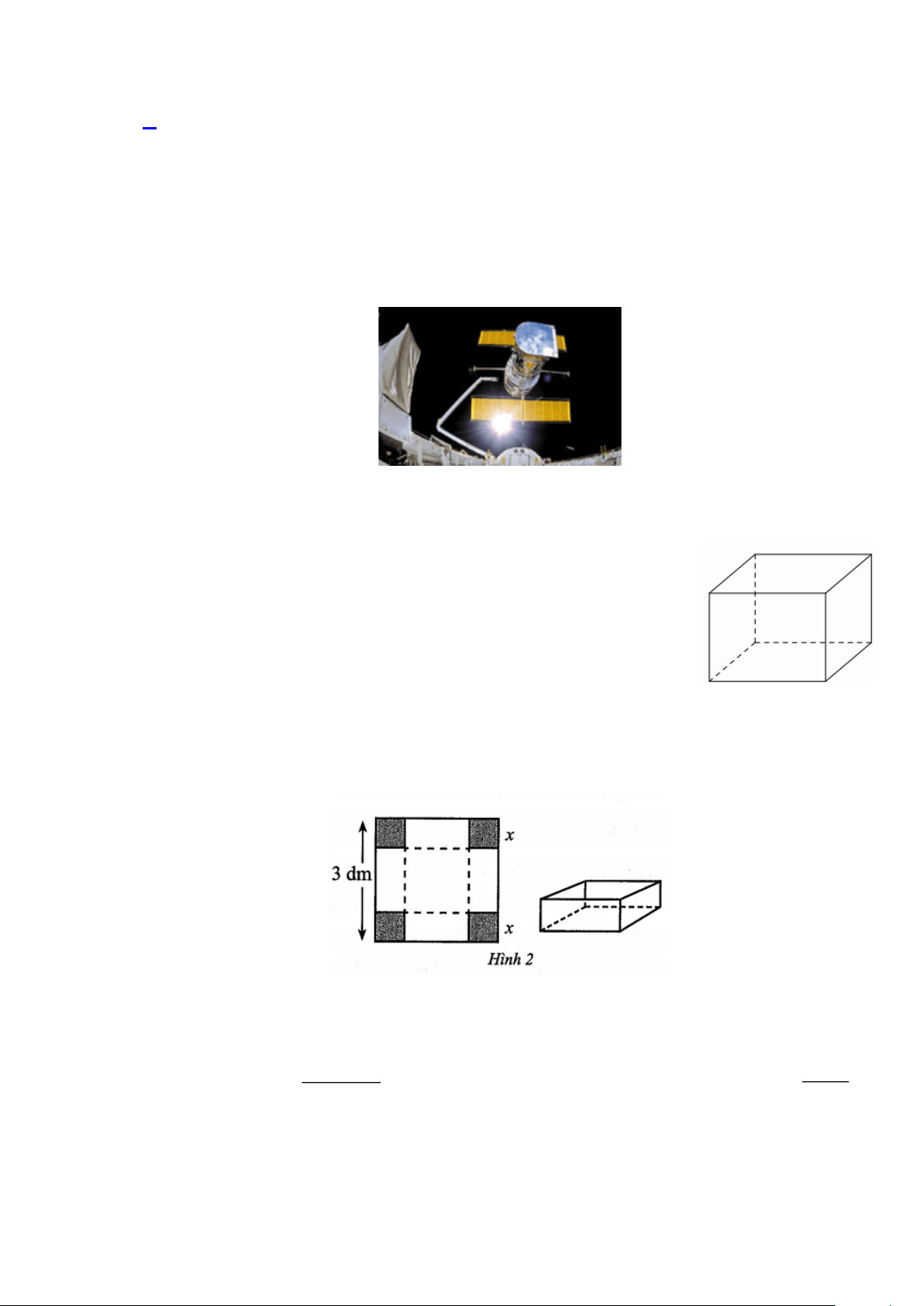
Câu 19. Cho một tấm nhôm có dạng hình vuông cạnh 3dm . Bác Tùng cắt ở bốn góc bốn hình vuông
cùng có độ dài cạnh bằng x(dm) , rồi gấp tấm nhôm lại như Hình 2 để được một cái hộp có
dạng hình hộp chữ nhật không có nắp.
Gọi V là thể tích của khối hộp đó tính theo x(dm) . Giá trị lớn nhất của V là bao nhiêu decimét khối?. 2 x − 3x +1 m
Câu 20. Cho hàm số f ( x) = các hằng số a, ,
b c, d, m . Hàm số có dạng y = ax + b + . x +1 cx + d Tính 2 2
a + b − c bằng:.
Câu 21. Một công ty sản xuất một sản phẩm. Bộ phận tài chính của công ty đưa ra hàm giá bán là
p(x) =1000 − 25x , trong đó p(x) (triệu đồng) là giá bán của mỗi sản phẩm mà tại giá bán này Trang 4
có x sản phẩm được bán ra. Khi doanh thu đạt giá trị lớn nhất bằng 10000 triệu đồng thì có
bao nhiêu sản phẩm được bán ra?.
Câu 22. Một công ty kinh doanh bất động sản có 20 căn hộ cho thuê. Biết rằng nếu cho thuê mỗi căn hộ
với giá 2 triệu đồng/1 tháng thì tất cả các căn hộ đều có người thuê. Nhưng cứ mỗi lần tăng giá
cho thuê mỗi căn hộ thêm 200 nghìn đồng/1 tháng thì có thêm một căn hộ bị bỏ trống. Hỏi
công ty nên cho thuê mỗi căn hộ bao nhiêu triệu đồng một tháng để tổng số tiền thu được là lớn nhất? .Hết.
ĐÁP ÁN ĐỀ KIỂM TRA GIỮA KỲ I NĂM HỌC 2024-2025
PHẦN I. Trắc nghiệm nhiều phương án lựa chọn
Mỗi câu trả lời đúng 0,25 điểm Câu 1 2 3 4 5 6 7 8 9 10 11 12 Chọn C B D C D C B D B C A A
PHẦN II. Câu trắc nghiệm đúng sai.
Điểm tối đa mỗi câu là 1 điểm
- Chọn được 1 ý đúng trong 1 câu hỏi được 0,1 điểm
- Chọn được 2 ý đúng trong 1câu hỏi được 0,25 điểm
- Chọn được 3 ý đúng trong 1 câu hỏi được 0,5 điểm
- Chọn được 4 ý đúng trong 1 câu hỏi được 1 điểm Câu 13 Câu 14 Câu 15 Câu 16 A Đ A S A S A Đ B S B Đ B Đ B S C Đ C Đ C S C S D S D S D Đ D Đ
PHẦN III. Câu trắc nghiệm trả lời ngắn
Mỗi câu trả lời đúng 0.5 điểm Câu Câu 17 Câu 18 Câu 19 Câu 20 Câu 21 Câu 22 Kq 149 1080 2 16 20 3 Trang 5 Lời giải 15
Câu 16. Trong 200 gam dung dịch muối nồng độ 15% có 200.
= 30 (gam) muối tinh khiết. 100
Khi thêm x (gam) muối tinh khiết vào 200 gam dung dịch muối nồng độ 15% thì có (x + 30)
(gam ) muối tinh khiết. Khi đó, ta có hàm số là 100 x + 30 A. f (x) ( ) = . x + 200 17000
B) Ta có f '( x) =
0, x 0;+ . Suy ra b) sai. 2 ( ) (x + 200)
C) Vì f (x) đồng biến trên khoảng ( 0;+) nên khi x tăng thì f (x) tăng. Nghĩa là khi thêm càng
nhiều gam muối tinh khiết thì dung dịch có nồng độ phần trăm càng tăng. x + 30 100 x + 30
Vì x + 30 x + 200 với mọi x (0;+) nên
1 dẫn đến f (x) ( ) = 100. Nghĩa x + 200 x + 200
là nồng độ phần trăm không vượt quá 100% khi cho thêm nhiều gam muối tinh khiết vào. Suy ra c) sai. 100 x + 30
d) Ta có : lim f (x) ( ) = lim
=100. Suy ra d) đúng. x→+ x→+ x + 200 Câu 17 :Đáp án: 149
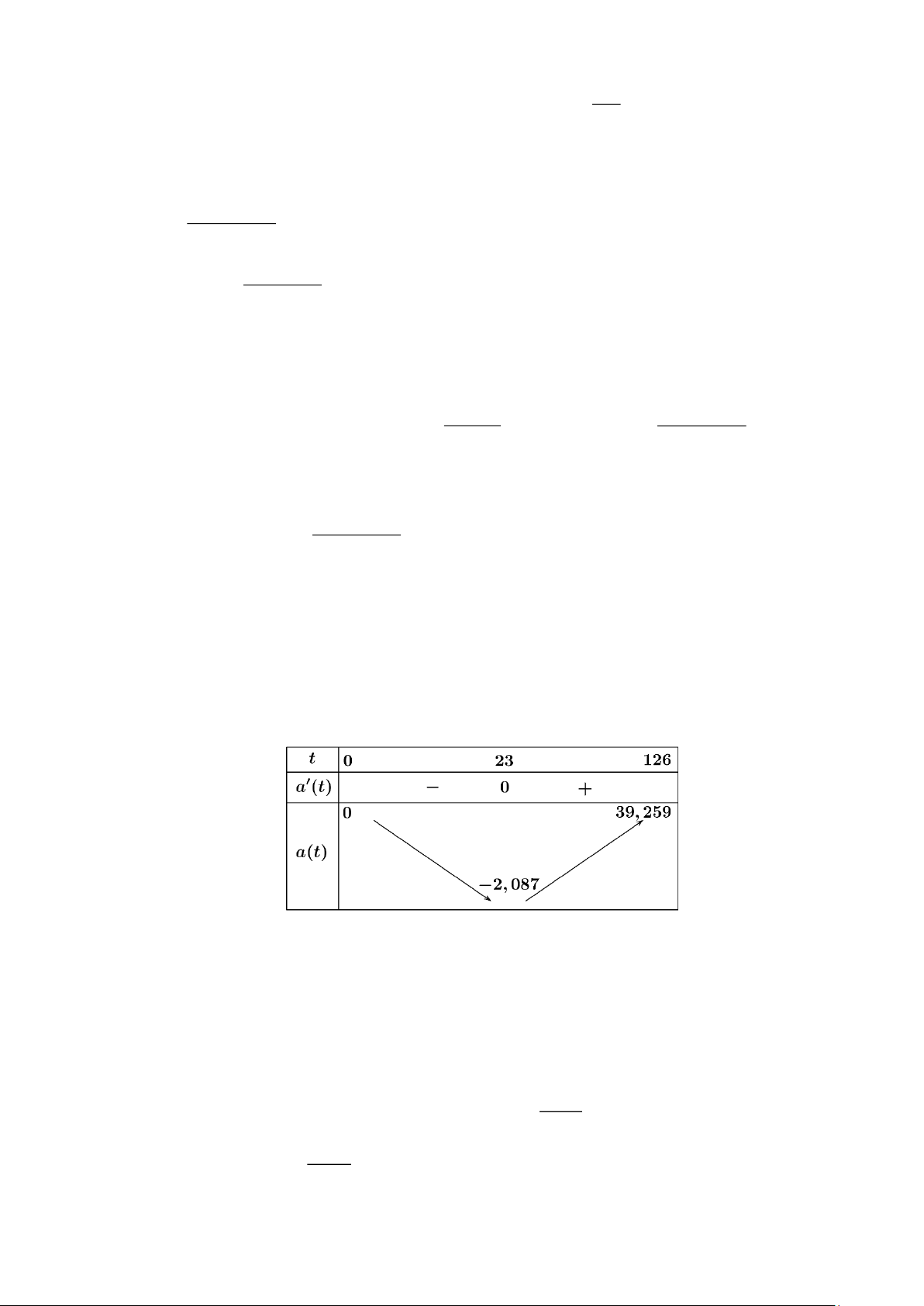
Xét hàm số vận tốc của tàu con thoi v(t) 3 2
= 0,001302t – 0,09029t + 23 với t 0;126.
Gia tốc của tàu con thoi là a(t) = v(t) 2 = 0,003906t 0 − ,18058t .
Ta có a(t) = 0,007812t – 0,18058 = 0 t 23.
Bảng biến thiên của hàm số a(t)như sau:
Vậy gia tốc của tàu con thoi sẽ tăng trong khoảng thời gian (23 ;
s 126s) tính từ thời điểm cất cánh
cho đến khi tên lửa đẩy được phóng đi.
Do đó:T = a + b = 23+126 =149. Câu 18 . Đáp án: 1080 x(x 0) Gọi
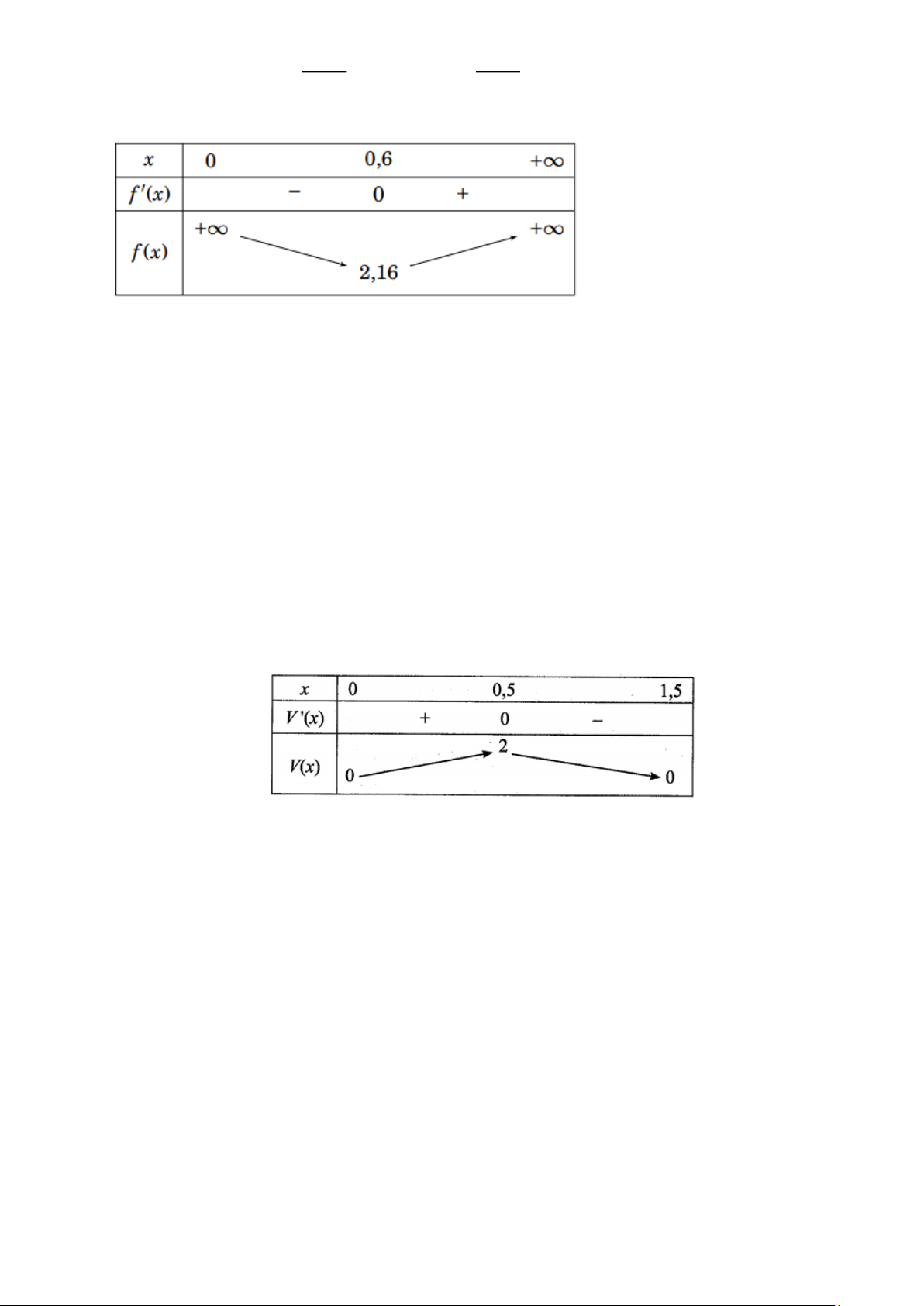
là chiều rộng của đáy bể. 0,144
Khi đó chiều dài của đáy bể là 2x và chiều cao của bể là 2 x . 0,864 2 2x + Diện tích cần xây là x Trang 6 0,864 f ( x) 0,864 2 = 2x +
f ( x) = 4x − = 0 x = 0,6 Xét hàm số x có 2 x f ( x)
Bảng biến thiên của hàm số như sau:
min f (x) = f (0,6) = 2,16
Từ bảng biên thiên ta có
Vậy chi phí thấp nhất để thuê nhân công xây bể là: 500.2,16 = 1080 nghìn đồng.
Câu 19. Ta thấy độ dài x(dm) của cạnh hình vuông bị cắt thoả mãn điều kiện 0 x 1,5 .
Thể tích của khối hộp là V ( x) = x( − x)2 3 2
với 0 x 1,5 .
Ta phải tìm x 0;1,5 sao cho V (x có giá trị lơn nhất. 0 ) 0 ( )
Ta có: V ( x) = ( − x)2 3 2
− 4x(3− 2x) = (3− 2x)(3− 6x) = 3(3− 2x)(1− 2x) .
Trên khoảng (0;1,5),V(x) = 0 khi x = 0,5.
Báng biến thiên của hàm số V ( x) như sau:
Căn cứ bảng biến thiên, ta thấy: Trên khoảng (0;1,5), hàm số V ( x) đạt giá trị lón nhất bằng 2 tại
x = 0,5 . Vây giá trị lớn nhất của V là 3 2dm . Câu 21.
Ta có doanh thu của công ty bằng giá bán của mỗi sản phẩm nhân với số sản phẩm được bán ra. Suy
ra hàm doanh thu của công ty là f (x) = . x p(x).
Ta có f (x) = x p(x) = x( − x) 2 . 1000 25 = 2 − 5x +1000x.
Suy ra đạo hàm f (x) = 5 − 0x +1000.
f (x) = 0 5
− 0x +1000 = 0 x = 20
Vậy f (x) = 0 có nghiệm là x = 20 .
Lập BBT của hàm số f (x) 2 = 2
− 5x +1000x ta có f (x) 2 = 2
− 5x +1000x đạt giá trị lớn nhất là 10000 tại x = 20 . Trang 7
Vậy doanh thu đạt giá trị lớn nhất bằng 10000 triệu đồng, khi đó có 20 sản phẩm được bán ra Câu 22
Cứ tăng thêm 200 nghìn đồng vào giá thuê một căn hộ trên một tháng thì có một căn hộ bị bỏ trống.
Gọi số lần tăng 200 nghìn đồng vào giá thuê một căn hộ trên một tháng là x.
Khi đó x cũng là số căn hộ bị bỏ trống.
Tổng số tiền công ty thu được lúc này là T (x) = ( + x)( − x) 2 2000 200 20 = 2
− 00x + 2000x + 40000 (nghìn đồng).
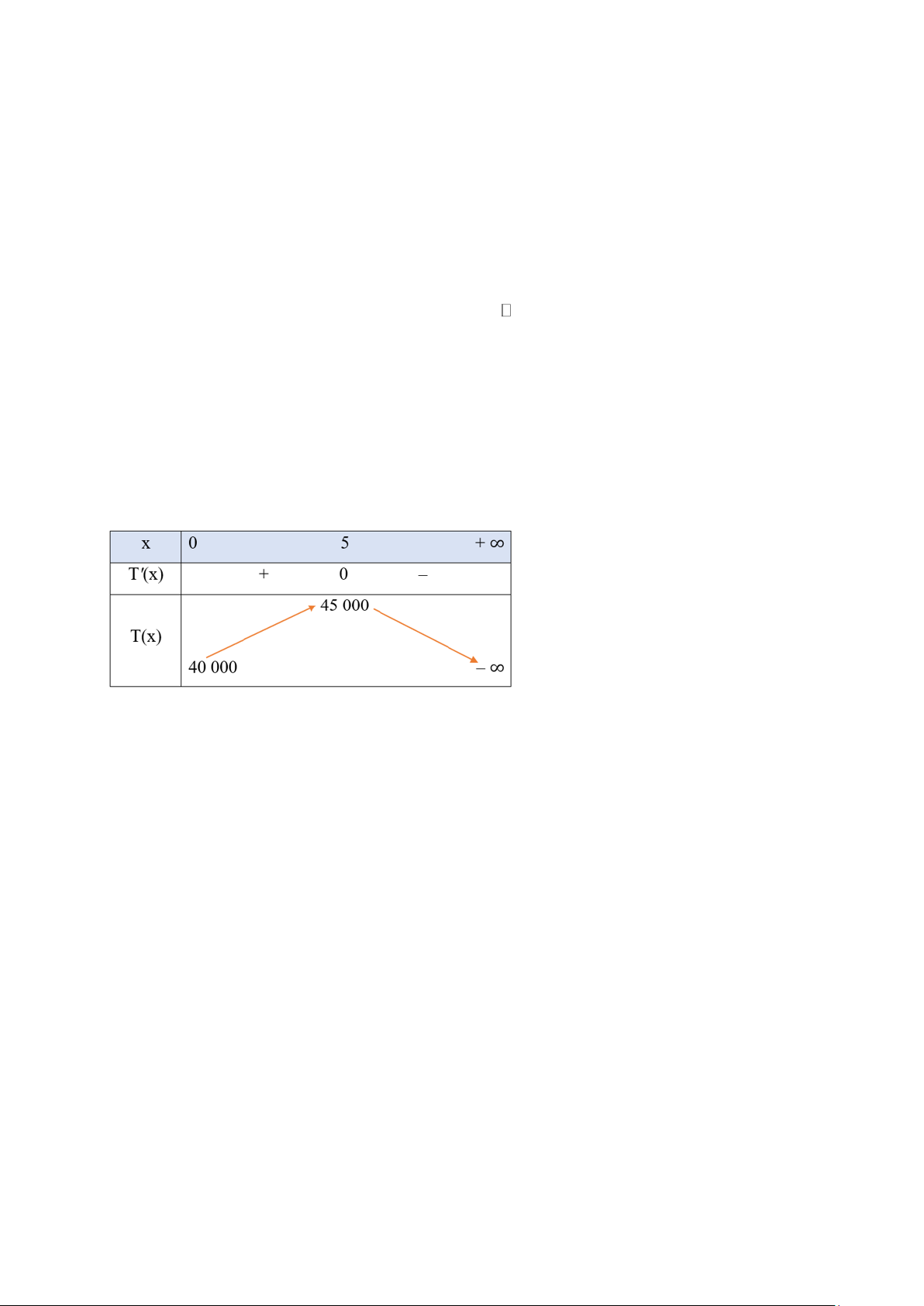
Xét hàm số T (x) 2 = 2
− 00x + 2000x + 40000với * x T '(x) 2 = 400 − x + 2000 T '(x) = 0 2 400 − x + 2000 = 0 x = 5(nhan)
Bảng biến thiên của hàm số T (x) như sau:
Căn cứ vào bảng biến thiên trên, ta thấy hàm số T (x) đạt giá trị lớn nhất bằng 45000 khi x = 5.
Khi đó, số tiền tăng lên khi cho thuê một căn hộ là 200.5 =1000 nghìn đồng = 1 triệu đồng.
Vậy công ty nên cho thuê mỗi căn hộ 3 triệu đồng/1 tháng thì tổng số tiền thu được là lớn nhất. Trang 8




