Đề thi giữa HK1 Toán 7 năm 2020 – 2021 trường chuyên Hà Nội – Amsterdam

Sáng thứ Tư ngày 28 tháng 10 năm 2020, Tổ Toán – Tin trường THPT chuyên Hà Nội – Amsterdam tổ chức kỳ thi kiểm tra chất lượng giữa học kì 1 môn Toán 7 năm học 2020 – 2021.

46 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 7

Môn: Toán 7

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
T
RƯỜNG THPT CHUYÊN
HÀ NỘI - AMSTERDAM
Tổ Toán - Tin học
THCS.TOANMATH.com
Câu 1. (3,0 điểm) Tính
a)
17 21
5. .4
10 15 13 3
−
+−
b)
3
3 5 4 3 5 27 5
:.
8 32 5 5 8 32 4
−− −

+ −− + +


Câu 2. (3 điểm)
a) Tìm tất cả các số hữu tỉ
x
, biết rằng:
2
2 14
3
5 5 25
x

− −=


b) Tì
m tất cả các số hữu tỉ
x
, biết rằng:
41 1
:2 1
33 2
x− −=
c
)
T
ìm các số
a
,
b
,
biết
253abc= =
và
44abc+−=−
Câu 3.
(3,0 điểm)
Cho tam giác
,ABC
Ax là tia phân giác của
BAC
. Từ C kẻ đường thẳng song song
với Ax, cắt tia đối của tia AB tại D. Kẻ tia Ay là phân giác của
DAC
. Trên nửa mặt
phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho
zAD ADC=
.
a) Ch
ứng minh
.ADC ACD=
b) C
hứng minh
.Ay DC⊥
c) Ch
ứng minh Ax và Az là hai tia đối nhau.
Câu 4. (1,0 điểm)
a) Tì
m tất cả các số nguyên
n
để biểu thức
10 7
51
n
A
n
+
=
−
nhận giá trị nguyên.
b) Tính giá
trị biểu thức
222 2
3 2 4 2 5 2 101 2
. . ...
2 2 3 3 4 4 100 100
B
 
=−−− −
 
 
HẾT
ĐỀ THI GIỮA HỌC KÌ I
NĂM
HỌC 2020 - 2021
MÔN TOÁN - LỚP 7
Thời gian làm bài: 60 phút (không kể thời gian phát đề)
-----------------------------------------
Câu 1. (3,0 điểm) Tính
a)
17 21
5. .4
10 15 13 3
−
+−
b)
3
3 5 4 3 5 27 5
:.
8 32 5 5 8 32 4
−− −−

+ −− + +


Lời giải
a)
1 7 2 1 3 14 2 13 11 2 7
5. .4 5. . 5.
10 15 13 3 30 30 13 3 30 3 6
−−
+ − = + − = −=
b)
3
3 5 4 3 5 27 5
:.
8 32 5 5 8 32 4
−− −−

+ −− + +


3
3 5 5 3 5 27 5
..
8 32 4 5 8 32 4
−− −−
 
= + −− + +
 
 
3
3 5 5 27 5 3
.
8 32 8 32 4 5
−− −

= + + + −−


27
125
=
Câu 5. (3 điểm)
a) Tìm tất cả các số hữu tỉ
x
, biết rằng:
2
2 14
3
5 5 25
x

− −=


b) Tì
m tất cả các số hữu tỉ
x
, biết rằng:
41 1
:2 1
33 2
x− −=
c
)
T
ìm các số
,,abc
biết
253abc= =
và
44abc+−=−
Lời giải
a)
2
2 14
3
5 5 25
x

− −=


2
29
3
5 25
x

⇔− =


23
3
55
23
3
55
x
x
−=
⇔
−=−
T
RƯỜNG THPT CHUYÊN
HÀ NỘI - AMSTERDAM
Tổ Toán - Tin học
THCS.TOANMATH.com
ĐỀ THI GIỮA HỌC KÌ I
NĂM
HỌC 2020 - 2021
MÔN TOÁN - LỚP 7
Thời gian làm bài: 60 phút (không kể thời gian phát đề)
-----------------------------------------
1
3
5
31
x
x
= −
⇔
=
1
15
1
3
x
x
= −
⇔
=
Vậy
1
3
x =
hoặc
1
15
x = −
b)
41 1
:2 1
33 2
x− −=
1 41
:2 1
3 32
x⇔ −= −
15
:2 1
36
x⇔ −=
15
21 :
36
x⇔ −=
2
21
5
x⇔ −=
2
21
5
2
21
5
x
x
−=
⇔
−=−
7
2
5
3
2
5
x
x
=
⇔
=
7
10
3
10
x
x
=
⇔
=
Vậy
7
10
x =
hoặc
3
10
x =
c)
253abc= =
và
44abc+−=−
Ta có
253
253
30 30 30 15 6 10
a b c abc
abc==⇒ ==⇒==
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
44
4
15 6 10 15 6 10 11
a b c abc+− −
= = = = = −
+−
4
15
60
4 24
6
40
4
10
a
a
b
b
c
c
= −
= −

⇒ =−⇒ =−


= −
= −
Vậy
60a = −
,
24b = −
,
40c = −
Câu 3. (3,0 điểm)
Cho tam giác
,ABC
Ax là tia phân giác của
BAC
. Từ C kẻ đường thẳng song song
với Ax, cắt tia đối của tia AB tại D. Kẻ tia Ay là phân giác của
DAC
. Trên nửa mặt
phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho
zAD ADC=
.
a) Chứng minh
.ADC ACD=
b) Ch
ứng minh
.Ay DC⊥
c) Ch
ứng minh Ax và Az là hai tia đối nhau.
Lời giải
a) Ta có:
//CD Ax
, (gt)
⇒
ACD CAx=
(so le trong) (1)
BAx ADC=
(đồng vị) (2)
mà
2
BAC
CAx BAx= =
(Ax là phân giác) (3)
Từ (1), (2), (3) ⇒
BAx ADC ACD= =
Vậy
ADC ACD=
b)
+ Ta có:
2
DAC
DAy CAy= =
(Vì
Ay
là phân giác góc CAD) (4)
2
BAC
CAx BAx= =
(Vì
Ax
là tia phân giác của góc
BAC
)
(5)
Từ (4), (5) ⇒
180
90
2222
=+= °= =
°
+=
DAC BAC BAD
xAy CAy CAx
Ay Ax⇒⊥
Mà
//CD Ax
⇒
Ay CD⊥
( Từ vuông góc đến song song)
c) Ta có:
zAD ADC=
(gt)
mà
//Ax DC
180⇒ +=°ADC DAx
(2 góc trong cùng phía )
180⇒+=°DAx DAz
180⇒=°xAz
Nên
Ax
và
Az
là hai tia đối nhau
Câu 6. (1,0 điểm)
a) Tì
m tất cả các số nguyên
n
để biểu thức
10 7
51
n
A
n
+
=
−
nhận giá trị nguyên.
b) Tính giá
trị biểu thức
222 2
3 2 4 2 5 2 101 2
. . ...
2 2 3 3 4 4 100 100
B
 
=−−− −
 
 
L
ời giải
a) Ta có:
10 7 10 2 9 2(5 1) 9 9
2
51 51 51 51 51
nn n
A
n n nn n
+ −+ −
= = = +=+
− − −− −
Để
A
nguyên thì
9
51n −
phải nguyên nên
{ }
(5 1) (9) 9; 3; 1;1; 3; 9nU−∈ =−−−
Ta có bảng sau:
51n −
9−
3−
1−
1
3
9
n
8
()
5
l
−
2
()
5
l
−
0( )tm
2
()
5
l
4
()
5
l
2( )tm
Vậy
{ }
0;2n∈
thì
A
nguyên
b)
222 2
3 2 4 2 5 2 101 2
. . ...
2 2 3 3 4 4 100 100
B
 
=−−− −
 
 
222 2
4 10 18 10098
. . ...
2 3 4 100
B
 
=
 
 
22 2 2
1.4 2.5 3.6 99.102
. . ...
2 3 4 100
B
 
=
 
 
222 2
(1.2.3...99).(4.5.6...102)
2 .3 .4 ...100
B =
101.102
100.2.3
B =
1717
100
B =
HẾT
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT CHUYÊN
ĐỀ THI GIỮA HỌC KÌ I HÀ NỘI - AMSTERDAM NĂM HỌC 2020 - 2021 Tổ Toán - Tin học MÔN TOÁN - LỚP 7
Thời gian làm bài: 60 phút (không kể thời gian phát đề) THCS.TOANMATH.com
-----------------------------------------
Câu 1. (3,0 điểm) Tính 1 − 7 2 1 a) 5. + − .4 10 15 13 3 3  3 − 5   4 −   3   5 − 27   5  b) + : − − + + .            8 32   5   5   8 32   4  Câu 2. (3 điểm) 2  2  1 4
a) Tìm tất cả các số hữu tỉ x , biết rằng: − 3x − =    5  5 25 4 1 1
b) Tìm tất cả các số hữu tỉ x , biết rằng: − : 2x −1 = 3 3 2
c) Tìm các số a , b , c biết 2a = 5b = 3c và a + b − c = 44 − Câu 3. (3,0 điểm)
Cho tam giác ABC, Ax là tia phân giác của 
BAC . Từ C kẻ đường thẳng song song
với Ax, cắt tia đối của tia AB tại D. Kẻ tia Ay là phân giác của 
DAC . Trên nửa mặt
phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho  =  zAD ADC . a) Chứng minh  =  ADC AC . D
b) Chứng minh Ay ⊥ DC.
c) Chứng minh Ax và Az là hai tia đối nhau. Câu 4. (1,0 điểm) 10n + 7
a) Tìm tất cả các số nguyên n để biểu thức A = nhận giá trị nguyên. 5n −1
b) Tính giá trị biểu thức  3 2   4 2   5 2   101 2  B = − . − . − ... −         2 2 2 2
 2 2   3 3   4 4  100 100  HẾTTRƯỜNG THPT CHUYÊN
ĐỀ THI GIỮA HỌC KÌ I HÀ NỘI - AMSTERDAM NĂM HỌC 2020 - 2021 Tổ Toán - Tin học MÔN TOÁN - LỚP 7
Thời gian làm bài: 60 phút (không kể thời gian phát đề) THCS.TOANMATH.com
-----------------------------------------
Câu 1. (3,0 điểm) Tính 1 − 7 2 1 a) 5. + − .4 10 15 13 3 3  3 − 5   4 −   3   5 − 27   5 −  b) + : − − + + .            8 32   5   5   8 32   4  Lời giải 1 − 7 2 1 3 − 14 2 13 11 2 7 a) 5. + − .4 = 5. + − . = 5. − = 10 15 13 3 30 30 13 3 30 3 6 3  3 − 5   4 −   3   5 − 27   5 −  b) + : − − + + .            8 32   5   5   8 32   4  3  3 − 5   5 −   3   5 − 27   5 −  = + . − − + + .            8 32   4   5   8 32   4  3  3 − 5 5 − 27   5 −   3  = + + + . − −        8 32 8 32   4   5  27 = 125 Câu 5. (3 điểm) 2  2  1 4
a) Tìm tất cả các số hữu tỉ x , biết rằng: − 3x − =    5  5 25 4 1 1
b) Tìm tất cả các số hữu tỉ x , biết rằng: − : 2x −1 = 3 3 2
c) Tìm các số a,b, c biết 2a = 5b = 3c và a + b − c = 44 − Lời giải 2  2  1 4 a) − 3x − =    5  5 25 2  2  9 ⇔ − 3x =    5  25 2 3 − 3x = 5 5 ⇔ 2 3  −3x = − 5 5  1 3x = −  ⇔ 5  3x = 1  1 x = −  15 ⇔  1 x =  3 1 1
Vậy x = hoặc x = − 3 15 4 1 1 b) − : 2x −1 = 3 3 2 1 4 1 ⇔ : 2x −1 = − 3 3 2 1 5 ⇔ : 2x −1 = 3 6 1 5 ⇔ 2x −1 = : 3 6 2 ⇔ 2x −1 = 5  2 2x −1 =  5 ⇔  2 2x −1= −  5  7 2x =  5 ⇔  3 2x =  5  7 x =  10 ⇔  3 x =  10 7 3 Vậy x = hoặc x = 10 10
c) 2a = 5b = 3c và a + b − c = 44 − 2a 5b 3c a b c
Ta có 2a = 5b = 3c ⇒ = = ⇒ = = 30 30 30 15 6 10
Áp dụng tính chất của dãy tỉ số bằng nhau ta có: a b c
a + b − c 44 − = = = = = 4 − 15 6 10 15 + 6 − 10 11  a = 4 − 15  a = 60 − b  ⇒  = 4 − ⇒ b  = 24 − 6  c = 40 −   c = 4 − 10  Vậy a = 60 − , b = 24 − , c = 40 − Câu 3. (3,0 điểm)
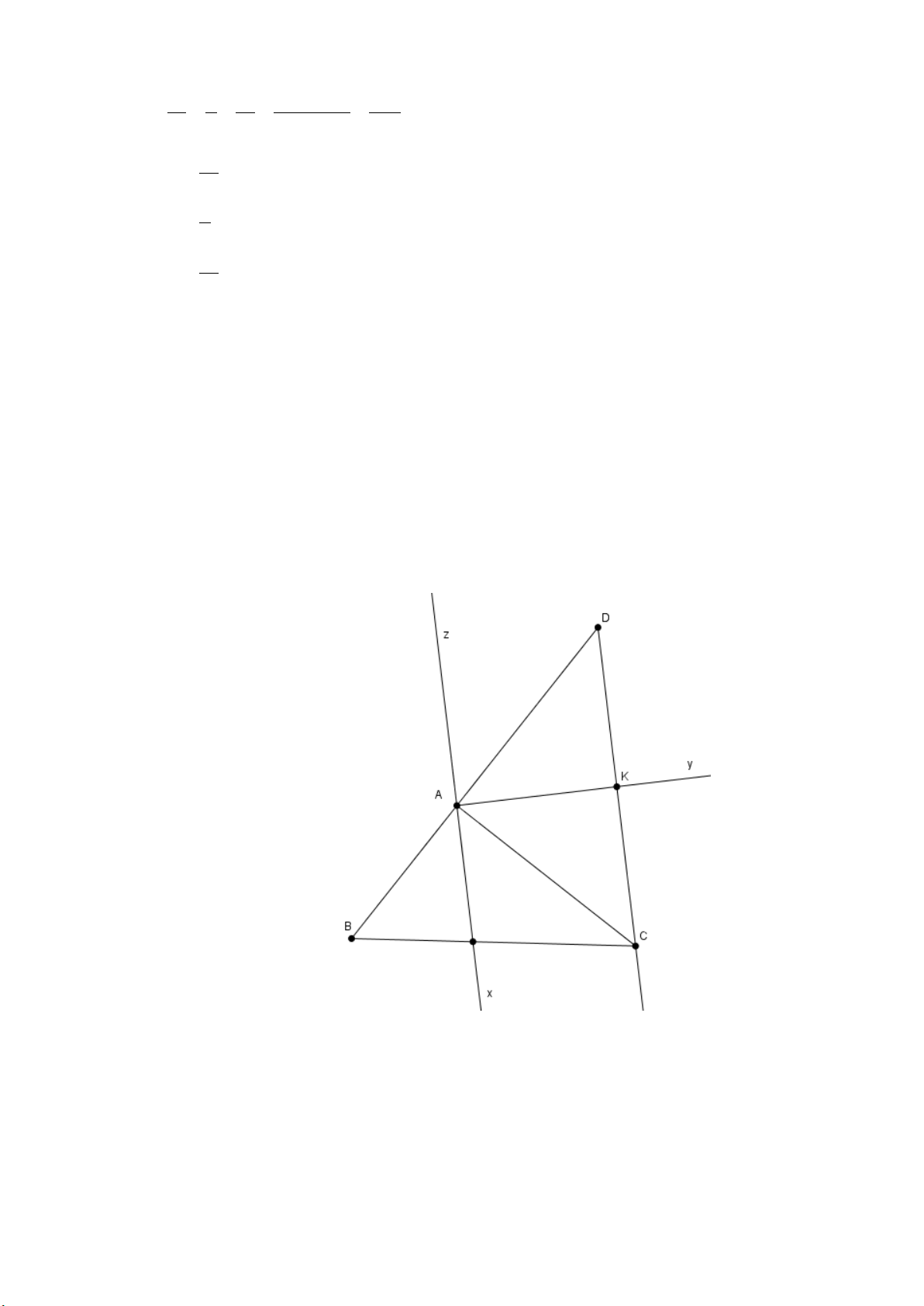
Cho tam giác ABC, Ax là tia phân giác của 
BAC . Từ C kẻ đường thẳng song song
với Ax, cắt tia đối của tia AB tại D. Kẻ tia Ay là phân giác của 
DAC . Trên nửa mặt
phẳng bờ AD không chứa điểm C, vẽ tia Az sao cho  =  zAD ADC . a) Chứng minh  =  ADC AC . D
b) Chứng minh Ay ⊥ DC.
c) Chứng minh Ax và Az là hai tia đối nhau. Lời giải a) Ta có: CD// Ax , (gt) ⇒  =  ACD CAx (so le trong) (1)  =  BAx ADC (đồng vị) (2) BAC mà  =   CAx BAx = (Ax là phân giác) (3) 2
Từ (1), (2), (3) ⇒  =  =  BAx ADC ACD Vậy  =  ADC ACD b) DAC + Ta có:  =   DAy CAy =
(Vì Ay là phân giác góc CAD) (4) 2  =   BAC CAx BAx =
(Vì Ax là tia phân giác của góc BAC ) 2 (5) DAC BAC BAD ° Từ (4), (5) ⇒  xAy =  CAy +     180 CAx = + = = = 90° 2 2 2 2 ⇒ Ay ⊥ Ax Mà CD// Ax
⇒ Ay ⊥ CD ( Từ vuông góc đến song song) c) Ta có:  =  zAD ADC (gt)
mà Ax// DC ⇒  ADC + 
DAx = 180° (2 góc trong cùng phía ) ⇒  DAx +  DAz = 180° ⇒  xAz = 180°
Nên Ax và Az là hai tia đối nhau Câu 6. (1,0 điểm) 10n + 7
a) Tìm tất cả các số nguyên n để biểu thức A = nhận giá trị nguyên. 5n −1
b) Tính giá trị biểu thức  3 2   4 2   5 2   101 2  B = − . − . − ... −         2 2 2 2
 2 2   3 3   4 4  100 100  Lời giải 10n + 7 10n − 2 + 9 2(5n −1) 9 9 a) Ta có: A = = = + = 2 + 5n −1 5n −1 5n −1 5n −1 5n −1 Để 9 A nguyên thì
(5n −1) ∈U (9) = 9 − ; 3 − ; 1 − ;1;3;9
5n − phải nguyên nên { } 1 Ta có bảng sau: 5n −1 9 − 3 − 1 − 1 3 9 8 − 2 − 2 4 n (l) (l) 0(tm) (l) (l) 2(tm) 5 5 5 5 Vậy n ∈{0; } 2 thì A nguyên b)  3 2   4 2   5 2   101 2  B = − . − . − ... −         2 2 2 2
 2 2   3 3   4 4  100 100 
 4  10   18  10098  B = . . ...         2 2 2 2
 2   3   4   100 
1.4   2.5   3.6   99.102  B = . . ...         2 2 2 2
 2   3   4   100  (1.2.3...99).(4.5.6...102) B = 2 2 2 2 2 .3 .4 ...100 101.102 B = 100.2.3 1717 B = 100  HẾT
Document Outline

  • de-thi-giua-hk1-toan-7-nam-2020-2021-truong-chuyen-ha-noi-amsterdam