
Preview text:
UBND HUYỆN HIỆP HOÀ
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
P HÒNG GIÁO DỤC VÀ ĐÀO TẠO
Năm học 2023 – 2024 MÔN: TOÁN 7
Thời gian làm bài: 90 phút, không kể thời gian giao
I. TRẮC NGHIỆM (5 điểm): Chọn chữ cái in hoa đứng trước câu trả lời đúng nhất?
Câu 1: Tỉ lệ tăng dân số Việt Nam trong một số năm gần đây được cho trong bảng sau: Năm 1991 1995 1999 2003 2007 2011 2015 2019 Tỉ lệ % 1,86 1,65 1,51 1,17 1,09 1,24 1,12 1,15
Tỉ lệ gia tăng dân số thấp nhất là năm nào? A. 2019 . B. 2015 . C. 2007 . D. 1991.
Câu 2: Các môn thể thao ưa thích của tất cả học sinh lớp 7A được ghi lại trong bảng sau, biết mỗi
bạn chỉ thích một môn. Môn thể thao
Cầu lông Bóng bàn Bóng đá Đá cầu Bóng rổ Các môn khác Số bạn ưa thích 8 3 18 4 6 2 Số học sinh lớp 7A là: A. 18. B. 41. C. 40 . D. 39.
Câu 3: Đa thức bậc 6 một biến có hai hạng tử mà hệ số cao nhất là 5, hệ số tự do là 1 − . Đó là đa thức A. 3 6x −1. B. 6 5x −1. C. 3 6x +1 D. 6 5x +1 Câu 4: Cho P ∆ QR = DE ∆ F , biết 0
P = 32 ;QR = 3cm . Khi đó: A. 0
D = 32 ; DE = 3cm . B. 0
D = 32 ; EF = 3cm . C. 0
E = 32 ; EF = 3cm . D. 0
F = 32 ; DF = 3cm .
Câu 5: Cho điểm D nằm trên đường trung trực của đoạn thẳng AB. Khẳng định đúng là
A. DA = BD .
B. DA > DB .
C. DA < DB .
D. DA ≥ DB . Câu 6: . Cho A ∆ BC và N
∆ PM có BC = PM ; = 0
B P = 90 . Cần thêm một điều kiện gì để A ∆ BC và N
∆ PM bằng nhau theo trường hợp cạnh huyền – cạnh góc vuông?
A. BA = PM .
B. BA = PN .
C. CA = MN . D. = A N .
Câu 7: Bạn Nam đi mua 10 quyển vở mỗi quyển giá x đồng và 2 bút bi mỗi chiếc giá y đồng. Biểu
thức đại số biểu thị số tiền bạn Nam phải trả là?
A. 2x - 10y B. 10x - 2y C. 2x + 10y D. 10x + 2y Câu 8: Cho A
∆ BC cân tại A , có B = 52° . Góc A có số đo bằng bao nhiêu độ? A. 100°. B. 72°. C. 96° . D. 76°.
Câu 9: Đa thức nào dưới đây là đa thức một biến? A. 3 2 x – 2x 3 + . B. 2
x + y +1. C. 2
xy + x – 3.
D. xyz – yz + 3.
Câu 10: Hệ số tự do của đa thức 2
P = 2x + 9x 1945 + là: A. 2 B. 9 C. 1945 D. x
Câu 11: Cho tam giác ABC nhọn có AB = AC . Gọi M là trung điểm của BC . Góc BAM bằng góc nào? A. CAM . B. CAB . C. ABM . D. ACB .
Câu 12: Giá trị của biểu thức A = –(2a + b) tại a =1; 3 b = là A. A = 5 − .
B. A = 5. C. A = 1 − . D. A =1.
Câu 13: Cho P = x −1
và Q =1– .xKhi đó khẳng định đúng là: A. P − Q = 0. B. P + Q = 0.
C. Q − P = 0. D. Q + P = 2.
Câu 14: Kết quả phép chia ( 3 4
2x − 3x ): x là A. 2 4 2x −3x . B. 2 3 2x −3x . C. 2 3 2x + 3x . D. 2 4 2x − 3x . Trang 1/2
Câu 15: Bậc của đa thức: 4 3 2
y − 3+ 2y − 3y 2 − y là: A. 3. B. 1. C. 2 . D. 4 .
Câu 16: Cho tam giác ABC cân tại A, biết 0
B = 50 .Tính số đo các góc còn lại của tam giác đó. A. 0 = 0 A 50 ;C = 80 B. 0 = 0 A 80 ;C = 50 C. 0 = 0 A 40 ;C = 90 D. 0 = 0
A 90 ;C = 40 .
Câu 17: Trong các phát biểu sau dữ liệu nào không phải là số liệu?
A. Số học sinh dưới trung bình môn toán.
B. Xếp loại thi đua khen thưởng của học sinh cuối năm.
C. Số học sinh đạt loại giỏi môn toán.
D. Điểm trung bình cuối năm của các môn học.
Câu 18: Sắp xếp đa thức 4 2 3 –x 2
+ − 3x + 5x – x theo lũy thừa tăng dần của biến x ta được: A. 2 3 4
2 – x − 3x + 5x – x . B. 4 3 2
–x + 5x −3x + 2 –x . C. 4 3 2
–x + 5x −3x –x + 2. D. 3 2 4
2 – x + 5x −3x – x .
Câu 19: Cho A(x) 2
= x − 3x + 2 và B(x) = 3x −1. Khi đó A(x) + B(x) bằng: A. 2 x −1 B. 2 x +1 C. 2 x − 6x +1 D. 2 x − 6x + 3
Câu 20: Đa thức f (x) = 2x − 2 có nghiệm là A. x =1 B. x = 2 C. x = 3 D. x= -1
B- TỰ LUẬN (5,0 điểm) Câu 21 (1,0 điểm)
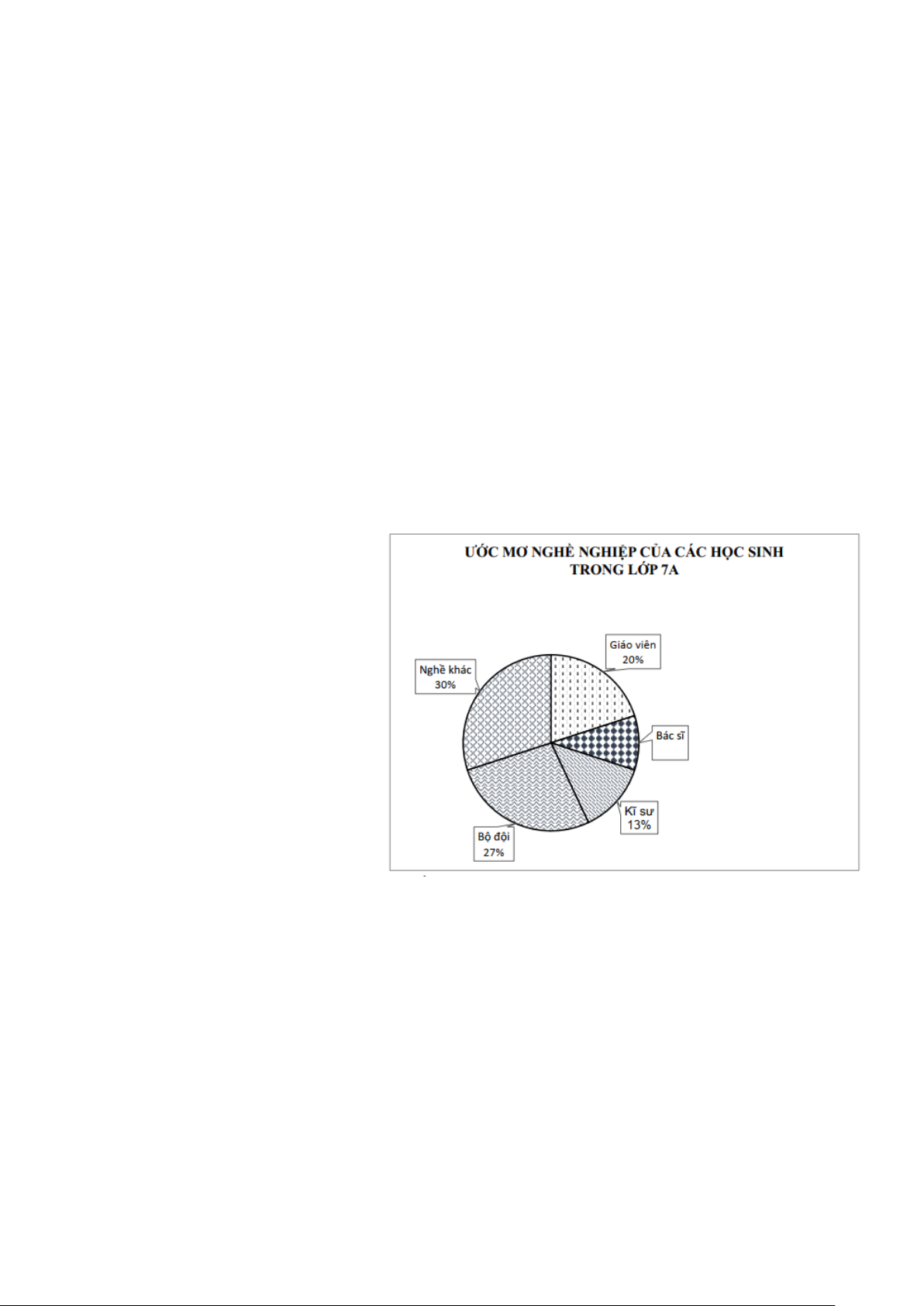
Cho biểu đồ như hình bên:
a) Tính tỉ lệ phần trăm học sinh lớp 7A ước mơ làm bác sĩ ?
b) Tính số học sinh có mơ ước làm
giáo viên biết sĩ số lớp 7A là 40 học sinh. Câu 22 (1,5 điểm).
1) Cho đa thức Q(x) 3 2 2 = 2
− x + x − 4x + 3 − 5x .
a) Thu gọn và sắp xếp đa thức trên theo luỹ thừa giảm dần của biến. Tìm bậc của đa thức.
b) Tính giá trị của đa thức Q(x) khi x = 2 − . 2) Làm tính nhân: 2 x 2
3 . x 2x 1
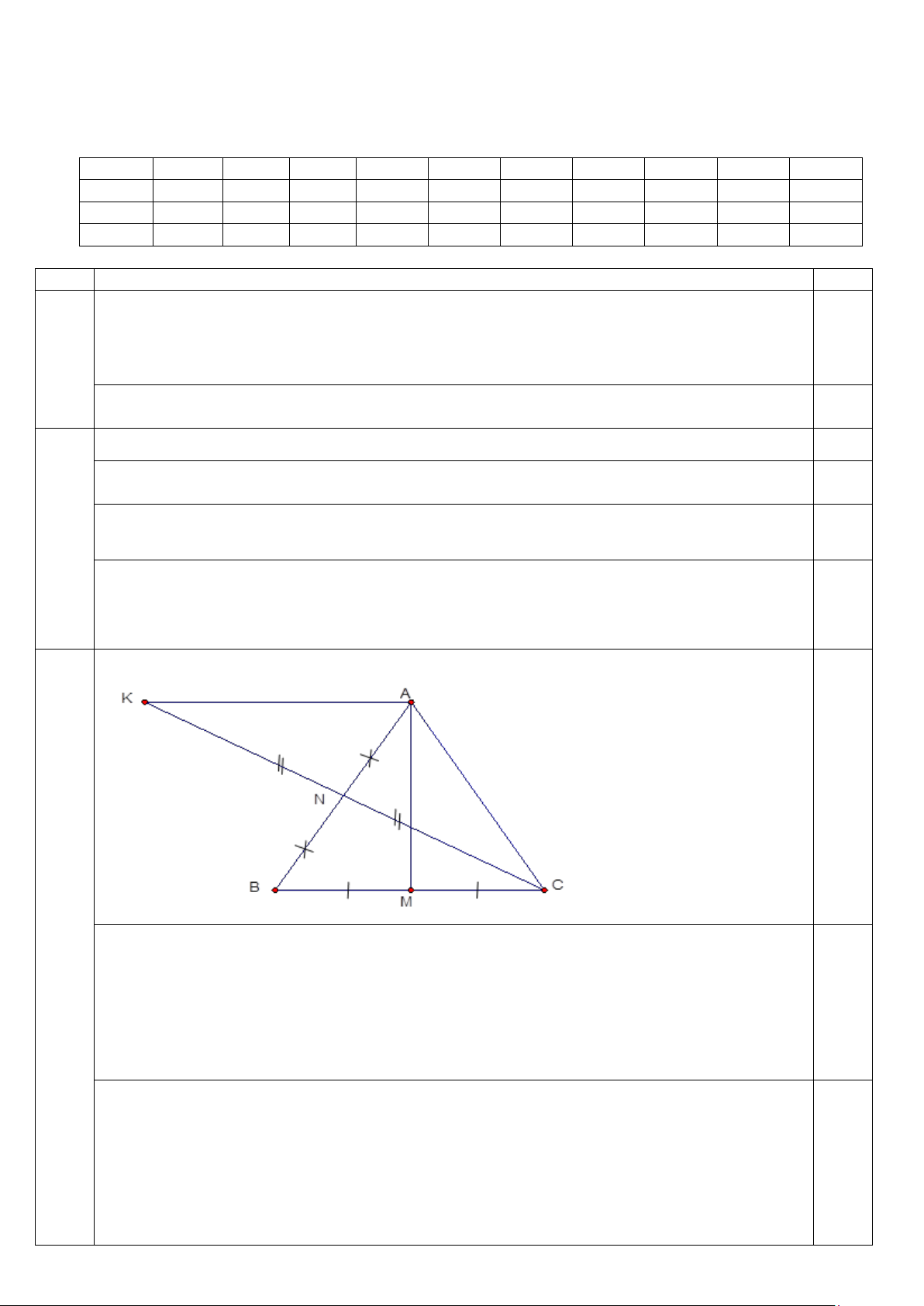
Câu 23 (2,0 điểm): Cho ABC Δ
có AB = AC và M là trung điểm của BC. Gọi N là trung điểm
của AB, trên tia đối của tia NC lấy điểm K sao cho NK = NC.
a) Chứng minh: ∆ABM = ∆ACM
b) Chứng minh rằng: AK = BC từ đó chỉ ra AK = 2MC c) Tính số đo của MAK ?
Câu 24 (0,5 điểm): Cho đa thức: 2
f (x) = ax + bx + c . Biết a, b, c là các số nguyên và 2a + b = 0.
Chứng minh rằng: f (5).f ( 3
− ) là số chính phương.
---------------------- Hết--------------------- Trang 2/2
PHÒNG GD HUYỆN HIỆP HOÀ
ĐÁP ÁN KIỂM TRA GIƯA HỌC KỲ II MÔN: TOÁN - LỚP 7 NĂM HỌC 2023 - 2024
Phần I: Trắc nghiệm khách quan (5.0 đ)
Mỗi câu trả lời đúng 0.25 đ Câu 1 2 3 4 5 6 7 8 9 10 Đ. A C B B B A C D D A C Câu 11 12 13 14 15 16 17 18 19 20 Đ.A A A B B D B B A B A
Phần II: Tự luận (5.0 đ) Câu Nội dung trình bày Điểm Câu
a) Số học sinh ước mơ làm bác sĩ chiếm số phần trăm học sinh cả lớp là: 1
100% − (20% + 30% + 27% +13%) =10% 0.5 (1
điểm) b) Số học sinh thích làm giáo viên là:
20% . 40 = 8 (học sinh) 0.5 1. Q(x) 3 2 2 3 2 = 2
− x + x − 4x + 3− 5x = x − 9x − 2x + 3 0.25 Bậc 3 0.25
Câu 2 Thay x = 2
− vào ta được Q(− ) = (− )3 − (− )2 2 2 9 2 − 2.( 2 − ) + 3 = 37 − 0.25 (1.5 0.25
điểm) KL:….. 2. 2 x 2
3 . x 2x 1 0.25 2 2 2 2
3x .x 3x .2x 3x .(1) 4 3 2
3x 6x 3x 0.25 Câu 3 (2.0 điểm) 0.25 a) 0.75 Xét ∆ABM và ∆ACM có: AB = AC (GT) AM là cạnh chung
MB = MC (Vì M là trung điểm của BC) Vậy ∆ABM = ∆ACM (c-c-c) + Xét ∆ANK và ∆BNC có:
NA = NB (Vì N là trung điểm AB) =
ANK BNC (2 góc đối đỉnh) 0.25 NK = NC (GT)
Suy ra: ∆ANK = ∆BNC (c-g-c)
⇒ AK = BC (2 cạnh tương ứng). (1) 0.25
T ừ (1) và (2) ⇒ AK = 2.MC Trang 3/2
Ta có: ∆ABM = ∆ACM (theo a) ⇒ = AMB AMC 0.25 Mà + 0
AMB AMC =180 (Hai góc kề bù) ⇒ = 0
AMB AMC = 90 ⇒ AM ⊥ BC (1)
Lại có: ∆ANK = ∆BNC (theo b) ⇒ = AKN BCN 0.25 Mà
AKN, BCN nằm ở vị trí so le trong. Do đó: AK // BC (2)
Từ (1) và (2) suy ra: AM ⊥ AK. Vậy MAK = 900 Ta có:
f (5) = 25a + 5b + c f ( 3)
− = 9a − 3b + c
Xét hiệu: f (5) − f ( 3
− ) = (25a + 5b + c) − (9a − 3b + c) 0.25
= 25a + 5b + c − 9a + 3b − c
Câu =16a +8b = 8(2a +b) 4 (0.5 = 8.0 = 0
điểm) ⇒ f = f − ⇒ f f − =[f − ]2 (5) ( 3) (5). ( 3) ( 3) 0.25 Do a, ,
b c∈ Z ⇒ 9a − 3b + c∈ Z ⇒ f ( 3) − ∈ Z ⇒ [ f − ]2
( 3) là số chính phương ⇒ f (5). f ( 3
− ) là số chính phương
Vậy chứng tỏ rằng f (5). f ( 3
− ) là số chính phương Trang 4/2