
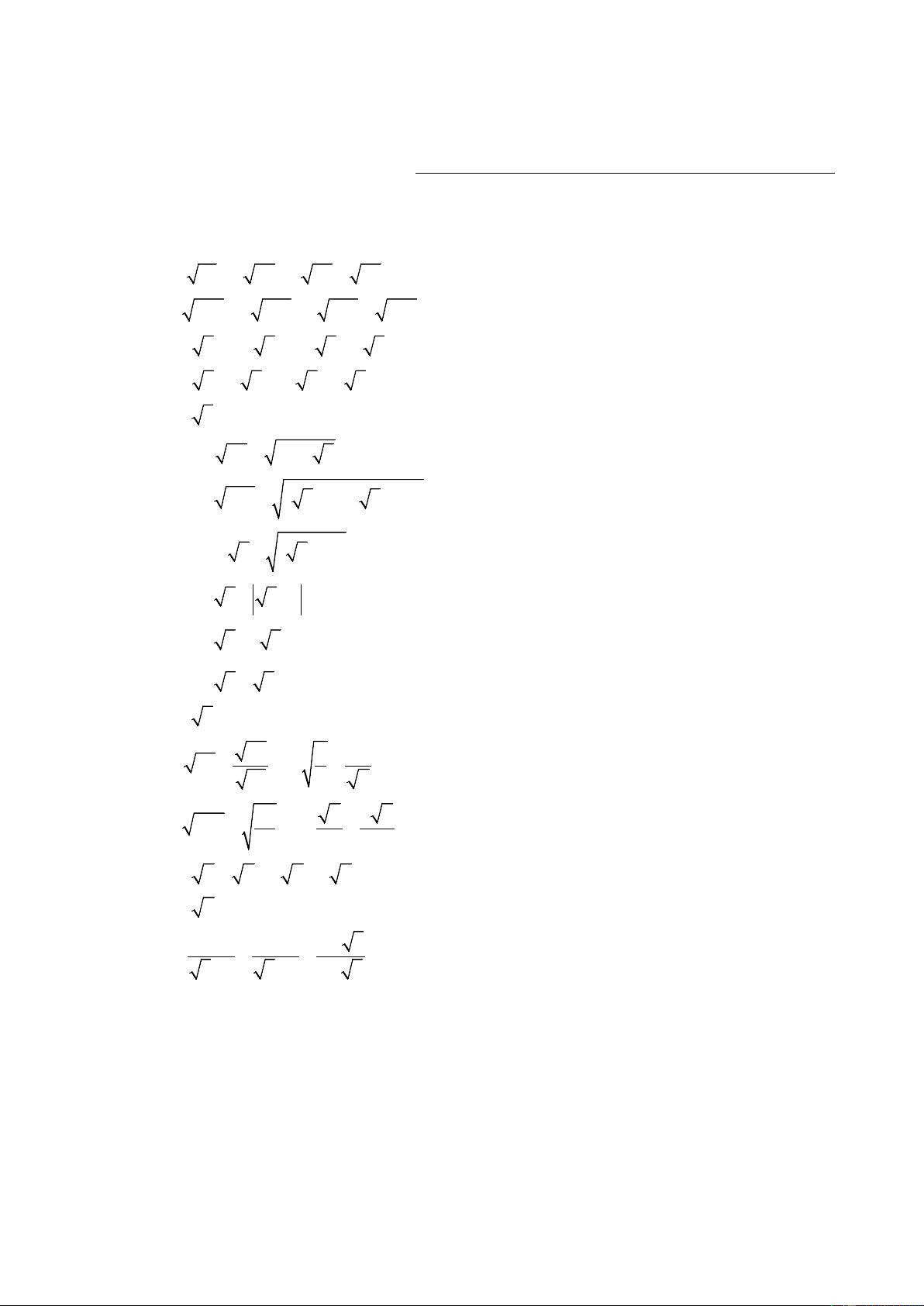
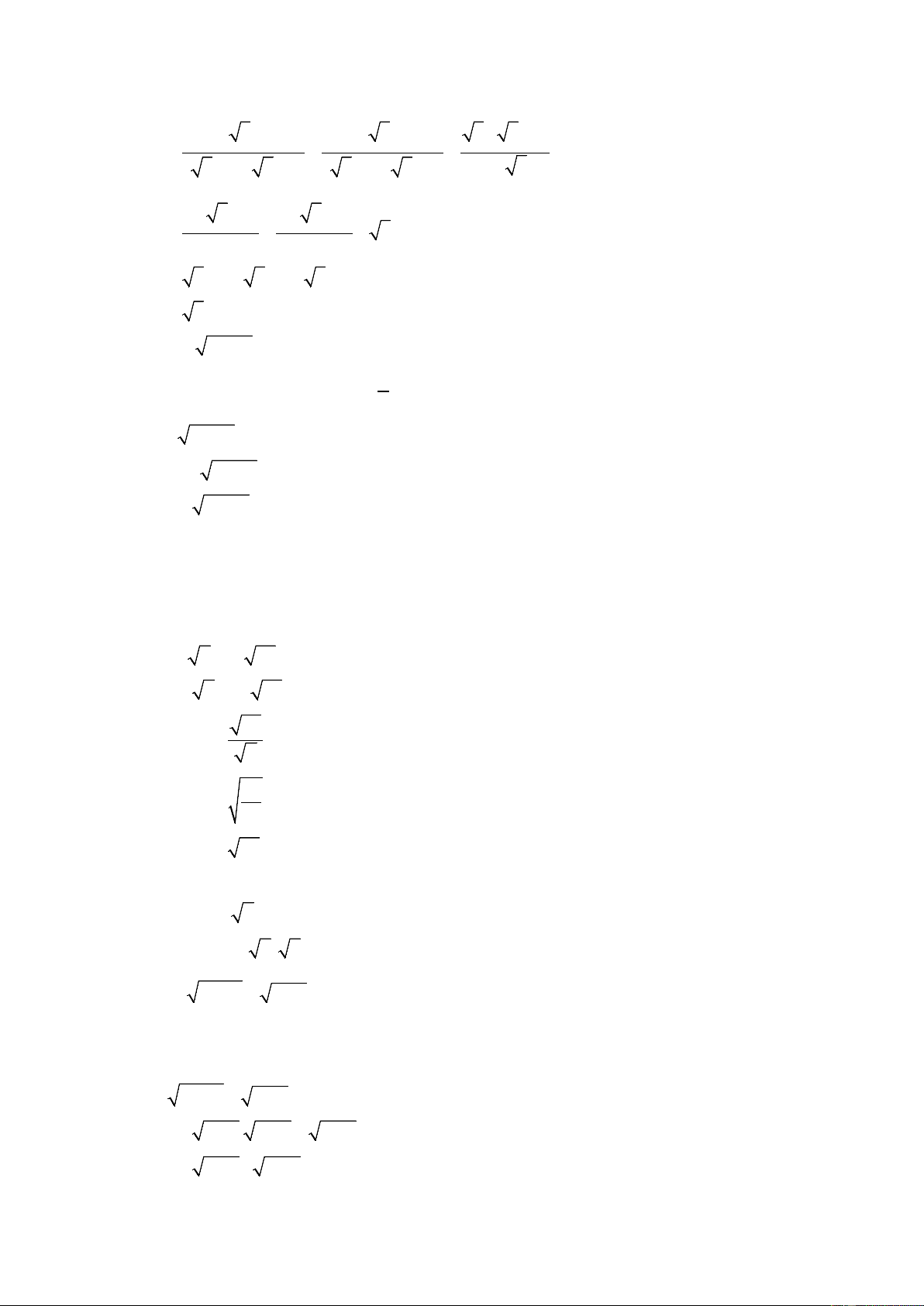

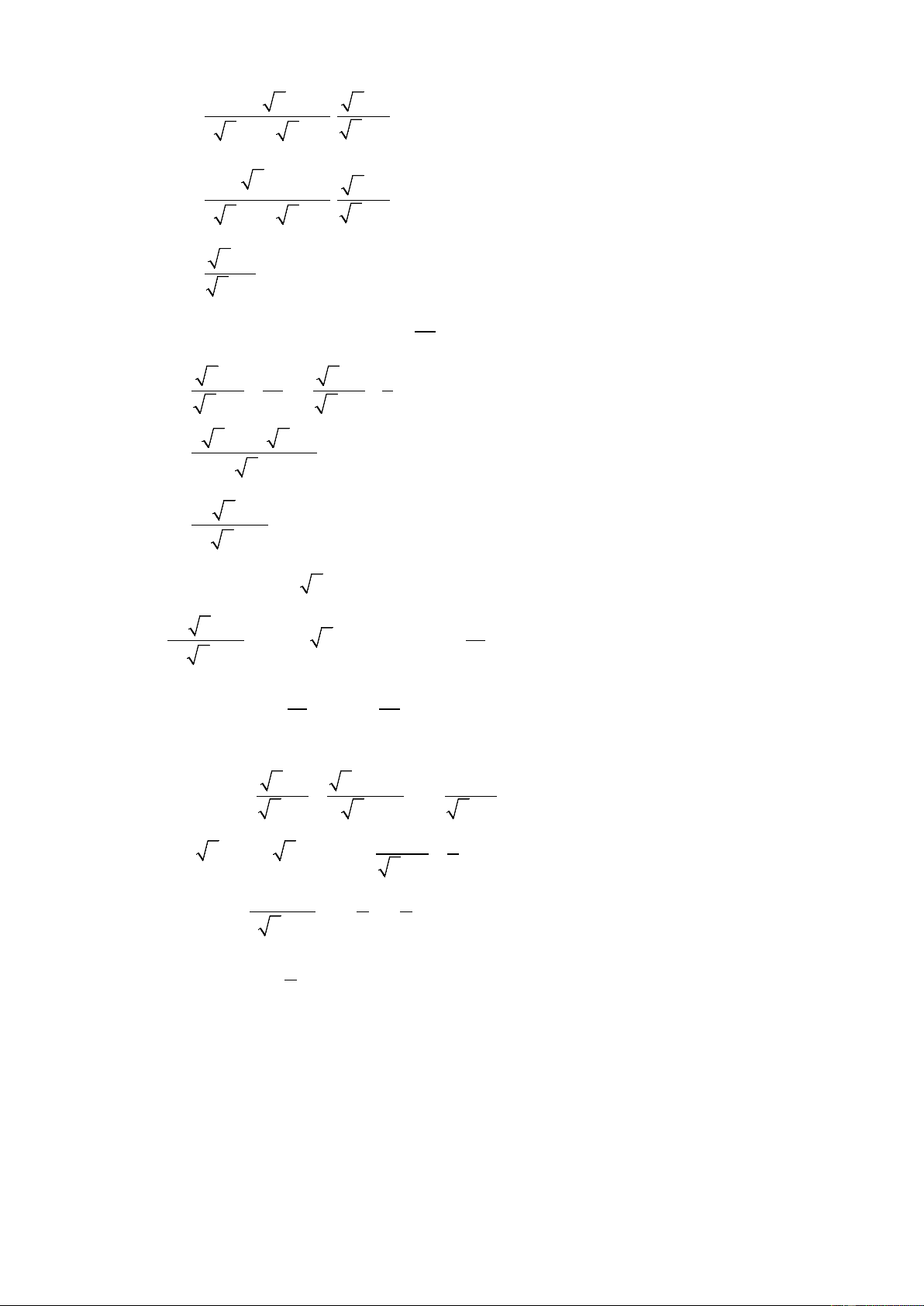

Preview text:
PHÒNG GD VÀ ĐT NAM TỪ LIÊM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS MỄ TRÌ NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Bài 1:
(2 điểm). Thực hiện phép tính
a) 12 − 2 27 + 3 75 − 48 . b) 1+ 2 27 − 4 + 2 3 . 62 1 6 2 2 3 − 3 c) 32 + −12 + . d) + + . 31 2 2 3 −1 3 +1 1− 3 Bài 2:
(2 điểm). Tìm x biết
a) 3 2x − 3 − 6 = 9 . b) 2 2x − 98 = 0 . c) 2 x − 9 + x − 3 = 0 . d) 2 1 x −1 9x − 9 − 16x −16 + 27 = 4 . 3 4 81 Bài 3:
(2,0 điểm). Cho hai biểu thức x 1 2 x x 1 P và Q
x 0; x 1 x 1 1 x x 1 x 2
a) Tính giá trị của Q tại x 7 4 3 . b) Rút gọn M . P Q .
c) Tính các giá trị của x để 1 M . 3
d) Tìm giá trị nhỏ nhất của M . Bài 4: (3,5 điểm)
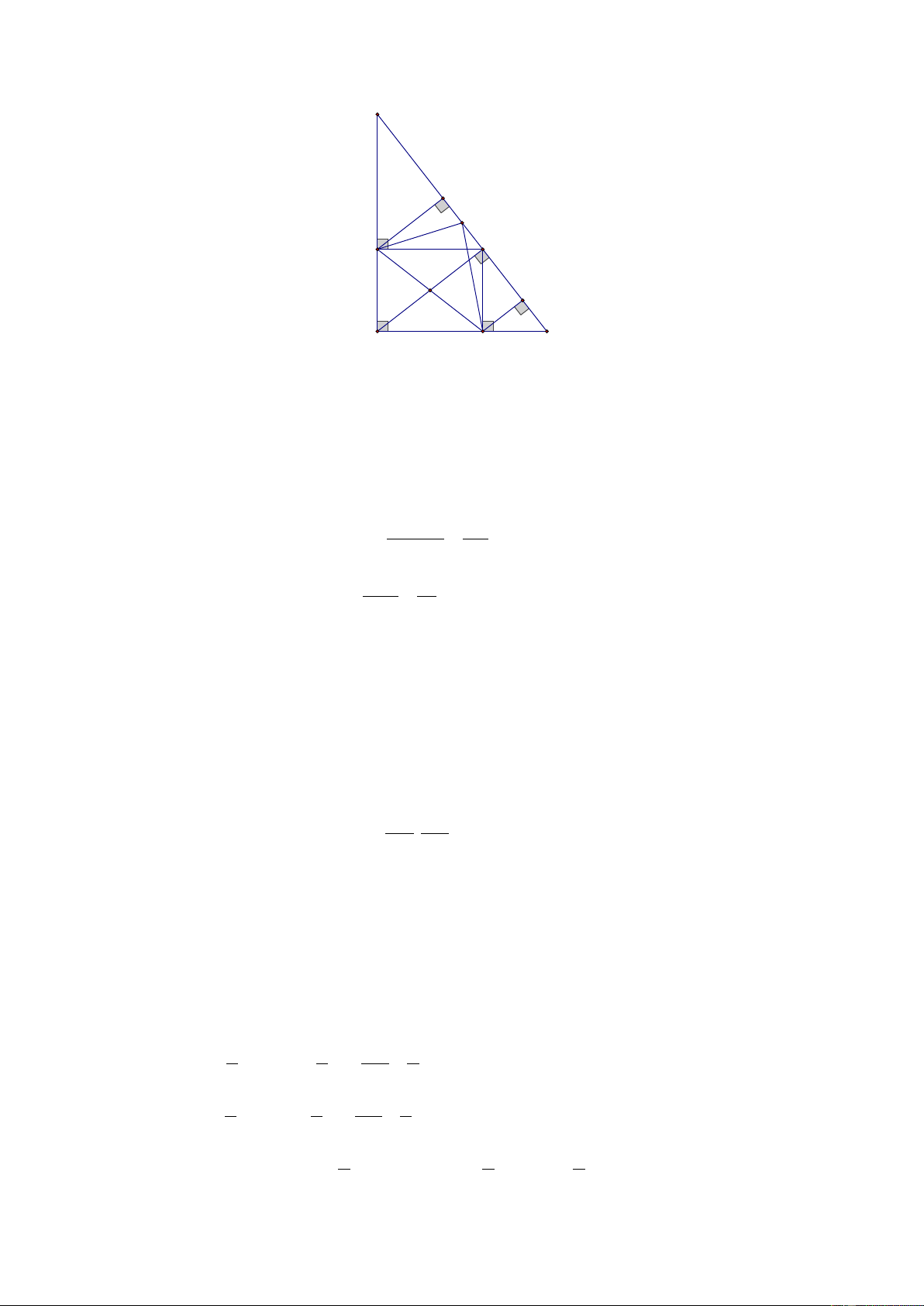
1) Cho tam giác ABC vuông tại A có AB = 6 cm; AC = 8cm . Vẽ AH vuông góc BC tại H .
a) Tính AH , HB, HC .
b) Gọi E, F lần lượt là hình chiếu của H trên AB và AC . Gọi O là giao điểm của AH
và EF . Chứng minh 4 điểm ,
A E, F , H cùng thuộc một đường tròn và .
HB HC = 4.OE.OF . 1
c) Gọi M là trung điểm BC . Chứng minh S = S . AEMF 2 ABC
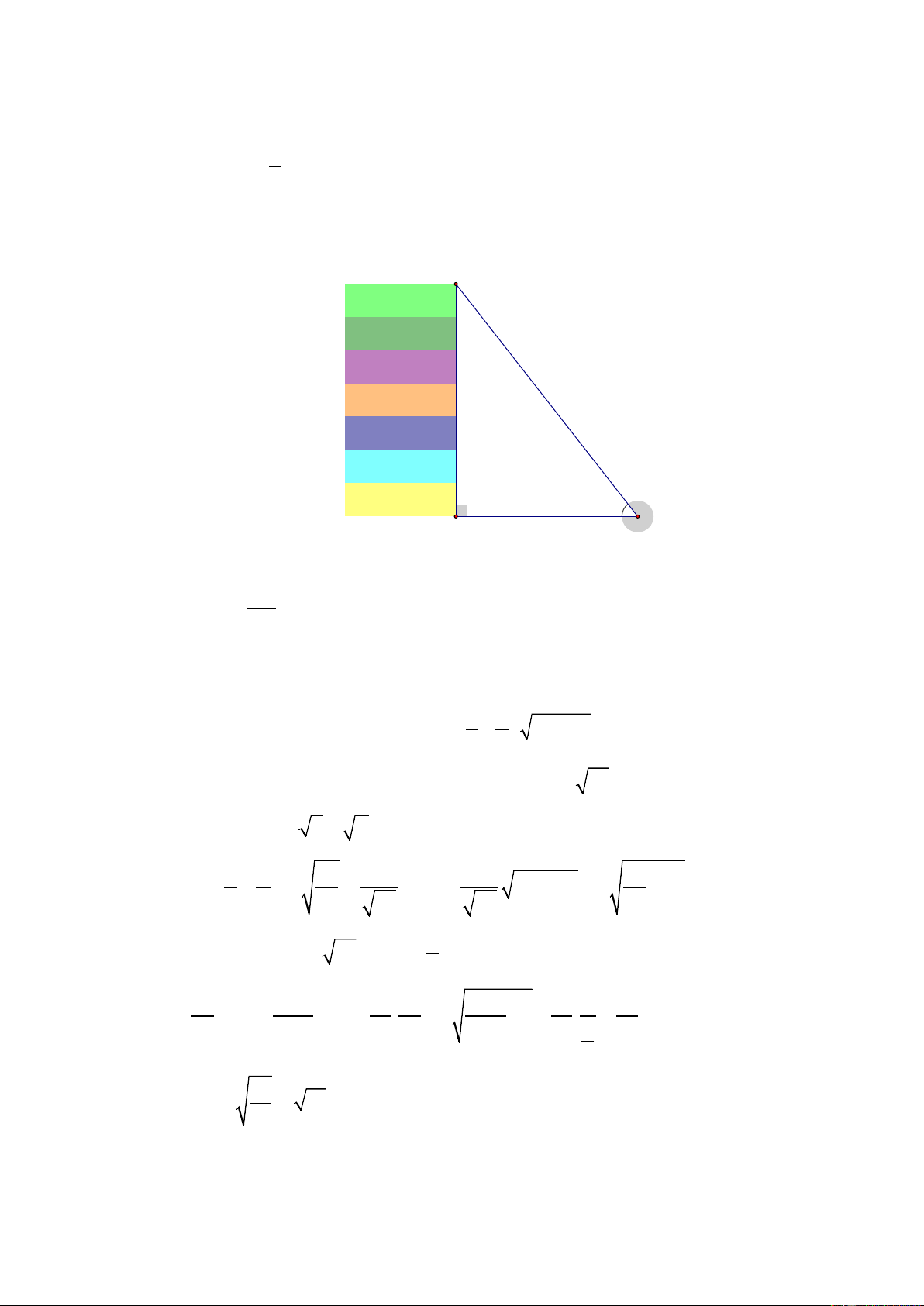
2) Một tòa nhà có chiều cao h (m) . Khi tia nắng tạo với mặt đất một góc 55° thì bóng
của tòa nhà trên mặt đất dài 15 m . Tính chiều cao h của tòa nhà. ( Làm tròn đến chữ số thập phân thứ hai) Bài 5:
(0,5 điểm) Với các số thực dương x, y thỏa mãn x + y ≤ 1. 1 1
Tìm giá trị nhỏ nhất của biểu thức 2 2 P = + 1+ x y . x y HẾT
PHÒNG GD VÀ ĐT NAM TỪ LIÊM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS MỄ TRÌ NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1. a) 12 − 2 27 + 3 75 − 48 2 2 2 2
= 2 .3 − 2 3 .3 + 3 5 .3 − 4 .3
= 2 3 − 2.3 3 + 3.5 3 − 4 3 = 2 3 − 6 3 +15 3 − 4 3 = 7 3 b)1+ 2 27 − 4 + 2 3 = + − ( )2 2 2 1 2 3 .3 3 + 2. 3.1+1 = + − ( + )2 1 2.3 3 3 1 = 1+ 6 3 − 3 +1 = 1+ 6 3 − ( 3 + ) 1 =1+ 6 3 − 3 −1 = 5 3 62 1 6 c) 32 + −12 + 31 2 2 62 2 6 2 2 = 4 .2 + −12. + 31 2 2 = 4 2 + 2 − 6 2 + 3 2 = 2 2 2 2 3 − 3 d) + + 3 −1 3 +1 1− 3 2.( 3 + ) 1 2.( 3 − ) 1 3.( 3 − ) 1 = ( + + 3 − ) 1 ( 3 + ) 1 ( 3− )1( 3+ )1 1− 3 2.( 3 + ) 1 2.( 3 − ) 1 = + − 3 2 2 = 3 +1+ 3 −1− 3 = 3 Câu 2.
a) 3 2x − 3 − 6 = 9 Điề 3
u kiện: 2x − 3 ≥ 0 ⇔ x ≥ 2 3 2x − 3 − 6 = 9 ⇔ 3 2x − 3 =15 ⇔ 2x − 3 = 5 ⇔ 2x − 3 = 25 ⇔ 2x = 28 ⇔ x = 14(TM )
Vậy x = 14 là nghiệm của phương trình. b) 2 2x − 98 = 0 2 ⇔ 2x = 98 98 2 ⇔ x = 2 98 2 ⇔ x = 2 2 ⇔ x = 49 2 ⇔ x = 7 ⇔ x = ± 7
Vậy x ∈{− 7; 7} là nghiệm của phương trình. c) 2 x − 9 + x − 3 = 0 2 − ≥ Điề x 9 0 u kiện: ⇔ x ≥ 3 x − 3 ≥ 0 2 x − 9 + x − 3 = 0
⇔ x − 3. x + 3 + x − 3 = 0
⇔ x − 3.( x +3 + ) 1 = 0
⇔ x − 3 = 0 (do: x +3 +1>1> 0; x ∀ ≥ 3) ⇔ x − 3 = 0 ⇔ x = 3(TM )
Vậy x = 3 là nghiệm của phương trình. 2 1 x −1 d) 9x − 9 − 16x −16 + 27 = 4 3 4 81 Điều kiện: x ≥1 2 1 x −1 9x − 9 − 16x −16 + 27 = 4 3 4 81 2 ( − ⇔ x − ) 1 − (x − ) x 1 9 1 16 1 + 27 = 4 3 4 81 2 1 x −1
⇔ .3. x −1 − .4 x −1 + 27. = 4 3 4 9
⇔ 2 x −1 − x −1 + 3 x −1 = 4 ⇔ 4 x −1 = 4 ⇔ x −1 =1 ⇔ x −1 =1 ⇔ x = 2(TM )
Vậy x = 2 là nghiệm của phương trình. Câu 3. a) Thay x = − = ( − )2 7 4 3 2 3
⇒ x = 2 − 3 (thỏa mãn) vào Q ta được − + − (3− 3)(4+ 3 2 3 1 3 3 ) 9− 3 Q = = = = . 2 − 3 + 2 4 − 3 (4− 3)(4+ 3) 13 b) Rút gọn M = . P Q x 1 2 x x +1 M = − − .
, với x ≥ 0; x ≠ 1 x +1 1− x x −1 x + 2 x 1 2 x x +1 M = + − x + x − ( x + )1( x − ) . 1 1 1 x + 2 x ( x − ) 1 x +1 2 x x +1 M ( = + − x + ) 1 ( x − ) 1
( x + )1( x − )1 ( x + )1( x − ) . 1 x + 2 x − x + x +1− 2 x x +1 M =
( x + )1( x − ) . 1 x + 2 x − 2 x +1 x +1
M = ( x + )1( x − ). 1 x + 2 ( x − )2 1 x +1
M = ( x + )1( x − ). 1 x + 2 x −1 M = . x + 2 −
c) Tính các giá trị của x để 1 M < 3 x −1 1 − − ⇔ < x 1 1 ⇔ + < 0 x + 2 3 x + 2 3 3 x − 3 + x + 2 ⇔ ( < x + ) 0 3 2 4 x −1 ⇔ (
< (x ≥ 0; x ≠ ) 1 x + ) 0 3 2
Theo ĐK ta có 3( x + 2) > 0 4 x −1 1 < ⇔ x − < ⇔ ≤ x < . 3( x + 2) 0 4 1 0 0 16 1 1 −
Vậy với 0 ≤ x < thì M < 16 3
d) Tìm giá trị nhỏ nhất của M x −1 x + 2 − 3 3 Ta có: M = = =1− x + 2 x + 2 x + 2 3 3 Vì: x ≥ 0 ⇒ x + 2 ≥ 2 ⇒ ≤ x + 2 2 3 3 1 ⇒ M =1− ( ≥ − = − . x + 2) 1 2 2 1
Vậy min M = − khi x = 0 . 2 Câu 4. C K M F H Q O A E B 1)
a) Tính AH , HB, HC .
Áp dụng định lý Pytago cho tam giác vuông ABC ta có: 2 2 2 2 2
BC = AB + AC = 6 + 8 = 100 ⇒ BC = 10 cm .
Áp dụng hệ thức lượng cho tam giác vuông ABC ta có: A . B AC 6.8 + A .
B AC = AH .BC ⇒ AH = = = 4,8 cm . BC 10 2 2 AB 6 + 2
AB = BH.BC ⇒ BH = = = 3,6 cm BC 10
Suy ra HC = BC − BH = 10 − 3, 6 = 6, 4 cm . b) Chứng minh ,
A E, F , H cùng thuộc đường tròn:
Xét tứ giác AEFH có = = FAE AEH
AFH = 90° ( giả thiết)
Suy ra tứ giác AEFH là hình chữ nhật nên OA = OF = OE = OH suy ra 4 điểm ,
A E, F , H cùng nằm trên đường tròn tâm O đường kính AH . + Chứng minh .
HB HC = 4.OE.OF EF EF Vì 2
OE = OF ⇒ 4OE.OF = 4. . = EF . 2 2
Mà EF = AH ( vì AEFH là hình chữ nhật) và 2 AH = .
HB HC ( hệ thức lượng trong tam giác vuông) nên .
HB HC = 4.OE.OF .
c) Kẻ FK ⊥ BC tại K , EQ ⊥ BC tại Q .
Suy ra FKQE là hình thang vuông.d Vì O là trung điểm EF mà OH / /EQ ( cùng ⊥ BC )
Suy ra OH là đường trung bình của hình thang FKQE ⇒ EQ + FK = 2OH = AH . 1 1 BC 1 S
= FK.MC = FK. = FK.BC F ∆ MC 2 2 2 4 1 1 BC 1 S = E . Q MB = E . Q = E . Q BC E ∆ MB 2 2 2 4 1 1 1 Suy ra S + S
= BC FK + EQ = BC AH = S FM ∆ C EM ∆ B ( ) . ∆ 4 4 2 ABC 1 1 Mà: S + S + S = S ⇒ S + S = S ⇒ S = S AEMF EM ∆ B FM ∆ C ABC AEMF ∆ ∆ 2 ABC ABC AEMF 2 ABC 1 Vậy: S = S . AEMF 2 ABC
2) Gọi chiều cao của tòa nhà là h = AC , bóng của tòa nhà lên mặt đất là AB = 15 m , góc
tạo bởi tia nắng với mặt đất là
CBA = 55° ( như hình vẽ) C h (m) 550 A B 15m
Áp dụng tỉ số lượng giác của góc nhọn cho tam giác vuông ABC ta có: AC = ⇒ = tan CBA AC A .
B tan CBA = 15. tan 55° ≈ 21, 42 m AB
Vậy tòa nhà cao 21, 42 m . Câu 5.
Với các số thực dương x, y thỏa mãn x + y ≤ 1. 1 1
Tìm giá trị nhỏ nhất của biểu thức 2 2 P = + 1+ x y . x y
Với x, y là hai số thực không âm nên ta có: x + y ≥ 2 xy ( )1
Thật vậy ( ) ⇔ ( x − y )2 1 ≥ 0 luôn đúng 1 1 1 2 2 1 Ta có : 2 2 + ≥ 2 = ⇒ P ≥ 1+ x y ≥ 2 + xy . x y xy xy xy xy 1
Ta có : 1 ≥ x + y ≥ 2 xy ⇒ xy ≤ . 4 1 1 15 1 1 15 1 17 ⇒ + xy = + xy + . ≥ 2 .xy + . = xy 16xy 16 xy 16xy 16 1 4 4 17 ⇒ P ≥ 2 = 17 . 4 x = y 1
Vậy giá trị nhỏ nhất của P là 17 . Dấu bằng xảy ra khi x + y = 1 ⇔ x = y = . 2 1 xy = 4 HẾT




