Đề thi giữa kì 1 Toán 9 năm 2020 – 2021 trường THCS Nguyễn Quý Đức – Hà Nội

Nhằm kiểm tra đánh giá chất lượng dạy và học môn Toán lớp 9 định kỳ, ngày … tháng 11 năm 2020, trường THCS Nguyễn Quý Đức, quận Nam Từ Liêm, thành phố Hà Nội tổ chức kỳ thi kiểm tra chất lượng giữa học kỳ 1 môn Toán 9 năm học 2020 – 2021.Mời bạn đọc đón xem.

52 26 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK1 Toán 9

Môn: Toán 9

Thông tin:

6 trang 9 tháng trước

Tác giả:

Profile Hà Việt Anh
b
a
E
A
60
°
PHÒNG GD VÀ ĐT NAM TỪ LIÊM
T
RƯỜNG THCS NGUYỄN QUÝ ĐỨC
----------
THCS.TOANMATH.com
Câu 1: Thực hiện phép tính:
a)
0,2. 500
b)
20 80 45
c)
d)
10 5 3 5 5 2
21 53 2



Câu 2: Giải phương trình:
a)
3 18x 
b)
2
69 2xx 
c)
11
2 9 3 25 3 49 3 20
57
xxx
d)
2 2 19 1xx 
Câu 3: Cho 2 biểu thức:
2
1
x
A
x
và
586
1
11
xx
B
x
xx


với
0, 1xx
a) Tính giá trị của A khi
9x
b) Rút gọn
B
c) Tìm các giá trị của x để
.
2
x
AB
.
Câu 4:
1) Một con thuyền ở điểm
A
di chuyển từ bờ sông a
sang bờ sông b với vận tốc trung bình là 5km/h
vượt qua khúc sông nước chảy mạnh trong 15 phút.
Biết đường đi của con thuyền là AE.
Tính chiều rộng khúc sông.
2) Cho
ABC
vuông tại B, đường cao BH, biết AB =
9cm, AC = 15cm.
a) Giải tam giác vuông ABC
b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh tứ giác BEHF là hình
chữ nhật và tính độ dài EF.
c) Tính
..BE EA BF FC
và chứng minh
3
BEHF
BH
S
AC
Câu 5: Cho
3
số dương
a
,
b
,
c
Chứng minh rằng
222
222
a b c abc
b c a bca

__________ THCS.TOANMATH.com __________
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
NĂM HỌC 2020 - 2021
MÔN TOÁN - LỚP 9
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
HƯỚNG DẪN GIẢI CHI TIẾT
Câu 1:
a)
0,2. 500
0,2.500
100
10
b)
20 80 45
4.5 16.5 9.5
25 45 35
35
c)
23 3
2 9.3 3 2
33
 
33
63 2 3
3

(do
320
)
3 63 2 3 
2 63
d)
10 5 3 5 5 2
21 53 2



5 2 1 53 5
2
21 53



552
2
Câu 2:
a)
3 18x 
(điều kiện
0x
)
3 81x 
39x
9:3x
3x
9x tm
Vậy
9S
b)
2
69 2xx 
(điều kiện:
x
)
2
32x 
32x
TH1:
32x
5x
(nhận)
TH2:
32x 
1x
(nhận)
Vậy
1;5S
c)
11
2 9 3 25 3 49 3 20
57
xxx
(ĐK:
3x
)
11
6 3 .5 3 .7 3 20
57
xxx 
6 3 3 3 20xxx 
6 3 20x 
10
3
3
x 
100
3
9
x
100
3
9
x
127
3
x
(nhận)
Vậy
127
3
S







d)
2 2 19 1xx 
(điều kiện:
19
2
x
)
2 19 2 19 20xx 
2
2 19 2 19 20 0 *xx 
Đặt
2 19tx
(điều kiện:
0t
)
2
(*) 20 0tt 
2
5 4 20 0t tt
54 5 0tt t 

5 40tt
50
40
t
t


5
4
t
t
loaïi
nhaän

2 19 4x 
2 19 16x 
23x 
3
2
x

(nhận)
Vậy
3
2
S







Câu 3:
a) Với
9x
(TM ĐK), thay vào A ta có:
92 32 5
31 2
91
A


Vậy
5
2
A
khi
9x
.
b)

15 1 8 6
11
xx x x
B
xx


5 58 6
11
xx x x
B
xx



21
11
xx
B
xx



2
1
11
x
B
xx


1
1
x
B
x

c) Ta có:
21 2
..
11 1
xx x
AB
xx x



2
.
22
1
xx x
AB
x

24x xx 
40xx 
1 15
0
44
xx



2
1 15
24
x



15 1
2
15 1
2
x
x
nhaän
loaïi

H
b
a
E
A
60
°
b
a
E
A
60
°
16 2 15 8 15
42
x


Câu 4:
1) - Đổi: 15 phút =
1
4
giờ
- Kẻ
EH a H a
- Chiều dài đoạn
AE
là:
15
5. 1,25
44

km
- Xét
AHE
vuông tại
H
có:
0
sin 60 .EH AE
3
.1, 25 1, 08
2

km
Vậy chiều rộng khúc sông là 1,08(km).
2)
a) Xét
ABC
vuông tại
B
có:
2 22
BC AC AB
22
15 9 144 
12BC
cm
Ta có:
12 4
sin 53
15 5
BC
AA
AC

Ta có:
90 37AC C
b) Xét tứ giác BEHF có:
90EBF HEB HFB
nên tứ giác
BEHF
là hình chữ
nhật.
Khi đó:
AH EF
(tính chất hình chữ nhật)
Xét
ABC
vuông tại
B
đường cao BH có:
. .2
ABC
BH AC AB BC S

Suy ra:
.AB BC
BH
AC
9.12
7,2
15

(cm)
Vậy
7,2EF
(cm)
c) Xét
ABH
vuông tại
H
đường cao
HE
có:
2
.BE EA EH
Xét
BHC
vuông tại
H
đường cao
HF
có:
2
.BF FC FH
Suy ra:
2
222
. . 7,2 51,84BE EA BF FC EH FH EF 
(cm)
Ta có:
22 3
... .
.
..
BEHF
BE BA BF BC BH BH BH
S BE BF
BH AC BH AC AC

Câu 5:
Áp dụng bất đẳng thức Cô si, ta có:
2 2 22
2 2 22
2. 2
a b ab a
b c bc c

2 2 22
2 2 22
2. 2
b c bc b
c a ca a

2 2 22
2 2 22
2. 2
c a ca c
a b ab b

Cộng theo vế ta được:
222
222
22
a b c acb
b c a cba






222
222
a b c acb
b c a cba

Đẳng thức xảy ra
abc
__________ THCS.TOANMATH.com __________
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD VÀ ĐT NAM TỪ LIÊM
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1
TRƯỜNG THCS NGUYỄN QUÝ ĐỨC NĂM HỌC 2020 - 2021 MÔN TOÁN - LỚP 9 ----------
Thời gian làm bài: 90 phút (không kể thời gian giao đề) THCS.TOANMATH.com Câu 1: Thực hiện phép tính: a) 0, 2. 500 b) 20  80  45 10  5 3 5  5 2 c)      2 2 1 2 27 3 2 d)   3 3 2 1 5  3 2 Câu 2: Giải phương trình: a) 3 x 1  8 b) 2
x  6x  9  2 1 1 c) 2 9x   3  25x   3  49x   3  20
d) 2x  2x 19  1 5 7 Câu 3: Cho 2 biểu thức: x  2 x 5 8 x  6 A  và B   
với x  0, x 1 x 1 x 1 x 1 x 1
a) Tính giá trị của A khi x  9 b) Rút gọn B x
c) Tìm các giá trị của x để . A B  . 2 Câu 4:
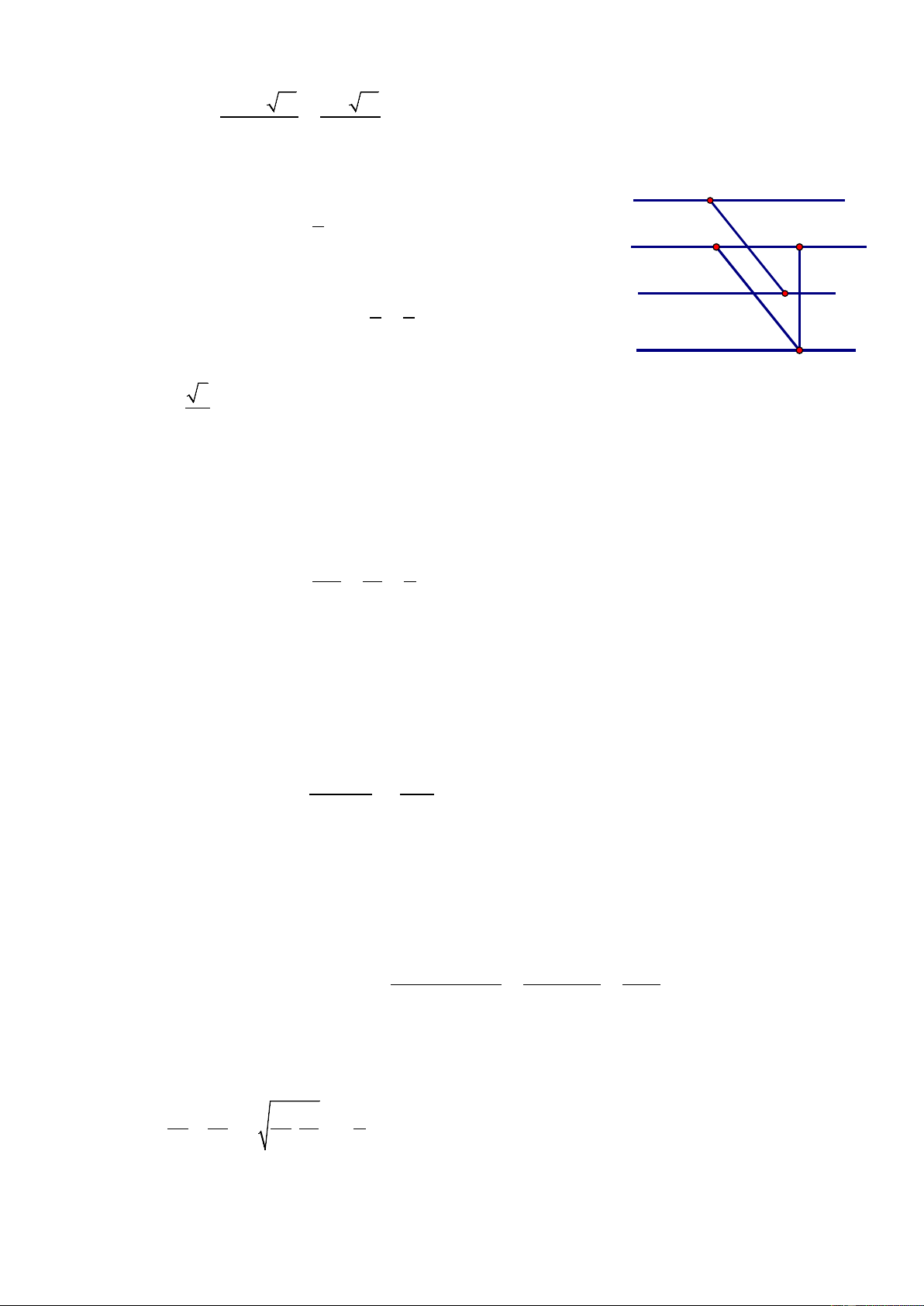
1) Một con thuyền ở điểm A di chuyển từ bờ sông a a A 60°
sang bờ sông b với vận tốc trung bình là 5km/h
vượt qua khúc sông nước chảy mạnh trong 15 phút.
Biết đường đi của con thuyền là AE. b
Tính chiều rộng khúc sông. E 2) Cho A
BC vuông tại B, đường cao BH, biết AB = 9cm, AC = 15cm. a) Giải tam giác vuông ABC
b) Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh tứ giác BEHF là hình
chữ nhật và tính độ dài EF. 3 BH
c) Tính BE.EA BF.FC và chứng minh SBEHF AC Câu 5:
Cho 3 số dương a , b , c 2 2 2 a b c a b c Chứng minh rằng      2 2 2 b c a b c a
__________ THCS.TOANMATH.com __________
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: a) 0, 2. 500  0, 2.500  100 10 b) 20  80  45  4.5  16.5  9.5  2 5  4 5 3 5  3 5 c)      2 2 1 2 27 3 2 3 3 2 3 3   2 9.3  3 2 3 3 3 3 
6 3  2 3 (do 3 2  0 ) 3  3 6 3  2 3  26 3 10  5 3 5  5 2 d)   2 1 5  3 2 5  2   1 5 3 5    2 2 1 5  3  5  5  2  2 Câu 2:
a) 3 x 1  8 (điều kiện x  0 )  3 x  81
 3 x  9  x  9:3  x  3  x  9 tm Vậy S    9 b) 2
x  6x  9  2 (điều kiện: x   )  x 2 3  2  x3  2 TH1: x 3  2  x  5 (nhận) TH2: x 3  2  x 1 (nhận) Vậy S  1;  5 1 1 c) 2 9x   3  25x   3  49x  
3  20 (ĐK: x  3 ) 5 7 1 1
 6 x3  .5 x3  .7x  3  20 5 7
 6 x3  x3  x3  20  6 x3  20 10  x3  3 100  x 3  9 100  x  3 9 127  x  (nhận) 3 127     Vậy S      3    19
d) 2x  2x 19  1 (điều kiện: x  ) 2  2
2x 19  2x 19  20   2x 19  2x 19 20  0   *
Đặt t  2x 19 (điều kiện: t  0 ) 2
(*)  t t  20  0 2
t 5t 4t 20  0
tt   5  4t   5  0  t   5 t  4  0 t 5  0  t40 
t  5 loaïi   t  4  nhaän   2x 19  4  2x 19 16  2x  3 3  x  (nhận) 2 3   Vậy S      2    Câu 3:
a) Với x  9 (TM ĐK), thay vào A ta có: 9  2 3  2 5 A    9 1 31 2 5 Vậy A  khi x  9 . 2 x x   1  5 x   1 8 x   6 b) B
x  1 x  1
x x  5 x 58 x  6  B
x  1 x  1 x  2 x 1
B   x 1 x 1  x  2 1
B   x 1 x 1 x 1  B x 1 x  2 x 1 x  2 c) Ta có: . A B  .  x 1 x 1 x 1 x x  2 x . A B    2 x 1 2
 2 x  4  x x
xx 4  0  1 15  x   x     0   4 4 2  1 15   x       2 4  15 1  x  nhaän  2    15 1  x  loaïi  2 16  2 15 8  15  x   4 2 Câu 4: a A 60° 1 1) - Đổi: 15 phút = giờ A H a 4 60°
- Kẻ EH a H a b 1 5 E
- Chiều dài đoạn AE là: 5.  1, 25 km 4 4 b - Xét A
HE vuông tại H có: 0
EH  sin 60 . AE E 3 
.1, 25  1, 08 km 2
Vậy chiều rộng khúc sông là 1,08(km). 2) a) Xét A
BC vuông tại B có: 2 2 2
BC AC AB 2 2
15 9 144  BC 12 cmBC 12 4 Ta có:  sin A     A  53 AC 15 5 Ta có:   
A C  90  C  37
b) Xét tứ giác BEHF có:   
EBF HEB HFB  90 nên tứ giác BEHF là hình chữ nhật.
Khi đó: AH EF (tính chất hình chữ nhật) Xét A
BC vuông tại B đường cao BH có: BH.AC A . B BC  2S ABC   A . B BC 9.12 Suy ra: BH    7, 2 (cm) AC 15 Vậy EF  7, 2 (cm) c) Xét A
BH vuông tại H đường cao HE có: 2
BE.EA EH Xét B
HC vuông tại H đường cao HF có: 2
BF.FC FH
Suy ra: BE EA BF FC EH FH EF   2 2 2 2 . . 7, 2  51,84 (cm) 2 2 3 BE.B . A BF.BC BH .BH BH Ta có: SBE.BF    BEHF BH.AC BH.AC AC Câu 5:
Áp dụng bất đẳng thức Cô si, ta có: 2 2 2 2 a b a b a   2 .  2 2 2 2 2 b c b c c 2 2 2 2 b c b c b   2 .  2 2 2 2 2 c a c a a 2 2 2 2 c a c a c   2 .  2 2 2 2 2 a b a b b Cộng theo vế ta được: 2 2 2 a b c  a c b   2    2        2 2 2 b c a     c b a  2 2 2 a b c a c b       2 2 2 b c a c b a
Đẳng thức xảy ra  a b c
__________ THCS.TOANMATH.com __________