THCS TỨ HIỆP
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Câu 1.
(1,5 điểm) Rút gọn các biểu thức sau:
1) 27 − 2 3 + 2 48 − 3 75 . 2) ( − )2 1 5 2 − 20 . 2  10 − 5 6 + 2  1 3)  +  :   . 2 −1 3 +1 5 − 2   Câu 2.
(1,5 điểm) Giải các phương trình sau: 1) x −1 = 2 . 1 1 2) 16x − 32 −
9x −18 + 25x − 50 = 6 . 2 3
3) 3 − x = 2x − 3 . Câu 3.
(2,5 điểm) Cho hai biểu thức x +1 2 x x 3x − 3 Q = và P = + +
với x ≥ 0; x ≠ 9 . x − 3 x − 3 x + 3 9 − x
1) Tính giá trị của Q tại x = 16 . 3 x + 3
2) Chứng minh rằng: P = x − . 9 P
3) Tìm x là số nguyên để M = là số nguyên. Q 4x + 7 4) Cho A = . x M + . Tìm GTNN của A . x + 3 Câu 4.
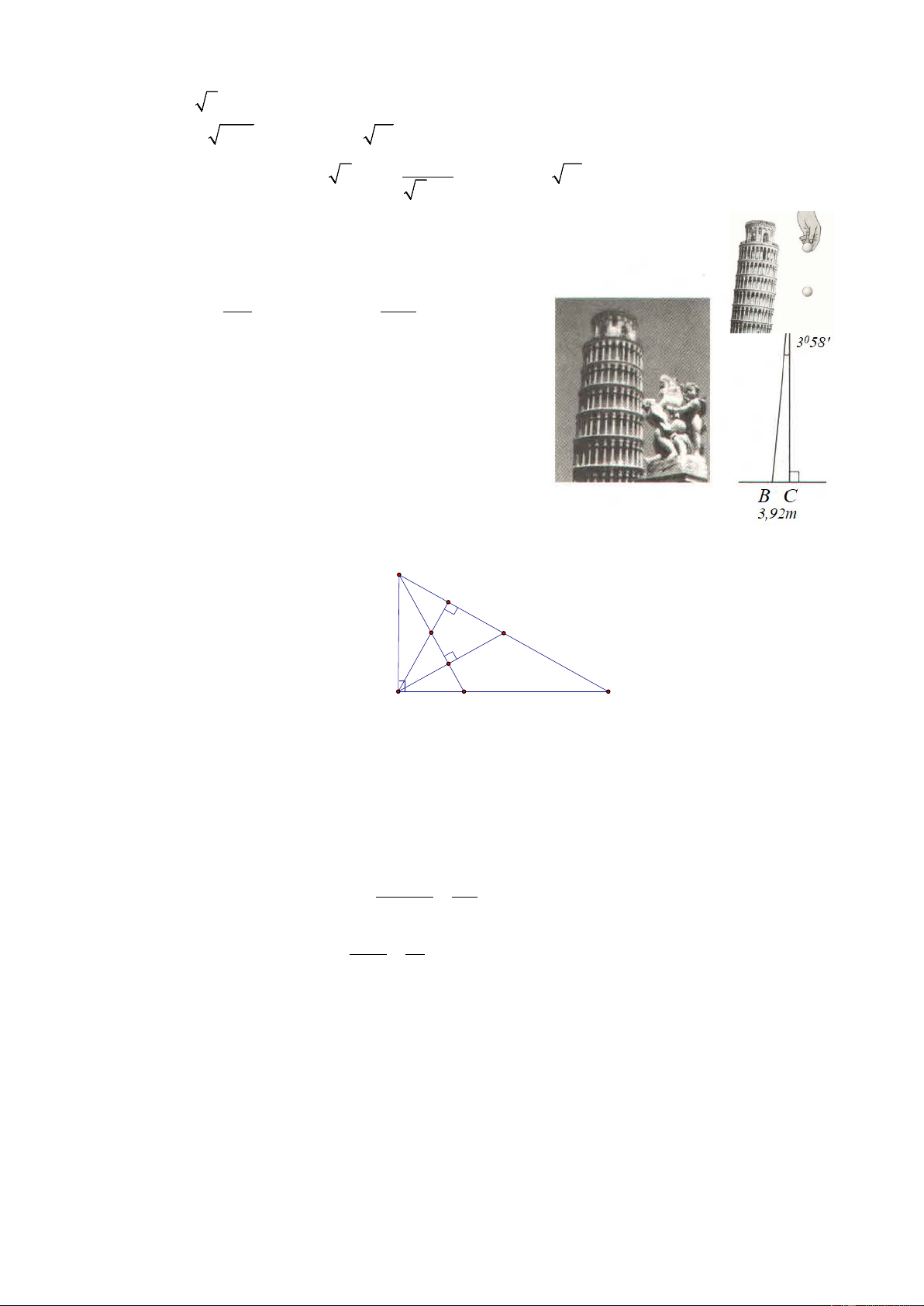
(1,0 điểm) Tháp Pisa ở Ý là một trong những địa điểm du lịch rất nổi
tiếng. Năm 2019 tòa tháp trong 864 tuổi và người ta đo được độ nghiêng
của tháp so với phương thẳng đứng là 3 58
° ' . Khi thả một quả cầu bằng
đá rơi theo phương thẳng đứng từ đỉnh tháp (bỏ qua lực cản không khí,
gió), người ta đo được điểm rơi cách chân tháp 3,92 m. Tính khoảng cách
từ đỉnh tháp đến mặt đất? (Làm tròn đến chữ số thập phân thứ hai). Câu 5.
(3 điểm) Cho tam giác ABC vuông tại A , đường cao AH . Biết AB = 3cm, AC = 4 cm.
1) Tính độ dài BC, AH,CH, BH .
2) Gọi M là trung điểm của BC .Kẻ BE ⊥ AM tại E . BE cắt AH tại D , BE cắt AC
tại F .Chứng minh BE.BF = BH.BC . 2 AB BH 3) Chứng minh : =
và D là trung điểm của BF . 2 AC CH Câu 6.
(0,5 điểm) Giải phương trình: 3 x = x − 7 ( x − 2) + 7 .  HẾT  THCS TỨ HIỆP
ĐỀ KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2020 - 2021 ---------- MÔN TOÁN - LỚP 9 THCS.TOANMATH.com
Thời gian làm bài: 90 phút (không kể thời gian giao đề) Câu 1. 1) 27 − 2 3 + 2 48 − 3 75 2 2 2
= 3 .3 − 2 3 + 2 4 .3 − 3 5 .3 = 3 3 − 2 3 + 8 3 −15 3 = 6 − 3 . 1 2) ( − )2 1 5 2 − 20 2
= 5 − 2 − . 2 .5 = 5 − 2 − 5 = 2 − . 2 2   5 ( 2 − )1 2( 3 + ) 10 − 5 6 + 2  1 1 3)  +  : =  + .( 5 − 2)   2 −1 3 +1 5 − 2    2 −1 3 +1   
= ( 5 + 2)( 5 − 2) = 5− 2 = 3. Câu 2.
1) x −1 = 2 (Điều kiện : x ≥ 1) 2 ⇔ x −1 = 2 ⇔ x −1 = 4
⇔ x = 5 (thỏa mãn).
Vậy phương trình có tập nghiệm S = { } 5 1 1 2) 16x − 32 −
9x −18 + 25x − 50 = 6 2 3
Điều kiện: x ≥ 2 . 1 1 Ta có: 2 4 ( x − 2) 2 − 3 ( x − 2) 2
+ 5 (x − 2) = 6 2 3 1 1
⇔ .4 x − 2 − .3 x − 2 + 5 x − 2 = 6 2 3
⇔ 2 x − 2 − x − 2 + 5 x − 2 = 6
⇔ 6 x − 2 = 6 ⇔ x − 2 = 1 ⇔ x − 2 = 1
⇔ x = 3 (thỏa mãn)
Vậy phương trình có tập nghiệm S = { } 3
3) 3 − x = 2x − 3 . Điều kiện: x ≤ 3 . PT tương đương: 2x − 3 ≥ 0  3  − x =  (2x −3)2  3 x ≥ ⇔  2 2 3
 − x = 4x −12x +9  3 x ≥ ⇔  2 2
4x −11x +6 = 0  3 x ≥  2 
⇔ x = 2 ⇔ x = 2 ( Thỏa mãn điều kiện)  3 x =  4
Vậy phương trình có tập nghiệm S = { } 2 . Câu 3. 16 +1 5
1) Thay x = 16 (TMĐK) vào biểu thức Q , ta có: Q = = = 5. 16 − 3 1
Vậy Q = 5 tại x = 16 . 2 x x 3x − 3 2) P = + +
với x ≥ 0; x ≠ 9 x − 3 x + 3 9 − x
2 x ( x + 3) + x ( x − 3) − 3x + 3 P = ( x +3)( x −3) 3 x + 3
P = ( x +3)( x −3) 3 x + 3 P = x − . 9 3 + + ( x + P x x )1 3 3 1 x − 3 3 3) Ta có: M = = : = = Q x − x −
( x −3)( x +3). 9 3 x +1 x + 3
Với mọi x thỏa mãn ĐKXĐ: 3 x ≥ 0 ⇒ x + 3 ≥ 3 ⇒ ≤1 x + 3
Ta có: 0 < M ≤ 1 mà M nguyên nên M = 1 3 Suy ra:
=1 ⇔ x = 0 (thỏa mãn điều kiện) x + 3
Vậy x = 0 thì M nhận giá trị nguyên. 4x + 7 4) A = . x M + x + 3 3 4x + 7 7x + 7 70 A = x + = = x − + = ( x + ) 70 . 7 21 7 3 + − 42 x + 3 x + 3 x + 3 x + 3 x + 3
Do x + 3 > 0 với mọi x ≥ 0; x ≠ 9 nên Áp dụng BĐT Cauchy, ta có:
A ≥ 2 7.70 − 42 ⇒ A ≥ 14 10 − 42
Dấu “=” xảy ra ⇔ ( x + ) 70 7 3 =
⇔ x = 19 − 6 10 . x + 3 Câu 4.
Ta có mô tả như hình vẽ bên. Xét A
∆ BC vuông tại C có: BC 3, 92 sin A = Hay sin 3 58 ° ' = AB AB
Suy ra: AB = 56, 67
Vậy khoảng cách từ đỉnh tháp tới mặt đất là 56, 67 m. Câu 5. ( B H M D E A F C 1) Xét A
∆ BC vuông tại A .
Áp dụng định lí pytago vào tam giác vuông ta có: 2 2 2
BC = AB + AC = 9 +16 = 25 ⇒ BC = 5 cm . Xét A
∆ BC vuông tại A ; đường cao AH
Áp dụng hệ thức lượng trong tam giác vuông ta có: A . B AC 3.4
AH .BC = A . B AC ⇒ AH = = = 2, 4cm . BC 5 2 AC 16 2
AC = HC.BC ⇒ HC = = = 3, 2cm BC 5
⇒ HB = BC − HC = 5 − 3, 2 = 1,8cm .
2) Gọi M là trung điểm của BC .Kẻ BE ⊥ AM tại E . BE cắt AH tại D , BE cắt AC
tại F Chứng minh BE.BF = BH.BC .
Xét tam giác vuông ABF , đường cao AE ta có: 2
AB = BE.BF (1)
Xét tam giác vuông ABC , đường cao AH ta có: 2
AB = BH .BC (2)
Từ (1) và (2) suy ra : BE.BF = BH.BC . 2 AB BH 3) Chứng minh : =
và D là trung điểm của BF . 2 AC CH
Xét tam giác vuông ABC , đường cao AH ta có: 2
AB = BH .BC (1)
Xét tam giác vuông ABC , đường cao AH ta có: 2
AC = CH.BC (2) 2 AB BH .BC BH Từ (1) và (2) suy ra : = = . 2 AC CH .BC CH 1
Xét tam giác ABC vuông tại A , có đường trung tuyến AM ⇒ AM = BC = MC 2 ⇒ A ∆ MC cân tại ⇒  =  M MAC C (3) Ta lại có:  =  MAC FBA (cùng phụ  BAE ) (4)  =  C BAH (cùng phụ  HAC ) (5)
Từ (3), (4) và (5) suy ra:  =  BAH FBA hay  =  BAD DBA Suy ra: A
∆ BD cân tại D ⇒ DA = DB (6) Ta lại có:  =  FAD
DFA ( cùng phụ 2 góc bằng nhau  =  BAD DBA ) Suy ra: A
∆ FD cân tại D ⇒ DA = DF (7)
Từ (6) và (7) suy ra: DB = DF .
Suy ra : D là trung điểm của BF . (đpcm) Câu 6. Đkxđ: x ≥ 2 .
3 x = x − 7 ( x − 2) + 7
⇔ 6 x = 2x − 2 7(x − 2) +14
⇔ 2x − 2 7(x − 2) +14 − 6 x = 0
⇔ x − 6 x + 9 + x − 2 − 2 7(x − 2) + 7 = 0
⇔ ( x − )2 +( x − − )2 3 2 7 = 0 x = 9 ⇔  ⇔ x = 9(tm) x − 2 = 7
Vậy phương trình có nghiệm : x = 9 .  HẾT