Đề thi giữa kì và hướng dẫn giải môn Xử lý tín hiệu| Môn Xử lý tín hiệu| Trường Đại học Bách Khoa Hà Nội

ĐỀ THI XỬ LÍ TÍN HIỆU SỐ. K52
ĐỀ THI XỬ LÍ TÍN HIỆU SỐ. K52
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe, nhìn. A
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe, nhìn. B
Sinh viên đề nghị cán bộ coi thi ghi và ký vào bài làm đề A hoặc B,
Sinh viên đề nghị cán bộ coi thi ghi và ký vào bài làm đề A hoặc B,
nếu không bài thi sẽ 0 điểm. Nộp lại đề cùng bài làm.
nếu không bài thi sẽ 0 điểm. Nộp lại đề cùng bài làm.
Câu 1: Xác định sự tồn tại và tìm biến đổi Fourier của tín hiệu sau:
Câu 1: Cho hệ TT-BB có đáp ứng xung: ( ) = ( ) sin( ) , | | < 1 1 ℎ( ) = ( ) 3
Câu 2: Hệ TT-BB nhân quả có quan hệ vào ra:
Xác định tín hiệu ra ( ) khi tín hiệu vào là ( ) = 3 sin + 2 cos . ( ) + ( − ) = 5 ( ) + ( − 1) a. Tính ℎ(0).
Câu 2: Tìm biến đổi Z ngược của: b. Biết = 1/4, = 1/2, tính ℎ(1). 1 1 ( ) = ln(1 − 13 ) , miền hội tụ | | <
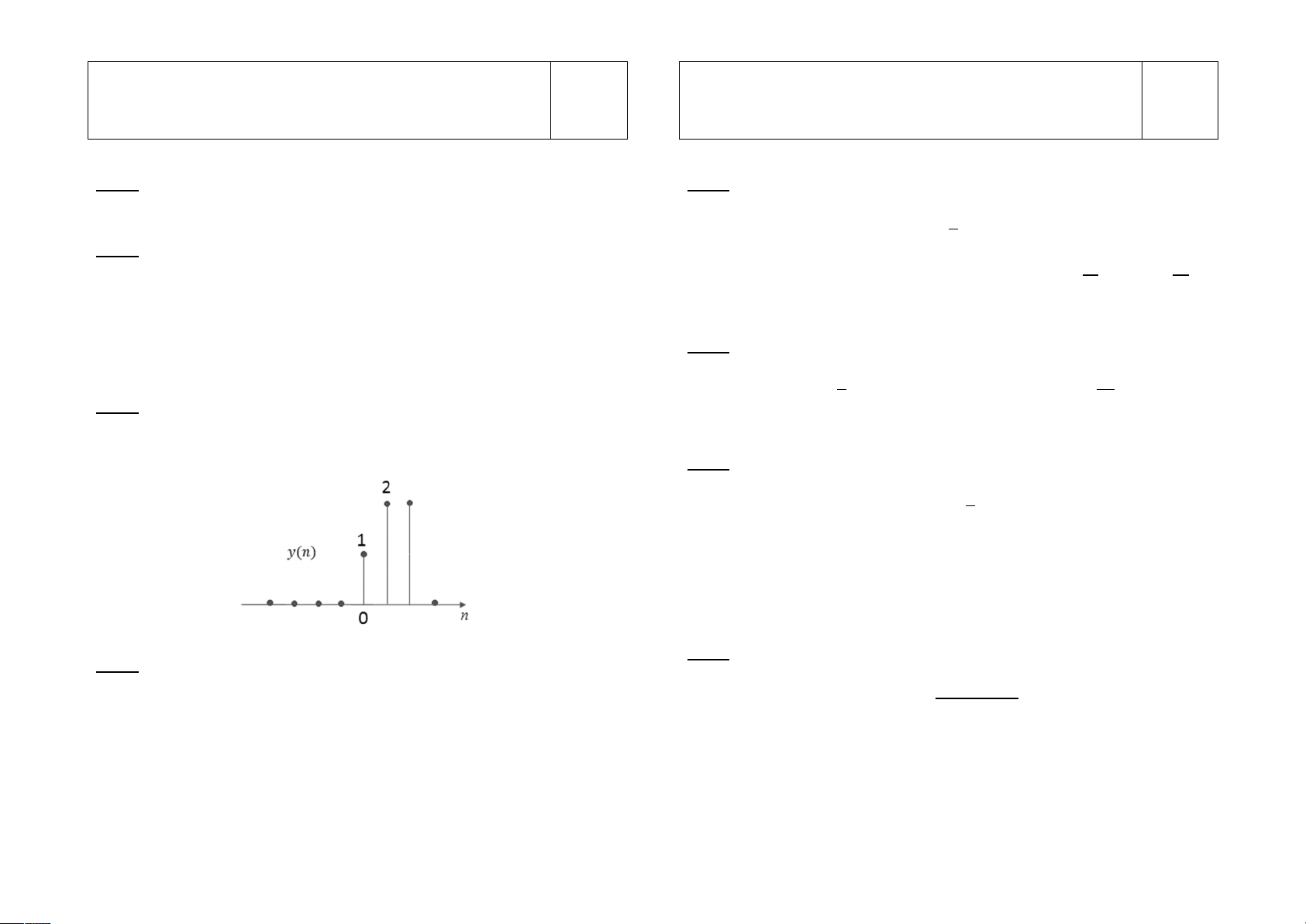
Câu 3: Cho tín hiệu ( ) như hình vẽ. Vẽ tín hiệu ( ) trong đó: 9 13 =
Câu 3: Hệ TT-BB được mô tả bởi phương trình sai phân: 1 ( ) = ( ) − ( − 1) 3
a) Đây có phải hệ truy hồi không? Vì sao? Nhận xét tính ổn định của hệ.
b) Xác định đáp ứng tần số của hệ.
c) Xác định đáp ứng biên độ và đáp ứng pha. Vẽ dạng đáp ứng biên độ.
Câu 4: Cho hệ TT-BB nhân quả có hàm truyền đạt:
Câu 4: Cho hệ thống được mô tả bằng phương trình sai phân TT-HSH sau: 3
( ) − 6 ( − 1) + 8 ( − 2) = ( ) + ( − 1) + ( − 2) ( ) = 3 + − 4 Biết ( ) = 0 khi < 0.
a) Xác định các điểm không và điểm cực.
a) Vẽ sơ đồ dạng chuẩn tắc thực hiện hệ.
b) Xét tính nhân quả, ổn định của hệ.
b) Xác định đáp ứng xung của hệ nhân quả.
c) Xác định phương trình sai phân biểu diễn quan hệ vào ra của hệ.
c) Xác định tín hiệu ra ( ) nếu biết tín hiệu vào là ( ) = 5 ( ).
d) Vẽ sơ đồ hệ thống bằng dạng chuẩn tắc. Câu 1:
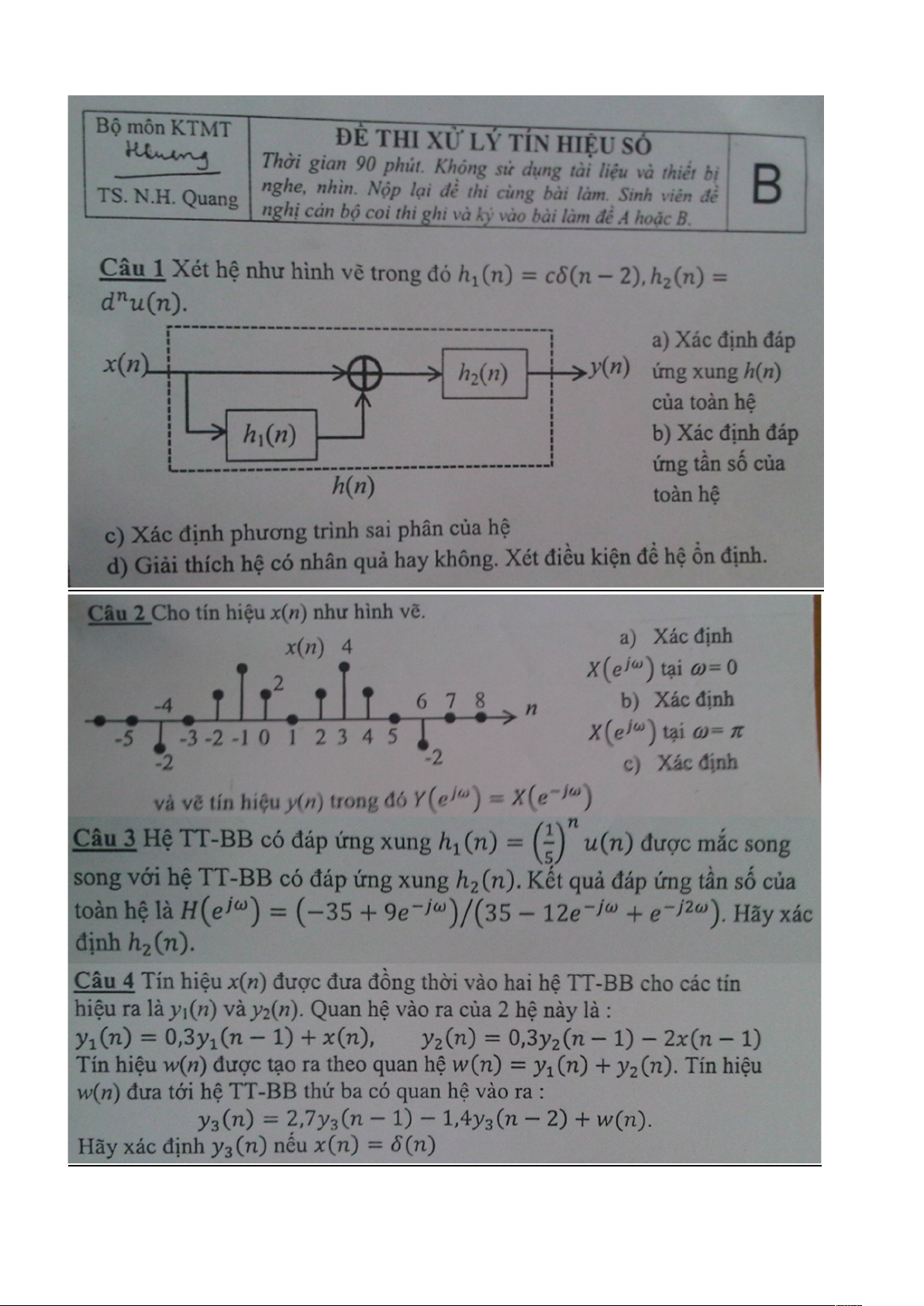
a) Xác định đáp ứng xung h(n) toàn hệ:
ℎ( ) = [ℎ ( ) + ℎ ( )] ∗ ℎ ( ), mà: ℎ ( ) = ( − 2); ℎ ( ) = ( ) Suy ra: ℎ( ) = ∑
[ℎ ( ) + ℎ ( )]. ℎ ( − ) = 1. ℎ ( − 0) + . ℎ ( − 2) = ( ) + ( − 2)
b) Xác định đáp ứng tần số toàn hệ: = ℎ( ) = + = +
Để tồn tại biến đổi Fourier thì 2 chuỗi trên phải hội tụ ⇔
< 1 ⇔ | | < 1. Khi đó: 1 1 + = + . = 1 − 1 − 1 −
c) Xác định PTSP của hệ PTSP Tổng quát: ∑ ( − ) = ∑
( − ). Đáp ứng tần số đối với PTSP này: ∑ 1 + = = ∑ 1 − Suy ra PTSP của hệ là: ( ) − ( − 1) = ( ) + ( − 2)
d) Hệ nhân quả hay không? Xét tính ổn định?
Nhận thấy h(n) = 0 khi n < 0, nên hệ nhân quả.
Điều kiện để hệ ổn định: ∑ |ℎ( )| < ∞ Có: |ℎ( )| = | | + | |
Chuỗi hội tụ khi |d|<1, phân kì khi |d|>=1. Vậy hệ ổn định khi |d|<1. Câu 2: a) Khi = 0: = ( ) = ( ) = 12 b) Khi = : = = cos( ) − ( ) = cos( ) = (−1) = ( ) = (−1) ( ) = −4 c) Theo giả thiết: ( ) = ( ). Suy ra: ( ) = ( )
Mà thực hiện đổi biến, ta được: ( ) = (− ) = (− )
Do đó ta có: ( ) = (− ). Từ đây dễ dàng vẽ được. ^^ Câu 3: Theo giả thiết: −35 + 9 5 14 1 2 = = − = − 35 − 12 + 5 − 7 − 1 1 1 − 1 − 5 7 Mà ta lại có: 1 = 1 − Từ đó: 1 1 1 = = . 1 1 − 5 5 5 2 1 1 = 2 = 2 . 1 1 − 7 7 7 Suy ra: 1 2 1 1 = − = . − 2 . 1 1 1 − 1 − 5 7 5 7 1 1 = − 2 . 5 7
Đối chiếu với công thức tổng quát: = ℎ( ). Từ đây ta rút ra: 1 1 ℎ( ) = − 2 ( ) 5 7
Hệ có h1(n) song song với hệ có h2(n) nên h(n) = h1(n) + h2(n), suy ra: 1 ℎ ( ) = −2 ( ) 7
Câu 4: giả thiết: (h1 // h2) nt h3. Gọi H1(z), H2(z), H3(z) lần lượt là hàm truyền đạt của hệ 1, 2, 3.
Hàm truyền đạt toàn hệ: ( ) = [ ( ) + ( )]. ( ) Trong đó: 1 2 1 ( ) = , ( ) = − , ( ) = 1 − 0.3 1 − 0.3 1 − 2.7 + 1.4 1 − 2 1 − 2 ⇒ ( ) = = (1 − 0.3 )(1 − 2.7 + 1.4 ) (1 − 0.3 )(1 − 2 )(1 − 0.7 ) 1 7 1 3 1 = = . − . (1 − 0.3 )(1 − 0.7 ) 4 1 − 0.7 4 1 − 0.3 Điểm cực: = 0,3;
= 0,7, đều nằm trong đường tròn đơn vị nên hệ là nhân quả và ổn định, nên: 7 3 ℎ( ) = (0.7) − (0.3) ( ) 4 4
Khi ( ) = ( ) thì ( ) = ℎ( ) = (0.7) − (0.3) ( )
ĐỀ THI XỬ LÝ TÍN HIỆU SỐ. GIỮA KÌ - K55
Thời gian 90 phút. Không sử dụng tài liệu và các thiết bị nghe, nhìn
Nộp lại đề thi cùng bài làm. Sinh viên đề nghị cán bộ coi thi ghi và A
ký vào bài làm đề A hoặc B. Nếu không bài thi sẽ không điểm.
Câu 1: Tính biến đổi z và miền hội tụ của tín hiệu ( ) = sin( ) ( )
Câu 2: Hệ TT-BB có đáp ứng tần số 1 − = 1 + 0,5
Hãy xác định tín hiệu ra nếu tín hiệu vào ( ) = sin Câu 3: Cho PT-SP ( ) − ( − 1) − ( − 2) = 3 ( )
a) Cả hệ nhân quả và hệ phản nhân quả đều có chung PT-SP trên.
Xác định hai đáp ứng xung tương ứng với hai hệ này.
b) Xét tính ổn định của hệ nhân quả và hệ phản nhân quả
c) Xác định tín hiệu ra của hệ nhân quả nếu tín hiệu vào 1 ( ) = ( ) 3 Câu 4: Xét bộ lọc số có sơ đồ khối như hình vẽ. Trong đó x(n) Z-1 Z-1 y(n) = −2 ( /3) c
a) Xác định phương trình sai phân và đáp ứng xung của hệ b) Xác định (
) . Nhận xét ứng dụng của bộ lọc số này LỜI GIẢI:
Câu 1: Xét tín hiệu ( ) = sin( ) ( ), ta có: ( ) = ( ) sin ( ) = , | | > 1 1 − 2 cos + ⇒ ( ) = { ( )} = ( ) = ( ) = , > 1 sin sin ⇒ ( ) = = , | | > | | 1 − 2 cos + 1 − 2 cos + Câu 2: 1 − = 1 + 0,5 Tín hiệu vào: ( ) = sin
. Ta có tín hiệu ra được xác định bởi: ( ) = sin + arg( 4 + Tính : 1 − 1 − cos − sin 1 + = = 2 2 = = 2 + 2 1 + 0.5(cos( ) − sin( )) 0.5 1 + 0,5 ⇒ = √4 + 4 = 2√2 + Tính arg(..): 2 arg( = arctan = arctan = arctan 1 = 2 4 Vậy ( ) = 2√2 sin + 4 4 Câu 3: a. Hàm truyền đạt: 3 3 ( ) = = = + 1 1 1 1 1 1 1 − 4 − 8 1 − 2 1 + 4 1 − 2 1 + 4 Với = ( ). 1 − = 2; = ( ). 1 + = 1 Suy ra: ( ) = 2. +
+ Với hệ nhân quả: ℎ( ) = 2. + − ( )
+ Với hệ phản nhân quả: ℎ( ) = − 2. + − (− − 1) b. Xét tính ổn định: Có: 3 3 ( ) = = 1 1 1 1 − 4 − 8 − 2 + 4
+ Điểm không bậc 2 tại gốc tọa độ + 2 điểm cực: = , = −
Đối với hệ nhân quả: | | > . Khi đó miền hội tụ chứa đường tròn đơn vị => hệ ổn định.
Đối với hệ phản nhân quả: | | < 1/4. Khi đó miền hội tụ không chứa đường tròn đơn vị
=> hệ không ổn định. c. ( ) = ( ). ( ) Mà ( ) = 2. + , ( ) = ⇒ ( ) = + + ⇒ ( ) … 1 1 1 1 − 1 − 1 + 2 3 4 Câu 4:
a) Xác định PTSP: ( ) = ( ) +
( − 1) + ( − 2) = ( ) − ( − 1) + ( − 2)
Đáp ứng xung của hệ là đầu ra của hệ khi đầu vào là xung đơn vị, do đó:
ℎ( ) = ( ) − ( − 1) + ( − 2) b) Xác định và vẽ
. Nhận xét ứng dụng bộ lọc. Ta có: = ℎ( ) = 1 − + = 1 − (cos
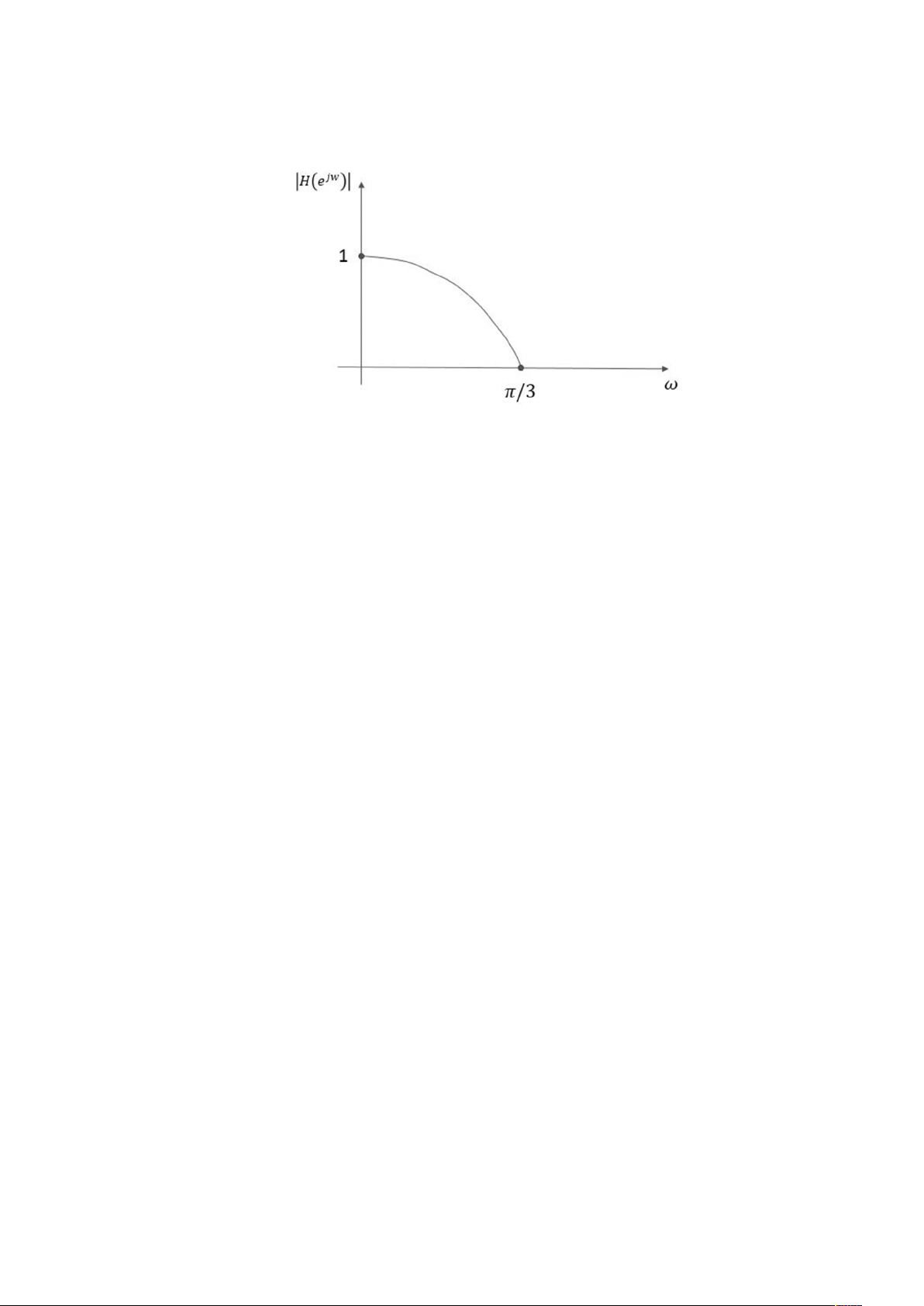
− sin ) + (cos 2 − sin 2 ) = (1 − cos + cos 2 ) + (sin − sin 2 ) Suy ra: = 1 − cos + 2 cos − 1 = cos (2 cos − 1) = sin − 2 sin cos = sin (1 − 2 cos ) ⇒ = ( ) + ( ) = |1 − 2 cos | Vẽ đáp ứng biên độ:
Nhận xét: đây là bộ lọc thông thấp.
ĐỀ THI XỬ LÍ TÍN HIỆU SỐ. 20131.GK
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe, nhìn. Sinh
viên đề nghị cán bộ coi thi ghi và ký vào bài làm đề A hoặc B, nếu B
không bài thi sẽ 0 điểm. Nộp lại đề cùng bài làm.
Câu 1: Tính biến đổi Z và miền hội tụ của tín hiệu sau: ( ) = . ( ) GIẢI: 1 1 1 ( ) = + ( ) ⇒ ( ) = ( ) + ( ) 2 2 2 1 1 1 1 = . + . , | | > | | = 1 2 1 − 2 1 − 1 − + 1 − 2 − 2 cos 1 − cos = = = , | | > 1 2(1 − )(1 − ) 2(1 − − + ) 1 − 2 cos + Câu 2: Cho tín hiệu
( ) tuần hoàn chu kì N=4 với: (0) = 4, (1) = 3, (2) = 2, (3) = 1
Tính các biến đổi Fourier rời rạc (0), (1), (2),
(3) và biểu diễn trên mặt phẳng Z. GIẢI:
Ta có biến đổi Fourier rời rạc của tín hiệu rời rạc tuần hoàn chu kì N: ( ) = ( ) . Từ giả thiết suy ra: ( ) = ( ) . = 4 + 3 + 2 + Do đó: (0) = 4 + 3.1 + 2.1 + 1 = 10
(1) = 4 − 3 − 2 + = 2 − 2 (2) = 4 − 3 + 2 − 1 = 2
(3) = 4 − 3 − 2 − = 2 − 4 , ( ) Câu 3: Cho ( ) = , ,
a) Vẽ sơ đồ dạng trực tiếp 1.
b) Vẽ sơ đồ gồm 2 hệ truy hồi bậc < 2 mắc song song.
c) Vẽ sơ đồ gồm 2 hệ nhỏ hơn mắc nối tiếp.
Câu 4: Cho ℎ( ) = ( ) + ( − 2) + ( − 4) + ( − 6)
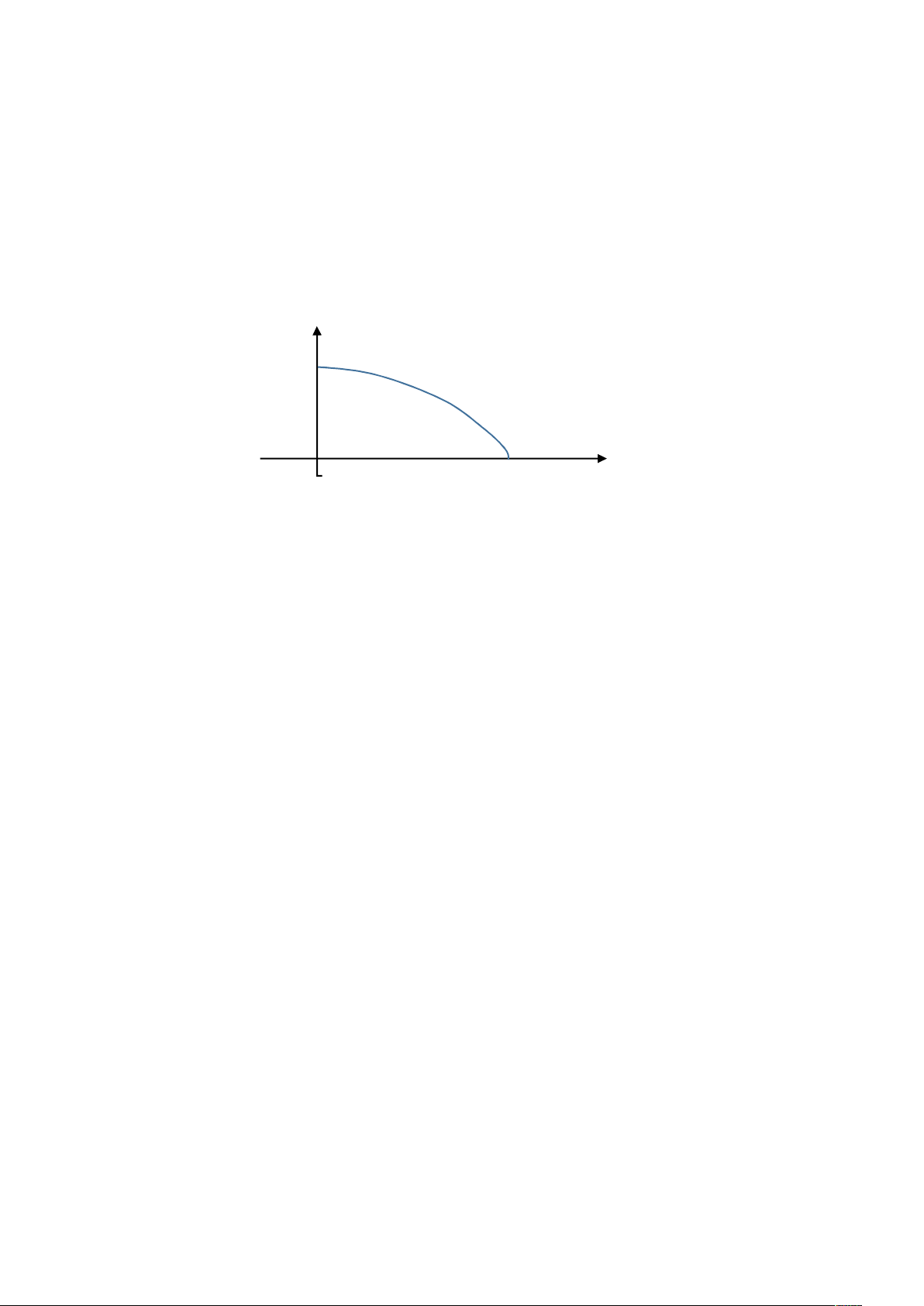
a) Tính đáp ứng tần số. = ℎ( ) = 1 + + + = 1 + 1 + = + . + = 4 cos 2 . cos
b) Tính đáp ứng biên độ. Vẽ dạng đáp ứng biên độ và nhận xét tính chất lọc của hệ. = 4|cos 2 . cos | 4 Lọc thông thấp /2
KIỂM TRA GIỮA KÌ XỬ LÍ TÍN HIỆU SỐ. 20132
Thời gian 90 phút. Không sử dụng tài liệu và thiết bị nghe, nhìn. B
Nộp lại đề cùng bài làm.
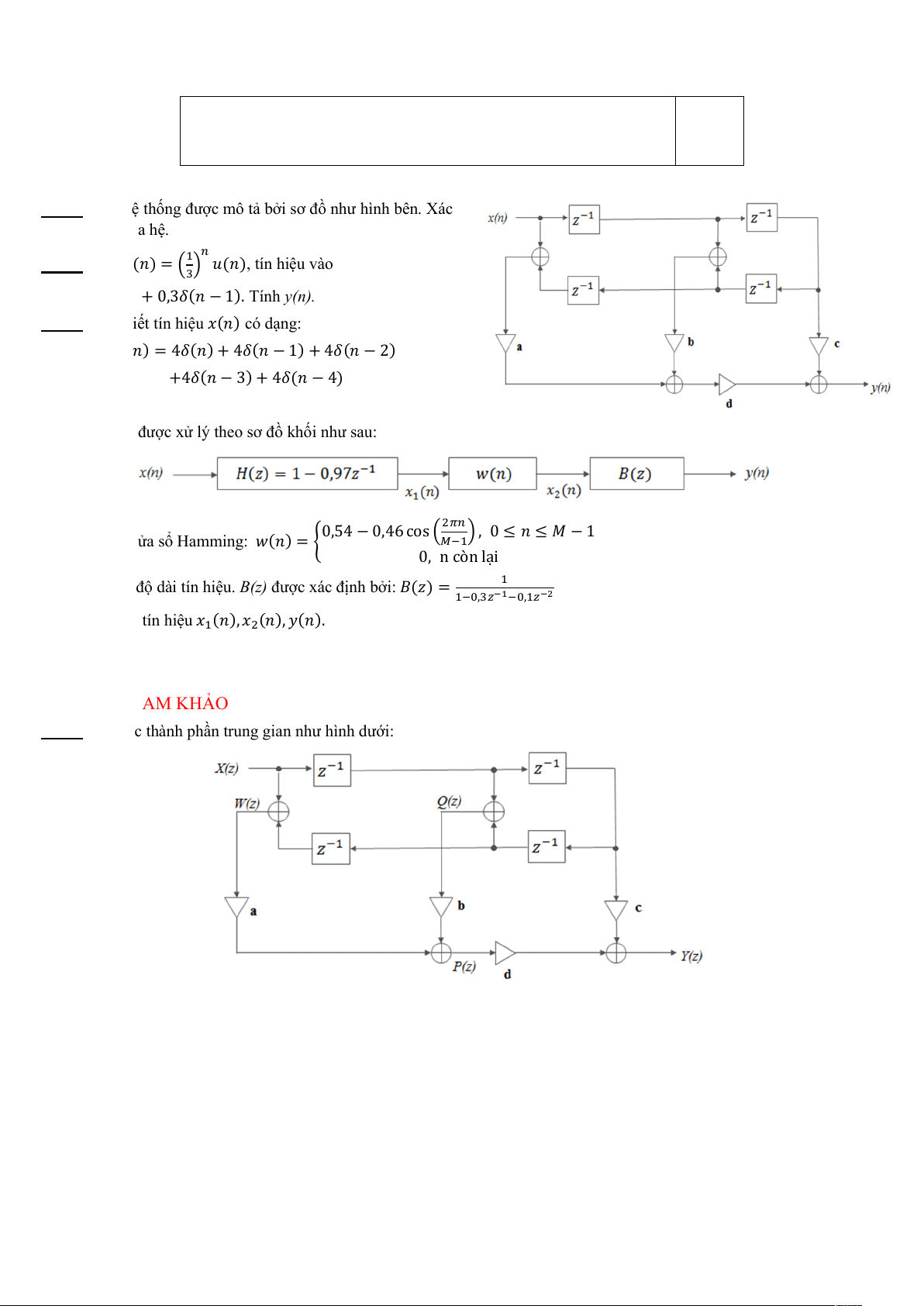
Câu 1: Cho hệ thống được mô tả bởi sơ đồ như hình bên. Xác định PT-SP của hệ. Câu 2: Cho ℎ( ) = ( ), tín hiệu vào
( ) = 2 ( ) + 0,3 ( − 1). Tính y(n).
Câu 3: Giả thiết tín hiệu ( ) có dạng:
( ) = 4 ( ) + 4 ( − 1) + 4 ( − 2) +4 ( − 3) + 4 ( − 4)
Tín hiệu ( ) được xử lý theo sơ đồ khối như sau: 0,54 − 0,46 cos , 0 ≤ ≤ − 1
( ) là hàm cửa sổ Hamming: ( ) = 0, n còn lại
trong đó M là độ dài tín hiệu. B(z) được xác định bởi: ( ) = , ,
Tính và vẽ các tín hiệu ( ), ( ), ( ). LỜI GIẢI THAM KHẢO
Câu 1: Xét các thành phần trung gian như hình dưới: Ta có: ( ) = ( ) + ( ) = (1 + ) ( ) ( ) = ( ) + ( ) = ( + ) ( ) ( ) = ( ) + ( ) = ( + + + ) ( ) ( ) = ( ) + ( ) = ( + + + + ) ( )
Thực hiện biến đổi Z ngược và áp dụng tính chất trễ, ta có PT-SP của hệ là: ( ) = ( ) + ( − 1) + ( − 2) + ( − 3) + ( − 4) Câu 2: Ta có: 2 khi = 0 ( ) = 0,3 khi = 1 0 với n còn lại
Tín hiệu ra y(n) được xác định bởi: ( ) = ( ) ∗ ℎ( ) = ( ). ℎ( − )
Do x(k) chỉ khác 0 tại = 0 ℎ ặ = 1 nên: 1 1
( ) = (0)ℎ( − 0) + (1)ℎ( − 1) = 2ℎ( ) + 0,3ℎ( − 1) = 2. ( ) + 0,3. ( − 1) 3 3 1 = [2 ( ) + 0,9 ( − 1)] 3
Câu 3: Biến đổi Z của tín hiệu x(n) là: ( ) = 4(1 + + + + ) Gọi
( ) là biến đổi Z của tín hiệu ( ), ta có: ( ) = ( ). ( ) = 4(1 + + + + )(1 − 0,97 ) = 4 + 0,12 + 0,12 + 0,12 + 0,12 − 3,88 Suy ra: ( ) = {
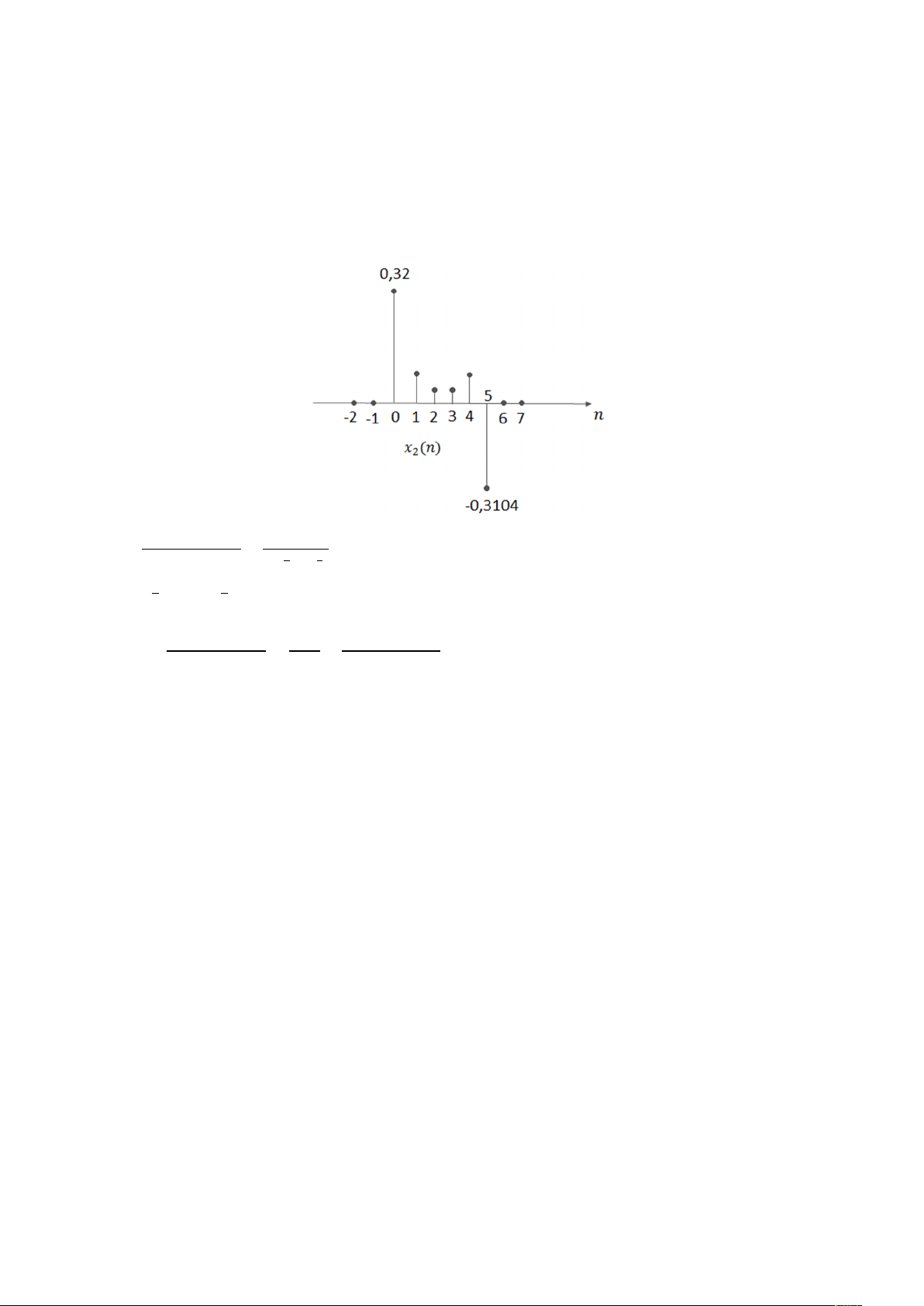
( )} = 4 ( ) + 0,12 ( − 1) + 0,12 ( − 2) + 0,12 ( − 3) + 0,12 ( − 4) − 3,88 ( − 5) Vẽ tín hiệu ( ): 0,54 − 0,46 cos , 0 ≤ ≤ 5 Độ dài tín hiệu
( ) là 6 nên ta có hàm cửa sổ Hamming với = 6: ( ) = 0, n còn lại 2
(0) = 0,54 − 0,46. cos 0 = 0,08; (1) = 0,54 − 0,46 cos ≈ 0,398 5 4 6 (2) = 0,54 − 0,46 cos
≈ 0,912; (3) = 0,54 − 0,46 cos ≈ 0,912 5 5 8 10 (4) = 0,54 − 0,46 cos
≈ 0,398; (5) = 0,54 − 0,46 cos = 0,08 5 5 Tín hiệu
( ) thu được bằng cách cho tín hiệu ( ) qua cửa sổ w(n), nên ta có: ( ) = ( ). ( ); ( ) = 0 với < 0 hoặc > 5. (0) = (0). (0) = 0,32; (1) = (1). (1) ≈ 0,0478 (2) = (2). (2) ≈ 0,1094; (3) = (3). (3) ≈ 0,1094 (4) = (4). (4) ≈ 0,0478; (5) = (5). (5) = −0,3104 Vẽ tín hiệu ( ): Ta có: ( ) = = , , Điểm cực: = ,
= − , nhận thấy cả 2 điểm cực đều thuộc đường tròn đơn vị nên hệ có hàm truyền B(z) là hệ nhân quả và ổn định. ( ) Mặt khác: ( ) = ⇒ = ⇒ ( ) − 0,3 ( ) − 0,1 ( ) = ( ) , , ( ) , ,
Sử dụng tính chất trễ của biến đổi Z, thực hiện biến đổi Z ngược cả 2 vế, ta có:
( ) − 0,3 ( − 1) − 0,1 ( − 2) = ( )
⇒ ( ) = 0,3 ( − 1) + 0,1 ( − 2) + ( )
Vì hệ có hàm truyền B(z) nhân quả; mà
( ) = 0 với < 0 nên ( ) = 0 với < 0 Từ đó suy ra:
(0) = 0,3 (−1) + 0,1 (−2) + (0) = 0 + 0 + 0,32 = 0,32 (1) = 0,3 (0) + 0,1 (−1) +
(1) = 0,3.0,32 + 0 + 0,0478 = 0,1438 (2) = 0,3 (1) + 0,1 (0) +
(2) = 0,3.0,1438 + 0,1.0,32 + 0,1094 = 0,18454 (3) = 0,3 (2) + 0,1 (1) +
(3) = 0,3.0,18454 + 0,1.0,1438 + 0,1094 = 0,17914 (4) = 0,3 (3) + 0,1 (2) +
(4) = 0,3.0,17914 + 0,1.0,18454 + 0,0478 = 0,12 (5) = 0,3 (4) + 0,1 (3) +
(5) = 0,3.0,12 + 0,1.0,17914 − 0,3104 = −0,25649 BÀI TẬP KIỂM TRA QUÁ TRÌNH 29/12/2021
Tính tổng chập x(n) và h(n) • x(n) = RECT5(n) • h(n) = u(n) – u(n – 3)
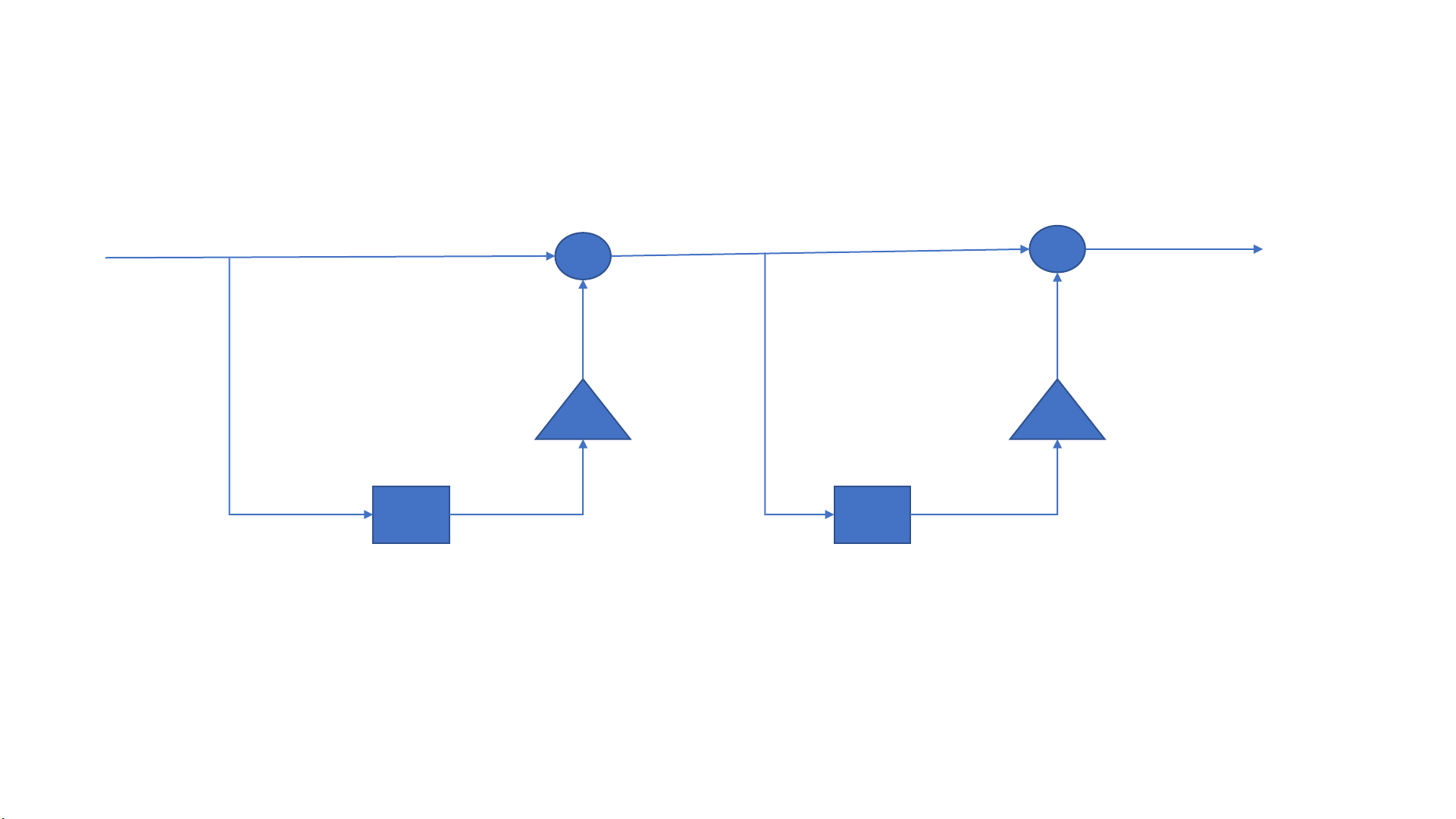
Tìm hàm truyền đạt và xác định tính ổn định
của hệ nhân quả cho bởi sơ đồ sau x(n) y(n) + + -1 -1 D D
Cho hệ TTBB và nhân quả có • h(n) = (0.5)n u(n)
• Hãy tính đáp ứng của hệ với tín hiệu vào 𝑗𝜋 • 𝑥 𝑛 = 𝐴𝑒 𝑛 2
Sử dụng Octave hãy thực hiện các thao tác sau
• Dùng hàm freqz để vẽ đáp ứng biên độ và đáp ứng pha của hệ có phương trình sai phân
• y(n) = x(n) – x(n – 1) + x(n-2)
• Nếu tín hiệu vào có tần số lấy mẫu 1000 Hz hãy xác định tần số của nhiễu
băng hẹp sẽ bị lọc bởi hệ thống này. (Nhiễu băng hẹp là loại nhiễu tone, có
năng lượng chỉ tập trung ở một khu vực rất hẹp quanh tần số nhiễu, nếu vẽ
phổ nhiễu sẽ có dạng một vạch như tín hiệu sin và cos)
(Dùng choột để xem giá trị trên hình vẽ, lấy giá trị làm tròn đến 2 chữ số sau dấu chấm) BÀI TẬP KIỂM TRA QUÁ TRÌNH 29/12/2021