Đề thi giữa kỳ Cấu trúc rời rạc | Trường Đại học CNTT Thành Phố Hồ Chí Minh

CAO THANH TÌNH
ĐẠI HỌC QUỐC GIA TP.HỒ CHÍ MINH
ĐỀ THI CUỐI KỲ MÔN CTRR
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
Học kỳ I, năm học 2017-2018
BỘ MÔN TOÁN – LÝ Ngày thi: /01/2018
Thời gian làm bài: 90 phút
Không ược sử dụng tài liệu
Câu 1. (4.0 iểm) Cho hàm Boole f(x,y,z,t), biết
f−1(0) ={0010,1011,1111, 0001, 0000}.
a) Tìm dạng nối rời chính tắc của hàm f.
b) Tìm các công thức a thức tối tiểu của hàm f.
c) Hãy vẽ sơ ồ mạch cho một công thức a thức tối tiểu của hàm f vừa tìm ược.
Câu 2. (2.0 iểm) Cho ví dụ về:
a) Đồ thị có chu trình vừa là chu trình Euler vừa là chu trình Hamilton (chỉ rõ chu trình).
b) Đồ thị có chu trình Euler và chu trình Hamilton nhưng hai chu trình này
không trùng nhau (chỉ rõ các chu trình).
c) Đồ thị có chu trình Euler (chỉ rõ chu trình) nhưng không có chu trình Hamilton.
d) Đồ thị có chu trình Hamilton (chỉ rõ chu trình) nhưng không có chu trình Euler.
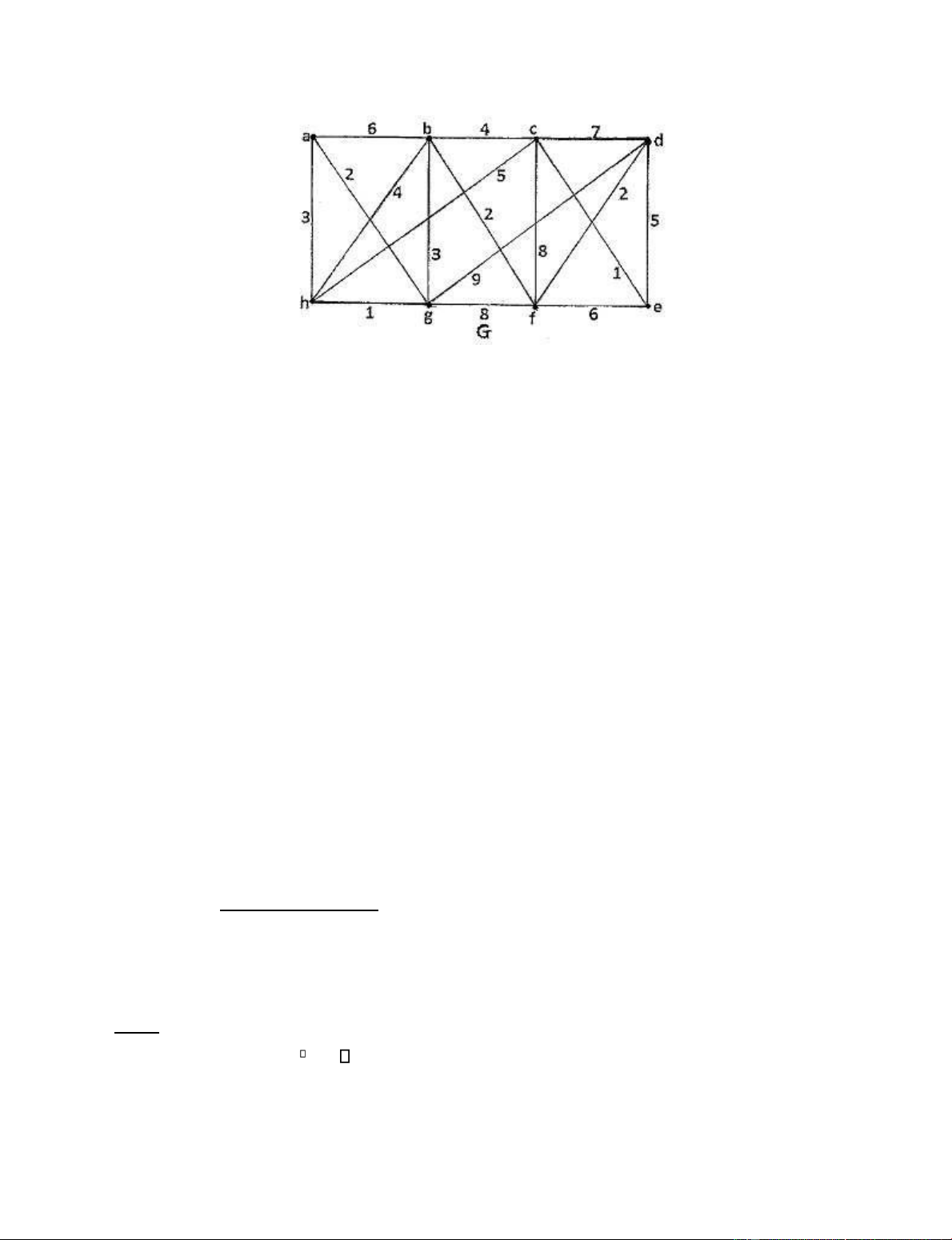
Câu 3. (4.0 iểm) Cho G là ơn ồ thị liên thông có trọng số như sau:
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
a) Tìm ường i ngắn nhất từ ỉnh a tới tất cả các ỉnh còn lại trong G và chiều dài
các ường i ó (chỉ rõ thuật toán).
b) Tìm cây khung nhỏ nhất T của G (chỉ rõ thuật toán) và tính trọng số của T.
------------------------------------ Hết Cán
bộ coi thi không giải thích gì thêm lOMoAR cPSD| 40425501
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
ĐỀ THI CUỐI KỲ MÔN CTRR
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN Học kỳ I, năm học 2019-2020 BỘ MÔN TOÁN – LÝ Ngày thi: /01/2020
Thời gian làm bài: 90 phút
Không được sử dụng tài liệu
Câu 1. (4 điểm) Cho hàm Boole 4 biến f x y z t( , , , ), biết
f 1(1) {1010, 0110,1111, 0111,1101,1000,1100}.
a) Hãy tìm dạng nối rời chính tắc của hàm f .
b) Hãy tìm các công thức đa thức tối tiểu của hàm f .
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
c) Hãy vẽ sơ đồ mạch cho một công thức đa thức tối tiểu của hàm f vừa tìm được.
Câu 2. (1 điểm) Có thể có một nhóm gồm 9 người trong đó mỗi người đều chỉ quen biết đúng
5 người khác trong nhóm hay không? Câu 3. (5 điểm)
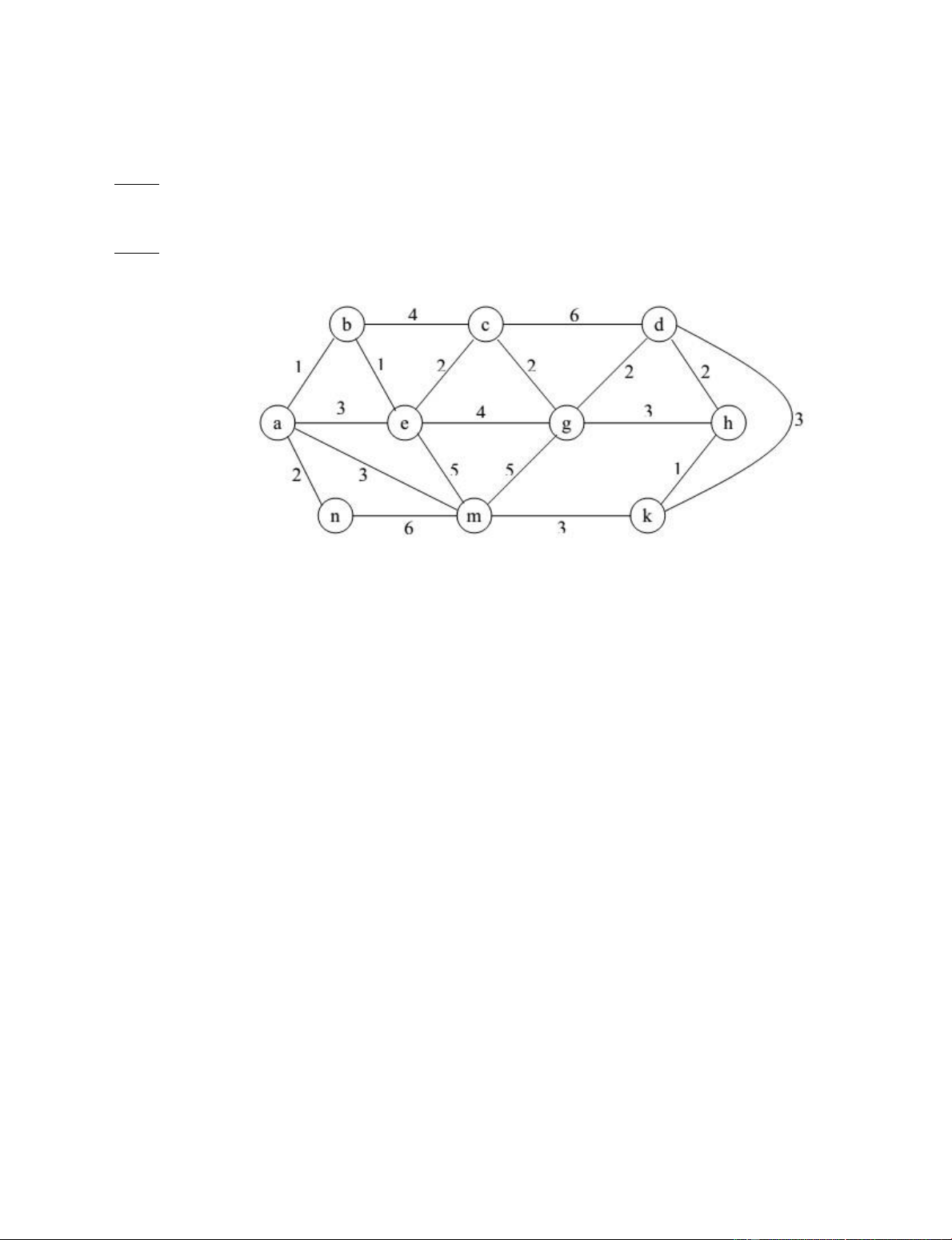
Cho đồ thị vô hướng, liên thông, có trọng số như sau:
a) Đồ thị có chu trình (đường đi) Euler không? Tại sao? Nếu có hãy chỉ ra một chu
trình (đường đi) Euler của đồ thị.
b) Hãy chỉ ra một chu trình (đường đi) Hamilton của đồ thị nếu có.
c) Hãy tìm đường đi ngắn nhất từ đỉnh a đến các đỉnh còn lại của đồ thị (chỉ rõ thuật toán).
b) Hãy tìm cây khung có trọng số lớn nhất T của đồ thị (chỉ rõ thuật toán) và tính trọng số của T.
------------------------------------ Hết
Cán bộ coi thi không giải thích gì thêm Trưởng BM Toán - Lý CAO THANH TÌNH lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)
ĐẠI HỌC QUỐC GIA TP. HỒ CHÍ MINH
ĐỀ THI CUỐI KỲ MÔN CTRR
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
Học kỳ I, năm học 2022-2023 BỘ MÔN TOÁN – LÝ Ngày thi: / /2023
Thời gian làm bài: 90 phút
Không ược sử dụng tài liệu
Câu 1. (4.0 iểm) Cho hàm Boole f theo 4 biến x y z t, , , , biết: f 1(0)
{0110, 0111, 0000, 1000, 1101}.
a) Hãy tìm dạng nối rời chính tắc của hàm f .
b) Hãy tìm các công thức a thức tối tiểu của hàm f .
c) Hãy vẽ sơ ồ mạch cho một công thức a thức tối tiểu của hàm f vừa tìm ược.
Câu 2. (1.0 iểm) Có tồn tại ồ thị vô hướng chứa 5 ỉnh với các bậc sau ây hay không? Nếu
không hãy giải thích vì sao, còn nếu có hãy vẽ ồ thị ó. a) 1, 2, 3, 4, 5 b) 1, 2, 3, 4, 4
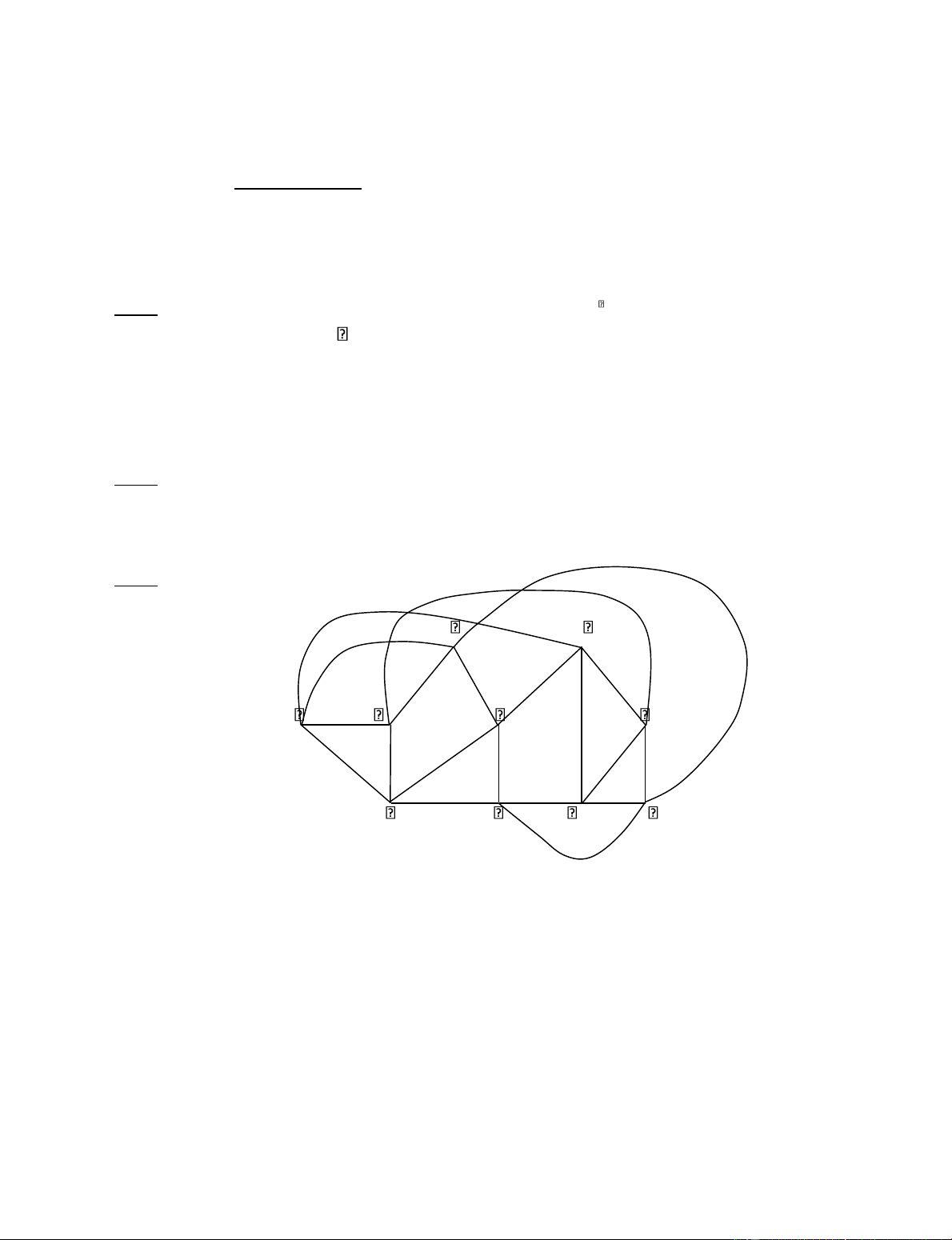
Câu 3. (5.0 iểm) Cho ồ thị G sau: 8 D F 1 5 3 4 9 5 6 A 10 B E 10 I 2 1 7 4 12 20 2 15 J 3 C G H 1
a) Hỏi G có chu trình ( ường i) Euler không? Tại sao? Nếu có hãy chỉ ra một chu trình ( ường i) Euler của G.
b) Hãy chỉ ra một chu trình ( ường i) Hamilton của G (nếu có).
c) Dùng thuật toán Dijkstra ể tìm ường i ngắn nhất từ ỉnh H ến các ỉnh còn lại của G
(trình bày thuật toán trên cùng một bảng).
d) Hãy tìm cây khung có trọng số lớn nhất T của G (trình bày thuật toán).
------------------------------------
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) Hết
Cán bộ coi thi không giải thích gì thêm Trưởng BM Toán - Lý
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com) lOMoAR cPSD| 40425501
ĐẠI HỌC QUỐC GIA TP.HỒ CHÍ MINH
ĐỀ THI GIỮA KỲ MÔN CTRR
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
Học kỳ I, năm học 2019-2020 BỘ MÔN TOÁN – LÝ Ngày thi: 02/11/2017
Thời gian làm bài: 60 phút
Không được sử dụng tài liệu Câu 1. (4,0 điểm)
a) Hãy chứng minh rằng biểu thức mệnh đề sau là một hằng đúng: (p (q r))((p q) (p r))
b) Hãy kiểm tra tính đúng đắn của mô hình suy diễn sau: q p r s p t r q t p s p
c) Hãy viết dạng phủ định của mệnh đề A và cho biết chân trị của dạng phủ định đó: A " x , y ,(xy 0) (3x y 6)"
Câu 2. (1,0 điểm) Trong kỳ thi học sinh giỏi, điểm bài thi được đánh giá bởi một số nguyên từ 0 đến 100.
Hỏi rằng ít nhất có bao nhiêu học sinh dự thi để chắc chắn tìm được hai học sinh có kết quả như nhau.
Câu 3. (1,0 điểm) Có bao nhiêu cách chọn 5 tờ tiền từ một két đựng tiền chứa những tờ tiền có mệnh giá
từ 1000đ trở lên. Giả sử thứ tự mà các tờ tiền được chọn là không quan trọng, các tờ tiền cùng loại
là không phân biệt và mỗi loại có ít nhất 5 tờ.
Câu 4. (2,0 điểm) Trên tập hợp A { 4, 3, 2,0,1,2}, ta xét quan hệ tương đương R như sau: x y,A xRy, x22x y2 2y.
a) Tìm các lớp tương đương [0] ,[1] ,[2]R R R .
b) Tìm tập thương của A theo quan hệ R. Biểu diễn sự phân hoạch của A bởi các lớp tương đương theo quan hệ R.
Câu 5. (2,0 điểm) Trên tập hợp X {1,2,3,4,5}, cho quan hệ thứ tự R {(1,1),(1,2),(1,3),(1,4),(2,2),
(2,3),(2,4),(3,3),(3,4),(4,4),(5,1),(5,2),(5,3),(5,4),(5,5)}.
a) Quan hệ thứ tự R có toàn phần không? Vì sao?
b) Vẽ biểu đồ Hasse cho (X R, ) .
c) Tìm các phần tử tối đại, tối tiểu, lớn nhất, nhỏ nhất của (X R, ) .
------------------------------------ Hết
Cán bộ coi thi không giải thích gì thêm TRƯỞNG BM TOÁN-LÝ Cao Thanh Tình lOMoAR cPSD| 40425501
ĐẠI HỌC QUỐC GIA TP.HỒ CHÍ MINH
ĐỀ THI GIỮA KỲ MÔN CTRR
TRƯỜNG ĐẠI HỌC CÔNG NGHỆ THÔNG TIN
BỘ MÔN TOÁN – LÝ
Học kỳ I, năm học 2020-2021
Ngày thi: /10/2020 Thời gian làm bài: 60 phút
Không ược sử dụng tài liệu
Câu 1. (4 iểm) a)
Hãy dùng các luật logic ể chứng minh rằng:
[q →(p r)] (p r) q(p r) q b)
Hãy mô hình hóa suy luận dưới ây về dạng mô hình suy diễn. Sau ó, hãy kiểm tra tính úng ắn của nó.
Hoa là sinh viên ngành Toán hoặc ngành Khoa học máy tính. Nếu Hoa không thích môn
Toán rời rạc thì cô ấy không phải là sinh viên ngành Khoa học máy tính. Nếu Hoa thích toán
rời rạc thì cô ấy thông minh. Biết rằng, Hoa không phải là sinh viên ngành Toán. Suy ra, Hoa là người thông minh. c)
Cho mệnh ề A '' x ¡ , y ¡ , (xy → − 0) (x 4y 5)'' . Xác ịnh chân trị của A và tìm A.
Câu 2. (1 iểm)
Mỗi sinh viên của trường UIT ều có quê ở một tỉnh thành nào ó của Việt Nam. Biết rằng,
tổng số sinh viên hiện tại của trường là hơn 6000. Hỏi cần chọn ra ít nhất bao nhiêu sinh viên
ể ảm bảo có ít nhất 50 sinh viên cùng quê?
Câu 3. (1.5 iểm)
Một cửa hàng bánh sừng bò có loại bánh bình thường, bánh có anh ào, bánh có hạnh nhân, bánh
có sôcôla, bánh táo, bánh mận. Hỏi có bao nhiêu cách chọn:
a) 24 cái bánh sao cho mỗi loại có ít nhất 2 cái?
b) 24 cái bánh sao cho có không quá 6 cái bánh táo?
Câu 4. (1.5 iểm)
Trên tập hợp X ={abc d, , , }, cho quan hệ tương ương R={(a a a c b b b d, );( , );( , );( , );
(c c, );( , );( , );( ,c a d d d b)}.
a) Hãy chỉ ra các lớp tương ương và tập thương của X theo quan hệ R.
b) Biểu diễn sự phân hoạch của X bởi các lớp tương ương theo quan hệ R.