
Preview text:
lOMoAR cPSD| 40425501
TRƯỜNG ĐẠI HỌC C NG NGHỆ TH NG TIN – ĐHQG-HCM
BAN HỌC TẬP CÔNG NGHỆ PHẦN MỀM TRƯỜNG ĐẠI HỌC ĐỀ THI THỬ
CÔNG NGHỆ THÔNG TIN
M N: CẤU TRÚC RỜI RẠC
BAN HỌC TẬP CÔNG NGHỆ PHẦN MỀM
C u 1. Cho h m Boole f theo 4 biến x, y, z,t biết:
𝑓−1(0) ={1101,1010,1000,0010,0000,0111}
a) Hªy t m dạng nối rời ch nh tắc của h m f .
b) Hªy t m cÆc c ng thức đa thức tối tiểu của h m f .
c) Hªy vẽ sơ đồ mạch cho một c ng thức đa thức tối tiểu của h m f vừa t m được.
C u 2. Cho v dụ về đơn đồ thị có 6 đỉnh:
a) Đồ thị đó vừa c chu tr nh Euler vừa c chu tr nh Hamilton (chỉ rı chu tr nh).
b) Đồ thị đó có chu trình Euler và chu trình Hamilton nhưng hai chu trình n y kh ng trøng nhau.
c) Đồ thị c chu tr nh Euler (chỉ rõ chu trình) nhưng không có chu trình Hamilton.
d) Đồ thị c chu tr nh Hamilon (chỉ rõ chu trình) nhưng không có chu trình Euler.
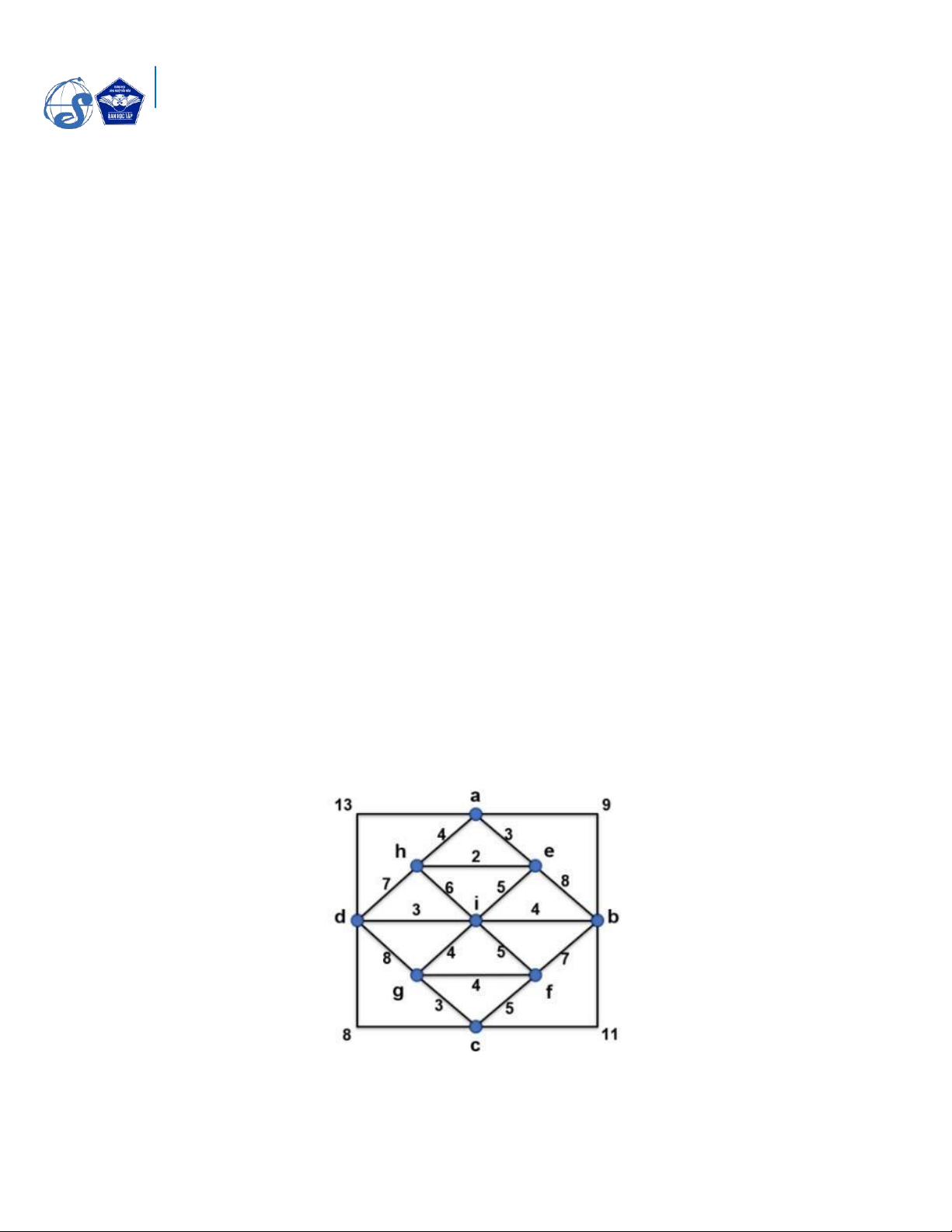
C u 3. Cho đồ thị G sau:
a) G có chu trình (đường đi) Euler không? Tại sao? Nếu c hªy chỉ ra một chu 1 lOMoAR cPSD| 40425501
TRƯỜNG ĐẠI HỌC C NG NGHỆ TH NG TIN – ĐHQG-HCM
BAN HỌC TẬP C NG NGHỆ PHẦN MỀM
tr nh đường đi) Euler của G.
b) Hªy chỉ ra một chu trình (đường đi) Hamilton của G (nếu c ).
c) Døng thuật toán Djikstra tìm đường đi ngắn nhất từ đỉnh a đến các đỉnh c n lại
của G (tr nh b y thuật toÆn trŒn cøng một bảng).
d) Hªy t m c y khung c trọng số lớn nhất T của G (tr nh b y thuật toÆn). Hết
------------------------------------------------------------------------------------------
Chœc cÆc bạn l m b i tốt! 2
Downloaded by Mai Le Thi Nguyet (hoathanvu729@gmail.com)




