

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI HỌC KÌ I NĂM HỌC 2014-2015
TRƯỜNG THPT CHU VĂN AN Môn: TOÁN - Lớp 12
Buổi thi: Chiều ngày 20 tháng 12 năm 2014 ĐỀ SỐ 2
Thời gian làm bài: 90 phút, không kể thời gian phát đề Dành cho các lớp
D1, D2, Văn, Sử, Địa, Anh, Pháp, Nhật
(Đề thi gồm 01 trang)
Câu 1 (3,0 điểm). Cho hàm số x 2 y (1). x 1
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1).
2. Tìm các giá trị thực của tham số m để đường thẳng y 3
x m cắt đồ thị (C) tại
hai điểm A, B phân biệt sao cho AB = 2 10 .
Câu 2 (3,0 điểm).
1. Cho phương trình ( 5 2)x ( 5 2)x m
18 0 (2), với m là tham số thực.
a. Giải phương trình (2) khi m = 1.
b. Tìm các giá trị của m để phương trình (2) có ít nhất một nghiệm dương.
2. Giải phương trình 2
log (x 1) log (x 3) log 2x 1 2. 2 4 2
Câu 3 (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt
phẳng (SAB) vuông góc với mặt phẳng đáy, SA = SB = 3a. Gọi H là trung điểm của AB.
1. Tính theo a thể tích khối chóp S.ABC.
2. Xác định tâm và tính theo a diện tích mặt cầu ngoại tiếp hình chóp S.HBC.
Câu 4 (1,0 điểm).
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số x2 y e
3ln(x 1) trên đoạn 0; 3 .
----------------------------- Hết -----------------------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
TRƯỜNG THPT CHU VĂN AN
ĐÁP ÁN – THANG ĐIỂM
ĐỀ THI HỌC KÌ MÔN TOÁN – Ban D – Đề 2 CÂU NỘI DUNG ĐIỂM x 2 1 Cho hàm số y (1) x 1
1 Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số (1). 2,00 *TXĐ: D = \ {1} 0.25 *Sự biến thiên:
.Giới hạn và tiệm cận: lim y 1 ; lim y ; lim y 0.25 x x1 x 1
(C) nhận đường thẳng x = -1 là tiệm cận đứng và đường thẳng y = -1 là tiệm cận ngang. 0.25 .Bảng biến thiên: 3 y ' 0, x \ {1} 0.25 2 (x 1) Lập bảng BT 0.25
HSNB trên mỗi khoảng ( ; 1) và (1; ) 0.25
*Đồ thị (vẽ bút chì trừ 0.25 điểm) 0,50
2 (d): y 3x m cắt đồ thị (C) tại hai điểm phân biệt A, B sao cho độ dài đoạn AB = 2 10 . 1,00 x 2
Phương trình hoành độ giao điểm của (C) và (d): 3x m x 1 2 3 0,25
x (m 2)x 2 m 0
(*) VT f (x) x 1
(d) cắt (C) tại hai điểm phân biệt phương trình (*) có 2 nghiệm phân biệt khác -1 0 m 10 0,25 2
m 8m 20 0 f (1) 0 m 2
A(x1; -3x1+m),B(x2; -3x2+m) (x1,x2 là nghiệm của (*)) AB2 = 10(x1- x2)2. 0,25
Áp dụng định lý Viet:AB= 2 10 (x1- x2)2 = 4 2
m 8m 56 0 m 4 6 2 (tmđk) 0,25 2
1 ( 5 2)x ( 5 2)x m 18 0 (1) 1,5 a. Khi m = 1. ( 5 2)x ( 5 2)x 18 0 . 1 0,25
Đặt ( 5 2)x t (t>0) ( 5 2)x ( nếu không giải thích: trừ 0.25) t 1
t 9 4 5(t ) m
Phương trình trở thành: t 18 0 2
t 18t 1 0 0,25 t
t 9 4 5(tm) t = 9+4 5 => x 2 ( 5 2) ( 5 2) x 2 t = 9-4 5 => x 2
( 5 2) ( 5 2) x 2 KL Tập nghiệm S = {-2;2}. 0,5
Học sinh để nghiệm dạng log (9 5) à v log (9 5) trừ 0,25 5 2 5 2
b. ( 5 2)x t . (1) thành t2 -18t + m = 0 (2).
Vì x (0;+ ) => t(0;1) nên (1) có ít nhất một nghiệm dương (2) có ít nhất một 0,25 nghiệm thuộc (0;1)
Xét hàm số y = t2 - 18t . Hsố nghịch biến trên (0;1). (2) có nghiệm thuộc (0;1) 00,25 KL: m (0;17) 2
2 log ( x 1) log (x 3) log 2x 1 2 (2) 2 4 2 1,5 1 ĐK: x> và x 3 0,25 2
(2) log (x 1) log x 3 log (2x 1) 2 2 2 2 0,5
log [( x 1) x 3 ]= log [4(2x 1)] (x 1) x 3 4(2x 1) 2 2
x 5 2 6(tm) C1: TH1: x>3 (2) 2 x 10x 1 0 0,25
x 5 2 6(l) 1 x 1(tm) TH2: x 6x - 7 0 0,25 2 x 7(l)
KL : Tập nghiệm S = { 5 2 6 ;1} 0,25
C2: NX với x TXĐ x 1 x 1 và 2x-1>0 (2) (x 1)(x 3) 4(2x 1) 2
x 2x 3 8x 4 . Giải tiếp giống C1. 2
x 2x 3 8x+4 Học sinh thiếu dấu
, chỉ giải ra được nghiệm x = 5 2 6 được 1 điểm toàn bài.
Với C2 học sinh không nêu NX trừ 0,25.
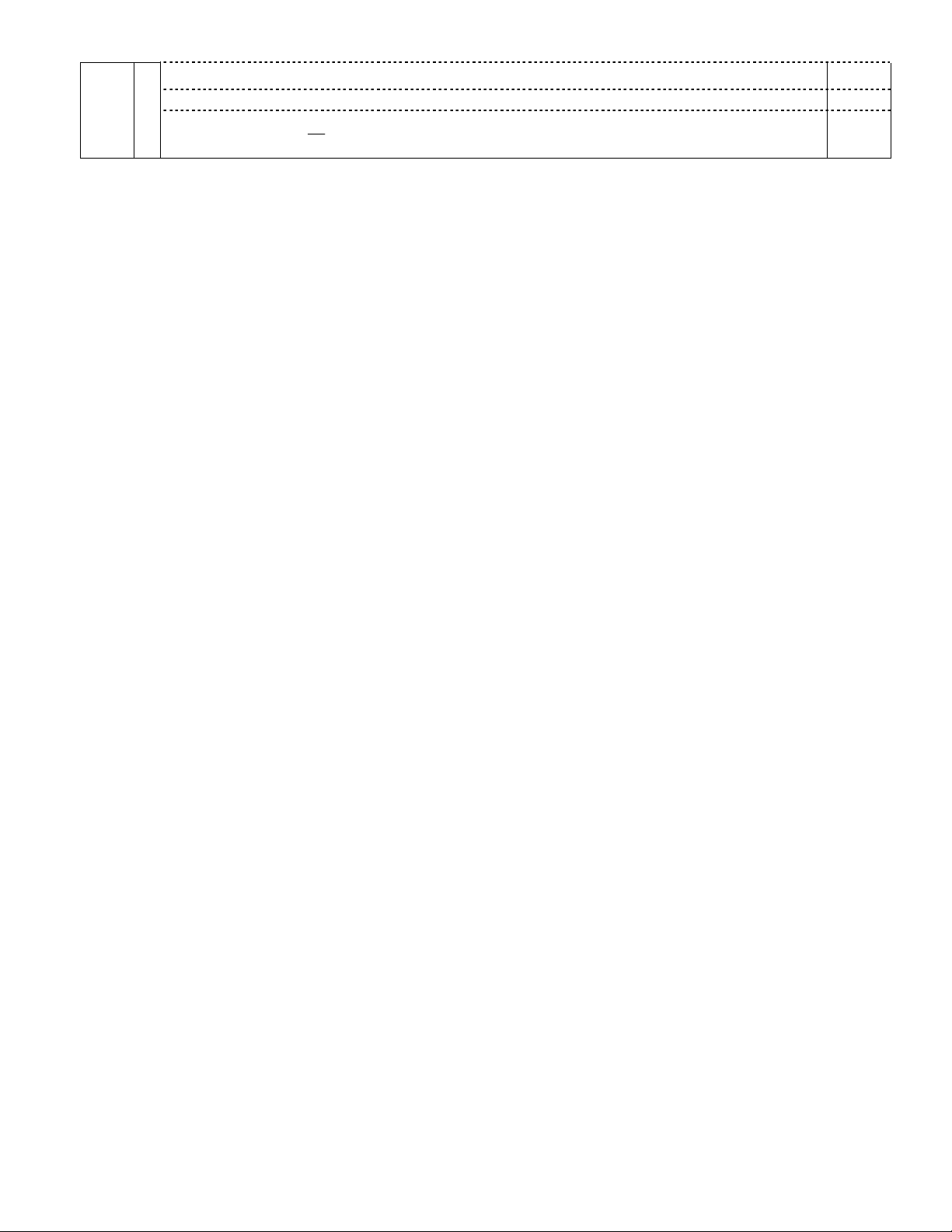
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a. Mặt phẳng (SAB) vuông góc với 3
mặt phẳng đáy, SA = SB = 3a. Gọi H là trung điểm của AB. Tính thể tích khối chóp S.ABC và 3,00
diện tích mặt cầu ngoại tiếp hình chóp S.HBC. SAB ABCD 1
SAB ABCD AB SH ( AB D C ) 0,5 Trong SAB, SH AB S Tính được 2 2 SH
SA HA 2 2a 1 0,5 SABC = AB.BC = 2a2 2 I 3 1 1 2 4 2.a S V . S .SH .2 2 . a 2 ABC ABC a 0,5 3 3 3 2 qua trung diem HC . // SH. B (ABC) C
Trong (SH, ), trung trực SH cắt tại I (I là
trung điểm củaSC). Nếu học sinh vẽ I không là 0,75
trung điểm SC thì trừ 0.25 H
Có thể nhận xét H, B cùng nhìn SC dưới một A góc vuông. D SC . a 13 0,5 Tính được R 2 2 0,25 Diện tích mặt cầu 2 S 13 a x 4
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số 2 y e 3ln(x 1) trên đoạn 3 ; 0 . 1,00 x 3 2 y ' e 0,25 x 1
Chứng minh được y’= 0 x = 2 , 0,25
2 [0;3], y(2) = 1-3ln3, y(0) = e-2 ; y(3) = e -3ln4 0,25 1
KL max y y(0)
; min y y(2) 1 3ln 3 0,25 2 x [0 ;3] e x [ 0;3]
----------------------------- HẾT -----------------------------




