

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI HỌC KÌ I NĂM HỌC 2013 - 2014
TRƯỜNG THPT CHU VĂN AN
Môn: Toán lớp 12 (Khối A)
Dành cho các lớp A, Toán, Lý, Hóa , Sinh học, Tin ĐỀ SỐ 1
Thời gian làm bài: 120 phút ,không kể thời gian phát đề
Câu I (3,0 điểm). Cho hàm số 3 2
y x 3x m (1), với m là tham số thực.
1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1.
2. Tìm m để đồ thị hàm số (1) có hai điểm cực trị A và B sao cho đường thẳng
AB đi qua điểm M(1;3).
Câu II (2,0 điểm). Giải các phương trình sau: 2 1. x 2 2x 3x 2 4 3 2. 3 6
log (3x 1) log (x 1) 3 3log ( x 5) 2 4 2
Câu III (1,0 điểm). 5
Tìm các giá trị của tham số m để phương trình sau có nghiệm trên [ ; ] : 6 6 sin x sin x 2 sin x 1 9 2.6 (m 3)2 0
Câu IV (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, 0
ABC 60 . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy.
1. Tính theo a thể tích khối chóp S.ACD.
2. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Tính theo a
khoảng cách giữa hai đường thẳng CM và SN.
3. Xác định tâm và tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
Câu V (1,0 điểm).
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y . 2 x2 e
xlog e (x ) 2 log (x ) 2 2 2 trên đoạn 3 ; 0
------------- HẾT -------------
Họ và tên thí sinh………………………………………Số báo danh…………….
ĐÁP ÁN – THANG ĐIỂM ĐỀ THI HỌC KÌ 1 – TOÁN 12 (KHỐI A) – ĐỀ SỐ 1 Câu Ý Nội dung Điểm I Cho hàm số 3 2
y x 3x m (1), với m là tham số thực. 3,0
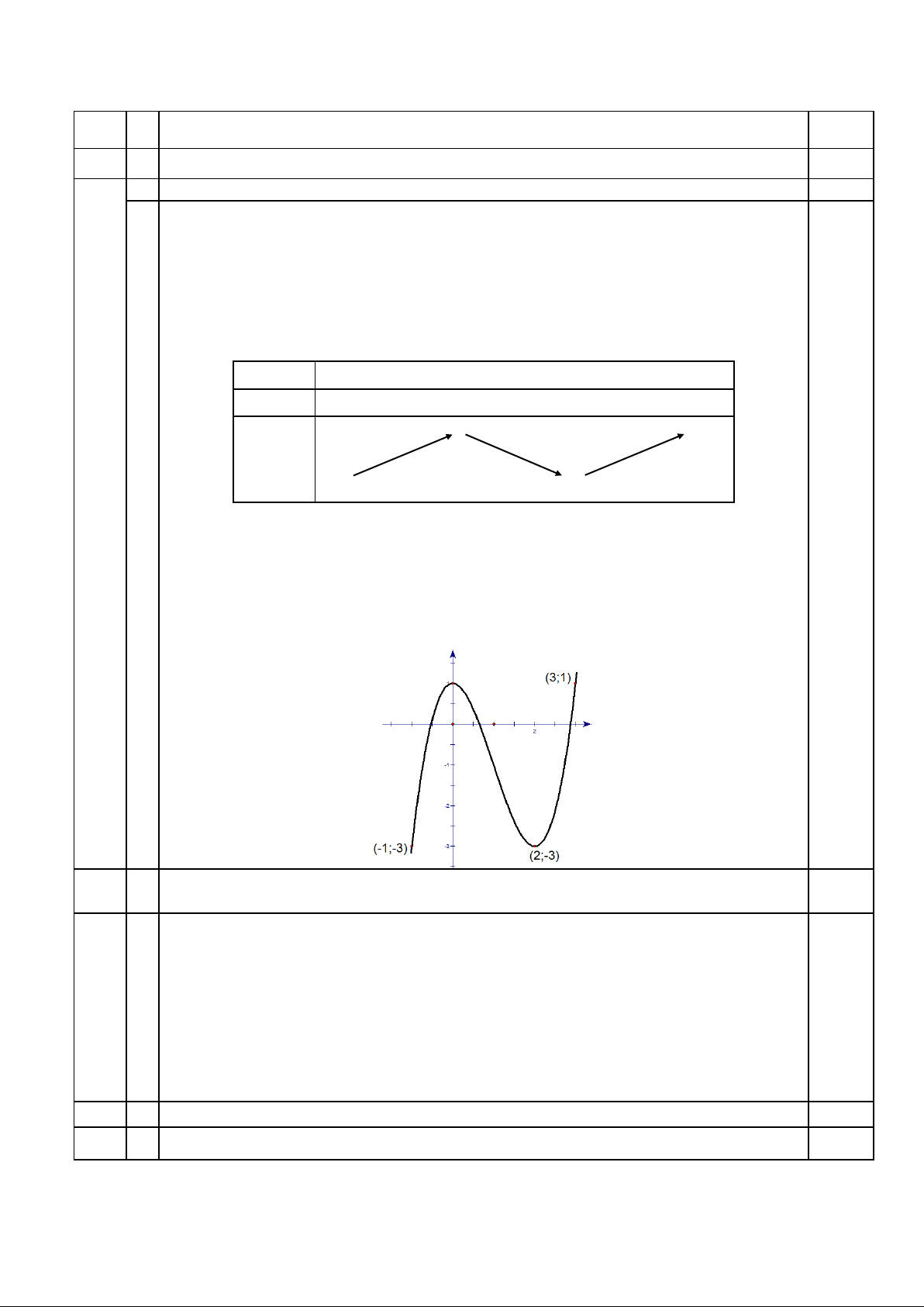
1 Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 1. (2,0 điểm) Khi m 1 : 3 2
y x 3x 1 (C) 0,25 TXĐ: D = R Sự biến thiên
- Giới hạn: lim y ; lim y x x 0,25 - 2
y ' 3x 6 ,
x y ' 0 x 0; x 2 0,25 - BBT x 0 2 y’ + 0 – 0 + 1 0,25 y – 3
- Hàm số đồng biến trên các khoảng ( ; 0)và (2; ) ;
Hàm số nghịch biến trên (0;2) 0,25
- Cực trị: Hàm số đạt cực đại tại x 0; y 1, CĐ CĐ 0,25 cực tiểu tại x 2; y 3 CT CT Đồ thị: 0,50
Tìm m để đồ thị hàm số (1) có hai điểm cực trị A và B sao cho đường thẳng AB đi
2 qua điểm M(1;3). (1,0 điểm) x 0 y(0) m Ta có 2
y ' 3x 6x ; y ' 0
x 2 y(2) m 4 0,25
(Cm) luôn có hai điểm cực trị A(0;m); B(2;m–4)
Phương trình đường thẳng AB là: 2x + y – m = 0. 0,50
Đường thẳng AB qua M(1;3) m = 5 0,25
Ghi chú: Học sinh tìm phương trình đường thẳng AB bằng cách lấy phần dư của
phép chia y cho y’ vẫn cho điểm bình thường. Không khẳng định (Cm) luôn có hai
điểm cực trị với mọi giá trị của m, trừ 0,25 điểm. II
Giải các phương trình sau: 2,0 1 2 x2 2x 3 x2 4 3 (1 điểm) TXĐ: D = R
Lôgarit hóa hai vế theo cơ số 3 ta được phương trình: 2
(x 2) log 4 2x 3x 2 0,25 3
(x 2)log 4 (x 2)(2x 1) 0,25 3 x 2 0,25 1 x log 2 3 0,25 2 2 3 6
log (3x 1) log (x 1) 3 3log
( x 5) (1 điểm) 2 4 2 1 x Điều kiện: 3 0,25 x 1
Khi đó, phương trình log (3x 1) log x 1 log 2 log (x 5) 2 2 2 2
log [(3x 1). x 1 ] log [2(x 5)] 0,25 2 2
(3x 1).(x 1) 2(x 5)
(3x 1). x 1 2(x 5)
(3x 1).(1 x) 2(x 5) 0,25 2
3x 6x 9 0 x 1 2 x 3 3x 2x 11 0 0,25
Ghi chú: Nếu học sinh nêu điều kiện sai (x > 1) và biến đổi thiếu dấu GTTĐ nhưng
vẫn ra đáp số x = 3 (đã loại giá trị x = –1), GK cho 0,25 điểm
Tìm các giá trị của tham số m để phương trình sau có nghiệm trên 5 [ ; ] : III 6 6 1,0 sin x sin x 2sin x 1 9 2.6 (m 3).2 0 sin x sin x 9 3
Chia hai vế cho 4sinx ta được phương trình: 2. 6 2 m 0,25 4 2 sin x 3 Đặt t
; ta được phương trình 2
t 2t 6 2 m (2) 2 2 3
Tìm được điều kiện: t [ ; ] 0,25 3 2 2 3
Yêu cầu bài toán tương đương với: Tìm m để (2) có nghiệm t [ ; ] 3 2 2 3
Lập bảng biến thiên của hàm số 2
f (t) t 2t 6 trên t [ ; ] 3 2 0,25 27 27 7 Từ BBT suy ra 7 2 m m 4 8 2 0,25
Ghi chú: Học sinh không tìm đúng điều kiện của t (chỉ viết t > 0) mà vẫn giải ra kết
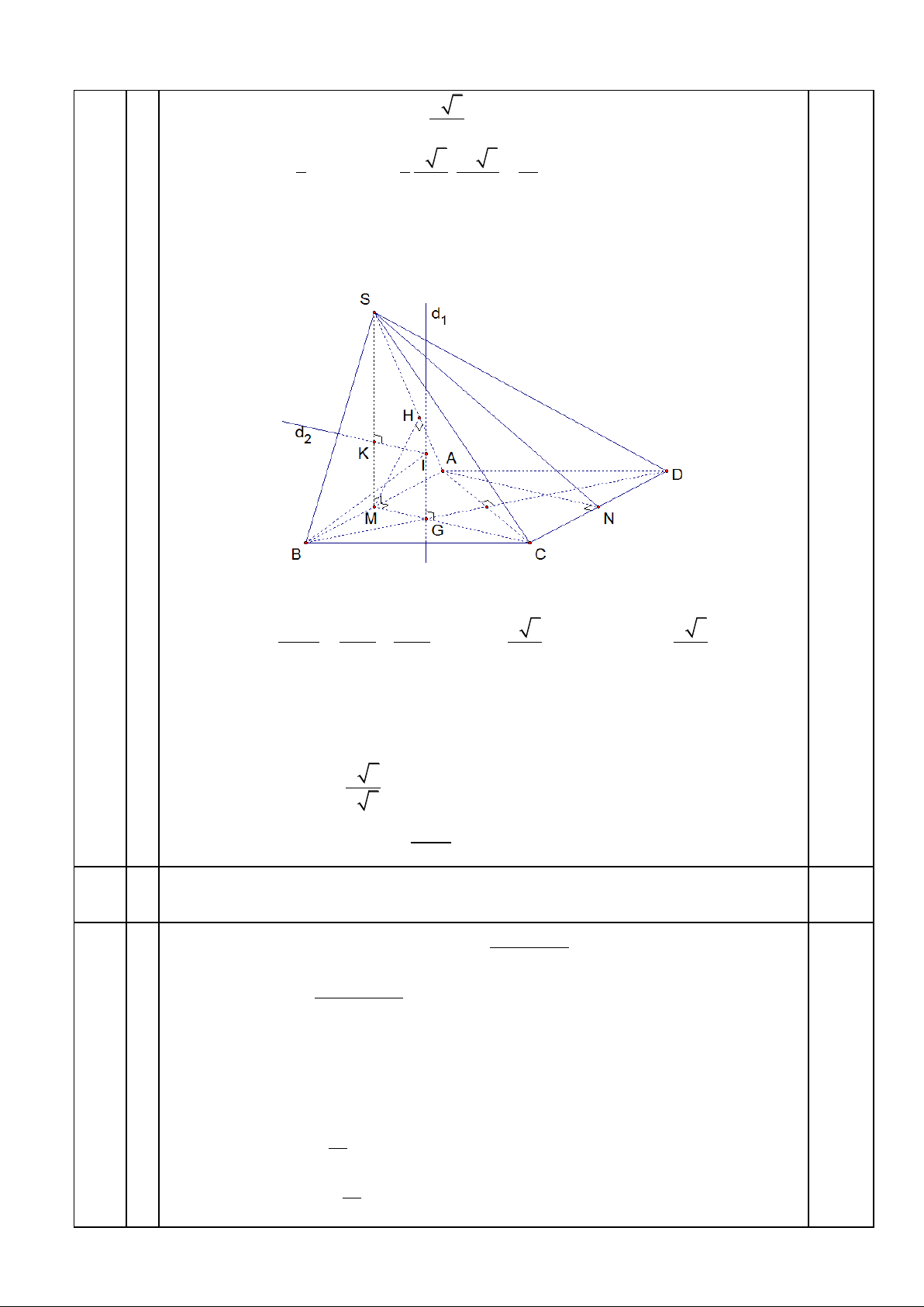
quả m, cho 0,50 điểm. Các trường hợp khác cho theo thang điểm. Cho hình chóp . Mặt bên IV
S.ABCD có đáy ABCD là hình thoi cạnh a, 0 ABC 60 SAB 3,0
là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. 1
1. Tính theo a thể tích khối chóp S.ACD. 2 a 3
Tam giác ACD đều cạnh a nên S ACD 0,25 4 SM AB SM (ACD) 0,25 a 3 0,25
Do SAB đều cạnh a SM 2 0,25 2 3 1 1 a 3 a 3 a Suy ra: V SM.S . 2 S . ACD 3 ACD 3 2 4 8
2. Gọi M và N lần lượt là trung điểm của các cạnh AB, CD. Tính theo a khoảng 0,25
cách giữa hai đường thẳng CM và SN. 0,25
CM // AN d(CM;SN) = d(CM;(SAN)) = d(M;(SAN)).
Do ACD đều AN CD AN AB AN (SAB) 0,25
Kẻ MH SA, HSA MH (SAN) d(M;(SAN)) = MH.
Tam giác SMA vuông tại M, có đường cao MH, ta có 0,25 1 1 1 a 3 a 3 MH
d(CM ; SN) . 3 2 2 2 MH MS MA 4 4 0,25
3. Xác định tâm và tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
Gọi G, K lần lượt là trọng tâm ABC và SAB. Dựng được hai trục d1, d2 và 0,25 gọi I = d1 d2.
Chỉ ra được IA = IB = IC = IS = R 0,25 a 5
Tính được R IB 2 3 0,25 2 5 a
Suy ra diện tích mặt cầu S 3
Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số V 1,0 x 2 y 2e
x log e (x 2)log (x 2) 2 2
trên tập D [0;3] . x x 1 2 2 y ' 2e
log (x 2) y" 2e 2 (x 2) ln 2 0,25 x2 1 y '' 2e 0; x
D nên phương trình y” = 0 có nhiều nhất 1 2 (x 2) ln 2
nghiệm trên D y’ = 0 có nhiều nhất 2 nghiệm trên D.
Nhận xét x = 2 là một nghiệm của phương trình y’ = 0 0,25 Hàm số x 2
g(x) 2e log (x 2) 2
liên tục trên D và g(–1).g(0) < 0 nên phương 0,25
trình y’ = 0 có 1 nghiệm thuộc (–1;0). 2
Tính được y(0)
2; y(2) 2ln 2 6; y(3) 2e 3ln 2 5log 5 2 2 e 0,25 2
Khi đó max y y(0)
2;min y y(2) 2ln 2 6 2 x [ 0;3] e x [ 0;3] - HẾT -




