


Preview text:
Sở GD và ĐT TP. Hồ Chí Minh
Trường THPT Mạc Đĩnh Chi
ĐỀ KIỂM TRA HỌC KỲ 1 NĂM HỌC 2013- 2014 MÔN TOÁN LỚP 12
Thời gian làm bài: 120 phút
A.PHẦN CHUNG DÀNH CHO TẤT CẢ CÁC THÍ SINH (7,0 điểm)
Câu 1. (3,5 điểm). Cho hàm số y = x4 - 2mx2 (1) (m là tham số thực)
a) Khảo sát hàm số và vẽ đồ thị (C1) của hàm số (1) khi m = 1.
b) Tìm giá trị của k để phương trình x4 - 2x2 - k2 + 3k - 1 = 0 có ít nhất 1 nghiệm không âm.
c) Tìm m để đồ thị của hàm số (1) có 3 điểm cực trị tạo thành tam giác vuông.
Câu 2. (1,0 điểm ). Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x2/(x4 + 1) .
Câu 3. (2,5 điểm) Cho hình chóp S.ABC có đáy là tam giác vuông tại A. SA vuông góc với mặt
phẳng(ABC) và SA = AB = AC = 2a. Gọi M, N, K lần lượt là trung điểm của SB, SC, BC.
a) Tính thể tích khối chóp S.ABC.
b) Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
c) Tính thể tích khối tứ diện AMNK.
B.PHẦN RIÊNG – PHẦN TỰ CHỌN (3,0 điểm )
Thí sinh chỉ được làm một trong hai phần (phần 1 hoặc phần 2)
Phần 1. Theo chương trình Chuẩn
Câu 4a. (2,0 điểm) Giải các phương trình 1) 12x + 27x = 2.8x
2) x = log(2x + x - 1) + xlog5
Câu 5a. (1, 0 điểm ) Cho hàm số y = x3 + x + 1 có đồ thị (C2)
Viết phương trình tiếp tuyến với đồ thị (C2) tại những điểm M(x;y) thuộc (C2) thỏa x = y.
Phần 2. Theo chương trình Nâng cao
Câu 4b. (2, 0 điểm ) Giải các phương trình
1) 8x + 18x - 2.27x = 0
2) xlog5 + log6 = log(2x + 1) + x
Câu 5b. (1, 0 điểm ) Cho hàm số y = (x + 1)/(x - 1) có đồ thị (C3)
Chứng minh rằng : Không tồn tại điểm nào thuộc (C3) để tiếp tuyến tại đó đi qua giao điểm của hai đường
tiệm cận của (C3).
ĐÁP ÁN TOÁN 12-HK1-2013-2014 Câu Nội dung Điểm I. Phần chung Câu 1. a) 4 2
m 1 y x 2x (3,5 0.25 Txđ: D = R điểm) ' 3
y 4x 4x x 0 0.25
y ' 0 x 1 lim y ; lim y 0.25 x x BBT x -1 0 1 y ' - 0 + 0 - 0 + 0.5 y 0 - 1 -1
Hs đồng biến trên mỗi khoảng ; 1 0 và ; 1
Hs nghịch biến trên mỗi khoảng ; 1
và0;1 0.25
Hs đạt cực đại tại x ; 0 y 0 CD
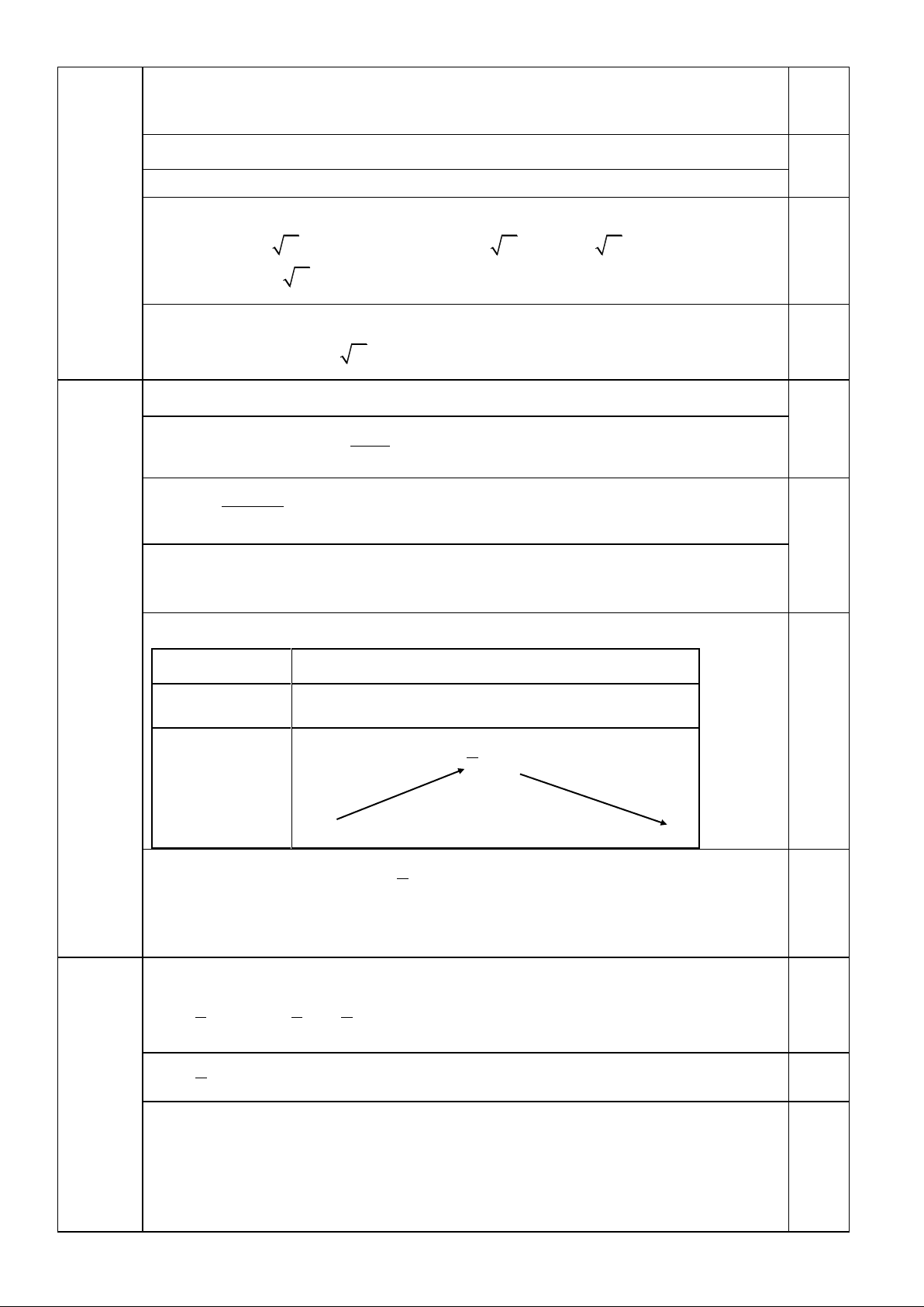
Hs đạt cực tiểu tại x ; 1 y 1 CT Đồ thị 0.5 b) 4 2 2
x 2x k 3k 1 0 4 2 2
x 2x k 3k 1 (*) 0.25
Pt (*) là pt hoành độ giao điểm của C và đt (d): 2
y k 3k 1 , d cùng phương 1 Ox. 0.25
Số nghiệm của pt (*) bẳng số điểm chung của C và (d). 1 Từ đồ thị ta có: 0.25 YCBT 2
k 3k 1 1
k 1 k 2 c) Txđ: D = R 0.25 ' 3
y 4x 4mx x 0
y ' 0 x m
m 0 ; ; ; 2 ; ; 2 A 0 0 B m m C m m 0.25 x m m 0 ABC vuông tại A m 1 0.25 2 m m Câu 2. Txđ: D = R (1,0 0.25 điể t m ). Đặt 2
t x ,t 0 g t 2 t 1 2 t 1
g 't t 2 2 1 0.25 t 1
g 't 0
; lim g t 0 t 1 x BBT t 0 1 g 't + 0 - 0.25 1 g t 2 0 0 1
max f x max g t g 1 x R t 0; 2 0.25
min f x min g t g 0 0 x R t 0;
Câu 3. a) Tính thể tích khối chóp S.ABC. (2,5 0.25 1 1 1 điể m) V S . A S S . A .A . B AC 0,25 ABC 3 3 2 4 3 V a 0.25 3
b) Tính diện tích mặt cầu ngoại tiếp hình chóp S.ABC.
Ta có: K là trung điểm của BC, suy ra K là tâm đường tròn ngoại tiếp ABC. 0.25
Từ K dựng dt () song song với SA, SA ABC , suy ra () là trục của đường
tròn ngoại tiếp ABC.
Trong mp(SAK), dựng đường trung trực d của cạnh SA, cắt SA tại E và cắt () tại I. 0.25
Suy ra I là tâm mặt cầu ngoại tiếp hình chóp S.ABC, bán kính R = IA.
AIK vuông tại K 2 2 R
AK KI a 3 0.25 2 2 S
4 R 12a 0.25 mc
c) Tính thể tích khối tứ diện AMNK. 1 0.25
M, N, K lần lượt là trung điểm của SB, SC, BC S S M NK S BC 4
SB = SC = BC SBC đều 2 S a 3 S BC V 1 AMNK V 4 SABC 1 1 4 1 3 3 0.25 V V a a AMNK SABC 4 4 3 3 +0,25 II. Phần riêng: A. Chương trình chuẩn: Câu 4a 3 x x 3 3 (2 điểm) 1) 2 0 0.25 2 2 x Đặ 3 0.25 t t 0 và 3
t t 2 0 t 1 (nhận) 2 +0,25 x 3 1 x 0 0.25 2
Vậy x 0 là nghiệm của phương trình 2) ĐK: x
2 x 1 0 0.25
Phương trình log log x x 1 5
2 x 1 0.25 x x
2 2 x 1 0.25
x 1 (nhận) 0.25 Câu 5a M ;
x y (C ) thỏa x y (1,0 2 điể 0.25 m) 3
x x 1 x x 1 y 1
Hệ số góc của tiếp tuyến: f ' 1 4 0.25
Phương trình tiếp tuyến: y 4(x ) 1 1 0.25
y 4x 3 0.25 B. Chương trình nâng cao Câu 4b. 3 x x 2 2 (2, 0
1) phương trình 2 0 0.25 3 3 điểm) x Đặ 2 0.25
t t ; t 0 và 3
t t 3 0 t 1 (nhận) 3 +0,25 x
2 1 x 0 0.25 3
Vậy x 0 là nghiệm của phương trình x 2 1
2) Phương trình x(log 5 ) 1 log 6 0.25 x 2 1 log x 2 log 6 x 2 1 x 2 6 6 0.25 x 2 1 x 2 2 x x 2
2 6 0 x 2 2 0.25 x 2 3 x 1 0.25
Câu 5b. Giao điểm của hai tiệm cận I ;11 0.25 (1, 0 điểm )
Đường thẳng (d) qua I có hệ số góc là k: y k(x ) 1 1 0.25
x 1 k(x )11 ( )1 x 1
(d) tiếp xúc với C có nghiệm x 3 0.25 2 k (2) (x )2 1 x 1 2 Thế (2) vào (1) ta có:
1 1 3 (sai) x 1 (x ) 1 0.25
Vậy không tồn tại điểm nào thuộc C để tiếp tuyến tại đó đi qua giao điểm của hai 3
đường tiệm cận của C . 3




