Đề thi HK1 lớp 12 trường Nguyễn Công Phương – Quảng Ngãi 2013 – 2014

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2013 – 2014 .Mời bạn đọc đón xem.

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

4 trang 8 tháng trước

Tác giả:

Profile Lan Tường
SỞ GD & ĐT QUẢNG NGÃI
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG
KIỂM TRA HỌC KỲ I - NĂM HỌC 2013-2014
Môn: TOÁN 12
Thời gian làm bài: 90 phút (Không kể giao đề)
Bài 1 (4 điểm): Cho hàm số
21
1
x
y
x
(C)
a) Khảo sát sự biến thiên và vẽ đồ thị (C).
b) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ bằng 2.
c) Xác định m để (C) cắt đường thẳng d :
y x m
tại 2 điểm phân biệt.
Bài 2 (2 điểm):
a) Giải phương trình:
4 16.4 17 0
xx
b) Giải bất phương trình:
2
0,5
log ( 5 6) 1xx
Bài 3 (1 điểm): Tìm GTLN, GTNN của hàm số
lnx
y=
x
trên đoạn [1; e
3
]
Bài 4 (3 điểm): Cho hình chóp S.ABCD, đáy là hình chữ nhật ABCD có
,
cạnh bên SA vuông góc với mặt đáy (ABCD), cạnh bên SB tạo với mặt đáy (ABCD) một góc
bằng
0
30
. Gọi H là trung điểm của SD.
a) Chứng minh rằng DC vuông góc với AH.
b) Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
c) Tính thể tích khối chóp H.ABC .
----------- HẾT ----------
SỞ GD & ĐT QUẢNG NGÃI
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG
KIỂM TRA HỌC KỲ I - NĂM HỌC 2013-2014
Môn: TOÁN 12
Thời gian làm bài: 90 phút (Không kể giao đề)
Bài 1 (4 điểm): Cho hàm số
21
1
x
y
x
(C)
a) Khảo sát sự biến thiên và vẽ đồ thị (C).
b) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ bằng 2.
c) Xác định m để (C) cắt đường thẳng d :
y x m
tại 2 điểm phân biệt.
Bài 2 (2 điểm):
a) Giải phương trình:
4 16.4 17 0
xx
b) Giải bất phương trình:
2
0,5
log ( 5 6) 1xx
Bài 3 (1 điểm): Tìm GTLN, GTNN của hàm số
lnx
y=
x
trên đoạn [1; e
3
]
Bài 4 (3 điểm): Cho hình chóp S.ABCD, đáy là hình chữ nhật ABCD có
,
cạnh bên SA vuông góc với mặt đáy (ABCD), cạnh bên SB tạo với mặt đáy (ABCD) một góc
bằng
0
30
. Gọi H là trung điểm của SD.
a) Chứng minh rằng DC vuông góc với AH.
b) Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
c) Tính thể tích khối chóp H.ABC .
----------- HẾT ----------
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI HKI MÔN TOÁN 12
Bài
Đáp án
Thang điểm
Bài 1
( 4đ )
1.TXĐ
\1D
2.Sự biến thiên
lim 2
x
y

suy ra y =2 là tiệm cận ngang.
11
lim ; lim
xx
yy


 
suy ra x=1 là tiệm cận đứng.
2
3
1
y
x
Bảng biến thiên
x

1

y
y
2


2
Hàm số nghịch biến trên
;1 , 1; 
3. Đồ thị
8
6
4
2
2
4
6
15
10
5
5
10
15
x
( )
=
2
∙
x
+ 1
x
1
b. Gọi
00
;xy
là tọa độ tiếp điểm. Theo đề ta có
0 0 0
2 5, 3x y y x
.
Pttt cần tìm là
3 2 5 3 11y x x
.
c. Phương trình hoành độ giao điểm của (C) và đường thẳng d : y=x+m là
2
21
1
2 1 1 , 1
3 1 0 ( )
x
xm
x
x x x m x
x m x m

Ta có x=1 không là nghiệm của pt
()
. Do đó, (C) cắt d tại 2 điểm phân
biệt khi
()
0

.
2
2
()
3 4 1 2 13 0m m m m m
0,25
1.25
0.5
0.5
0.5
0.5
Vậy (C) và d luôn cắt nhau tại 2 điểm phân biệt với mọi giá trị của m.
0.5
2a
4 16.4 17 0
xx
Đặt t =
4
x
, t>0
Phương trình đã cho trở thành:
2
16
17 0 17 16 0
1( )
16( )
t t t
t
tN
tN
Với t=1 thì
0
4 1 4 0
x
x
Với t=16 thì
2
4 16 4 2
x
x
Vậy phương trình có hai nghiệm x=0, x=2.
0,25
0,25
0,25
0,25
2b
2
2
0,5
2
2
2
5 6 0
log ( 5 6) 1
5 6 2
5 6 0 2 3 1 2
1 4 3 4
5 4 0
1;2 3;4
xx
xx
xx
x x x x x
xx
xx
S




0,25
0,5
0,25
Bài 3
(1,0 đ)
Hàm số liên tục trên đoạn [ 1; e
3
]
...............................................................................................................................................................................
2 ln
'
2
x
y
xx
;
2
y' 0 x e
...............................................................................................................................................................................
23
3
23
( ) ; ( ) ; (1) 0 y e y e y
e
e
...............................................................................................................................................................................
33
2
0;e 0;e
2
miny = 0khi x =1; maxy = khix e
e
(0,25 đ)
....................
(0,25 đ)
....................
(0,25 đ)
....................
(0,25 đ)
Bài 4
a)
()
()
DC AD
DC SAD
DC SA
AH SAD DC AH

b)
0
90SAC
()
()
BC SAB BC SB
CD SCD CD SD
Ba điểm A,B,D nhìn đoạn SC dưới 1 góc vuông nên 5 điểm A,B,C,D,S nằm
trên mặt cầu đường kính SC.Tâm mặt cầu là trung điểm I của đoạn SC.
SA=ABtan30
o
=a
0.5
0.5
0.5
22
3SC SA AC a
Suy ra bán kính mặt cầu
13
22
a
R SC
c)Diện tích tam giác ABC bằng
2
13
.
22
a
AB BC
Đường cao HK bằng
2
a
Thể tích khối chóp H.ABC bằng
3
3
12
a
(đvtt)
0.5
0.25
0.25
0.5
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:


SỞ GD & ĐT QUẢNG NGÃI
KIỂM TRA HỌC KỲ I - NĂM HỌC 2013-2014
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG Môn: TOÁN 12
Thời gian làm bài: 90 phút (Không kể giao đề) Bài 1 x
(4 điểm): Cho hàm số 2 1 y  (C) x 1
a) Khảo sát sự biến thiên và vẽ đồ thị (C).
b) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ bằng 2.
c) Xác định m để (C) cắt đường thẳng d : y x m tại 2 điểm phân biệt. Bài 2 (2 điểm): 
a) Giải phương trình: 4x 16.4 x 17  0
b) Giải bất phương trình: 2
log (x  5x  6)  1  0,5
Bài 3 (1 điểm): Tìm GTLN, GTNN của hàm số lnx y = trên đoạn [1; e3 ] x
Bài 4 (3 điểm): Cho hình chóp S.ABCD, đáy là hình chữ nhật ABCD có AD  ,
a AB a 3 ,
cạnh bên SA vuông góc với mặt đáy (ABCD), cạnh bên SB tạo với mặt đáy (ABCD) một góc bằng 0
30 . Gọi H là trung điểm của SD.
a) Chứng minh rằng DC vuông góc với AH.
b) Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
c) Tính thể tích khối chóp H.ABC . ----------- HẾT ----------
SỞ GD & ĐT QUẢNG NGÃI
KIỂM TRA HỌC KỲ I - NĂM HỌC 2013-2014
TRƯỜNG THPT NGUYỄN CÔNG PHƯƠNG Môn: TOÁN 12
Thời gian làm bài: 90 phút (Không kể giao đề) Bài 1 x
(4 điểm): Cho hàm số 2 1 y  (C) x 1
a) Khảo sát sự biến thiên và vẽ đồ thị (C).
b) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ bằng 2.
c) Xác định m để (C) cắt đường thẳng d : y x m tại 2 điểm phân biệt. Bài 2 (2 điểm): 
a) Giải phương trình: 4x 16.4 x 17  0
b) Giải bất phương trình: 2
log (x  5x  6)  1  0,5
Bài 3 (1 điểm): Tìm GTLN, GTNN của hàm số lnx y = trên đoạn [1; e3 ] x
Bài 4 (3 điểm): Cho hình chóp S.ABCD, đáy là hình chữ nhật ABCD có AD  ,
a AB a 3 ,
cạnh bên SA vuông góc với mặt đáy (ABCD), cạnh bên SB tạo với mặt đáy (ABCD) một góc bằng 0
30 . Gọi H là trung điểm của SD.
a) Chứng minh rằng DC vuông góc với AH.
b) Xác định tâm và tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD .
c) Tính thể tích khối chóp H.ABC . ----------- HẾT ----------
ĐÁP ÁN VÀ THANG ĐIỂM ĐỀ THI HKI MÔN TOÁN 12 Bài Đáp án Thang điểm Bài 1 0,25 1.TXĐ D  \   1 2.Sự biến thiên ( 4đ )  1.25
lim y  2 suy ra y =2 là tiệm cận ngang. x lim y  ;
 lim y   suy ra x=1 là tiệm cận đứng.   x 1  x 1   3  y   x  2 1  Bảng biến thiên x  1  y   y 2   2
 Hàm số nghịch biến trên   ;1 , 1;  3. Đồ thị 2∙x + 1 8 (x) = 0.5 x 1 6 4 2 15 10 5 5 10 15 2 4 6
b. Gọi  x ; y là tọa độ tiếp điểm. Theo đề ta có 0 0 
x  2  y  5, yx  3  . 0 0  0 0.5
Pttt cần tìm là y  3
 x  2  5  3  x 11.
c. Phương trình hoành độ giao điểm của (C) và đường thẳng d : y=x+m là 0.5 2x 1  x m x 1 
2x 1   x  
1  x m , x   1 2
x  m 3 x m 1 0 ( ) 
Ta có x=1 không là nghiệm của pt ( )
 . Do đó, (C) cắt d tại 2 điểm phân biệt khi   0 . () 0.5           
m 32 4m  2 1 m 2m 13 0 m ( )
Vậy (C) và d luôn cắt nhau tại 2 điểm phân biệt với mọi giá trị của m. 0.5 2a
4x 16.4x 17  0
Đặt t = 4x , t>0
Phương trình đã cho trở thành: 0,25 16 2 t
17  0  t 17t 16  0 tt  1(N )   t 16(N) Với t=1 thì x 0
4  1  4  x  0 0,25 Với t=16 thì x 2
4  16  4  x  2
Vậy phương trình có hai nghiệm x=0, x=2. 0,25 0,25 2b 2
x 5x  6  0 2
log (x  5x  6)  1    0,5 0,25 2
x 5x  6  2 2
x 5x  6  0
x  2  x  3 1   x  2       2
x 5x  4  0 1   x  4 3  x  4 0,5
S  1; 2  3; 4 0,25
Hàm số liên tục trên đoạn [ 1; e3 ] (0,25 đ)
............................................................................................................................................................................... .................... 2  ln x y '  ; 2 y '  0  x  e (0,25 đ) Bài 3 2x x
................................................................................................................................................................ ............... .................... (1,0 đ) 2 3 2 3 y(e )  ; y(e )  ; y(1)  0 (0,25 đ) 3 e e
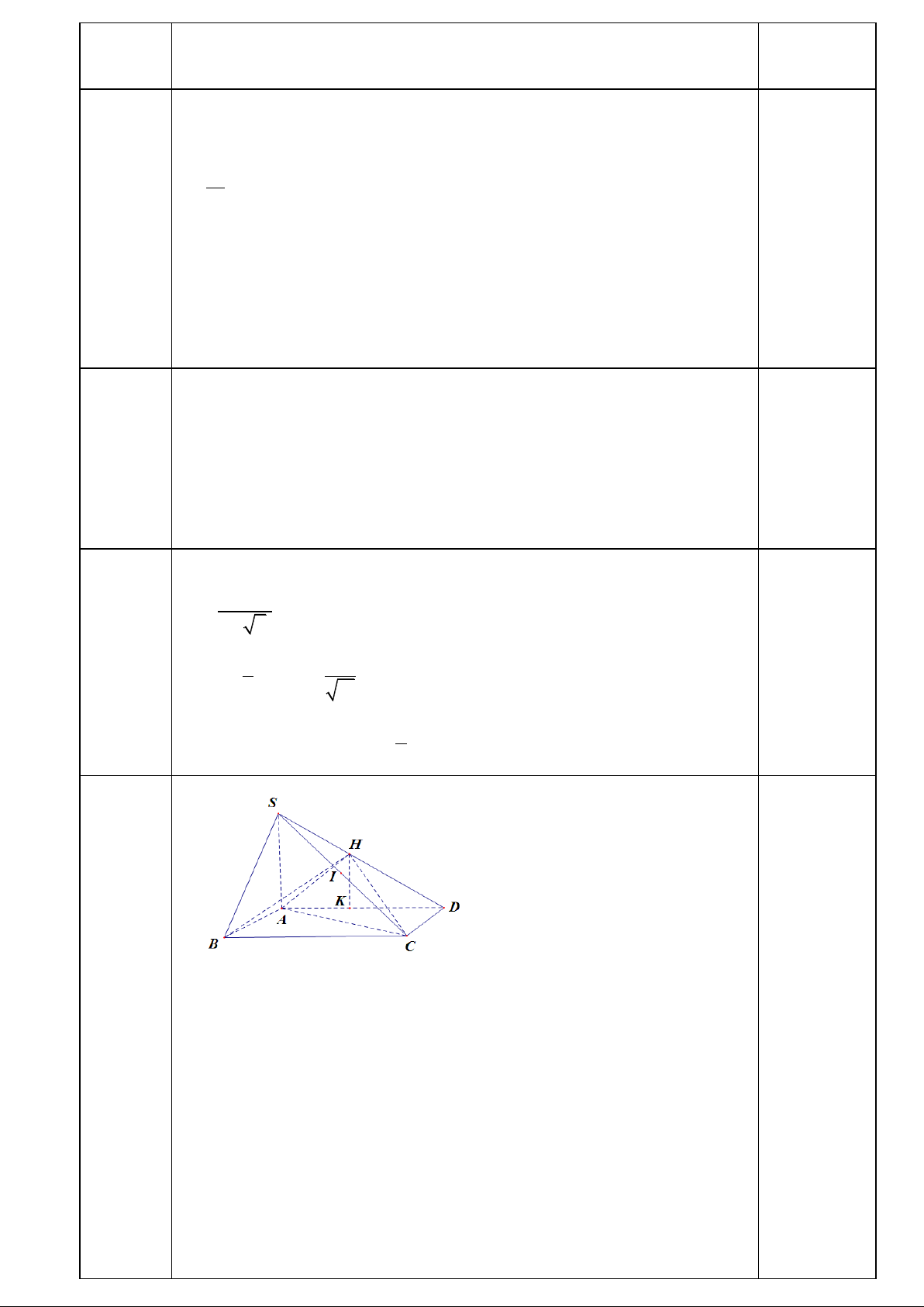
............................................................................................................................................................................... .................... 2 2 miny = 0 khi x = 1; maxy = khi x  e (0,25 đ) 3 3 0;e  0;e  e     Bài 4 0.5 a) DC AD
  DC  (SAD) DC SA  0.5
AH  (SAD)  DC AH b) 0 SAC  90
BC  (SAB)  BC SB
CD  (SCD)  CD SD 0.5
Ba điểm A,B,D nhìn đoạn SC dưới 1 góc vuông nên 5 điểm A,B,C,D,S nằm
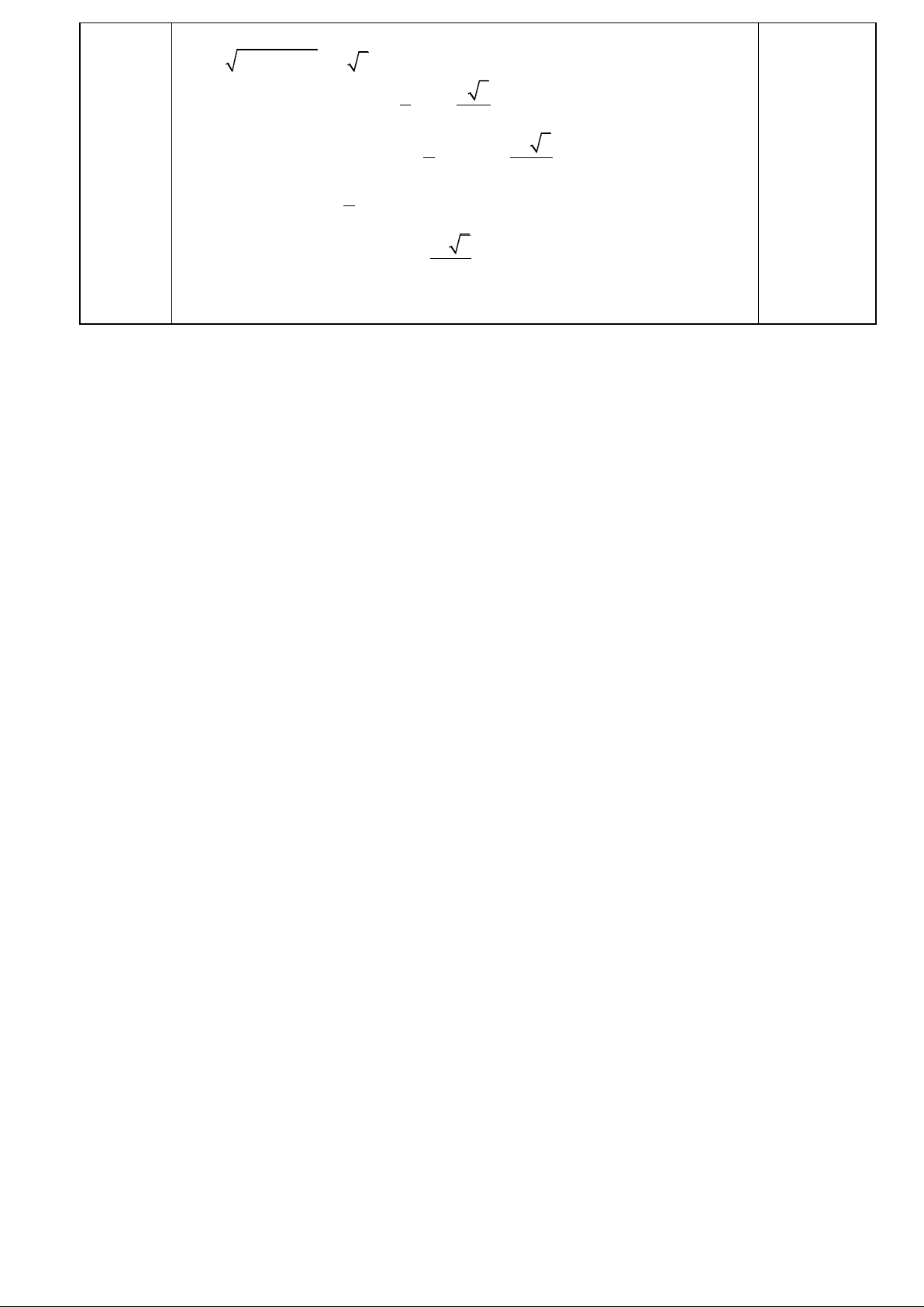
trên mặt cầu đường kính SC.Tâm mặt cầu là trung điểm I của đoạn SC. SA=ABtan30o =a 2 2 SC
SA AC a 3 0.5 Suy ra bán kính mặt cầu 1 a 3 R SC  2 2 2
c)Diện tích tam giác ABC bằng 1 a 3 . AB BC  0.25 2 2
Đường cao HK bằng a 0.25 2 3 0.5
Thể tích khối chóp H.ABC bằng a 3 (đvtt) 12