



Preview text:
SỞ G IÁO D ỤC V À Đ ÀO ĐỀ KIỂM TRA HỌC KỲ I THÀ H NH PHỐ H Ồ CHÍ M INH NĂM HỌC: 2019-2020 TRƯỜNG T HPT T PHÚ L ÂM MÔN: TOÁN – LỚP 10
Thời gian làm bài: 90 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên học sinh: ……………………………………….- Lớp: ……… – SBD: ……………..
Câu 1. (2.0 điểm) Cho A (2;3) và B (0;6), xác định A B, A B, A \ B,C A và biểu diễn chúng trên trục số. Câu 2. (1.5 điểm)
a) Tìm tập xác định của hàm số 3x 1 y ; 5x 2 b) Xác định parabol 2
(P) : y ax bx c, biết rằng nó đi qua (
A 3; 0), B(4;3) và có đỉnh I (2; 1).
Câu 3. (2.0 điểm) Giải các phương trình sau a) 2x 7 x 4; b) x 3 2x 1.
Câu 4. (0.5 điểm) Cho phương trình 2 mx 2m
1 x m 4 0. Tìm m để phương trình có
hai nghiệm phân biệt x , x sao cho 2 2 x x 15. 1 2 1 2
Câu 5. (0.5 điểm) Tìm giá trị nhỏ nhất của hàm số 9 f (x) x với x 2. x 2
Câu 6. (2.5 điểm) Trong mặt phẳng (Oxy), cho ba điểm (
A 1; 2), B(1; 1),C(4; 1) . a) Chứng minh rằng A BC vuông tại B; b) Tính diện tích của A BC;
c) Tìm tọa độ trọng tâm G của A BC.
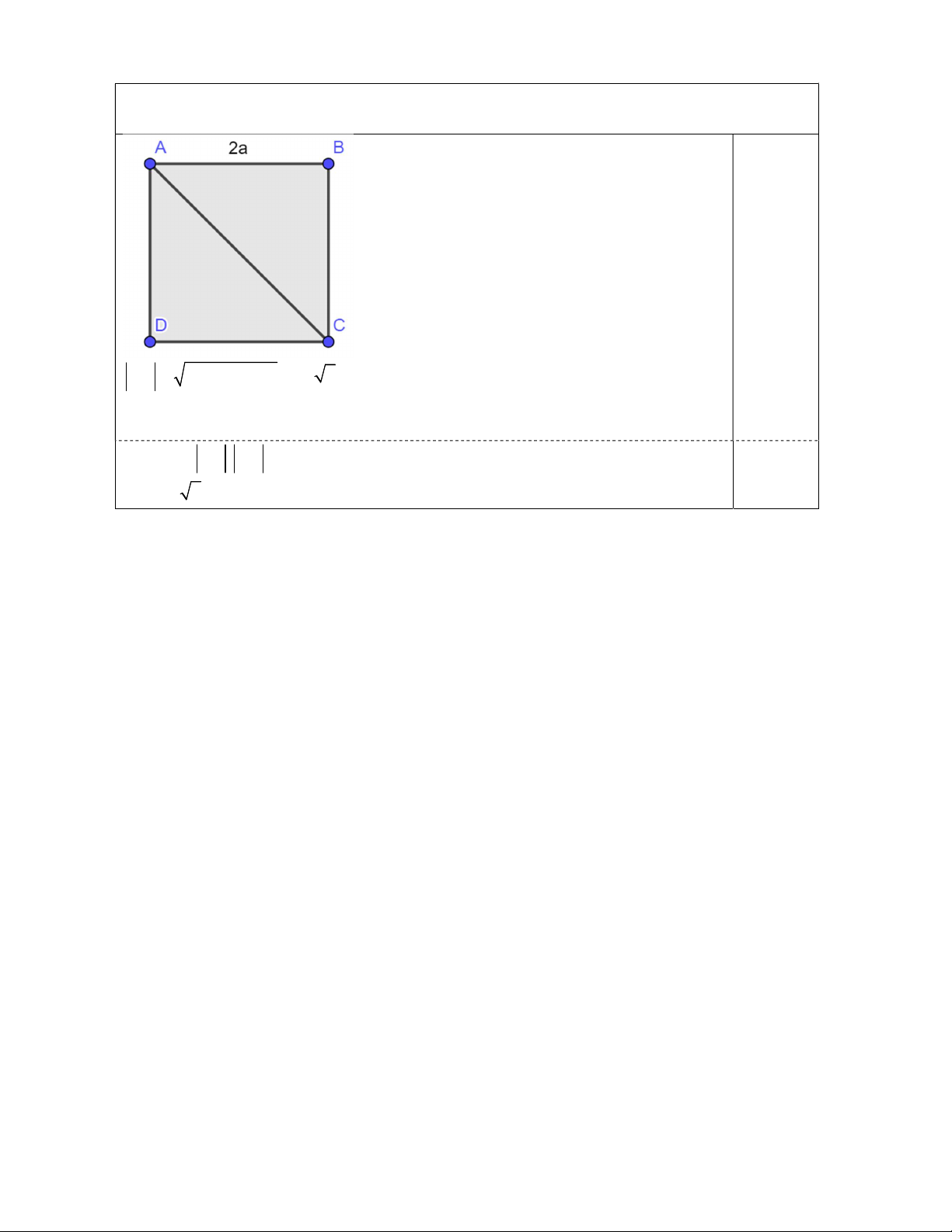
Câu 7. (1.0 điểm) Cho hình vuông ABCD có cạnh bằng 2 . a Hãy tính AC.AD . -------Hết--------
- Học sinh không được sử dụng tài liệu;
- Giám thị coi thi không giải thích gì thêm. HƯỚNG DẪN CHẤM BÀI Gợi ý đáp án Điểm
Câu 1. (2.0 điểm) Cho A (2;3) và B (0;6), xác định A B, A B, A \ B,C A và biểu
diễn chúng trên trục số. 0.25 0 3 A B 0;3 0.25 0.25 0 6 A B 0;6 0.25 0.25 -2 0 A \ B (2;0] 0.25 0.25 ]////////////////[ -2 3 C A ( ; 2 ][3;) 0.25 R
+ Trục số hoặc ghi đáp án có một lỗi sai: -0.25 đ
+ Thiếu hai trong số các lỗi sau thì -0.25đ, thiếu một thì khuyến khích không trừ: âm vô
cùng, dương vô cùng, chia đơn vị không đều, … Câu 2. (1.5 điểm)
a) Tìm tập xác định của hàm số 3x 1 y ; 5x 2 b) Xác định parabol 2
y ax bx c biết rằng nó đi qua (
A 3;0), B(4;3) và có đỉnh I (2;1). a) Điều kiện: 2 0.25 5x 2 0 x 5 Vậy 5 D R \ 2 0.25
b) Vì (P) đi qua A(3;0). B(4;3) và có đỉnh I(2;-1) nên ta có hệ phương trình 2 0 . a 3 . b 3 c 0.25 2 3 . a 4 . b 4 c 2 1 . a 2 . b 2 c 9 a 3b c 0 1 0.25 6a 4b c 3 4a 2b c 1 0.25 a 1 b 4 0.25 c 3 Vậy (P): 2 y x 4x 3
Câu 3. (2.0 điểm) Giải các phương trình sau a) 2x 7 x 4; b) x 3 2x 1. x 4 0 0.25 a) 2x 7 = x 4 2x 7 x 42 x 4 0.25 2 x 10x 9 0 x 4 0.25 x 1(l) x 9(n) Vậy S={9} 0.25 b) |x + 3 = 2x + 1 2x 1 0 x 3 2x 1 0.25 x 3 2x 1 1 x 2 0.25 x 2x 3 1 x 2x 31 1 x 2 0.25 x 2(n) 4 x (l) 5 0.25 Vậy S={2}
Câu 4. (0.5 điểm) Cho phương trình 2 mx 2m
1 x m 4 0. Tìm m để phương trình
có hai nghiệm phân biệt x , x sao cho 2 2 x x 15. 1 2 1 2 m 0
Phương trình có hai nghiệm phân biệt 1 7 0.25 m 4
x x 15 x x 2 2 2 2x x 15 0 1 2 1 2 1 2 2 2m 11m 9 0 m 1(n) 0.25 9 m (n) 2 Vậy 9
m {1; } thì thỏa yêu cầu bài toán 2
Thiếu kết luận không bị trừ điểm
Câu 5. (0.5 điểm) Tìm giá trị nhỏ nhất của hàm số 9 f (x) x với x 2. x 2 Ta có: 9 9 y x x 2 2 x 2 x 2 Vì x > 2 nên 9 x 2 0, 0 x 2
Áp dụng bất đẳng thức Cosi ta được 9 9 x 2 2 2 x 2. 2 8 x 2 x 2 y 8 0.25 9 x n
Dấu “=” xảy ra khi và chỉ khi x 2 x 22 5( ) 9 x 2 x 1 (l)
Vậy với x > 2 thì giá trị nhỏ nhất của hàm số là 8 khi x = 5 0.25
Thiếu trường hợp dấu “=” xảy ra thì bị trừ 0.25 điểm
Câu 6. (2.5 điểm) Trong mặt phẳng (Oxy), cho ba điểm (
A 1; 2), B(1; 1),C(4; 1) . a) Chứng minh rằng A BC vuông tại B; b) Tính diện tích của A BC;
c) Tìm tọa độ trọng tâm G của A BC. a) AB AB 3 AC AC 34 0.5 BC BC 5 Xét A BC ta có 2 2 AB BC 34 2 AC 34 2 2 2
AB BC AC (thỏa định lý Pytago đảo) 0.25 A BC vuông tại B 0.25 b) 1 S B . A BC 0.5 ABC 2 1 15 .3.5 (đvdt) 0.5 2 2
c) Gọi G là trọng tâm của A BC x x x A B C x G 3 0.25 y y y A B C y G 3 2 x G 3 y 0 G 0.25 Vậy 2 G ;0 . 3
Câu 7. (1.0 điểm) Cho hình vuông ABCD cạnh bằng 2 , a tâm . O Hãy tính AC.AD . 2 2 AC (2a) (2a) 2a 2 0.25 AC, AD CAD 45 0.25
AC.AD AC . AD .cos AC, AD 0.25 2 . a 2a 2.cos 45 2 4a 0.25
Các cách giải khác nếu đúng (trong phạm vi chương trình học) vẫn được số điểm tối đa tương ứng.




