Đề thi HK1 Toán 12 năm 2019 – 2020 trường THPT Trần Phú – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 1 môn Giới Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Lan Tường
SỞ GIÁO DỤC & ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT TRẦN PHÚ
ĐỀ CHÍNH THỨC
(Đề có 4 trang)
KỲ KIỂM TRA HỌC KỲ I
L
ỚP 12 − NĂM HỌC 2019
– 2020
Môn thi : Toán
Thời gian làm bài: 90 phút;
(không kể thời gian phát đề)
Mã đề thi 153
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Tìm m để hàm số
4 2
2( 1) 2
y mx m x
(m là tham số) có hai cực tiểu và một cực đại.
A. 0 < m < 1 B. 1 < m < 2 C. m < 0 D. m > 2
Câu 2: Tập xác định của hàm số
ln(ln )
y x
là :
A.
(0; )
B.
C.
(1: )
D.
0;
Câu 3: Gọi
1 2
,
x x
là nghiệm của phương trình:
4
2
log log 64.log 4 0
x x
. Tính giá trị của biểu thức
1 2
log log
A x x
.
A.
4
A
B.
3
A
C.
3
A
D.
2
A
Câu 4: Đạo hàm của hàm số
x x
x x
e e
y
e e
bằng :
A.
2 2
2
2( )
( )
x x
x x
e e
e e
B.
2
4
( )
x x
e e
C.
2
5
( )
x x
e e
D.
x x
e e
Câu 5: Đồ thị hàm số
2
2
9
3 4
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 2 B. 3 C. 1 D. 4
Câu 6: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên. Tìm
khẳng định đúng trong các khẳng định sau :
A. a < b < 0 B. 0 < a < b
C. 0 < b < a D. b < 0 < a
Câu 7: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
4;0
. Tính M + m.
A. M + m = 24 B. M + m =22 C. M + m = 29 D. M + m = 21
Câu 8: Trong các hàm số sau đây, hàm số nào nghịch biến trên R?
A.
4 2
4 5
y x x
B.
3 2
2 7 1
y x x x
C.
3 2
4 cos
y x x x
D.
3 2
4
2 5
3
y x x x
Câu 9: Giải bất phương trình:
2
2 2 8
2 3 2 3
x x x
ta được bao nhiêu nghiệm nguyên ?
A. 5 B. Vô sô C. 6 D. 4
Câu 10: Hàm số
4 3 2
1 1 1
2
4 3 2
y x x x x
có bao nhiêu điểm cực trị ?
A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm
Câu 11: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 60
0
. Thể tích của khối lăng trụ ABC.A’B’C’ bằng :
A.
3
3
2
a
B.
3
3
a
C.
3
3
3
a
D.
3
2
2
a
Câu 12: Cho hàm số
2
1
x
y
x
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường
thẳng (d) :
3 2
y x
.
A. 0 B. 3 C. 2 D. 1
Câu 13: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ?
A. Hàm số
2019
x
y e
đồng biến trên R. B.
log log 2
a
b
e e
.
C. log(ab) = loga + logb D.
ln 0
a
b
Câu 14: Phương trình:
2 1
3 4.3 1 0
x x
có 2 nghiệm
1 2
,
x x
trong đó
1 2
x x
. Khẳng định nào dưới
đây là đúng ?
A.
1 2
2 0
x x
B.
1 2
2 1
x x
C.
1 2
. 1
x x
D.
1 2
2
x x
Câu 15: Cho hàm số
2
2
1
3
x x
y
. Tìm mệnh đề đúng trong các mệnh đề sau sau :
A. Hàm số nghịch biến trên khoảng
(1; )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng
(1; )
D. Hàm số đồng biến trên R.
Câu 16: Một khối gỗ hình lập phương có thể tích bằng
1
V
. Người thợ mộc gọt giũa khối gỗ đó thành một
khối trụ có thể tích bằng
2
V
. Đặt
2
1
V
k
V
. Giá trị lớn nhất của k là :
A.
max
3
k
B.
max
4
k
C.
max
1
4
k
D.
max
2
k
Câu 17: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD =
13
2
a
. Gọi H là
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là :
A.
3
3
a
B.
3
12
a
C.
3
2
3
a
D.
3
2
3
a
Câu 18: Đạo hàm của hàm số
2
ln
x
y
x
bằng :
A.
2
2
2 ln ln
x x x
x
B.
2
2
2 ln
x
x
C.
2
2
2ln ln
x x
x
D.
2
2
2ln ln
x x
x
Câu 19: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm)
A. 8 năm B. 9 năm C. 10 năm D. 11 năm
Câu 20: Tập nghiệm S của bất phương trình:
3 1
3
log log 0
x
là :
A.
1
0;
3
S
B.
1
;
3
S
C. S
D.
(0;1)
S
Câu 21: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA =
3
a
và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là :
A.
2
a
B.
2
6
a
C.
3
2
a
D.
2
4
a
Câu 22: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là :
A.
2
7
2
a
S
B.
2
7
3
a
S
C.
2
7
S a
D.
2
7
6
a
S
Câu 23: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là :
A.
2 57
19
a
B.
2 3
7
a
C.
2
3
a
D.
2 51
17
a
Câu 24: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất.
A. x = 3m B. x = 4m
C. x = 2m D. x = 1,5m
Câu 25: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 60
0
. Bán kính R c
ủa mặt cầu
ngoại tiếp hình chóp S.ABCD đó là :
A.
5
3
a
R
B.
6
2
a
R
C.
3
2
a
R
D.
6
3
a
R
Câu 26: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng
2
5
3
a
. Khi đó thể tích của
hình nón bằng :
A.
3
4
9
a
B.
3
5
9
a
C.
3
2
9
a
D.
3
3
a
Câu 27: Cho hàm số
2
1
2 9
x
y
x mx
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị
của hàm số đã cho có đúng một đường tiệm cận đứng ?
A. 4 B. 1 C. 2 D. 3
Câu 28: Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên. Hàm số
(1 cos )
y f x
đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây :
A. M + 2.m = 5 B. M + 2.m = 1
C. 2.M + m = 6 D.
2 2
9
M m
Câu 29: Cho hàm số
( )
y f x
liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình
( ) 2
f f x
có bao nhiêu nghiệm ?
A. 4 B. 6
C. 5 D. 3
Câu 30: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là :
A.
2
1
2
3
a
B.
2
1
3
3
a
C.
2
3
a
D.
2
1
3
2
a
PHẦN II : TỰ LUẬN (4 điểm − 25 phút)
--------------
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số
3 2
1
( 6) 2 1
3
y x mx m x m
có cực đại và
cực tiểu.
Bài 2: (1điềm) Cho hàm số
2 1
2
x
y
x
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có
hoành độ
1
M
x
.
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
.
Bài 4: (1 điểm) Giải bất phương trình:
5
1
5
log ( 4) 1 log
x x
.
-----------------------------------------------
----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT TRẦN PHÚ
ĐỀ CHÍNH THỨC
(Đề có 4 trang)
KỲ KIỂM TRA HỌC KỲ I
L
ỚP 12 − NĂM HỌC 2019
– 2020
Môn thi : Toán
Thời gian làm bài: 90 phút;
(không kể thời gian phát đề)
Mã đề thi 151
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Tập nghiệm S của bất phương trình:
3 1
3
log log 0
x
là :
A.
(0;1)
S
B.
1
;
3
S
C. S
D.
1
0;
3
S
Câu 2: Tập xác định của hàm số
ln(ln )
y x
là :
A.
0;
B.
(1: )
C.
D.
(0; )
Câu 3: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD =
13
2
a
. Gọi H là
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là :
A.
3
3
a
B.
3
2
3
a
C.
3
2
3
a
D.
3
12
a
Câu 4: Giải bất phương trình:
2
2 2 8
2 3 2 3
x x x
ta được bao nhiêu nghiệm nguyên ?
A. 4 B. 5 C. 6 D. Vô số
Câu 5: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm)
A. 10 năm B. 9 năm C. 8 năm D. 11 năm
Câu 6: Một khối gỗ hình lập phương có thể tích bằng
1
V
. Người thợ mộc gọt giũa khối gỗ đó thành một
khối trụ có thể tích bằng
2
V
. Đặt
2
1
V
k
V
. Giá trị lớn nhất của k là :
A.
max
3
k
B.
max
2
k
C.
max
4
k
D.
max
1
4
k
Câu 7: Tìm m để hàm số
4 2
2( 1) 2
y mx m x
(m là tham số) có hai cực tiểu và một cực đại.
A. 0 < m < 1 B. m < 0 C. m > 2 D. 1 < m < 2
Câu 8: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên. Tìm
khẳng định đúng trong các khẳng định sau :
A. b < 0 < a B. 0 < a < b
C. 0 < b < a D. a < b < 0
Câu 9: Cho hàm số
2
1
x
y
x
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường
thẳng (d) :
3 2
y x
.
A. 0 B. 3 C. 2 D. 1
Câu 10: Đạo hàm của hàm số
2
ln
x
y
x
bằng :
A.
2
2
2 ln ln
x x x
x
B.
2
2
2 ln
x
x
C.
2
2
2ln ln
x x
x
D.
2
2
2ln ln
x x
x
Câu 11: Phương trình:
2 1
3 4.3 1 0
x x
có 2 nghiệm
1 2
,
x x
trong đó
1 2
x x
. Khẳng định nào dưới
đây là đúng ?
A.
1 2
. 1
x x
B.
1 2
2 0
x x
C.
1 2
2 1
x x
D.
1 2
2
x x
Câu 12: Trong các hàm số sau đây, hàm số nào nghịch biến trên R?
A.
4 2
4 5
y x x
B.
3 2
4 cos
y x x x
C.
3 2
4
2 5
3
y x x x
D.
3 2
2 7 1
y x x x
Câu 13: Hàm số
4 3 2
1 1 1
2
4 3 2
y x x x x
có bao nhiêu điểm cực trị ?
A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm
Câu 14: Đồ thị hàm số
2
2
9
3 4
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 2 B. 1 C. 4 D. 3
Câu 15: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
4;0
. Tính M + m.
A. M + m = 22 B. M + m = 24 C. M + m = 21 D. M + m = 29
Câu 16: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 60
0
. Thể tích của khối lăng trụ ABC.A’B’C’ bằng :
A.
3
3
2
a
B.
3
3
a
C.
3
3
3
a
D.
3
2
2
a
Câu 17: Cho hàm số
2
2
1
3
x x
y
. Tìm mệnh đề đúng trong các mệnh đề sau sau :
A. Hàm số nghịch biến trên khoảng
(1; )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng
(1; )
D. Hàm số đồng biến trên R.
Câu 18: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ?
A. Hàm số
2019
x
y e
đồng biến trên R. B.
log log 2
a
b
e e
.
C. log(ab) = loga + logb D.
ln 0
a
b
Câu 19: Gọi
1 2
,
x x
là nghiệm của phương trình:
4
2
log log 64.log 4 0
x x
. Tính giá trị của biểu thức
1 2
log log
A x x
.
A.
3
A
B.
3
A
C.
2
A
D.
4
A
Câu 20: Đạo hàm của hàm số
x x
x x
e e
y
e e
bằng :
A.
2
5
( )
x x
e e
B.
2
4
( )
x x
e e
C.
x x
e e
D.
2 2
2
2( )
( )
x x
x x
e e
e e
Câu 21: Cho hàm số
2
1
2 9
x
y
x mx
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị
của hàm số đã cho có đúng một đường tiệm cận đứng ?
A. 2 B. 3 C. 1 D. 4
Câu 22: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là :
A.
2
7
2
a
S
B.
2
7
6
a
S
C.
2
7
S a
D.
2
7
3
a
S
Câu 23: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 60
0
. Bán kính R c
ủa mặt cầu
ngoại tiếp hình chóp S.ABCD đó là :
A.
6
2
a
R
B.
6
3
a
R
C.
3
2
a
R
D.
5
3
a
R
Câu 24: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng
2
5
3
a
. Khi đó thể tích của
hình nón bằng :
A.
3
4
9
a
B.
3
5
9
a
C.
3
2
9
a
D.
3
3
a
Câu 25: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là :
A.
2
1
2
3
a
B.
2
3
a
C.
2
1
3
2
a
D.
2
1
3
3
a
Câu 26: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA =
3
a
và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là :
A.
2
a
B.
2
4
a
C.
3
2
a
D.
2
6
a
Câu 27: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là :
A.
2 57
19
a
B.
2
3
a
C.
2 3
7
a
D.
2 51
17
a
Câu 28: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất.
A. x = 3m B. x = 4m
C. x = 2m D. x = 1,5m
Câu 29: Cho hàm số
( )
y f x
liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình
( ) 2
f f x
có bao nhiêu nghiệm ?
A. 3 B. 4
C. 5 D. 6
Câu 30: Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên. Hàm số
(1 cos )
y f x
đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây :
A. M + 2.m = 1 B. M + 2.m = 5
C.
2 2
9
M m
D. 2.M + m = 6
PHẦN II : TỰ LUẬN (4 điểm − 25 phút)
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số
3 2
1
( 6) 2 1
3
y x mx m x m
có cực đại và
cực tiểu.
Bài 2: (1điềm) Cho hàm số
2 1
2
x
y
x
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có
hoành độ
1
M
x
.
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
.
Bài 4: (1 điểm) Giải bất phương trình :
5
1
5
log ( 4) 1 log
x x
.
-----------------------------------------
----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT TRẦN PHÚ
ĐỀ CHÍNH THỨC
(Đề có 4 trang)
KỲ KIỂM TRA HỌC KỲ I
L
ỚP 12 − NĂM HỌC 2019
– 2020
Môn thi : Toán
Thời gian làm bài: 90 phút;
(không kể thời gian phát đề)
Mã đề thi 152
PH
ẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm)
A. 10 năm B. 8 năm C. 9 năm D. 11 năm
Câu 2: Cho hàm số
2
1
x
y
x
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường
thẳng (d) :
3 2
y x
.
A. 1 B. 3 C. 2 D. 0
Câu 3: Đạo hàm của hàm số
x x
x x
e e
y
e e
bằng :
A.
2
5
( )
x x
e e
B.
2
4
( )
x x
e e
C.
x x
e e
D.
2 2
2
2( )
( )
x x
x x
e e
e e
Câu 4: Phương trình:
2 1
3 4.3 1 0
x x
có 2 nghiệm
1 2
,
x x
trong đó
1 2
x x
. Khẳng định nào dưới đây
là đúng ?
A.
1 2
2 0
x x
B.
1 2
. 1
x x
C.
1 2
2
x x
D.
1 2
2 1
x x
Câu 5: Trong các hàm số sau đây, hàm số nào nghịch biến trên R?
A.
3 2
4 cos
y x x x
B.
3 2
2 7 1
y x x x
C.
3 2
4
2 5
3
y x x x
D.
4 2
4 5
y x x
Câu 6: Gọi
1 2
,
x x
là nghiệm của phương trình:
4
2
log log 64.log 4 0
x x
. Tính giá trị của biểu thức
1 2
log log
A x x
.
A.
3
A
B.
3
A
C.
2
A
D.
4
A
Câu 7: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên. Tìm
khẳng định đúng trong các khẳng định sau :
A. a < b < 0 B. 0 < a < b
C. 0 < b < a D. b < 0 < a
Câu 8: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
4;0
. Tính M + m.
A. M + m = 24 B. M + m = 22 C. M + m = 29 D. M + m = 21
Câu 9: Tập xác định của hàm số
ln(ln )
y x
là :
A.
(0;1)
B.
(0; )
C.
0;
D.
(1: )
Câu 10: Tập nghiệm S của bất phương trình:
3 1
3
log log 0
x
là :
A.
(0;1)
S
B.
1
0;
3
S
C.
1
;
3
S
D.
S
Câu 11: Đồ thị hàm số
2
2
9
3 4
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 4 B. 1 C. 2 D. 3
Câu 12: Hàm số
4 3 2
1 1 1
2
4 3 2
y x x x x
có bao nhiêu điểm cực trị ?
A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm
Câu 13: Giải bất phương trình:
2
2 2 8
2 3 2 3
x x x
ta được bao nhiêu nghiệm nguyên ?
A. 5 B. Vô sô C. 6 D. 4
Câu 14: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ?
A. Hàm số
2019
x
y e
đồng biến trên R. B.
log log 2
a
b
e e
.
C. log(ab) = loga + logb D.
ln 0
a
b
Câu 15: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 60
0
. Thể tích của khối lăng trụ ABC.A’B’C’ bằng :
A.
3
3
2
a
B.
3
3
a
C.
3
3
3
a
D.
3
2
2
a
Câu 16: Cho hàm số
2
2
1
3
x x
y
. Tìm mệnh đề đúng trong các mệnh đề sau sau :
A. Hàm số nghịch biến trên khoảng
(1; )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng
(1; )
D. Hàm số đồng biến trên R.
Câu 17: Một khối gỗ hình lập phương có thể tích bằng
1
V
. Người thợ mộc gọt giũa khối gỗ đó thành một
khối trụ có thể tích bằng
2
V
. Đặt
2
1
V
k
V
. Giá trị lớn nhất của k là :
A.
max
3
k
B.
max
4
k
C.
max
1
4
k
D.
max
2
k
Câu 18: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD =
13
2
a
. Gọi H là
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là :
A.
3
3
a
B.
3
12
a
C.
3
2
3
a
D.
3
2
3
a
Câu 19: Đạo hàm của hàm số
2
ln
x
y
x
bằng :
A.
2
2
2 ln ln
x x x
x
B.
2
2
2 ln
x
x
C.
2
2
2ln ln
x x
x
D.
2
2
2ln ln
x x
x
Câu 20: Tìm m để hàm số
4 2
2( 1) 2
y mx m x
(m là tham số) có hai cực tiểu và một cực đại.
A. 0 < m < 1 B. m < 0 C. m > 2 D. 1 < m < 2
Câu 21: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 60
0
. Bán kính R c
ủa mặt cầu
ngoại tiếp hình chóp S.ABCD đó là :
A.
5
3
a
R
B.
3
2
a
R
C.
6
3
a
R
D.
6
2
a
R
Câu 22: Cho hàm số
( )
y f x
liên tục trên R và có đồ thị như
hình vẽ bên. Hỏi phương trình
( ) 2
f f x
có bao nhiêu
nghiệm ?
A. 5 B. 3
C. 4 D. 6
Câu 23: Cho hàm số
2
1
2 9
x
y
x mx
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị
của hàm số đã cho có đúng một đường tiệm cận đứng ?
A. 3 B. 2 C. 4 D. 1
Câu 24: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là :
A.
2
1
3
2
a
B.
2
1
2
3
a
C.
2
3
a
D.
2
1
3
3
a
Câu 25: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là :
A.
2
7
2
a
S
B.
2
7
3
a
S
C.
2
7
S a
D.
2
7
6
a
S
Câu 26: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là :
A.
2 51
17
a
B.
2
3
a
C.
2 3
7
a
D.
2 57
19
a
Câu 27: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất.
A. x = 3m B. x = 4m
C. x = 2m D. x = 1,5m
Câu 28: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng
2
5
3
a
. Khi đó thể tích của
hình nón bằng :
A.
3
5
9
a
B.
3
4
9
a
C.
3
2
9
a
D.
3
3
a
Câu 29: Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên. Hàm số
(1 cos )
y f x
đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây :
A. M + 2.m = 5 B. M + 2.m = 1
C. 2.M + m = 6 D.
2 2
9
M m
Câu 30: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a .Cạnh SA =
3
a
và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là :
A.
2
a
B.
2
4
a
C.
2
6
a
D.
3
2
a
PHẦN II : TỰ LUẬN (4 điểm − 25 phút)
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số
3 2
1
( 6) 2 1
3
y x mx m x m
có cực đại và
cực tiểu.
Bài 2: (1điềm) Cho hàm số
2 1
2
x
y
x
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có
hoành độ
1
M
x
.
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
.
Bài 4: (1 điểm) Giải bất phương trình :
5
1
5
log ( 4) 1 log
x x
.
----------------------
----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT TRẦN PHÚ
ĐỀ CHÍNH THỨC
(Đề có 4 trang)
KỲ KIỂM TRA HỌC KỲ I
L
ỚP 12 − NĂM HỌC 2019
– 2020
Môn thi : Toán
Thời gian làm bài: 90 phút;
(không kể thời gian phát đề)
Mã đề thi 154
PH
ẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD =
13
2
a
. Gọi H là
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là :
A.
3
3
a
B.
3
12
a
C.
3
2
3
a
D.
3
2
3
a
Câu 2: Phương trình:
2 1
3 4.3 1 0
x x
có 2 nghiệm
1 2
,
x x
trong đó
1 2
x x
. Khẳng định nào dưới đây
là đúng ?
A.
1 2
2 0
x x
B.
1 2
. 1
x x
C.
1 2
2 1
x x
D.
1 2
2
x x
Câu 3: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 60
0
. Thể tích của khối lăng trụ ABC.A’B’C’ bằng :
A.
3
3
2
a
B.
3
3
a
C.
3
3
3
a
D.
3
2
2
a
Câu 4: Một khối gỗ hình lập phương có thể tích bằng
1
V
. Người thợ mộc gọt giũa khối gỗ đó thành một
khối trụ có thể tích bằng
2
V
. Đặt
2
1
V
k
V
. Giá trị lớn nhất của k là :
A.
max
3
k
B.
max
4
k
C.
max
1
4
k
D.
max
2
k
Câu 5: Cho hàm số
2
2
1
3
x x
y
. Tìm mệnh đề đúng trong các mệnh đề sau sau :
A. Hàm số nghịch biến trên khoảng
(1; )
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên R D. Hàm số đồng biến trên khoảng
(1; )
Câu 6: Đạo hàm của hàm số
2
ln
x
y
x
bằng :
A.
2
2
2 ln ln
x x x
x
B.
2
2
2 ln
x
x
C.
2
2
2ln ln
x x
x
D.
2
2
2ln ln
x x
x
Câu 7: Trong các hàm số sau đây, hàm số nào nghịch biến trên R?
A.
4 2
4 5
y x x
B.
3 2
2 7 1
y x x x
C.
3 2
4 cos
y x x x
D.
3 2
4
2 5
3
y x x x
Câu 8: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
3 2
3 9 1
y x x x
trên đoạn
4;0
. Tính M + m.
A. M + m = 21 B. M + m = 29 C. M + m = 24 D. M + m = 22
Câu 9: Hàm số
4 3 2
1 1 1
2
4 3 2
y x x x x
có bao nhiêu điểm cực trị ?
A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm
Câu 10: Cho hàm số
2
1
x
y
x
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường
thẳng (d) :
3 2
y x
.
A. 2 B. 3 C. 0 D. 1
Câu 11: Đạo hàm của hàm số
x x
x x
e e
y
e e
bằng :
A.
2
5
( )
x x
e e
B.
2 2
2
2( )
( )
x x
x x
e e
e e
C.
2
4
( )
x x
e e
D.
x x
e e
Câu 12: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ?
A. Hàm số
2019
x
y e
đồng biến trên R. B. log(ab) = loga + logb
C.
ln 0
a
b
D.
log log 2
a
b
e e
.
Câu 13: Đồ thị hàm số
2
2
9
3 4
x
y
x x
có bao nhiêu đường tiệm cận ?
A. 3 B. 4 C. 1 D. 2
Câu 14: Gọi
1 2
,
x x
là nghiệm của phương trình:
4
2
log log 64.log 4 0
x x
. Tính giá trị của biểu thức
1 2
log log
A x x
.
A.
4
A
B.
3
A
C.
3
A
D.
2
A
Câu 15: Giải bất phương trình:
2
2 2 8
2 3 2 3
x x x
ta được bao nhiêu nghiệm nguyên ?
A. 5 B. 6 C. 4 D. Vô sô
Câu 16: Tập xác định của hàm số
ln(ln )
y x
là :
A.
0;
B.
(1: )
C.
(0;1)
D.
(0; )
Câu 17: Cho hàm số
1
ax b
y
x
có đồ thị như hình vẽ bên. Tìm
khẳng định đúng trong các khẳng định sau :
A. 0 < a < b B. b < 0 < a
C. a < b < 0 D. 0 < b < a
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm)
A. 8 năm B. 9 năm C. 10 năm D. 11 năm
Câu 19: Tập nghiệm S của bất phương trình:
3 1
3
log log 0
x
là :
A.
1
0;
3
S
B.
S
C.
1
;
3
S
D.
(0;1)
S
Câu 20: Tìm m để hàm số
4 2
2( 1) 2
y mx m x
(m là tham số) có hai cực tiểu và một cực đại.
A. 0 < m < 1 B. m < 0 C. 1 < m < 2 D. m > 2
Câu 21: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là :
A.
2
7
2
a
S
B.
2
7
3
a
S
C.
2
7
S a
D.
2
7
6
a
S
Câu 22: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng
2
5
3
a
. Khi đó thể tích của
hình nón bằng :
A.
3
4
9
a
B.
3
5
9
a
C.
3
2
9
a
D.
3
3
a
Câu 23: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA =
3
a
và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là :
A.
2
a
B.
3
2
a
C.
2
4
a
D.
2
6
a
Câu 24: Cho hàm số
( )
y f x
liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình
( ) 2
f f x
có bao nhiêu nghiệm ?
A. 6 B. 3
C. 5 D. 4
Câu 25: Cho hàm số
( )
y f x
có đồ thị như hình vẽ bên. Hàm số
(1 cos )
y f x
đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây :
A.
2 2
9
M m
B. M + 2.m = 1
C. 2.M + m = 6 D. M + 2.m = 5
Câu 26: Cho hàm số
2
1
2 9
x
y
x mx
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị
của hàm số đã cho có đúng một đường tiệm cận đứng ?
A. 4 B. 1 C. 2 D. 3
Câu 27: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là :
A.
2 57
19
a
B.
2 51
17
a
C.
2 3
7
a
D.
2
3
a
Câu 28: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là :
A.
2
1
2
3
a
B.
2
1
3
3
a
C.
2
3
a
D.
2
1
3
2
a
Câu 29: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 60
0
. Bán kính R c
ủa mặt cầu
ngoại tiếp hình chóp S.ABCD đó là :
A.
6
3
a
R
B.
5
3
a
R
C.
6
2
a
R
D.
3
2
a
R
Câu 30: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất.
A. x = 3m B. x = 4m
C. x = 2m D. x = 1,5m
PHẦN II : TỰ LUẬN (4 điểm − 25 phút)
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số
3 2
1
( 6) 2 1
3
y x mx m x m
có cực đại và
cực tiểu.
Bài 2: (1điềm) Cho hàm số
2 1
2
x
y
x
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có
hoành độ
1
M
x
.
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
.
Bài 4: (1 điểm) Giải bất phương trình :
5
1
5
log ( 4) 1 log
x x
.
-----------------------------------------------
----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
KIỂM TRA HỌC KỲ I
TOÁN 12 NH 2019 − 2020
ĐÁP ÁN PHẦN TỰ LUẬN
Bài 1: (1 điêm) Tìm các giá trị của tham số m để
hàm số
3 2
1
( 6) 2 1
3
y x mx m x m
có cực
đại và cực tiểu.
2
' 2 6
y x mx m
0,25đ
Để hàm số có CĐ, CT
PT y’ 0 có 2 nghiệm phân biệt
0
' 0
a
0,25đ
2
6 0
m m
0,25đ
2
3
m
m
0,25đ
Bài 2: (1điềm) Cho hàm số
2 1
2
x
y
x
có đồ thị
(C). Viết phương trình tiếp tuyến tại điểm M thuộc
(C) có hoành độ
1
M
x
.
2
5
'
( 2)
y
x
0,25đ
y’(1) 5 0,25đ
1
M
x
3
M
y
0,25đ
PTTT : y 5x − 2 0,25đ
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ
nhất của hàm số
2
x
x
y
e
trên đoạn
1;1
.
2
2
'
x
x x
y
e
0,25đ
y’ 0
2
0 ( )
2 0
2 ( )
x n
x x
x loai
0,25đ
Ta có :
( 1)
f e
(0) 0
f
1
(1)f
e
Vậy :
1;1
min 0
y
;
1;1
max
y e
0,5đ
Bài 4: (1 điểm) Giải bất phương trình:
5
1
5
log ( 4) 1 log
x x
.
ĐK : x > 0 0,25đ
4 1
5
x
BPT
x
0,25đ
2
4 5 0
x x
5 1
x
0,25đ
So với đk trên, nghiệm BPT là :
0 < x 1 0,25đ
TRƯỜNG THPT TRẦN PHÚ
KIỂM TRA HỌC KỲ 1 NĂM HỌC 2019 - 2020
ĐÁP ÁN TR
ẮC NGHIỆM TOÁN KHỐI 12 (CHỈNH SỬA)
Câu
Mã đề 151
Câu
Mã đề 152
Câu
Mã đề
153
Câu
Mã đề
154
1
D
1
C
1
A
1
D
2
B
2
A
2
C
2
C
3
B
3
B
3
B
3
A
4
C
4
D
4
B
4
B
5
B
5
C
5
C
5
A
6
C
6
B
6
C
6
D
7
A
7
C
7
C
7
D
8
C
8
C
8
D
8
B
9
D
9
D
9
C
9
A
10
D
10
B
10
A
10
D
11
C
11
B
11
A
11
C
12
C
12
A
12
D
12
C
13
A
13
C
13
D
13
C
14
B
14
D
14
B
14
C
15
D
15
A
15
A
15
B
16
A
16
A
16
B
16
B
17
A
17
B
17
D
17
D
18
D
18
D
18
D
18
B
19
A
19
D
19
B
19
A
20
B
20
A
20
A
20
A
21
B
21
C
21
B
21
B
22
D
22
A
22
B
22
A
23
B
23
A
23
A
23
D
24
A
24
D
24
C
24
C
25
D
25
B
25
D
25
B
26
D
26
D
26
A
26
D
2
7
A
27
C
27
D
27
A
28
C
28
B
28
B
28
B
29
C
29
B
29
C
29
A
30
A
30
C
30
B
30
C
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC & ĐÀO TẠO KỲ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH
LỚP 12 − NĂM HỌC 2019 – 2020 TRƯỜNG THPT TRẦN PHÚ Môn thi : Toán
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(không kể thời gian phát đề) (Đề có 4 trang) Mã đề thi 153
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Tìm m để hàm số 4 2
y  mx  2(m 1)x  2 (m là tham số) có hai cực tiểu và một cực đại. A. 0 < m < 1 B. 1 < m < 2 C. m < 0 D. m > 2
Câu 2: Tập xác định của hàm số y  ln(ln x ) là : A. ( 0;   ) B. ( 0;1) C. (1:  ) D. 0; 
Câu 3: Gọi x , x là nghiệm của phương trình: 2
log x  log 64. log x  4  0 . Tính giá trị của biểu thức 1 2 4 A  log  1 x log 2 x . A. A  4 B. A  3  C. A  3 D. A  2 x x e  e
Câu 4: Đạo hàm của hàm số y  bằng : x x e  e 2x 2 2( x e  e ) 4 5 A. B. C. D. x x e e  x x 2 (e  e ) x x 2 (e e  ) x x 2 (e  e ) 2 9  x
Câu 5: Đồ thị hàm số y 
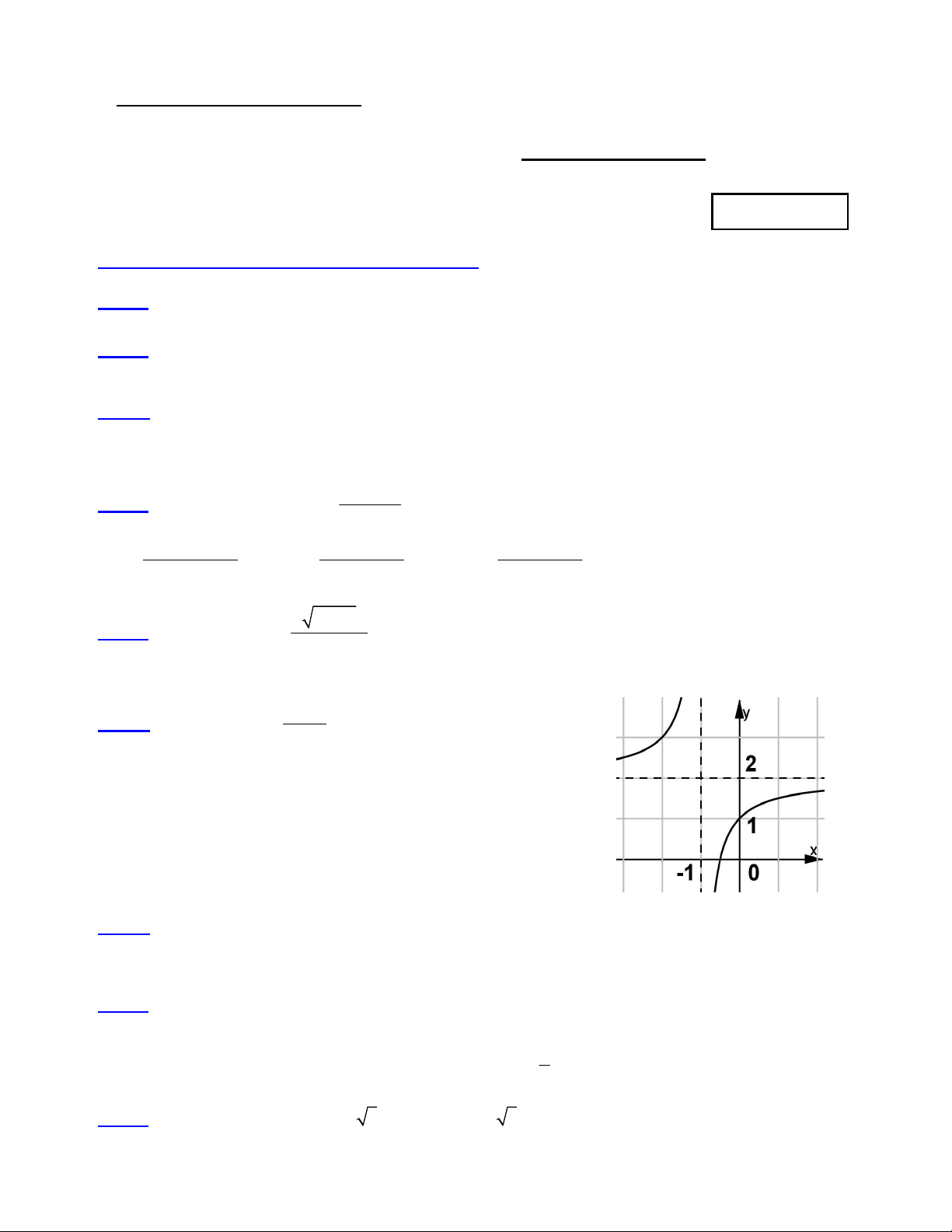
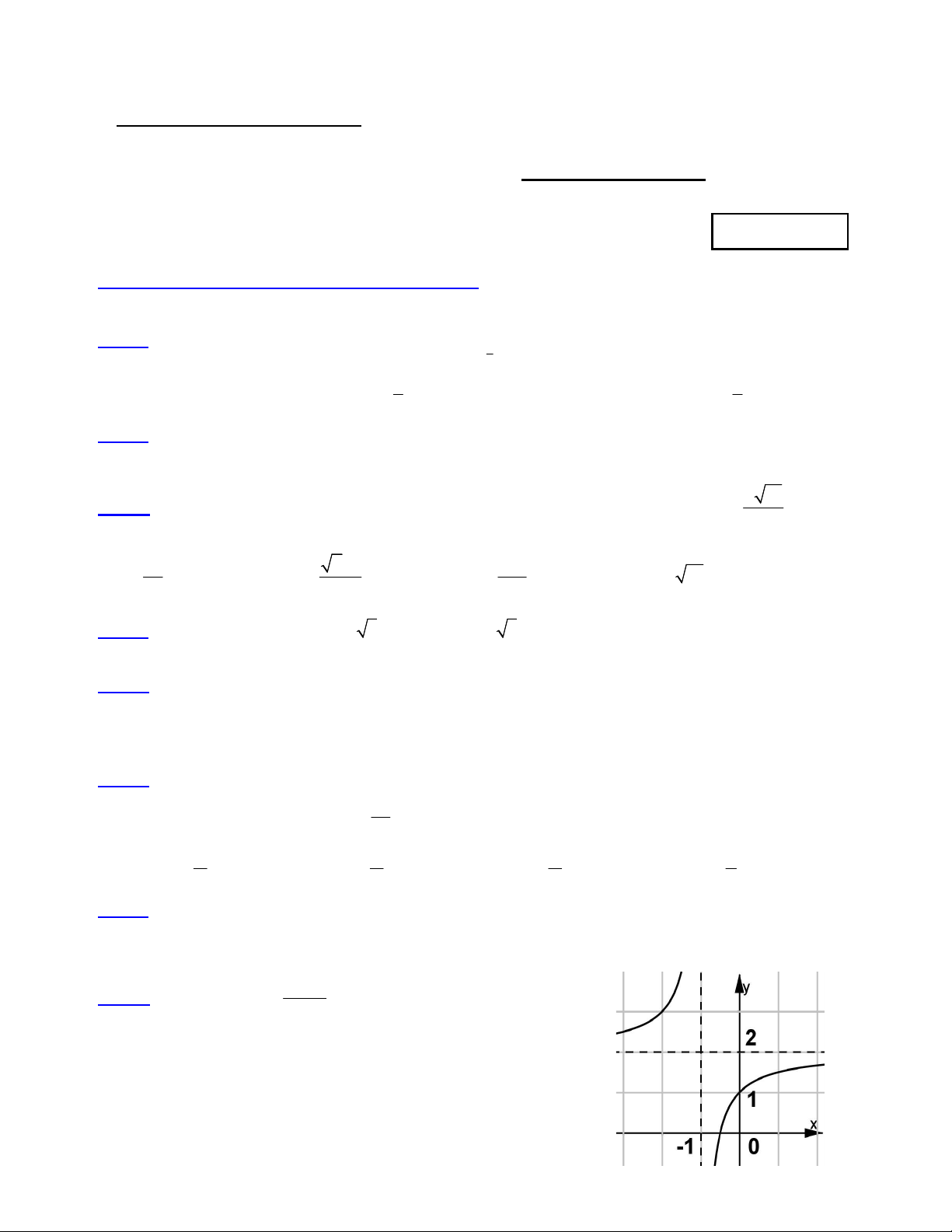
có bao nhiêu đường tiệm cận ? 2 x  3x  4 A. 2 B. 3 C. 1 D. 4 ax  b Câu 6: Cho hàm số y 
có đồ thị như hình vẽ bên. Tìm x 1
khẳng định đúng trong các khẳng định sau : A. a < b < 0 B. 0 < a < b C. 0 < b < a D. b < 0 < a
Câu 7: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  x  3x  9x  1 trên đoạn 4;0. Tính M + m. A. M + m = 24 B. M + m =22 C. M + m = 29 D. M + m = 21
Câu 8: Trong các hàm số sau đây, hàm số nào nghịch biến trên R? A. 4 2 y   x  4x  5 B. 3 2
y   x  2x  7x 1 4 C. 3 2 y  x  4x  cos x D. 3 2
y   x  2x  x  5 3 2 x  2x  2  x  8
Câu 9: Giải bất phương trình: 2  3  2  3
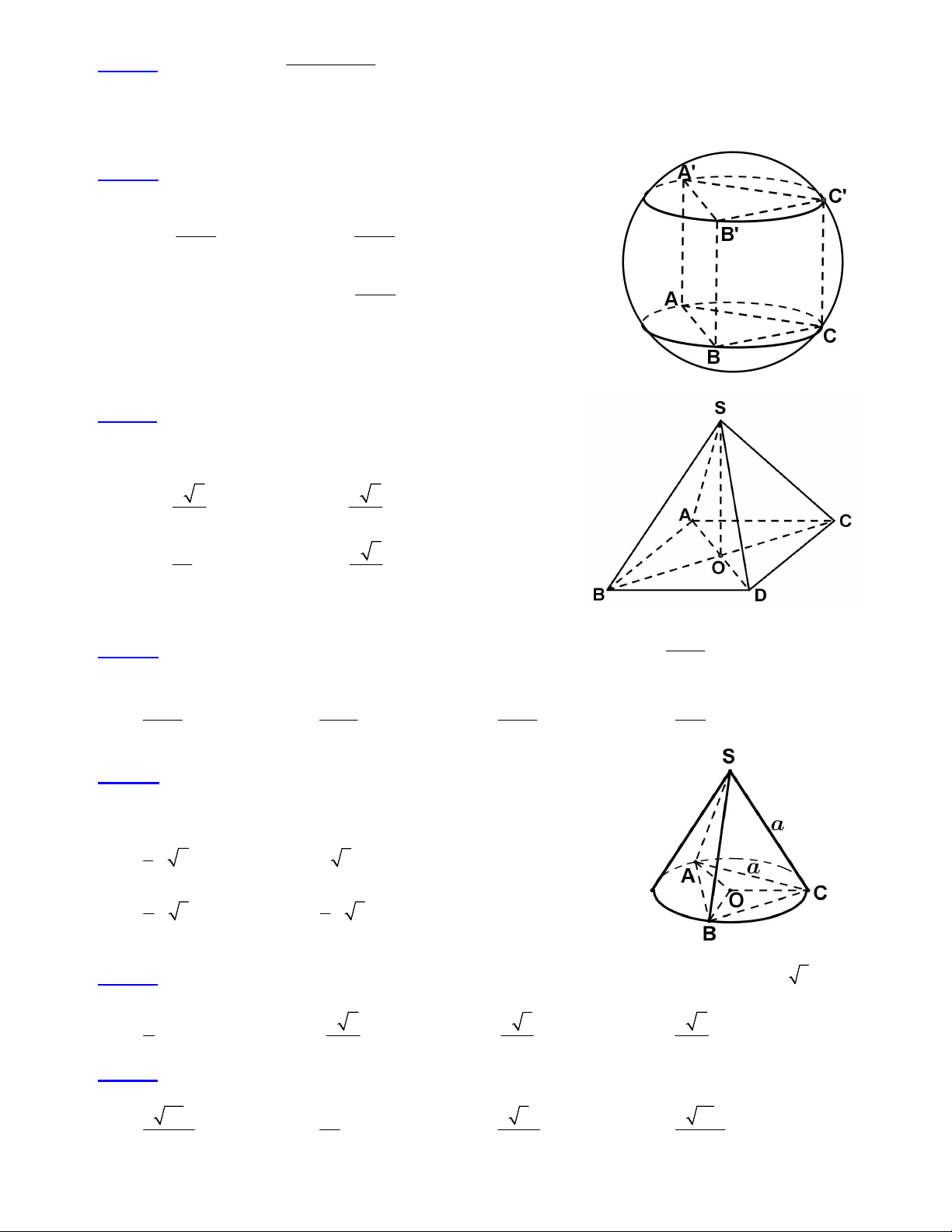
ta được bao nhiêu nghiệm nguyên ? A. 5 B. Vô sô C. 6 D. 4 1 1 1 Câu 10: Hàm số 4 3 2
y  x  x  x  x  2 có bao nhiêu điểm cực trị ? 4 3 2 A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm
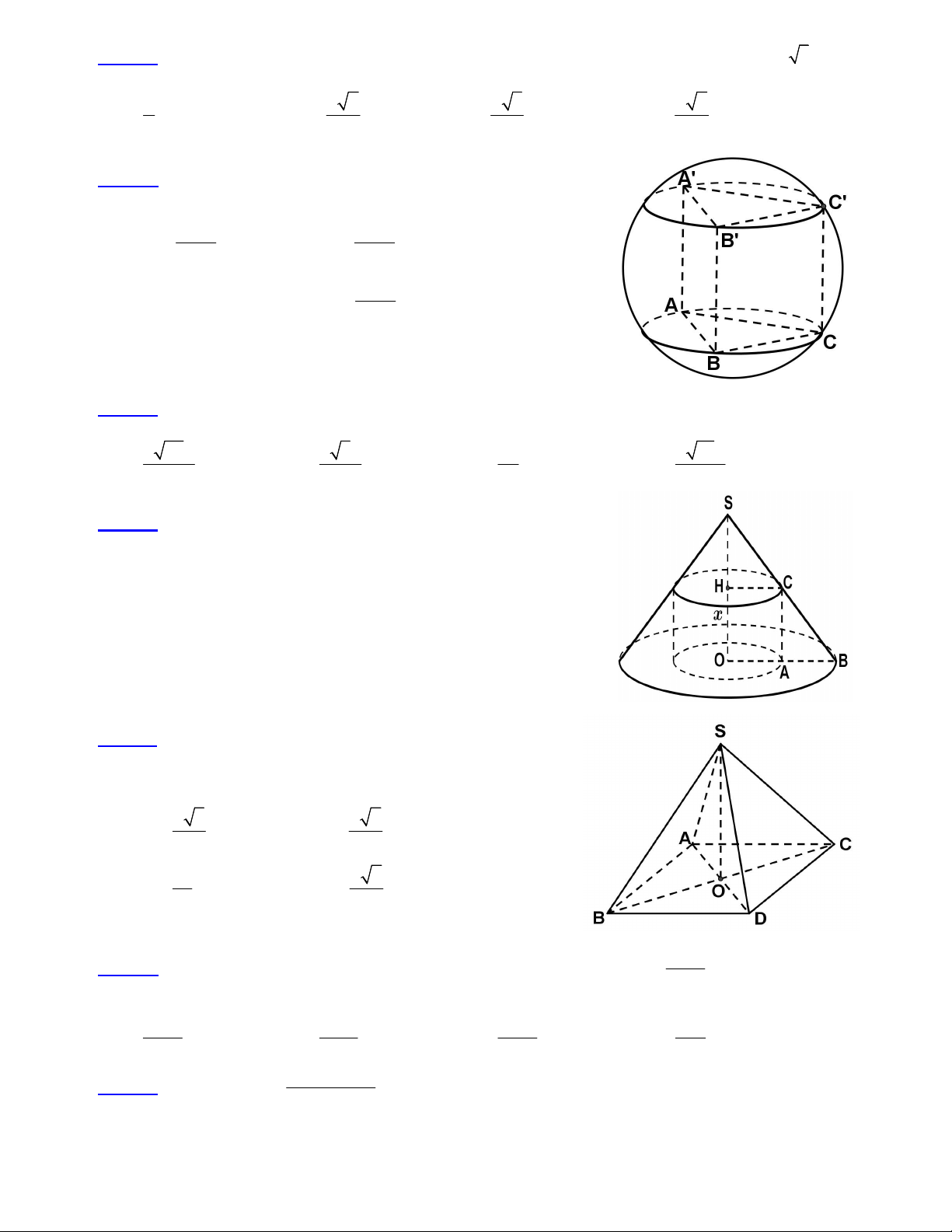
Câu 11: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 600. Thể tích của khối lăng trụ ABC.A’B’C’ bằng : 3 3a 3 3a 3 2 a A. B. 3 3a C. D. 2 3 2 x  2 Câu 12: Cho hàm số y 
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường x 1
thẳng (d) : y  3x  2 . A. 0 B. 3 C. 2 D. 1
Câu 13: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ? A. Hàm số x 2019 y e   đồng biến trên R. B. log e  log e  2 a . b a C. log(ab) = loga + logb D. ln  0 b
Câu 14: Phương trình: 2x 1 3
 4.3x  1  0 có 2 nghiệm 1 x , 2 x trong đó 
. Khẳng định nào dưới 1 x 2 x đây là đúng ? A. 2   C. D. 1 x   B. 2 x 0 1 x  2 2 x 1 1 x . 2 x  1 1 x    2 x 2 2 x  2  1 x 
Câu 15: Cho hàm số y   
. Tìm mệnh đề đúng trong các mệnh đề sau sau :  3 
A. Hàm số nghịch biến trên khoảng (1;   )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng (1;   )
D. Hàm số đồng biến trên R.
Câu 16: Một khối gỗ hình lập phương có thể tích bằng 1
V . Người thợ mộc gọt giũa khối gỗ đó thành một V
khối trụ có thể tích bằng  2 V . Đặt 2 k
. Giá trị lớn nhất của k là : 1 V   1  A. kmax  B. k  C. k  D. k  3 max 4 max 4 max 2 a 13
Câu 17: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD = . Gọi H là 2
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là : 3 a 3 2a 3 2 a A. B. 3 12a C. D. 3 3 3 2 ln x
Câu 18: Đạo hàm của hàm số y  bằng : x 2 2x ln x  ln x 2 2  ln x 2 2ln x  ln x 2 2ln x  ln x A. B. C. D. 2 x 2 x 2 x 2 x
Câu 19: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm) A. 8 năm B. 9 năm C. 10 năm D. 11 năm  
Câu 20: Tập nghiệm S của bất phương trình: log  log x  0 là : 3 1    3  1 1 A. S    0;   B. S    ;   C. S   D. S  ( 0;1)  3   3 
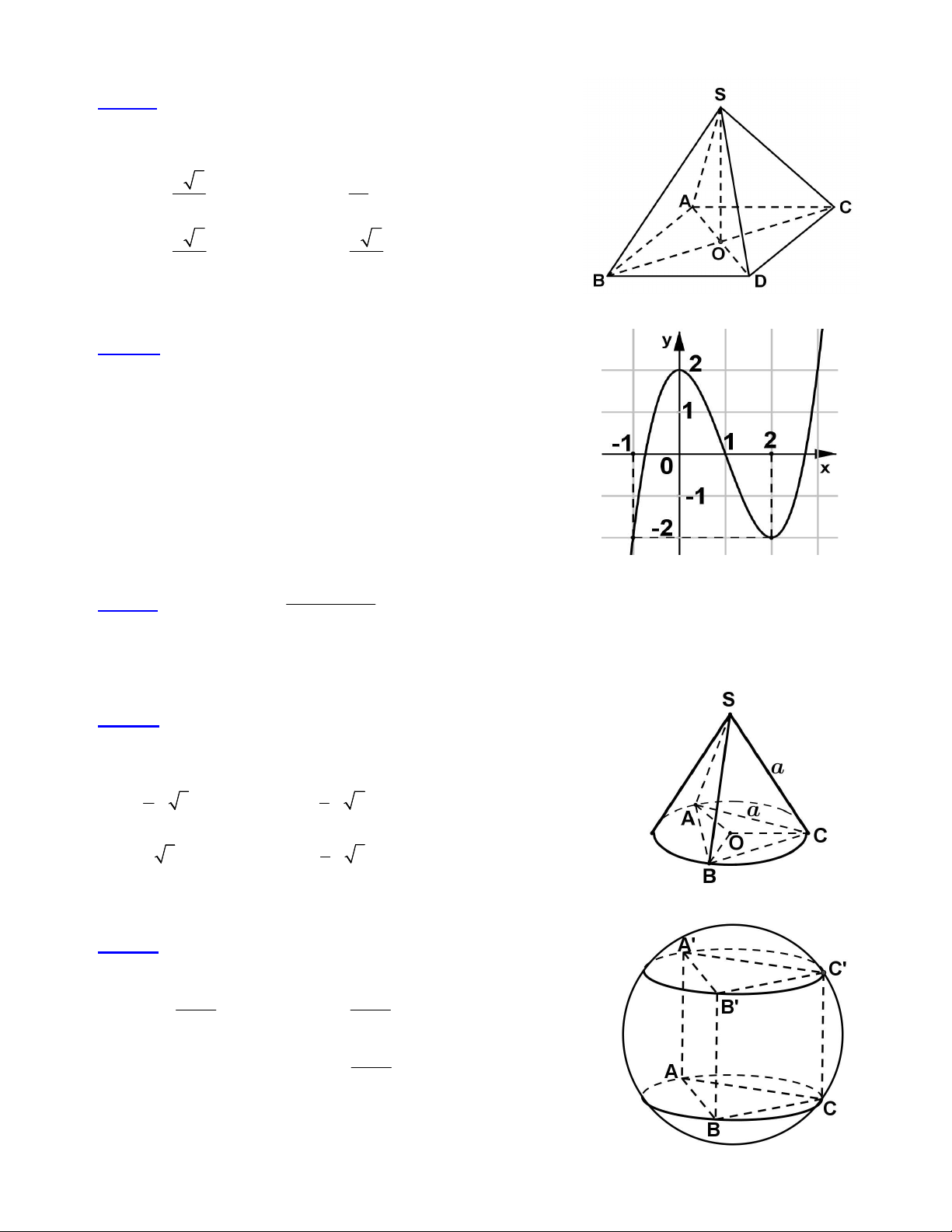
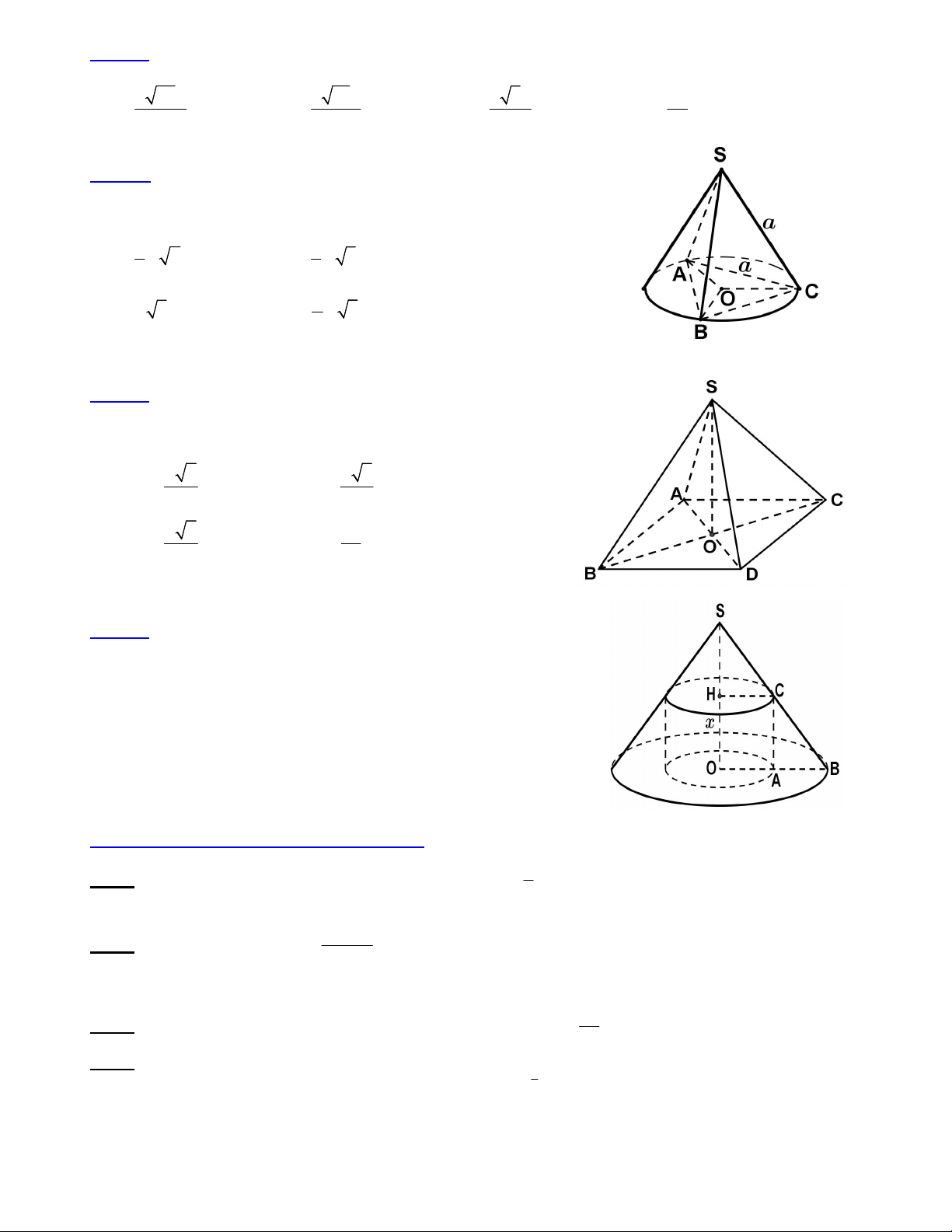
Câu 21: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA = a 3 và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là : a a 2 a 3 a 2 A. B. C. D. 2 6 2 4
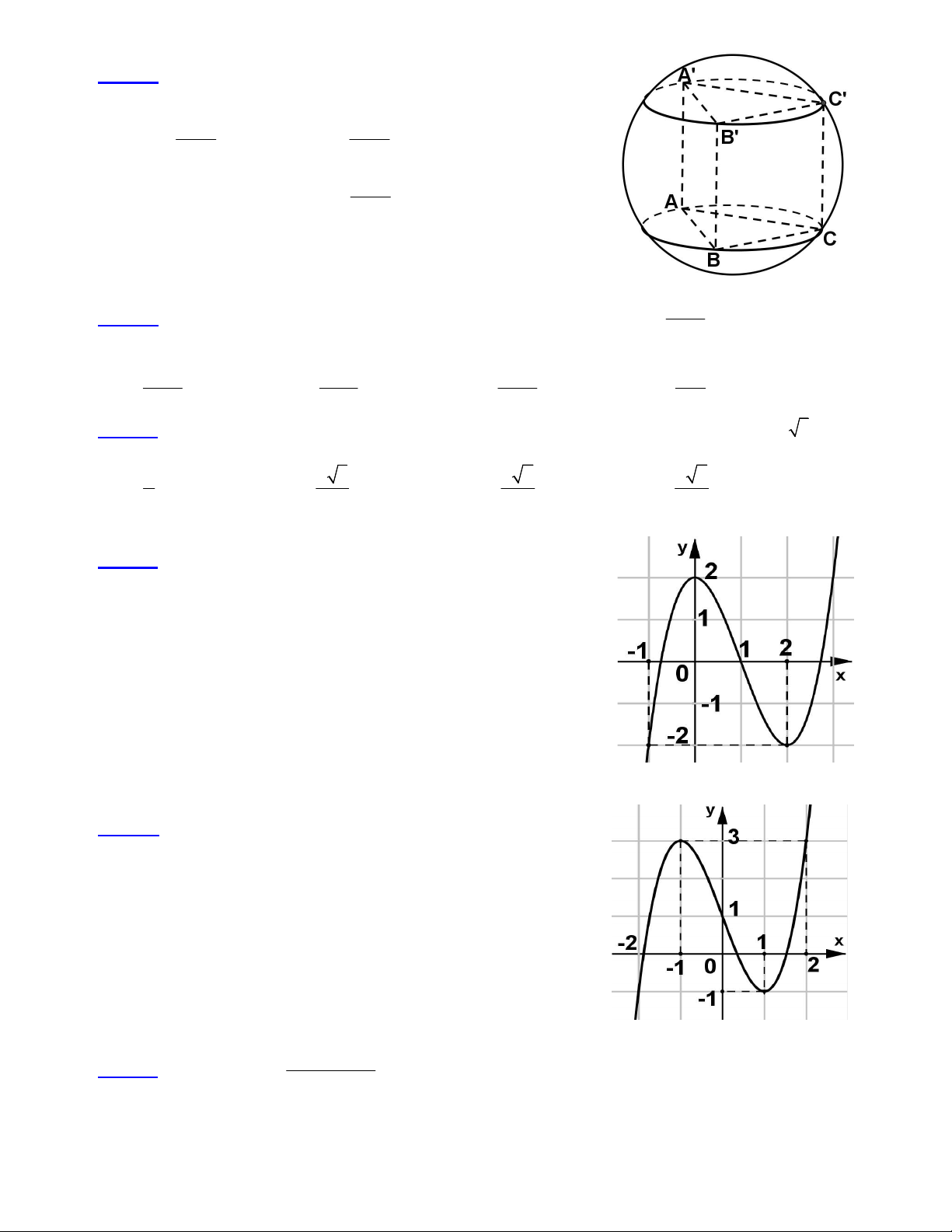
Câu 22: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là : 2 7 a 2 7 a A. S  B. S  2 3 2 7 a C. 2 S  7 a D. S  6
Câu 23: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là : 2 57 a 2 3a 2a 2 51a A. B. C. D. 19 7 3 17
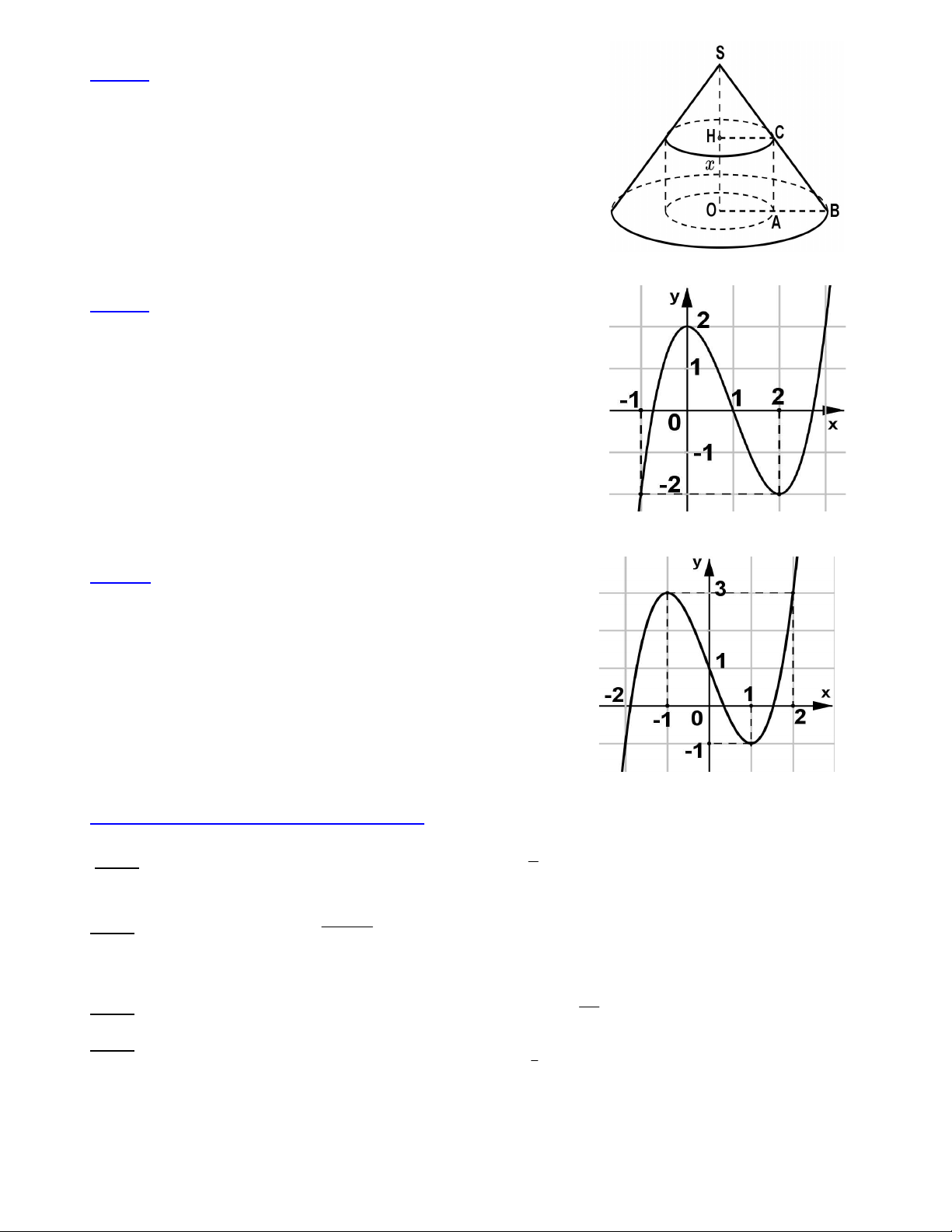
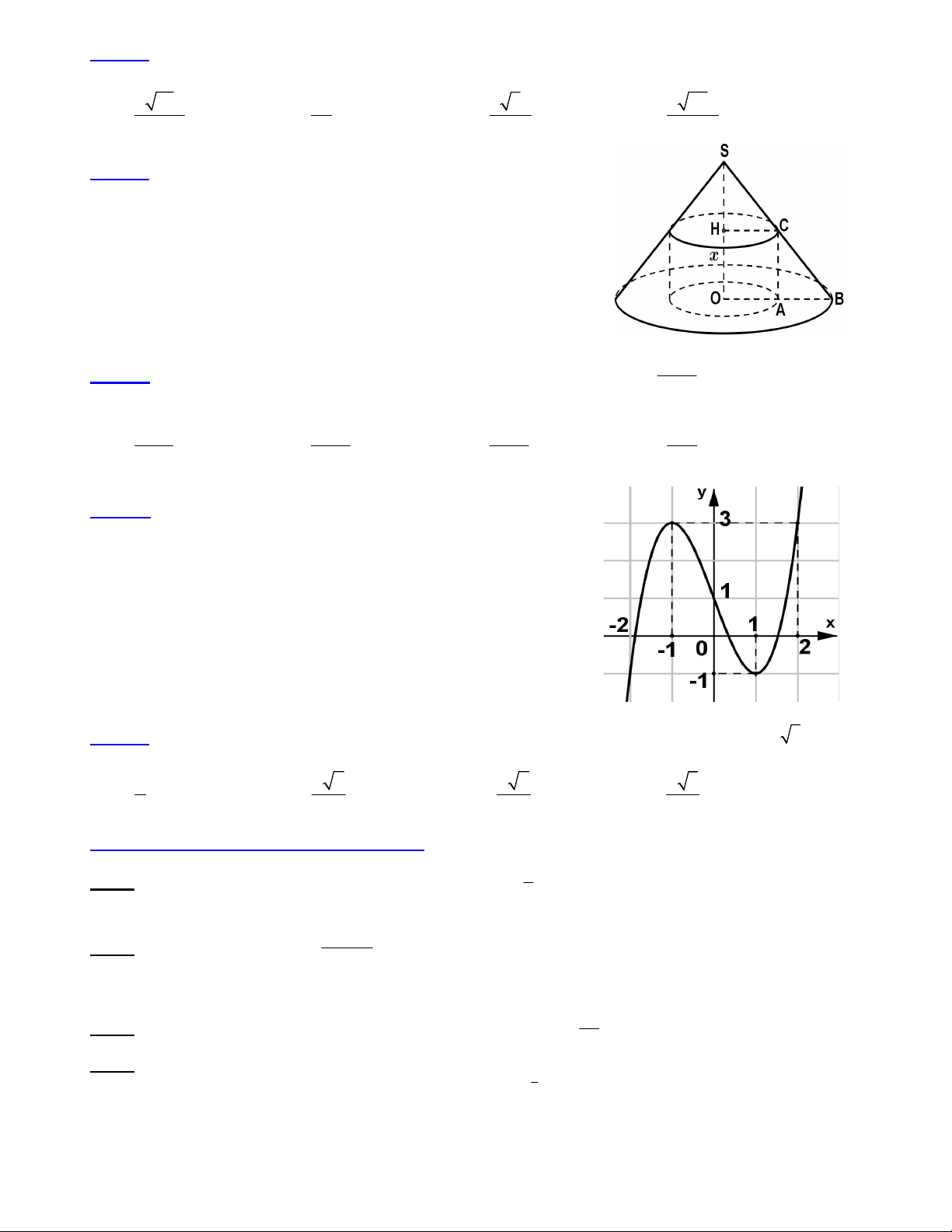
Câu 24: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất. A. x = 3m B. x = 4m C. x = 2m D. x = 1,5m
Câu 25: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 600. Bán kính R của mặt cầu
ngoại tiếp hình chóp S.ABCD đó là : a 5 a 6 A. R  B. R  3 2 3a a 6 C. R  D. R  2 3 2 5 a
Câu 26: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng . Khi đó thể tích của 3 hình nón bằng : 3 4 a 3 5 a 3 2 a 3  a A. B. C. D. 9 9 9 3 x 1 Câu 27: Cho hàm số y 
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị 2 x  2mx  9
của hàm số đã cho có đúng một đường tiệm cận đứng ? A. 4 B. 1 C. 2 D. 3
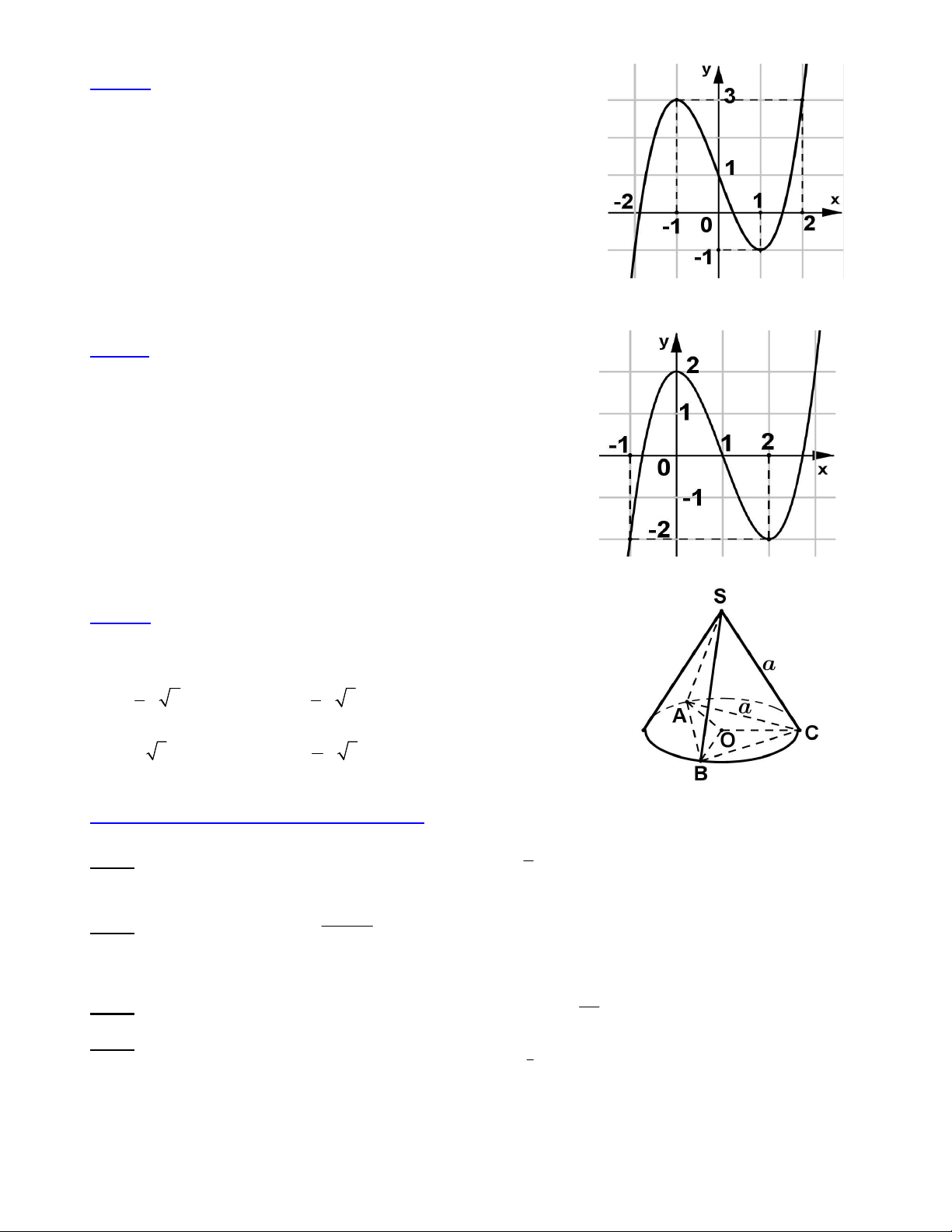
Câu 28: Cho hàm số y  f (x) có đồ thị như hình vẽ bên. Hàm số
y  f (1 cos x ) đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây : A. M + 2.m = 5 B. M + 2.m = 1 C. 2.M + m = 6 D. 2 2 M  m  9
Câu 29: Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình f  f (x)   2 có bao nhiêu nghiệm ? A. 4 B. 6 C. 5 D. 3
Câu 30: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là : 1 1 A. 2  2 a B. 2  3 a 3 3 1 C. 2  3 a D. 2  3 a 2
PHẦN II : TỰ LUẬN (4 điểm − 25 phút) -------------- 1
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số 3 2
y  x  mx  (m  6)x  2m 1 có cực đại và 3 cực tiểu. 2x  1
Bài 2: (1điềm) Cho hàm số y 
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có  x  2 hoành độ x  1. M 2 x
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên đoạn  1  ;1. x e
Bài 4: (1 điểm) Giải bất phương trình: log (x  4)  1  log x . 5 1 5
----------------------------------------------- ----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO KỲ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH
LỚP 12 − NĂM HỌC 2019 – 2020 TRƯỜNG THPT TRẦN PHÚ Môn thi : Toán
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(không kể thời gian phát đề) (Đề có 4 trang) Mã đề thi 151
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)  
Câu 1: Tập nghiệm S của bất phương trình: log  log x  0 là : 3 1    3  1 1 A. S  ( 0;1) B. S    ;   C. S   D. S    0;    3   3 
Câu 2: Tập xác định của hàm số y  ln(ln x ) là : A. 0;  B. (1:  ) C. ( 0;1) D. ( 0;   ) a 13
Câu 3: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD = . Gọi H là 2
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là : 3 a 3 2 a 3 2a A. B. C. D. 3 12a 3 3 3 2 x  2x  2  x  8
Câu 4: Giải bất phương trình: 2  3  2  3
ta được bao nhiêu nghiệm nguyên ? A. 4 B. 5 C. 6 D. Vô số
Câu 5: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm) A. 10 năm B. 9 năm C. 8 năm D. 11 năm
Câu 6: Một khối gỗ hình lập phương có thể tích bằng 1
V . Người thợ mộc gọt giũa khối gỗ đó thành một V
khối trụ có thể tích bằng 
. Giá trị lớn nhất của k là : 2 V . Đặt 2 k 1 V    1 A. kmax  B. k  C. k  D. k  3 max 2 max 4 max 4
Câu 7: Tìm m để hàm số 4 2
y  mx  2(m 1)x  2 (m là tham số) có hai cực tiểu và một cực đại. A. 0 < m < 1 B. m < 0 C. m > 2 D. 1 < m < 2 ax  b Câu 8: Cho hàm số y 
có đồ thị như hình vẽ bên. Tìm x 1
khẳng định đúng trong các khẳng định sau : A. b < 0 < a B. 0 < a < b C. 0 < b < a D. a < b < 0 x  2 Câu 9: Cho hàm số y 
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường x 1
thẳng (d) : y  3x  2 . A. 0 B. 3 C. 2 D. 1 2 ln x
Câu 10: Đạo hàm của hàm số y  bằng : x 2 2x ln x  ln x 2 2  ln x 2 2ln x  ln x 2 2ln x  ln x A. B. C. D. 2 x 2 x 2 x 2 x
Câu 11: Phương trình: 2x 1 3
 4.3x  1  0 có 2 nghiệm 1 x , 2 x trong đó  1 x 2
x . Khẳng định nào dưới đây là đúng ? A.   1 x . 2 x  1 B. 2 1 x   2 x 0 C. 1 x  2 2 x 1 D. 1 x    2 x 2
Câu 12: Trong các hàm số sau đây, hàm số nào nghịch biến trên R? A. 4 2 y   x  4x  5 B. 3 2 y  x  4x  cos x 4 C. 3 2
y   x  2x  x  5 D. 3 2
y   x  2x  7x 1 3 1 1 1 Câu 13: Hàm số 4 3 2
y  x  x  x  x  2 có bao nhiêu điểm cực trị ? 4 3 2 A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm 2 9  x
Câu 14: Đồ thị hàm số y 
có bao nhiêu đường tiệm cận ? 2 x  3x  4 A. 2 B. 1 C. 4 D. 3
Câu 15: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  x  3x  9x  1 trên đoạn 4;0. Tính M + m. A. M + m = 22 B. M + m = 24 C. M + m = 21 D. M + m = 29
Câu 16: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 600. Thể tích của khối lăng trụ ABC.A’B’C’ bằng : 3 3a 3 3a 3 2 a A. B. 3 3a C. D. 2 3 2 2 x  2  1 x 
Câu 17: Cho hàm số y   
. Tìm mệnh đề đúng trong các mệnh đề sau sau :  3 
A. Hàm số nghịch biến trên khoảng (1;   )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng (1;   )
D. Hàm số đồng biến trên R.
Câu 18: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ? A. Hàm số x 2019 y e   đồng biến trên R. B. log e  log e  2 a . b a C. log(ab) = loga + logb D. ln  0 b
Câu 19: Gọi x , x là nghiệm của phương trình: 2
log x  log 64. log x  4  0 . Tính giá trị của biểu thức 1 2 4 A  log  . 1 x log 2 x A. A  3 B. A  3 C. A   2 D. A  4 x x e  e
Câu 20: Đạo hàm của hàm số y  bằng : x x e  e 5 4 2x 2 2( x e  e ) A. B. C. x x e e  D. x x 2 x x 2 x x 2 (e e  ) (e  e ) (e  e ) x 1 Câu 21: Cho hàm số y 
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị 2 x  2mx  9
của hàm số đã cho có đúng một đường tiệm cận đứng ? A. 2 B. 3 C. 1 D. 4
Câu 22: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là : 2 7 a 2 7 a A. S  B. S  2 6 2 7 a C. 2 S  7 a D. S  3
Câu 23: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 600. Bán kính R của mặt cầu
ngoại tiếp hình chóp S.ABCD đó là : a 6 a 6 A. R  B. R  2 3 3a a 5 C. R  D. R  2 3 2 5 a
Câu 24: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng . Khi đó thể tích của 3 hình nón bằng : 3 4 a 3 5 a 3 2 a 3  a A. B. C. D. 9 9 9 3
Câu 25: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là : 1 A. 2  2 a B. 2  3 a 3 1 1 C. 2  3 a D. 2  3 a 2 3
Câu 26: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA = a 3 và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là : a a 2 a 3 a 2 A. B. C. D. 2 4 2 6
Câu 27: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là : 2 57 a 2a 2 3a 2 51a A. B. C. D. 19 3 7 17
Câu 28: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất. A. x = 3m B. x = 4m C. x = 2m D. x = 1,5m
Câu 29: Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình f  f (x)   2 có bao nhiêu nghiệm ? A. 3 B. 4 C. 5 D. 6
Câu 30: Cho hàm số y  f (x) có đồ thị như hình vẽ bên. Hàm số
y  f (1 cos x ) đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây : A. M + 2.m = 1 B. M + 2.m = 5 C. 2 2 M  m  9 D. 2.M + m = 6
PHẦN II : TỰ LUẬN (4 điểm − 25 phút) 1
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số 3 2
y  x  mx  (m  6)x  2m 1 có cực đại và 3 cực tiểu. 2x  1
Bài 2: (1điềm) Cho hàm số y 
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có  x  2 hoành độ x  1. M 2 x
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên đoạn  1  ;1. x e
Bài 4: (1 điểm) Giải bất phương trình : log (x  4)  1  log x . 5 1 5
----------------------------------------- ----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO KỲ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH
LỚP 12 − NĂM HỌC 2019 – 2020 TRƯỜNG THPT TRẦN PHÚ Môn thi : Toán
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(không kể thời gian phát đề) (Đề có 4 trang) Mã đề thi 152
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút)
Câu 1: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm) A. 10 năm B. 8 năm C. 9 năm D. 11 năm x  2 Câu 2: Cho hàm số y 
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường x 1
thẳng (d) : y  3x  2 . A. 1 B. 3 C. 2 D. 0 x x e  e
Câu 3: Đạo hàm của hàm số y  bằng : x x e  e 5 4 2x 2 2( x e  e ) A. B. C. x x e e  D. x x 2 x x 2 x x 2 (e e  ) (e  e ) (e  e )
Câu 4: Phương trình: 2x 1 3
 4.3x  1  0 có 2 nghiệm 1 x , 2 x trong đó 
. Khẳng định nào dưới đây 1 x 2 x là đúng ? A. 2 C.   1 x   B. 2 x 0 1 x . 2 x  1 1 x    D. 2 x 2 1 x  2 2 x 1
Câu 5: Trong các hàm số sau đây, hàm số nào nghịch biến trên R? A. 3 2 y  x  4x  cos x B. 3 2
y   x  2x  7x 1 4 C. 3 2
y   x  2x  x  5 D. 4 2 y   x  4x  5 3
Câu 6: Gọi x , x là nghiệm của phương trình: 2
log x  log 64. log x  4  0 . Tính giá trị của biểu thức 1 2 4 A  log  1 x log 2 x . A. A  3 B. A  3  C. A  2 D. A  4 ax  b Câu 7: Cho hàm số y 
có đồ thị như hình vẽ bên. Tìm x 1
khẳng định đúng trong các khẳng định sau : A. a < b < 0 B. 0 < a < b C. 0 < b < a D. b < 0 < a
Câu 8: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  x  3x  9x  1 trên đoạn 4;0. Tính M + m. A. M + m = 24 B. M + m = 22 C. M + m = 29 D. M + m = 21
Câu 9: Tập xác định của hàm số y  ln(ln x ) là : A. ( 0;1) B. ( 0;   ) C. 0;  D. (1:  )  
Câu 10: Tập nghiệm S của bất phương trình: log  log x  0 là : 3 1    3  1 1 A. S  ( 0;1) B. S    0;   C. S    ;   D. S    3   3  2 9  x
Câu 11: Đồ thị hàm số y 
có bao nhiêu đường tiệm cận ? 2 x  3x  4 A. 4 B. 1 C. 2 D. 3 1 1 1 Câu 12: Hàm số 4 3 2
y  x  x  x  x  2 có bao nhiêu điểm cực trị ? 4 3 2 A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm 2 x  2x  2  x  8
Câu 13: Giải bất phương trình: 2  3  2  3
ta được bao nhiêu nghiệm nguyên ? A. 5 B. Vô sô C. 6 D. 4
Câu 14: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ? A. Hàm số x 2019 y e   đồng biến trên R. B. log e  log e  2 a . b a C. log(ab) = loga + logb D. ln  0 b
Câu 15: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 600. Thể tích của khối lăng trụ ABC.A’B’C’ bằng : 3 3a 3 3a 3 2 a A. B. 3 3a C. D. 2 3 2 2 x  2  1 x 
Câu 16: Cho hàm số y   
. Tìm mệnh đề đúng trong các mệnh đề sau sau :  3 
A. Hàm số nghịch biến trên khoảng (1;   )
B. Hàm số nghịch biến trên R
C. Hàm số đồng biến trên khoảng (1;   )
D. Hàm số đồng biến trên R.
Câu 17: Một khối gỗ hình lập phương có thể tích bằng 1
V . Người thợ mộc gọt giũa khối gỗ đó thành một V
khối trụ có thể tích bằng  2 V . Đặt 2 k
. Giá trị lớn nhất của k là : 1 V   1  A. kmax  B. k  C. k  D. k  3 max 4 max 4 max 2 a 13
Câu 18: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD = . Gọi H là 2
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là : 3 a 3 2a 3 2 a A. B. 3 12a C. D. 3 3 3 2 ln x
Câu 19: Đạo hàm của hàm số y  bằng : x 2 2x ln x  ln x 2 2  ln x 2 2ln x  ln x 2 2ln x  ln x A. B. C. D. 2 x 2 x 2 x 2 x
Câu 20: Tìm m để hàm số 4 2
y  mx  2(m 1)x  2 (m là tham số) có hai cực tiểu và một cực đại. A. 0 < m < 1 B. m < 0 C. m > 2 D. 1 < m < 2
Câu 21: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 600. Bán kính R của mặt cầu
ngoại tiếp hình chóp S.ABCD đó là : a 5 3a A. R  B. R  3 2 a 6 a 6 C. R  D. R  3 2
Câu 22: Cho hàm số y  f (x) liên tục trên R và có đồ thị như
hình vẽ bên. Hỏi phương trình f  f (x)   2 có bao nhiêu nghiệm ? A. 5 B. 3 C. 4 D. 6 x 1 Câu 23: Cho hàm số y 
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị 2 x  2mx  9
của hàm số đã cho có đúng một đường tiệm cận đứng ? A. 3 B. 2 C. 4 D. 1
Câu 24: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là : 1 1 A. 2  3 a B. 2  2 a 2 3 1 C. 2  3 a D. 2  3 a 3
Câu 25: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là : 2 7 a 2 7 a A. S  B. S  2 3 2 7 a C. 2 S  7 a D. S  6
Câu 26: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là : 2 51a 2a 2 3a 2 57 a A. B. C. D. 17 3 7 19
Câu 27: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất. A. x = 3m B. x = 4m C. x = 2m D. x = 1,5m 2 5 a
Câu 28: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng . Khi đó thể tích của 3 hình nón bằng : 3 5 a 3 4 a 3 2 a 3  a A. B. C. D. 9 9 9 3
Câu 29: Cho hàm số y  f (x) có đồ thị như hình vẽ bên. Hàm số
y  f (1 cos x ) đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây : A. M + 2.m = 5 B. M + 2.m = 1 C. 2.M + m = 6 D. 2 2 M  m  9
Câu 30: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a .Cạnh SA = a 3 và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là : a a 2 a 2 a 3 A. B. C. D. 2 4 6 2
PHẦN II : TỰ LUẬN (4 điểm − 25 phút) 1
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số 3 2
y  x  mx  (m  6)x  2m 1 có cực đại và 3 cực tiểu. 2x  1
Bài 2: (1điềm) Cho hàm số y 
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có  x  2 hoành độ x  1. M 2 x
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên đoạn  1  ;1. x e
Bài 4: (1 điểm) Giải bất phương trình : log (x  4)  1  log x . 5 1 5 ---------------------- ----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO KỲ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH
LỚP 12 − NĂM HỌC 2019 – 2020 TRƯỜNG THPT TRẦN PHÚ Môn thi : Toán
Thời gian làm bài: 90 phút; ĐỀ CHÍNH THỨC
(không kể thời gian phát đề) (Đề có 4 trang) Mã đề thi 154
PHẦN I : TRẮC NGHIỆM (6 điểm − 65 phút) a 13
Câu 1: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , cạnh SD = . Gọi H là 2
trung điểm của AB ; SH vuông góc với mp(ABCD). Thể tích khối chóp S.ABCD là : 3 a 3 2a 3 2 a A. B. 3 12a C. D. 3 3 3
Câu 2: Phương trình: 2x 1 3
 4.3x  1  0 có 2 nghiệm 1 x , 2 x trong đó 
. Khẳng định nào dưới đây 1 x 2 x là đúng ? A. 2 C.   D. 1 x   B. 2 x 0 1 x . 2 x  1 1 x  2 2 x 1 1 x    2 x 2
Câu 3: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông cân tại B, AB = a. Mặt phẳng
(A’BC) hợp với mặt đáy (ABC) một góc bằng 600. Thể tích của khối lăng trụ ABC.A’B’C’ bằng : 3 3a 3 3a 3 2a A. B. 3 3a C. D. 2 3 2
Câu 4: Một khối gỗ hình lập phương có thể tích bằng 1
V . Người thợ mộc gọt giũa khối gỗ đó thành một V
khối trụ có thể tích bằng 
. Giá trị lớn nhất của k là : 2 V . Đặt 2 k 1 V   1  A. kmax  B. k  C. k  D. k  3 max 4 max 4 max 2 2 x  2  1 x 
Câu 5: Cho hàm số y   
. Tìm mệnh đề đúng trong các mệnh đề sau sau :  3 
A. Hàm số nghịch biến trên khoảng (1;   )
B. Hàm số đồng biến trên R.
C. Hàm số nghịch biến trên R
D. Hàm số đồng biến trên khoảng (1;   ) 2 ln x
Câu 6: Đạo hàm của hàm số y  bằng : x 2 2x ln x  ln x 2 2  ln x 2 2ln x  ln x 2 2ln x  ln x A. B. C. D. 2 x 2 x 2 x 2 x
Câu 7: Trong các hàm số sau đây, hàm số nào nghịch biến trên R? A. 4 2 y   x  4x  5 B. 3 2
y   x  2x  7x 1 4 C. 3 2 y  x  4x  cos x D. 3 2
y   x  2x  x  5 3
Câu 8: Gọi M, m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3 2
y  x  3x  9x  1 trên đoạn 4;0. Tính M + m. A. M + m = 21 B. M + m = 29 C. M + m = 24 D. M + m = 22 1 1 1 Câu 9: Hàm số 4 3 2
y  x  x  x  x  2 có bao nhiêu điểm cực trị ? 4 3 2 A. 1 điểm B. 3 điểm C. 2 điểm D. 4 điểm x  2 Câu 10: Cho hàm số y 
có đồ thị (C). Hỏi đồ thị (C) có bao nhiêu tiếp tuyến song song với đường x 1
thẳng (d) : y  3x  2 . A. 2 B. 3 C. 0 D. 1 x x e  e
Câu 11: Đạo hàm của hàm số y  bằng : x x e  e 5 2x 2 2(  x e  e ) 4 A. B. C. D. x x e e  x x 2 x x 2 x x 2 (e  e ) (e e  ) (e  e )
Câu 12: Cho hai số thực a và b thỏa mãn: e < a < b. Mệnh đề nào dưới đây là sai ? A. Hàm số x 2019 y e   đồng biến trên R. B. log(ab) = loga + logb a C. ln  0 D. log e  log e  2 . b a b 2 9  x
Câu 13: Đồ thị hàm số y 
có bao nhiêu đường tiệm cận ? 2 x  3x  4 A. 3 B. 4 C. 1 D. 2
Câu 14: Gọi x , x là nghiệm của phương trình: 2
log x  log 64. log x  4  0 . Tính giá trị của biểu thức 1 2 4 A  log  . 1 x log 2 x A. A  4 B. A  3 C. A  3  D. A  2 2 x  2x  2  x  8
Câu 15: Giải bất phương trình: 2  3  2  3
ta được bao nhiêu nghiệm nguyên ? A. 5 B. 6 C. 4 D. Vô sô
Câu 16: Tập xác định của hàm số y  ln(ln x ) là : A. 0;  B. (1:  ) C. ( 0;1) D. ( 0;   ) ax  b Câu 17: Cho hàm số y 
có đồ thị như hình vẽ bên. Tìm x 1
khẳng định đúng trong các khẳng định sau : A. 0 < a < b B. b < 0 < a C. a < b < 0 D. 0 < b < a
Câu 18: Một người gửi tiền vào ngân hàng với lãi suất 8,4% /năm và tiền lãi hàng năm được nhập vào tiền
vốn. Tính số năm tối thiểu người đó cần gửi để số tiền thu được nhiều hơn 2 lần số tiền gửi ban đầu. (lãi
suất không thay đổi trong thời gian gửi tiết kiệm) A. 8 năm B. 9 năm C. 10 năm D. 11 năm  
Câu 19: Tập nghiệm S của bất phương trình: log    là : 3 log1 x 0    3  1 1 A. S    0;   B. S   C. S    ;   D. S  ( 0;1)  3   3 
Câu 20: Tìm m để hàm số 4 2
y  mx  2(m 1)x  2 (m là tham số) có hai cực tiểu và một cực đại. A. 0 < m < 1 B. m < 0 C. 1 < m < 2 D. m > 2
Câu 21: Cho hình lăng trụ tam giác đều ABC.A’B’C’ có 9 cạnh
đều bằng a. Diện tích S của mặt cầu ngoại tiếp hình lăng trụ đó là : 2 7 a 2 7 a A. S  B. S  2 3 2 7 a C. 2 S  7 a D. S  6 2 5 a
Câu 22: Một hình nón có bán kính đáy bằng a và diện tích xung quanh bằng . Khi đó thể tích của 3 hình nón bằng : 3 4 a 3 5 a 3 2 a 3  a A. B. C. D. 9 9 9 3
Câu 23: Cho hỉnh chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh bằng a. Cạnh SA = a 3 và SA
vuông góc với mp(ABCD). Gọi G là trọng tâm tam giác SAB. Khoảng cách từ G đến mp(SAC) là : a a 3 a 2 a 2 A. B. C. D. 2 2 4 6
Câu 24: Cho hàm số y  f (x) liên tục trên R và có đồ thị như hình vẽ
bên. Hỏi phương trình f  f (x)   2 có bao nhiêu nghiệm ? A. 6 B. 3 C. 5 D. 4
Câu 25: Cho hàm số y  f (x) có đồ thị như hình vẽ bên. Hàm số
y  f (1 cos x ) đạt giá trị lớn nhất và giá trị nhỏ nhất lần lượt là M
và m. Tìm khẳng định đúng trong các khẳng định dưới đây : A. 2 2 M  m  9 B. M + 2.m = 1 C. 2.M + m = 6 D. M + 2.m = 5 x 1 Câu 26: Cho hàm số y 
(m là tham số, m ≠ 0). Hỏi có bao nhiêu giá tri thực của m để đồ thị 2 x  2mx  9
của hàm số đã cho có đúng một đường tiệm cận đứng ? A. 4 B. 1 C. 2 D. 3
Câu 27: Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác đều cạnh bằng a, cạnh bên AA’ = 2a. Gọi
M là trung điểm của B’C’. Khoảng cách từ M đến mp(A’BC) là : 2 57 a 2 51a 2 3a 2a A. B. C. D. 19 17 7 3
Câu 28: Một hình tứ diện đều có cạnh bằng a , có một đỉnh trùng với
đỉnh của hình nón, ba đỉnh còn lại nằm trên đường tròn đáy của hình nón.
Khi đó diện tích xung quanh của hình nón là : 1 1 A. 2  2 a B. 2  3 a 3 3 1 C. 2  3 a D. 2  3 a 2
Câu 29: Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a ,
góc giữa cạnh bên và mặt đáy bằng 600. Bán kính R của mặt cầu
ngoại tiếp hình chóp S.ABCD đó là : a 6 a 5 A. R  B. R  3 3 a 6 3a C. R  D. R  2 2
Câu 30: Một nóc nhà cao tầng có dạng một hình nón. Người ta muốn
xây một cái bể có dạng hình trụ nội tiếp trong hình nón để chứa nước
(như hình vẽ minh họa). Cho biết SO = 6m ; OB = 5m và OH = x (m),
(0 < x < 6). Tìm x để cái bể hình trụ có thể tích lớn nhất. A. x = 3m B. x = 4m C. x = 2m D. x = 1,5m
PHẦN II : TỰ LUẬN (4 điểm − 25 phút) 1
Bài 1: (1 điêm) Tìm các giá trị của tham số m để hàm số 3 2
y  x  mx  (m  6)x  2m 1 có cực đại và 3 cực tiểu. 2x  1
Bài 2: (1điềm) Cho hàm số y 
có đồ thị (C). Viết phương trình tiếp tuyến tại điểm M thuộc (C) có  x  2 hoành độ x  1. M 2 x
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y  trên đoạn  1  ;1. x e
Bài 4: (1 điểm) Giải bất phương trình : log (x  4)  1  log x . 5 1 5
----------------------------------------------- ----------- HẾT ----------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm. KIỂM TRA HỌC KỲ I TOÁN 12 NH 2019 − 2020 ĐÁP ÁN PHẦN TỰ LUẬN
Bài 1: (1 điêm) Tìm các giá trị của tham số m để
Bài 3: (1 điểm) Tìm giá trị lớn nhất, giá trị nhỏ 1 2 hàm số 3 2
y  x  mx  (m  6)x  2m 1 có cực x   3 nhất của hàm số y trên đoạn  1;1. x e đại và cực tiểu. 2 2x  x 2
y '  x  2mx  m  6 0,25đ y '  0,25đ x e Để hàm số có CĐ, CT x  n y’ 0  2 0 ( ) 2x  x  0   0,25đ
 PT y’  0 có 2 nghiệm phân biệt x  2 (loai) a  0   0,25đ Ta có : f ( 1  )  e  '  0 f (0)  0 1  2 m  m  6  0 0,25đ f (1)  e m  2
Vậy : min y  0 ; max y  e 0,5đ  1;   0,25đ 1 1; 1 m  3 2x  1
Bài 4: (1 điểm) Giải bất phương trình:
Bài 2: (1điềm) Cho hàm số y  có đồ thị  x  2
log (x  4)  1  log x . 5 1
(C). Viết phương trình tiếp tuyến tại điểm M thuộc 5 (C) có hoành độ x  1. M ĐK : x > 0 0,25đ 5 y '  0,25đ 2 (x  2) x  4 1 BPT   0,25đ 5 x  y’(1)  5 0,25đ 2  x  4x  5  0 x  1  y  3 0,25đ M M   5  x  1 0,25đ PTTT : y  5x − 2 0,25đ
So với đk trên, nghiệm BPT là : 0 < x  1 0,25đ TRƯỜNG THPT TRẦN PHÚ
KIỂM TRA HỌC KỲ 1 NĂM HỌC 2019 - 2020
ĐÁP ÁN TRẮC NGHIỆM TOÁN KHỐI 12 (CHỈNH SỬA) Mã đề Mã đề Câu Câu Câu Câu Mã đề 151 Mã đề 152 153 154 1 D 1 C 1 A 1 D 2 B 2 A 2 C 2 C 3 B 3 B 3 B 3 A 4 C 4 D 4 B 4 B 5 B 5 C 5 C 5 A 6 C 6 B 6 C 6 D 7 A 7 C 7 C 7 D 8 C 8 C 8 D 8 B 9 D 9 D 9 C 9 A 10 D 10 B 10 A 10 D 11 C 11 B 11 A 11 C 12 C 12 A 12 D 12 C 13 A 13 C 13 D 13 C 14 B 14 D 14 B 14 C 15 D 15 A 15 A 15 B 16 A 16 A 16 B 16 B 17 A 17 B 17 D 17 D 18 D 18 D 18 D 18 B 19 A 19 D 19 B 19 A 20 B 20 A 20 A 20 A 21 B 21 C 21 B 21 B 22 D 22 A 22 B 22 A 23 B 23 A 23 A 23 D 24 A 24 D 24 C 24 C 25 D 25 B 25 D 25 B 26 D 26 D 26 A 26 D 27 A 27 C 27 D 27 A 28 C 28 B 28 B 28 B 29 C 29 B 29 C 29 A 30 A 30 C 30 B 30 C