Đề thi HK1 Toán 12 năm học 2017 – 2018 sở GD và ĐT Hà Nam

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2017 – 2018 .Mời bạn đọc đón xem.

19 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

7 trang 8 tháng trước

Tác giả:

Profile Lan Tường
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HÀ NAM
(Đề thi gồm 02 trang)
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ I
Năm học 2017 – 2018
Môn: Toán
Thời gian làm bài: 90 phút
I. PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1: Tìm số giao điểm của đồ thị hàm số
3
232yx x và Parabol
2
10 4.yx x
A. 0. B. 1. C. 3. D. 2.
Câu 2: Cho hàm số

log 2 4 .gx x
Tính

1.g
A.

1
1.
2ln10
g

B.

1
1.
ln10
g

C.

1
1.
2ln10
g

D.

1
1.
ln10
g

Câu 3:
Cho hình nón tròn xoay có diện tích xung quanh bằng
16
và độ dài đường sinh bằng
8.
Tính bán kính đường tròn đáy r của hình nón đã cho.
A. 4.r B.
1
.
2
r C. 2.r D. 1.r
Câu 4: Hàm số
42
11
42
yxx có bao nhiêu điểm cực trị ?
A. 1. B. 2. C. 3. D. 0.
Câu 5: Cho hàm số .sin .
x
y
ex
Khẳng định nào sau đây là đúng ?
A.

2
22
.
2
x
y
y
e


B.

2
2
.
2
x
y
y
e


C.

2
2
.
4
x
y
y
e


D.

2
22
.
4
x
y
y
e


Câu 6: Tìm số đường tiệm cận của đồ thị hàm số
2
2
21
.
252
x
y
xx

A. 4. B. 3. C. 2. D. 1.
Câu 7: Cho khối chóp .S ABC có ,,SA SB SC đôi một vuông góc; ,,2.
2
a
SA a SB SC a
Tính thể tích
V của khối chóp ..S ABC
A.
3
1
.
2
Va
B.
3
1
.
3
Va
C.
3
.Va D.
3
1
.
6
Va
Câu 8: Biết
23
log 3 , log 5 .ab Tính
1000
log 27 theo ,.ab
A.
.
1
b
ab
B.
.
1
a
ab
C.
.
1
ab
ab
D.
1
.
1 ab
Câu 9: Biết hàm số
32
534yx x x  nghịch biến trên khoảng

;ab
với ; ,abab
và đồng biến trên các khoảng

;,; .ab  Tính 33.Sab
A. 6.S B. 9.S C. 10.S D. 12.S
Câu 10: Cho tứ diện .S ABC có đáy ABC là tam giác đều cạnh .a Biết SA vuông góc với
mặt phẳng

ABC và
.SA a
Tính bán kính của mặt cầu ngoại tiếp tứ diện
.S ABC
theo
.a
Mã đề 124
A.
7
.
4
a
R
B.
7
.
12
Ra
C.
7
.
3
a
R
D.
7
.
12
a
R
Câu 11: Gọi
12
,
x
x là các nghiệm của phương trình
2
1
1
927.
x
x
x
x
Tính
12
.Txx
A. 2.T B. 2.T  C. 6.T D. 6.T 
Câu 12: Tìm tập xác định D của hàm số

2
ln 5 4 .yxx
A.

1; 4 .D B.

4; .D 
C.

;1 .D 
D.

;1 4; .D 
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1 (1,5 điểm). Cho hàm số
32
452.yx x x
a)
Khảo sát sự biến thiên và vẽ đồ thị

C của hàm số.
b) Gọi ,AB là các điểm cực trị của

.C Cho
11
;1.
2
C



Chứng minh rằng các điểm
,A ,
C thẳng hàng.
Bài 2 (1,5 điểm). Giải các phương trình sau:
a)
1
1
94.3 0.
3
xx

b)


42
42
log 6 9 log 5 .
x
xx
Bài 3 (3,0 điểm). Cho hình chóp .SABCD có đáy ABCD là hình chữ nhật và 2,
A
Da
2.CD a
Biết
SA
vuông góc với mặt phẳng

ABCD và
32.SA a
Gọi K là trung điểm
của đoạn
.
A
D
a)
Tính thể tích khối chóp .SBCK theo .a
b)
Tính khoảng cách giữa hai đường thẳng ,SB AD theo
.a
c)
Chứng minh rằng

SBK
vuông góc với

.SAC
Bài 4 (1,0 điểm). Cho , ,abc là các số thực dương. Tìm giá trị lớn nhất của biểu thức

222
49
.
22
4
P
ab a cb c
abc



---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT MÃ ĐỀ 124
THỰC HIỆN BỞI NGUYỄN THẾ DUY
https://www.facebook.com/theduy1995
I. PHẦN TRẮC NGHIỆM
1. C 2. D 3. C 4. A 5. D 6. B
7. D 8. B 9. C 10. B 11. A 12. A
Câu 1: Tìm số giao điểm của đồ thị hàm số
3
232yx x và Parabol
2
10 4.yx x
A. 0. B. 1. C. 3. D. 2.
HD: Phương trình hoành độ giao điểm của

C và

P là
32
232 104
x
xxx

32
2; 3
2136021230 .
1
2
xx
xx x x x x
x


Vậy hai đồ thị hàm số cắt nhau tại 3 điểm phân biệt.
Chọn C.
Câu 2: Cho hàm số

log 2 4 .gx x Tính

1.g
A.

1
1.
2ln10
g

B.

1
1.
ln10
g

C.

1
1.
2ln10
g

D.

1
1.
ln10
g

HD:
Ta có
 


11
log 2 log 2 1 .
2 .ln10 ln10
gx x g x g
x


Chọn D.
Câu 3: Cho hình nón tròn xoay có diện tích xung quanh bằng 16
và độ dài đường sinh bằng
8. Tính bán kính đường tròn đáy r của hình nón đã cho.
A.
4.r
B.
1
.
2
r C.
2.r
D.
1.r
HD: Ta có
16
16
16
2.
8
8
8
xq
S
rl
r
l
l



Chọn C.
Câu 4: Hàm số
42
11
42
yxx có bao nhiêu điểm cực trị ?
A. 1. B. 2. C. 3. D. 0.
HD: Hàm số trùng phương

42
0yax bx ca với tích 0ab có 1 điểm cực trị.
Vậy hàm số
42
11
42
yxx
có duy nhất 1 điểm cực trị là
0.x Chọn A.
Câu 5: Cho hàm số .sin .
x
y
ex
Khẳng định nào sau đây là đúng ?
A.

2
22
.
2
x
y
y
e


B.

2
2
.
2
x
y
y
e


C.

2
2
.
4
x
y
y
e


D.

2
22
.
4
x
y
y
e


HD: Ta có

.sin .cos cos sin
x
xx
y
exe x xxe



sin cos cos sin 2 .cos
xxx
y
xxe xxe e x



.cos .
2
x
y
ex


Khi đó

2
22
22222
.sin .cos sin cos .
2
x
xxx
y
y
ex e x x xee






Chọn D.
Câu 6: Tìm số đường tiệm cận của đồ thị hàm số
2
2
21
.
252
x
y
xx

A.
4.
B.
3.
C.
2.
D.
1.
HD:
Hàm số đã cho dạng phân thức


ux
y
vx
và có đồ thị

C ta thấy rằng:
 
deg degux vx
(với deg là bậc của đa thức)

C
có tiệm cận ngang là 0.y
Phương trình

0vx
1
2
2
x
x

C có hai tiệm cận đứng là
1
.
2
2
x
x
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận.
Chọn B.
Câu 7: Cho khối chóp .S ABC có , ,SA SB SC đôi một vuông góc;
,,2.
2
a
SA a SB SC a

Tính thể tích V của khối chóp ..S ABC
A.
3
1
.
2
Va
B.
3
1
.
3
Va
C.
3
.Va
D.
3
1
.
6
Va
HD: Khối chóp .S ABC có ,,SA SB SC đôi một vuông góc
.
..
.
6
S ABC
SA SB SC
V

Với
,,2
2
a
SA a SB SC a

Thể tích
3
.
..2
2
.
66
S ABC
a
aa
a
V
 Chọn D.
Câu 8: Biết
23
log 3 , log 5 .ab Tính
1000
log 27 theo , .ab
A. .
1
b
ab
B. .
1
a
ab
C. .
1
ab
ab
D.
1
.
1
ab
HD: Ta có

3
3
22
1000 10
10
22
log 27 log 311 1
log 27 log 27 log 27 . . .
33log103log2.5

22
223
3.log 3 3.log 311 13
.. . .
31 log 5 31 log 3.log5 31 1
aa
ab ab


Chọn B.
Câu 9: Biết hàm số
32
534yx x x  nghịch biến trên khoảng

;ab
với ; ,abab
và đồng biến trên các khoảng

;,; .ab  Tính 33.Sab
A.
6.S
B.
9.S
C.
10.S
D.
12.S
HD: Xét hàm số
32
534yx x x  trên , có
2
3103; .yx x x

Phương trình

2
1
03 1030 31 30 .
3
3
x
yxx xx
x
  
Suy ra hàm số đồng biến trên khoảng
1
;
3




và

3;  ; hàm số nghịch biến trên
1
;3 .
3



Do đó
1
;3
3
ab
1
3 3 3. 3.3 10.
3
Sab Chọn C.
Câu 10: Cho tứ diện .S ABC có đáy
A
BC là tam giác đều cạnh .a Biết SA vuông góc với
mặt phẳng

A
BC
và .SA a Tính bán kính của mặt cầu ngoại tiếp tứ diện .S ABC theo .a
A.
7
.
4
a
R
B.
7
.
12
Ra
C.
7
.
3
a
R
D.
7
.
12
a
R
HD: “ Tứ diện ABCD có một cạnh vuông góc với một mặt, chẳng hạn có đường thẳng
A
B
vuông góc với mặt phẳng

.
B
CD Gọi
h
là chiều cao của tứ diện ,ABCD r là bán kính
đường tròn ngoại tiếp
.
B
CD
Khi đó, ta có công thức tính nhanh bán kính mặt cầu ngoại tiếp
tứ diện
A
BCD
là
2
2
4
h
Rr
”
Áp dụng CTTN, ta có
2
22
2
37
.
43412
ABC
SA a a
RR a





Chọn B.
Câu 11: Gọi
12
,
x
x là các nghiệm của phương trình
2
1
1
927.
x
x
x
x
Tính
12
.Txx
A. 2.T B. 2.T  C. 6.T D. 6.T 
HD: Điều kiện:
0
.
1
x
x

Ta có

22
11
3.
2.
11
2132
927 3 3 .
1
xx
xx
xx
xx
xx
xx






1
22 2
2
37
21 13 22236 620 .
37
x
xx xx x xxxx
x



Vậy tích
12
2.Txx Chọn A.
Câu 12: Tìm tập xác định
D
của hàm số

2
ln 5 4 .yxx
A.

1; 4 .D B.

4; .D 
C.

;1 .D  D.

;1 4; .D 
HD: Hàm số đã cho xác định khi và chỉ khi
2
5401 4.xx x
Vậy tập xác định của hàm số là

1; 4 .D Chọn A.
II. PHẦN TỰ LUẬN
Bài 1 (1,5 điểm). Cho hàm số
32
452.yx x x
a) Khảo sát sự biến thiên và vẽ đồ thị

C
của hàm số.
b) Gọi ,
A
B là các điểm cực trị của

.C Cho
11
;1.
2
C



Chứng minh rằng các điểm
,
A
,
C thẳng hàng.
Lời giải. a) Học sinh tự làm.
b) Ta có
2
385; .yxx x
 Phương trình

110
0.
554
3327
xy
y
xy






Khi đó

54
1; 0 , ;
327
AB



24
;
327
AB





và
9
;1.
2
AC





Vậy
27
4
AC AB
 
suy ra ba điểm , ,ABC thẳng hàng.
Bài 2 (1,5 điểm). Giải các phương trình sau:
a)
1
1
94.3 0.
3
xx
 b)


42
42
log 6 9 log 5 .
x
xx
Lời giải. a) Ta có

2
1
1
9 4.3 0 3. 3 4.3 1 0 3 1 3.3 1 0
3
xx x x x x
 
0
1
310 3 3 0
.
1
3.3 1 0 3 3
xx
xx
x
x







Vậy phương trình có tập nghiệm là
0; 1 .S 
b) Điều kiện:
5.x Ta có




2
2
42 2
42 2
2
log 6 9 log 5 log 3 log 5
x
xxx x 


222
22
1
log 3 log 5 3 5 2 0
2
x
xxxxxx
x


(tmđk).
Vậy phương trình có tập nghiệm là
1; 2 .S 
Bài 3 (3,0 điểm). Cho hình chóp .SABCD có đáy ABCD là hình chữ nhật và 2,
A
Da
2.CD a
Biết
SA
vuông góc với mặt phẳng

ABCD và
32.SA a
Gọi K là trung điểm
của đoạn
.
A
D
a) Tính thể tích khối chóp .SBCK theo .a
b) Tính khoảng cách giữa hai đường thẳng ,SB AD theo .a
c) Chứng minh rằng

SBK
vuông góc với

.SAC
Lời giải. a) Ta có
2
2.
BKC ABCD ABK KCD
SSSSa


Suy ra thể tích khối chóp
.SBCK là
23
.
11
.. .3 2. 22
33
SBCK BCK
VSAS aaa
 (đvtt).
b) Vì
A
D // BC
A
D //
 

;;SBC d SB AD d A SBC
Kẻ AH vuông góc với
SB

HSB

A
HSBC
Tam giác
SAB vuông tại ,A có
22 2
111
A
HSAAB

K
C
A
D
B
S
H
Suy ra


22 2 2
.32.23
;.
5
32 2
SA AB a a a
dSBAD
SA AB
aa

c) Ta có

.. .2AC BK AB AD BA BD AB AD AB AD 
        


2
22
2
22
2. 222.20.AB AB AD AD AD AB a a
   
Suy ra
.0AC BK AC BK
 
mà SA BK

B
KSAC

.SBK SAC
Bài 4 (1,0 điểm). Cho , ,abc là các số thực dương. Tìm giá trị lớn nhất của biểu thức

222
49
.
22
4
P
ab a cb c
abc



Lời giải. Áp dụng bất đẳng thức AM – GM, ta có
 

22
222
4244
22 . 2 .
22
ab c a b ab ac bc
ab a cb c ab a b c


Đặt
222
4,t abc suy ra
2t
và

2
49
.
24
P
t
t

Xét hàm số


2
49
24
ft
t
t

với 2.t Ta có


2
2
2
49
04.
4
t
ft t
t
t

Tính các giá trị
 
2
5
4;lim
8
t
fft
 và

4
lim 0.
t
ft
Suy ra giá trị lớn nhất của hàm số

f
t là
5
.
8
Dấu
"" xảy ra 2.abc
Vậy giá trị nhỏ nhất của biểu thức
P là
5
.
8
| 1/7
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KÌ I HÀ NAM
Năm học 2017 – 2018
(Đề thi gồm 02 trang) Môn: Toán
Thời gian làm bài: 90 phút Mã đề 124 I.
PHẦN TRẮC NGHIỆM (3,0 điểm)
Câu 1: Tìm số giao điểm của đồ thị hàm số 3
y  2x  3x  2 và Parabol 2
y   x 10x  4. A. 0. B. 1. C. 3. D. 2.
Câu 2: Cho hàm số g x  log 2x  4. Tính g  1 .
A. g  1 1  .
B. g  1 1   . 2ln10 ln10
C. g  1 1   .
D. g  1 1  . 2ln10 ln10
Câu 3: Cho hình nón tròn xoay có diện tích xung quanh bằng 16 và độ dài đường sinh bằng
8. Tính bán kính đường tròn đáy r của hình nón đã cho. 1 A. r  4. B. r  . C. r  2.
D. r  1. 2 1 1 Câu 4: Hàm số 4 2
y x x  có bao nhiêu điểm cực trị ? 4 2 A. 1. B. 2. C. 3. D. 0. Câu 5: Cho hàm số  x y e .sin .
x Khẳng định nào sau đây là đúng ? y y y y 2  2 2  2 2  2 2  2 A. 2 x y   e . B. x y   e . C. x y   e . D. 2 x y   e . 2 2 4 4 2 2x 1
Câu 6: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 2x  5x  2 A. 4. B. 3. C. 2. D. 1. a
Câu 7: Cho khối chóp S.ABC có ,
SA SB, SC đôi một vuông góc; SA a, SB  , SC  2 . a 2
Tính thể tích V của khối chóp S.ABC. 1 1 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 2 3 6
Câu 8: Biết log 3  a, log 5  . b Tính log 27 theo a, . b 2 3 1000 b a ab 1 A. . B. . C. . D. . 1 ab 1 ab 1 ab 1 ab
Câu 9: Biết hàm số 3 2
y x  5x  3x  4 nghịch biến trên khoảng  ;
a b với a  ; b a, b  
và đồng biến trên các khoảng  ;  a,  ;
b  . Tính S  3a  3 . b A. S  6. B. S  9. C. S  10.
D. S  12.
Câu 10: Cho tứ diện S.ABC có đáy ABC là tam giác đều cạnh .
a Biết SA vuông góc với
mặt phẳng  ABC và SA  .
a Tính bán kính của mặt cầu ngoại tiếp tứ diện S.ABC theo . a a 7 7 a 7 a 7 A. R  .
B. R a . C. R  . D. R  . 4 12 3 12  x  2 x 1
Câu 11: Gọi x , x là các nghiệm của phương trình x 1 9 x  27
. Tính T x x . 1 2 1 2 A. T  2. B. T   2. C. T  6.
D. T   6.
Câu 12: Tìm tập xác định D của hàm số y   2
ln  x  5x  4.
A. D  1;4.
B. D  4; .
C. D    ;1 .
D. D    
;1  4; .
II. PHẦN TỰ LUẬN (7,0 điểm)
Bài 1 (1,5 điểm). Cho hàm số 3 2
y x  4x  5x  2.
a) Khảo sát sự biến thiên và vẽ đồ thị C của hàm số. 11  b) Gọi ,
A B là các điểm cực trị của C. Cho C ; 1 . 
 Chứng minh rằng các điểm  2  ,
A B, C thẳng hàng.
Bài 2 (1,5 điểm). Giải các phương trình sau: x x  1 a) 1 9  4.3   0. b) log  4 2
x  6x  9  log 5  x . 4  2   3
Bài 3 (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AD  2a,
CD a 2. Biết SA vuông góc với mặt phẳng  ABCD và SA  3a 2. Gọi K là trung điểm của đoạn A . D
a) Tính thể tích khối chóp S.BCK theo . a
b) Tính khoảng cách giữa hai đường thẳng SB, AD theo . a
c) Chứng minh rằng SBK  vuông góc với SAC.
Bài 4 (1,0 điểm). Cho a, b, c là các số thực dương. Tìm giá trị lớn nhất của biểu thức 4 9 P   . 2 2 2
a b c  4 a b a  2cb  2c
---------- HẾT ----------
HƯỚNG DẪN GIẢI CHI TIẾT MÃ ĐỀ 124
THỰC HIỆN BỞI NGUYỄN THẾ DUY
https://www.facebook.com/theduy1995 I. PHẦN TRẮC NGHIỆM 1. C 2. D 3. C 4. A 5. D 6. B 7. D 8. B 9. C 10. B 11. A 12. A
Câu 1: Tìm số giao điểm của đồ thị hàm số 3
y  2x  3x  2 và Parabol 2
y   x 10x  4. A. 0. B. 1. C. 3. D. 2.
HD: Phương trình hoành độ giao điểm của C và P là 3 2
2x  3x  2   x 10x  4
x  2; x  3 3 2 2x x 13x 6 0
2x 1x 2x 3 0             1 . x   2
Vậy hai đồ thị hàm số cắt nhau tại 3 điểm phân biệt. Chọn C.
Câu 2: Cho hàm số g x  log 2x  4. Tính g  1 .
A. g  1 1  .
B. g  1 1   . 2ln10 ln10
C. g  1 1   .
D. g  1 1  . 2ln10 ln10 1 1
HD: Ta có g x  log 2  log x  2  g x       Chọn D. x   g   1 . 2 .ln10 ln10
Câu 3: Cho hình nón tròn xoay có diện tích xung quanh bằng 16 và độ dài đường sinh bằng
8. Tính bán kính đường tròn đáy r của hình nón đã cho. 1 A. r  4. B. r  . C. r  2.
D. r  1. 2 S 16   rl   xq 16 16 HD: Ta có     r   2. Chọn C. l   8 l   8 8 1 1 Câu 4: Hàm số 4 2
y x x  có bao nhiêu điểm cực trị ? 4 2 A. 1. B. 2. C. 3. D. 0.
HD: Hàm số trùng phương 4 2
y ax bx c a  0 với tích ab  0 có 1 điểm cực trị. 1 1 Vậy hàm số 4 2
y x x  có duy nhất 1 điểm cực trị là x  0. Chọn A. 4 2 Câu 5: Cho hàm số  x y e .sin .
x Khẳng định nào sau đây là đúng ? y y y y 2  2 2  2 2  2 2  2 A. 2 x y   e . B. x y   e . C. x y   e . D. 2 x y   e . 2 2 4 4 HD: Ta có  x    .sin  x
.cos  cos  sin  x y e x e x x x e      y
sin  cos  x  cos  sin  x   2 x y x x e x x e e .cos x   x  e .cos . x 2 2  y 2 2  Khi đó 2 y      x e
x   xe x   2 2 x x 2x 2 .sin .cos sin cos x e
e . Chọn D.  2  2 2x 1
Câu 6: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 2x  5x  2 A. 4. B. 3. C. 2. D. 1. u x
HD: Hàm số đã cho dạng phân thức y
và có đồ thị C ta thấy rằng: v x
 deg u x  deg vx (với deg là bậc của đa thức)  C có tiệm cận ngang là y  0.  1  1 x x
 Phương trình vx  0  
2  C  có hai tiệm cận đứng là  2 .   x  2 x  2
Vậy đồ thị hàm số đã cho có 3 đường tiệm cận. Chọn B. a
Câu 7: Cho khối chóp S.ABC có ,
SA SB, SC đôi một vuông góc; SA a, SB  , SC  2 . a 2
Tính thể tích V của khối chóp S.ABC. 1 1 1 A. 3 V a . B. 3 V a . C. 3 V a . D. 3 V a . 2 3 6 . SA . SB SC
HD: Khối chóp S.ABC có ,
SA SB, SC đôi một vuông góc  V  . S.ABC 6 a a . a .2a 3 a
Với SA a, SB  , SC  2a   Thể tích 2 V   . Chọn D. 2 S.ABC 6 6
Câu 8: Biết log 3  a, log 5  . b Tính log 27 theo a, . b 2 3 1000 b a ab 1 A. . B. . C. . D. . 1 ab 1 ab 1 ab 1 ab 3 1 1 log 27 1 log 3 HD: Ta có 2 2 log 27  log 27  log 27  .  . . 3 1000 10 10 3 3 log 10 3 log 2.5 2 2   1 3.log 3 1 3.log 3 1 3a a 2 2  .  .  .  . Chọn B.
3 1 log 5 3 1 log 3.log 5 3 1 ab 1 ab 2 2 3
Câu 9: Biết hàm số 3 2
y x  5x  3x  4 nghịch biến trên khoảng  ;
a b với a  ; b a, b  
và đồng biến trên các khoảng  ;  a,  ;
b  . Tính S  3a  3 . b A. S  6. B. S  9. C. S  10.
D. S  12. HD: Xét hàm số 3 2
y x  5x  3x  4 trên , có 2
y  3x 10x  3; x   .   1 x  Phương trình 2
y  0  3x 10x  3  0  3x   1  x  3  0   3.  x  3  1   1 
Suy ra hàm số đồng biến trên khoảng ;  
 và 3;  ; hàm số nghịch biến trên ;3 .    3   3  1 1
Do đó a  ; b  3 
S  3a  3b  3.  3.3  10. Chọn C. 3 3
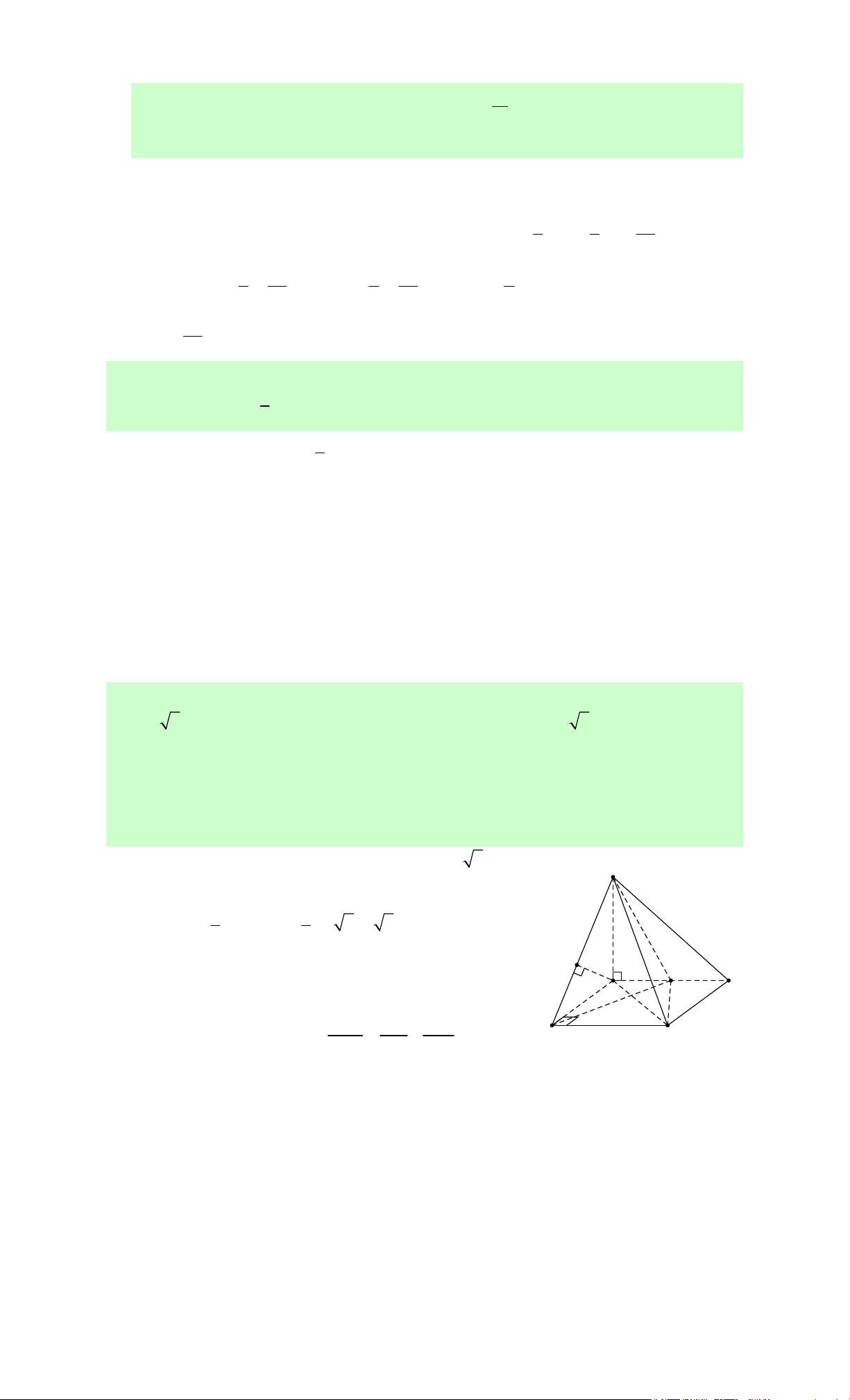
Câu 10: Cho tứ diện S.ABC có đáy ABC là tam giác đều cạnh .
a Biết SA vuông góc với
mặt phẳng  ABC và SA  .
a Tính bán kính của mặt cầu ngoại tiếp tứ diện S.ABC theo . a a 7 7 a 7 a 7 A. R  .
B. R a . C. R  . D. R  . 4 12 3 12
HD: “ Tứ diện ABCD có một cạnh vuông góc với một mặt, chẳng hạn có đường thẳng AB
vuông góc với mặt phẳng BCD. Gọi h là chiều cao của tứ diện ABCD, r là bán kính
đường tròn ngoại tiếp B .
CD Khi đó, ta có công thức tính nhanh bán kính mặt cầu ngoại tiếp 2 h tứ diện ABCD là 2 R r ” 4 2 2 2 SAa 3  a 7 Áp dụng CTTN, ta có 2 R R       a . Chọn B. ABC 4  3  4 12   x 1 x  2
Câu 11: Gọi x , x là các nghiệm của phương trình x 1 9 x  27
. Tính T x x . 1 2 1 2 A. T  2. B. T   2. C. T  6.
D. T   6. x  0  x  2  x  2 x 1 x 1 3. 2. 2 x 1 3 x  2 x 1 x 1     HD: Điều kiện:  . Ta có 9 x  27  3 x  3   . x  1 x x 1 x     2x   1  x  
1  3x x  2 3 7 2 2 2 1
 2x  2  3x  6x x  6x  2  0   . x  3  7  2
Vậy tích T x x  2. Chọn A. 1 2
Câu 12: Tìm tập xác định D của hàm số y   2
ln  x  5x  4.
A. D  1;4.
B. D  4; .
C. D    ;1 .
D. D    
;1  4; .
HD: Hàm số đã cho xác định khi và chỉ khi 2
x  5x  4  0  1  x  4.
Vậy tập xác định của hàm số là D  1;4. Chọn A. II. PHẦN TỰ LUẬN
Bài 1 (1,5 điểm). Cho hàm số 3 2
y x  4x  5x  2.
a) Khảo sát sự biến thiên và vẽ đồ thị C của hàm số. 11  b) Gọi ,
A B là các điểm cực trị của C. Cho C ; 1 . 
 Chứng minh rằng các điểm  2  ,
A B, C thẳng hàng.
Lời giải. a) Học sinh tự làm.
x  1  y   1  0  b) Ta có 2
y  3x  8x  5; x   .
 Phương trình y  0   5  5  4 . x   y      3  3  27        9  Khi đó A  5 4 1;0 , B ;     2 4 AB  ;    và AC  ; 1 .    3 27   3 27   2   27  Vậy AC AB suy ra ba điểm ,
A B, C thẳng hàng. 4
Bài 2 (1,5 điểm). Giải các phương trình sau: x x  1 a) 1 9  4.3   0. b) log  4 2
x  6x  9  log 5  x . 4  2   3 x x  1 2
Lời giải. a) Ta có 1 9  4.3
  0  3.3x   4.3x 1 0  3x   1 3.3x   1  0 3 x x 0 3 1  0 3  3 x  0      . 
Vậy phương trình có tập nghiệm là S  0;   1 . x x 1 3.3 1  0 3  3 x  1 2
b) Điều kiện: x  5. Ta có log x  6x  9  log 5  x  log
x  3  log 5  x 4  4 2  2   2 2 2   2   x   log  1 2
x  3  log 5  x 2 2
x  3  5  x x x  2  0  (tmđk). 2 2  x   2
Vậy phương trình có tập nghiệm là S  1;   2 .
Bài 3 (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật và AD  2a,
CD a 2. Biết SA vuông góc với mặt phẳng  ABCD và SA  3a 2. Gọi K là trung điểm của đoạn A . D
a) Tính thể tích khối chóp S.BCK theo . a
b) Tính khoảng cách giữa hai đường thẳng SB, AD theo . a
c) Chứng minh rằng SBK  vuông góc với SAC.
Lời giải. a) Ta có 2 SSSSa 2.  BKC ABCDABKKCD S
Suy ra thể tích khối chóp S.BCK là 1 1 2 3 V  .S . A S
 .3a 2.a 2  2a (đvtt). S.BCK 3  BCK 3
b) Vì AD // BC AD // SBC  d  ;
SB AD  d  ; A SBC H K D
Kẻ AH vuông góc với SB H SB  AH  SBCA 1 1 1
Tam giác SAB vuông tại , A có   B C 2 2 2 AH SA AB . SA AB 3a 2.a 2 3a Suy ra d S ; B AD    . 2 2 SA AB
a 2 a 2 5 3 2 2          
c) Ta có AC.BK   AB AD.BABD   AB AD.2 AB AD
2   2
  AB AB AD AD AD AB   a2 2 2 2 . 2 2
 2.a 22  0.  
Suy ra AC.BK  0  AC BK mà SA BK BK  SAC  SBK   SAC.
Bài 4 (1,0 điểm). Cho a, b, c là các số thực dương. Tìm giá trị lớn nhất của biểu thức 4 9 P   . 2 2 2
a b c  4 a b a  2cb  2c
Lời giải. Áp dụng bất đẳng thức AM – GM, ta có 2 2          
cb c  a ba b 4c a b 2ab 4ac 4bc a b a 2 2 .   2 2 2 2
a b c . 2 2 4 9 Đặt 2 2 2
t a b c  4, suy ra t  2 và P   t 2 . 2 t  4 4 9 4 9t
Xét hàm số f t  
với t  2. Ta có f t     0  t  4. t 2 2t  4 2 t  2t 42 5
Tính các giá trị f 4  ; lim f t   và lim f t  0. 2 8 t t 4 5
Suy ra giá trị lớn nhất của hàm số f t là . Dấu "  " xảy ra  a b c  2. 8 5
Vậy giá trị nhỏ nhất của biểu thức P là . 8