


Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ 1 QUẬN TÂN PHÚ
Năm học 2019 – 2020 Môn Toán – Lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Bài 1: (1 điểm) Điền ký hiệu ; ;
hoaëc vào ô vuông để có phát biểu đúng: 2019 N; Z Q; 6 Q; 4 N
Bài 2: (3,5 điểm) Tính giá trị x, biết: 3 1 5 2 1 2 a) .x
b) 1 x 2 2 2 6 3 19 5 1 5 25 3 12 4 14 20 .8 .3 c) x . . . d) x 11 14 11 7 4 11 13 36 15 .2
Bài 3: (1,0 điểm) Tổng số học sinh tham gia Câu lạc bộ “Đàn dân tộc” của ba
lớp 7A, 7B và 7C là 90 học sinh. Biết số học sinh tham gia Câu lạc bộ của mỗi
lớp 7A, 7B và 7C lần lượt tỉ lệ với 16; 15 và 14. Hỏi mỗi lớp có bao nhiêu học
sinh tham gia câu lạc bộ trên?
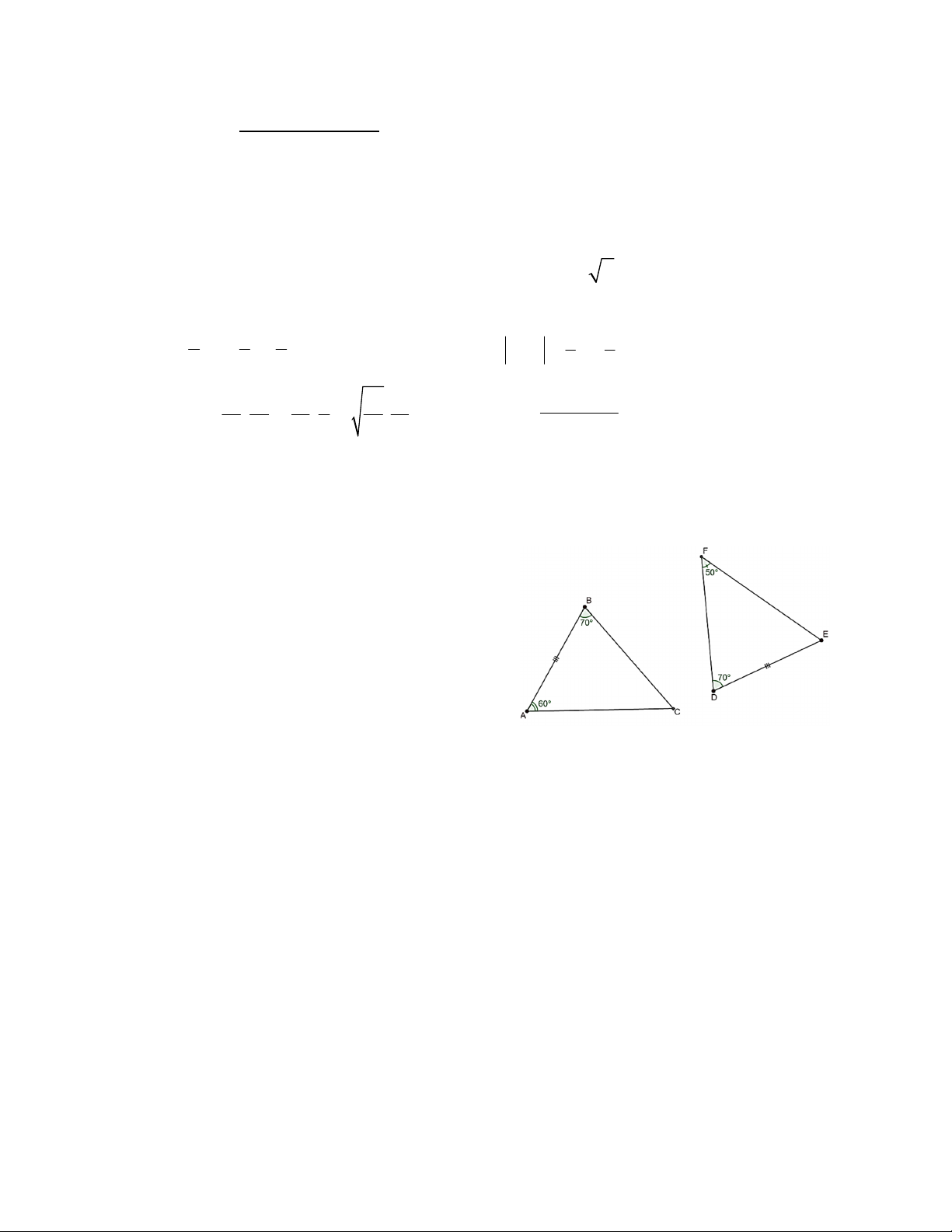
Bài 4: (1,0 điểm) Cho hình vẽ bên (học
sinh không cần vẽ lại hình khi làm bài).
a) Tính số đo của góc DEF.
b) Hai tam giác trong hình có bằng nhau không? Giải thích.
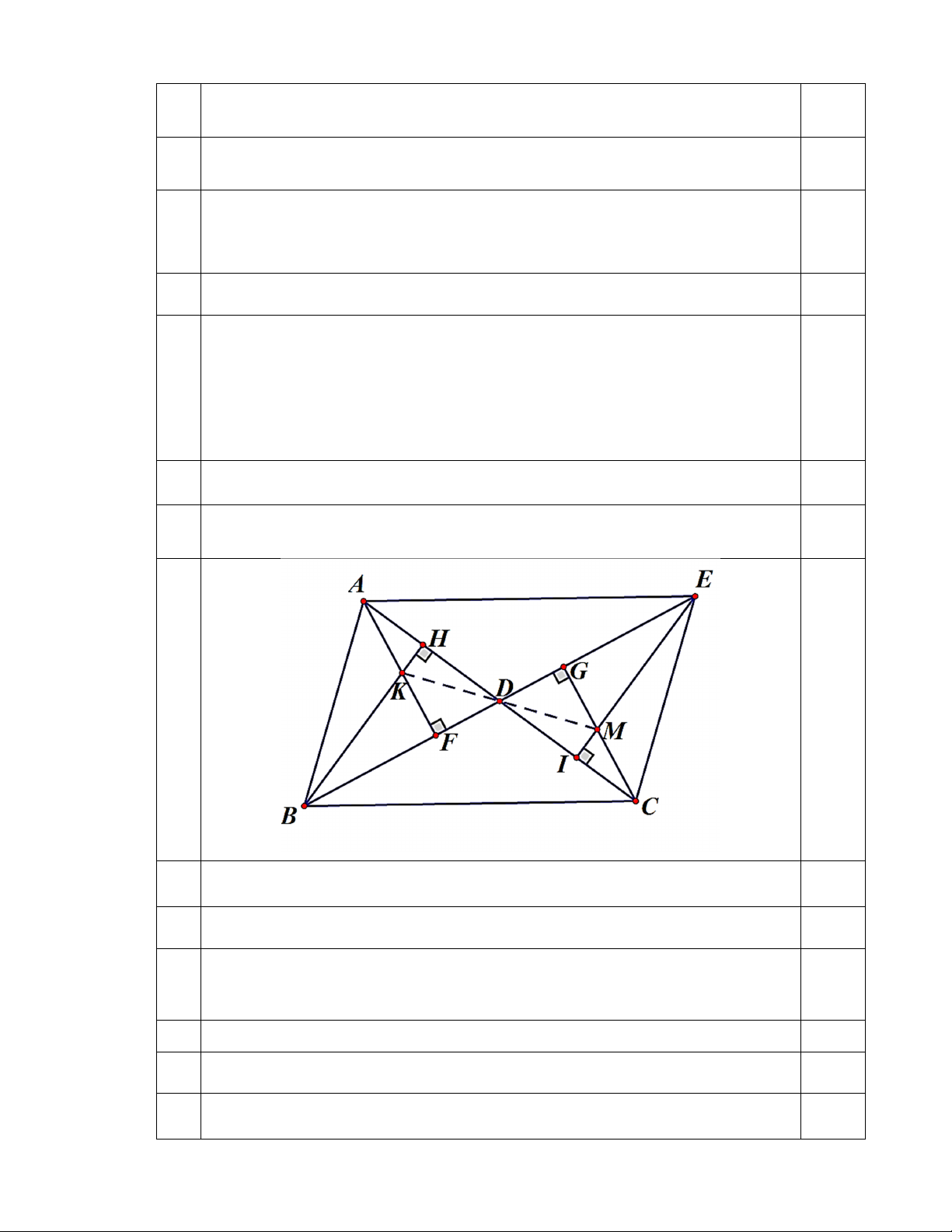
Bài 5: (2,5 điểm) Cho tam giác nhọn ABC (AB < AC). Gọi D là trung điểm của
cạnh AC. Trên tia đối của tia DB lấy điểm E sao cho DE = DB.
a) Chứng minh △ABD = △CED. Suy ra AB song song với CE.
b) Kẻ AF vuông góc với BD tại F và CG vuông góc với DE tại G. Chứng minh
AF song song với CG và DF = DG.
c) Kẻ BH vuông góc với AD tại H và EI vuông góc với DC tại I. Đoạn BH cắt
AF tại K. Đoạn CG cắt EI tại M. Chứng minh ba điểm K, D, M thẳng hàng.
Bài 6: (1,0 điểm) Mẹ của An mang một số tiền vào siêu thị để mua hoa quả và
nhẩm tính rằng với số tiền trên có thể mua được 3kg lê, hoặc 4kg nho, hoặc 5kg
táo. Tính giá tiền mỗi loại hoa quả trên, biết 4kg nho đắt hơn 3kg táo là 240.000 đồng. - HẾT –
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KỲ 1 QUẬN TÂN PHÚ
Năm học 2019 – 2020 Môn Toán – Lớp 7
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Thầy (cô) chấm bài theo khung điểm định sẵn (học sinh không được làm tắt các
bước trình bày bằng cách sử dụng máy tính cầm tay). Nếu học sinh làm cách khác,
nhóm Toán của trường thống nhất dựa trên cấu trúc thang điểm của hướng dẫn chấm. Hướng dẫn chấm Điểm
Bài (1 điểm) Điền ký hiệu ; ;
hoaëc vào ô vuông để có phát biểu đúng: 1: 2019 N; Z Q; 6 Q; 4 N 1
Bài (3,5 điểm) Tính giá trị x, biết: 2: a) 3 1 5 .x 2 2 2 3 5 1 0,25 x 2 2 2 3 0,5 x 2 2 3 2 4 0,25 x 2 : 2. 2 3 3 . b) 2 1 2 1x 6 3 4 1 0,5 1 x 9 6 11 1 x 18 x 11 x 11 1 hoaëc 1 18 18 7 29 0,5 Tính được x hoaëc x . 18 18 c) 19 5 1 5 25 3 x . . . 11 14 11 7 4 11 19 5 1 5 5 3 0,25 x . . . 11 14 11 7 2 11 5 19 5 1 5 3 0,25 x . . . 11 14 11 7 11 2 5 19 1 3 0,25 x . 11 1 4 7 2 5 19 2 21 x . 11 14 14 14 5 0,25 x .0 0 11 d) 12 4 14 20 .8 .3 x 13 36 15 .2 2 . 12 5 .2 4 2 3 14 .3 0,25 3. 13 36 5 .2 24 12 12 14 2 .5 .2 .3 13 13 36 3 .5 .2 36 12 14 2 .5 .3 3 0,25 13 13 36 3 .5 .2 5
Bài (1,0 điểm) 3:
Gọi x, y, z lần lượt là số học sinh tham gia câu lạc bộ “Đàn dân tộc” của các * lớp 7A, 7B, 7C (x, ,
y z N ,0 x, , y z 90). Theo đề bài: 0,25 x y z = =
; x y z 90 16 15 14
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được 0,25 x y z
x y z 90 2 16 15 14 16 15 14 45 Do đó: 0,5 (đúng x
2 x 16.2 32 2/3 1 6 đáp y
2 y 15.2 30 số 1 5 được z
2 z 14.2 28 0,25). 1 4
Vậy số học sinh tham gia câu lạc bộ của các lớp 7A, 7B, 7C thứ tự là 32 học
sinh, 30 học sinh, 28 học sinh.
Bài (1,0 điểm) 4:
Cho hình vẽ (học sinh không cần vẽ lại hình khi làm bài). a) 0,25 Xét tam giác DEF có: 0
DEF EDF EFD 180 (định lý) 0 0 0
DEF 70 50 180 0,25 Tính được 0 DEF 60 . b) Xét A BC và E DF : 0,25 AB DE (gt) 0
B D 70 (gt) 0
A E 60 (cmt) Do đó, A BC E
DF g c g. 0,25
Bài (2,5 điểm) 5: a) Chứng minh được A DB C
DE c g c. 0,5 0,25
Suy ra BAD ECD . 0,25
Mà BAD và ECD so le trong Nên AB song song với CE. b)
Chứng minh được AF song song với CG (cùng vuông góc với BE). 0,25 0,25
Chứng minh được FAD GCD . Chứng minh được F AD G
CDg c g. Suy ra DF DG. 0,25 c)
Chứng minh được BH song song với EI (cùng vuông góc với AC). 0,25
Suy ra HBD IED .
Có: BF DB DF DE DG EG . Chứng minh được B KF E
MG g c gnên KF MG . 0,25 0,25 Chứng minh được K FD M
GDc g cnên FDK GDM . Mà 0
FDK EDK 180 (kề bù). Suy ra 0
GDM EDK 180 . Vậy K, D, M thẳng hàng.
Bài (1,0 điểm) 6:
Gọi x, y, z (đơn vị: đồng) lần lượt là giá tiền của mỗi kg lê, nho, táo (x,y, z dương).
Theo đề: 3x 4y 5z và 4y 3z 240000 0,25 3x 4y 5z Suy ra
và 4y 3z 240000 60 60 60
Áp dụng tính chất dãy tỉ số bằng nhau: 0,5 x y z 4y 3z 240000 10000 . 20 15 12 4.15 3.12 24
Suy ra x 200000 ; y 150000 ; z 120000 . 0,25
Vậy mỗi kg lê giá 200000 đồng, mỗi kg nho giá 150000 đồng, mỗi kg táo giá 120000 đồng.




