Đề thi học kì 1 môn Toán 7 | Đề 6 | Cánh diều

A. KHUNG MA TRẬN BÀI ĐÁNH GIÁ CUỐI KÌ 1 TOÁN – LỚP 7 Nội
Mức độ đánh giá Tổng Chủ dung/Đơn Nhận biết Thông hiểu Vận dụng Vận dụng cao TT đề % vị kiến TNKQ TL TNKQ TL TNKQ TL TNKQ TL điểm thức Số hữu tỉ 2 và tập hợp (TN1,2,) các số hữu 0,5đ Số
tỉ. Thứ tự hữu trong tập 1 tỉ, số hợp các số 67,5% thực hữu tỉ Các phép 3 3 5 1 tính với (TN3,11,12) (TL1a,2a,b) (TL (TL5) số thực 0,75đ 1,5đ 1,b,c,d;2c;3) 0,5đ 3,5đ Hình hộp 1 chữ nhật (TN7) Các và hình 0,25đ 12,5% hình lập khối phương 2 trong Lăng trụ 3 thực
đứng tam (TN4,5,6,8) tiễn giác, lăng 1đ trụ đứng tứ giác Góc ở vị 1 2 1 Góc trí đặc (TL4a) (TN9,10) (TL 4b) 20% và 3 1đ 0,5 đ 0,5đ đườ biệt. Tia ng phân giác thẳng của một 1 song góc. Hai song đường thẳng song song Tổng: Số câu 6 1 5 3 6 1 Điểm 1,75đ 1đ 1.25 đ 1,5đ 4đ 0,5đ 10 Tỉ lệ % 27,5% 27,5% 40% 5% 100% Tỉ lệ chung 55% 45% 100%
B. BẢN ĐẶC TẢ MA TRẬN BÀI ĐÁNH GIÁ CUỐI HỌC KÌ 1 TOÁN – LỚP 7 TT Chương/Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức Nhận biết Thông Vận Vận hiểu dụng dụng cao ĐAI SỐ 1 Số hữu Nhận biết: tỉ
– Nhận biết được số hữu tỉ và lấy được ví dụ về số hữu tỉ.
Số hữu tỉ và
tập hợp các số
hữu tỉ. Thứ tự
trong tập hợp
các số hữu tỉ 1TN
– Nhận biết được tập hợp các số hữu tỉ. 2 – 1TN
Nhận biết được số đối của một số hữu tỉ.
– Nhận biết được thứ tự trong tập hợp các số hữu tỉ. Các phép 3TN 1TL Thông hiểu:
tính với số 3TL hữu tỉ
– Mô tả được phép tính luỹ thừa với số mũ tự nhiên
của một số hữu tỉ và một số tính chất của phép tính
đó (tích và thương của hai luỹ thừa cùng cơ số, luỹ thừa của luỹ thừa).
– Mô tả được thứ tự thực hiện các phép tính, quy tắc
dấu ngoặc, quy tắc chuyển vế trong tập hợp số hữu tỉ. Vận dụng: 4TL
– Thực hiện được các phép tính: cộng, trừ, nhân,
chia trong tập hợp số hữu tỉ. – Vận dụng được các
tính chất giao hoán, kết hợp, phân phối của phép
nhân đối với phép cộng, quy tắc dấu ngoặc với số
hữu tỉ trong tính toán (tính viết và tính nhẩm, tính
nhanh một cách hợp lí).
Tỉ lệ thức và Vận dụng: 1TL dãy tỉ số
- Vận dụng được tính chất của tỉ lệ thức trong giải bằng nhau toán. 3
- Vận dụng được tính chất của dãy tỉ số bằng nhau trong giải toán. HÌNH HỌC 2 Các Hình hộp Nhận biết: hình
chữ nhật và
Mô tả được một số yếu tố cơ bản (đỉnh, cạnh, góc, 1TN khối hình lập
đường chéo) của hình hộp chữ nhật và hình lập trong phương phương. thực tiễn Thông hiểu
– Giải quyết được một số vấn đề thực tiễn gắn với
việc tính thể tích, diện tích xung quanh của hình
hộp chữ nhật, hình lập phương (ví dụ: tính thể tích
hoặc diện tích xung quanh của một số đồ vật quen
thuộc có dạng hình hộp chữ nhật, hình lập phương,…). Nhận biết 4TN
– Mô tả được một số yếu tố cơ bản (cạnh, góc, Lăng trụ
đường chéo) của hình chữ nhật, hình thoi, hình
đứng tam
bình hành, hình thang cân.
giác, lăng trụ Thông hiểu:
đứng tứ giác – Mô tả được một số yếu tố cơ bản (cạnh, góc,
đường chéo) của hình chữ nhật, hình thoi, hình
bình hành, hình thang cân. Vận dụng :
– Giải quyết được một số vấn đề thực tiễn (đơn
giản) gắn với việc tính chu vi và diện tích của các
hình đặc biệt nói trên. 3 Góc và
Góc ở vị trí 1TL 2
Nhận biết : đường
đặc biệt. Tia TN 4 thẳng phân giác
– Nhận biết được các góc ở vị trí đặc biệt (hai song
của một góc. góc kề bù, hai góc đối đỉnh). song Hai đường thẳng song song –
Nhận biết được tia phân giác của một góc.
– Nhận biết được cách vẽ tia phân giác của một
góc bằng dụng cụ học tập Vận dụng: 1TL
- Mô tả được dấu hiệu song song của hai đường
thẳng thông qua cặp góc so le trong. 5 C. ĐỀ MINH HỌA
PHẦN 1. TRẮC NGHIỆM KHÁCH QUAN. (3,0 điểm)
Hãy khoanh tròn vào phương án đúng trong mỗi câu dưới đây:
Câu 1. Tập hợp các số hữu tỉ kí hiệu là: A. B. * C. D. 2 −
Câu 2. Số đối cùa là: 3 2 3 3 − 2 A. B. C. D. 3 2 2 3 − 3 2
Câu 3. Giá trị của (0,5) : (0,5) bằng: A. ( )6 0, 5 ; B. ( )5 0, 5 ; C. 0, 5 ; D. 1
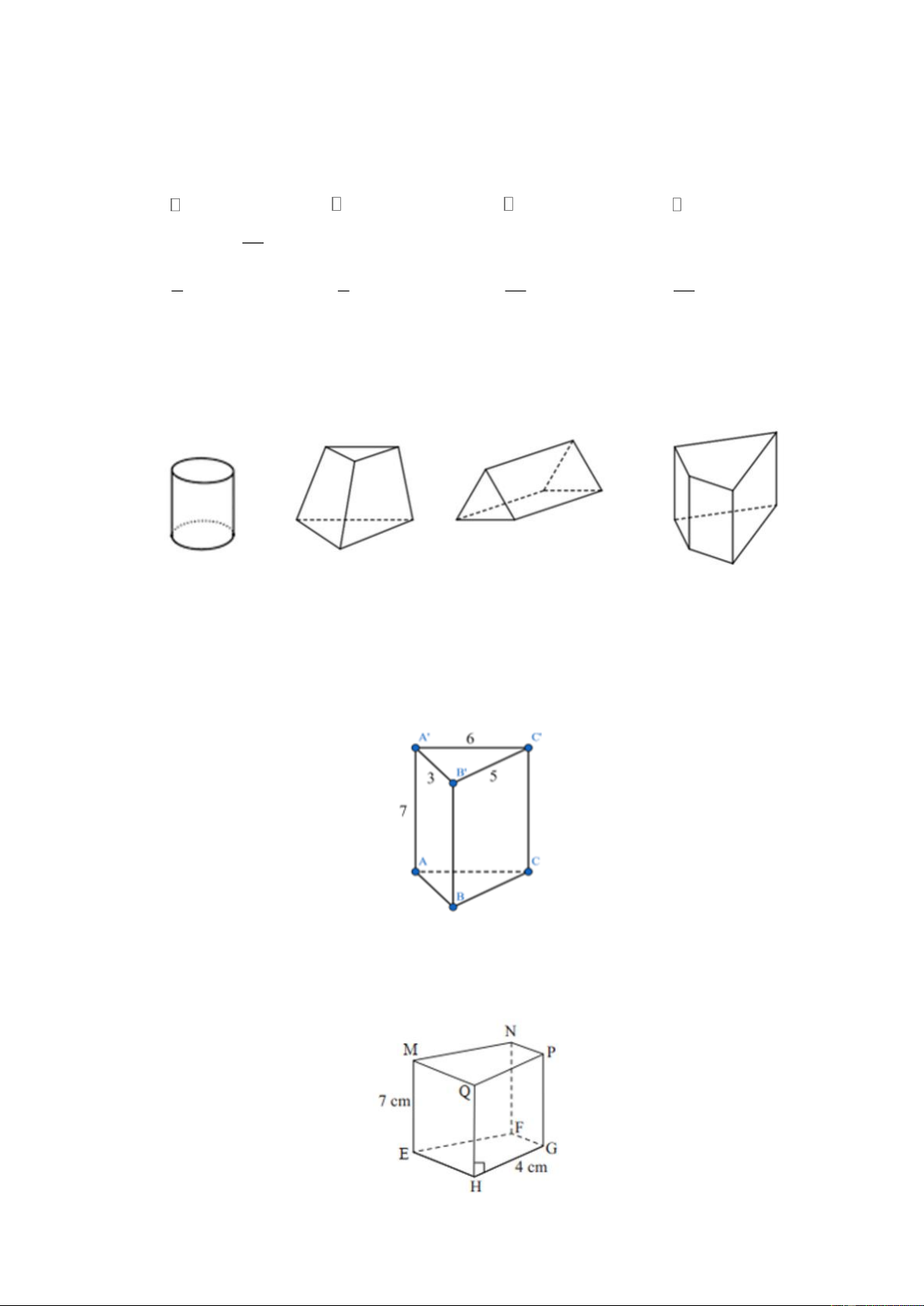
Câu 4. Trong các hình sau, hình nào là hình lăng trụ đứng tam giác? Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 1 B. Hình 2 C. Hình 3 D. Hình 4
Câu 5. Cho hình lăng trụ đứng tam giác AB .
C A' B 'C ' có cạnh A' B ' = 3cm , B 'C ' = 5cm ,
A'C ' = 6cm , AA' = 7cm . Độ dài cạnh BC sẽ bằng: A. 3cm B. 5cm C. 6cm D. 7cm
Câu 6. Cho hình lặng trụ đứng tứ giác như hình bên. Khẳng định nào sau đây là sai? 6 A. QH = 7cm B. QP = 4cm C. Mặt đáy là EFGH D. MQ = 7cm
Câu 7. Hình hộp chữ nhật có số đỉnh là: A. 6 B. 8 C. 10 D. 12
Câu 8. Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể
tích của hình lăng trụ đứng là gì? 1
A. V = S.h; B. V = S.h 2 C. V = 2S.h D. V = 3S.h
Câu 9. Hai đường thẳng xx’ và yy’ cắt nhau tại O. Góc đối đỉnh của góc xOy ' là: A. x 'Oy ' B. x 'Oy C. xOy D. y 'Ox
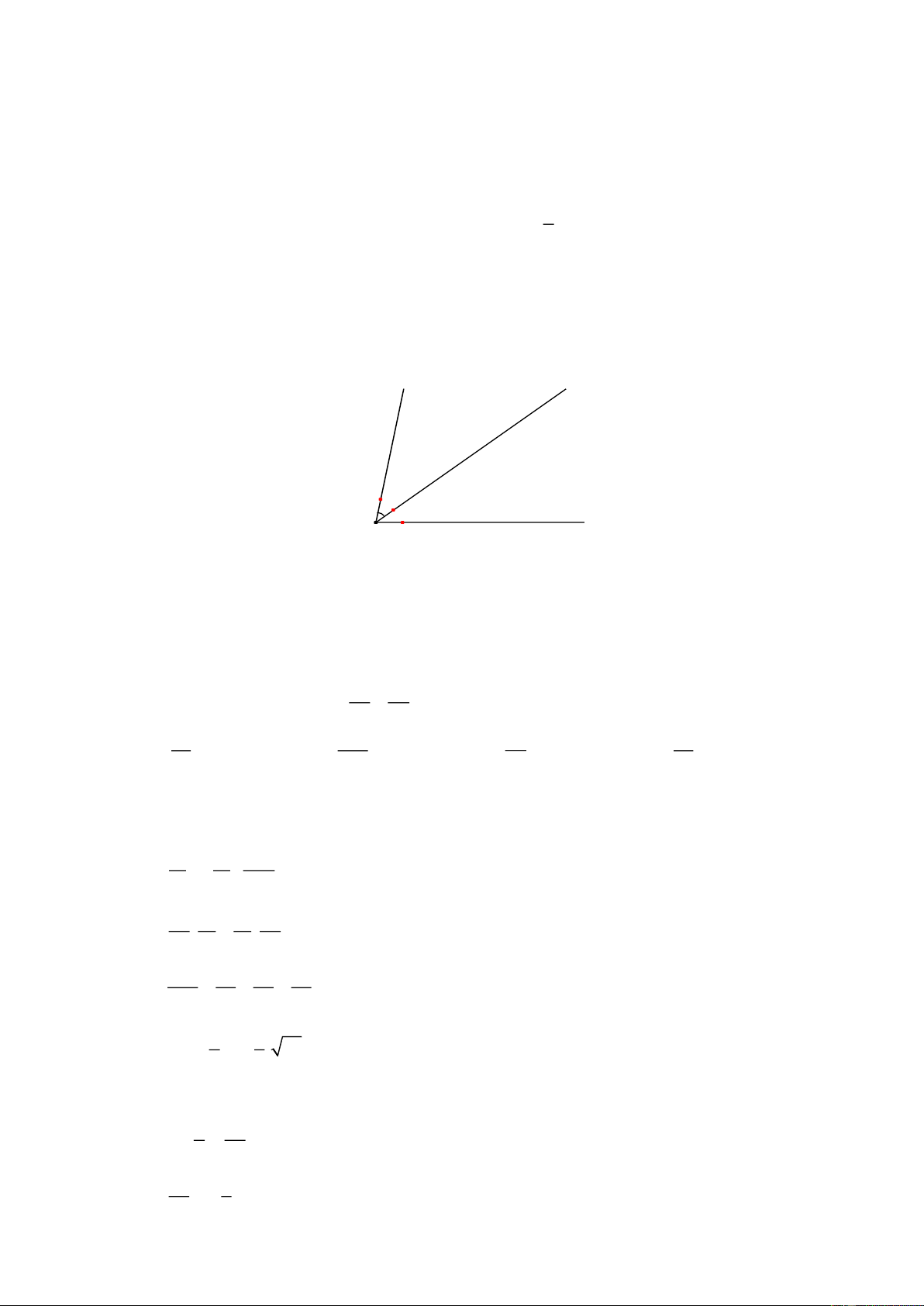
Câu 10. Cho hình vẽ, biết 40o xOy =
, Oy là tia phân giác của góc xOz . Khi đó số đo yOz bằng: x y O z A. 20o B. 140o C. 80o D. 40o
Câu 11. Kết quả của phép tính 2 5 2 .2 là: A. 10 2 B. 3 2 C. 5 2 D. 7 2 3 − 2 −
Câu 12. Kết quả của phép tính + là: 20 15 1 − −17 5 − 1 − A. B. C. D. 35 60 35 60
PHẦN 2: TỰ LUẬN (7,0 điểm)
Câu 1. (2 điểm) Tính: 3 4 3 − a) + . 7 7 4 5 − 4 9 5 − b) . + . 17 13 13 17 2 − 0 4 20 33 c) + − + + 0,5 41 37 41 37 2  3  1 d) 3 : − + . 36    2  9
Câu 2. (1,5 điểm) Tìm x biết: 2 5 − a) x + = 9 12 3 − 1 b) .x − = 0,25 4 5 7 1 c) x + =1,5 2
Câu 3. (1,5 điểm) Ba lớp 7A, 7B, 7C có số học sinh giỏi lần lượt tỉ lệ với 2; 4; 6. Tính số học
sinh giỏi của mỗi lớp biết tổng số học sinh giỏi của khối 7 là 48 học sinh.
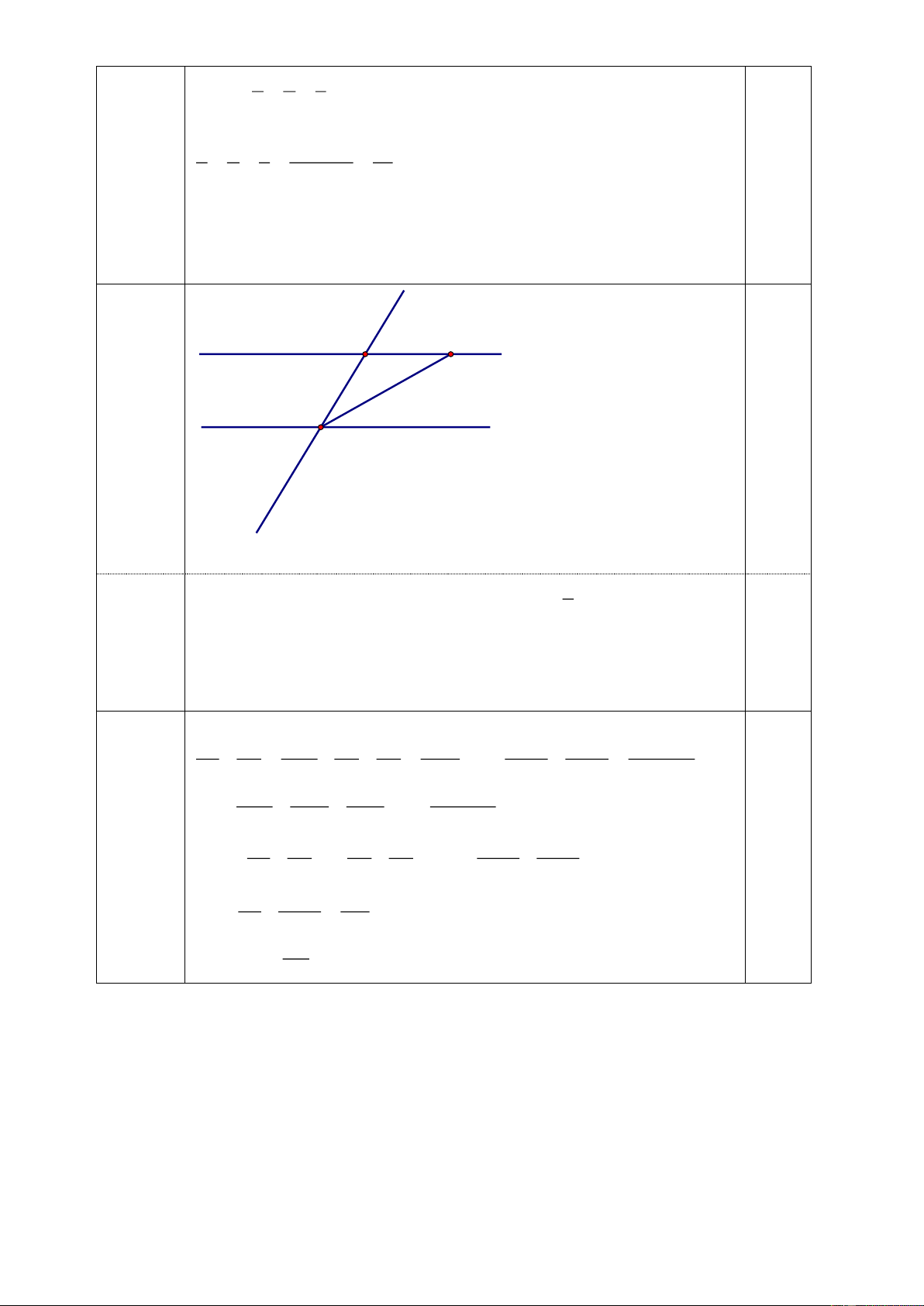
Câu 4. (1,5 điểm) Cho đường thẳng xy cắt đường thẳng ab tại O sao cho 60o xOa = . a) Tính số đo góc bOy.
b) Trên tia Oa lấy điểm C sao cho C khác O. Từ C vẽ đường thẳng d song song với xy.
Vẽ tia Ot là tia phân giác của góc xOa cắt đường thẳng d tại P. Tính số đo góc OPd. 1 1 1 1
Câu 5. (0,5 điểm) Tính tổng: B = + + +...+ . 1.2.3 2.3.4 3.4.5 37.38.39
--------------- HẾT --------------- 8
D. ĐÁP ÁN VÀ THANG ĐIỂM
I. TRẮC NGHIỆM: (3,0 điểm) Mỗi phương án chọn đúng ghi 0,25 điểm. Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đ/án C A C B B D B A B A D B
II. TỰ LUẬN: (7,0 điểm) Bài Lời giải Điểm 1a 3 4 3 − 3 3 − + = + = 0,5 (0,5đ) a) . 0 7 7 4 7 7 b 5 − 4 9 5 − 5 −  4 9  5 − 0, 5 (0,5đ) + = + = b) . . .  17 13 13 17 17 13 13  17 c 2 − 0 4 21 33  2 − 0 21  4 33  0,5 c) + − + + 0,5 = − + + + 0,5 = 0,5 (0,5đ)     41 37 41 37  41 41  37 37  d 2  3  1 4 1 4 2 0,5 (0,5đ) d )3 : − + . 36 = 3. + .6 = + = 2    2  9 9 9 3 3 2a 2 5 − + = 0,5 (0, 5đ) a)x 9 12 5 − 2 x = − 12 9 23 − x = 36 b 3 − 1 − = 0,5 (0,5đ) b) .x 0, 25 4 5 3 − 1 1 .x = + 4 4 5 3 − 9 .x = 4 20 9 3 − x = : 20 4 3 − x = 5 c 1 0,5 (0,5đ) c) x + =1,5 2 1 3 1 3 x + = hoặc x + = − 2 2 2 2 3 1  3  1 x = − hoặc x = − −   2 2  2  2
x = 1 hoặc x = 2 − 3
Gọi số học sinh giỏi của ba lớp 7A, 7B, 7C lần lượt là x, y, z 0,25 (1,5đ) ( *
x, y, z  ). 0,25 9 x y z Ta có:
= = và x + y + z = 48 . 2 4 6 0,5
Áp dụng tính chất dãy tỉ số bằng nhau ta có: x y z x + y + z 48 = = = = = 4 . 2 4 6 12 12 0,25
Suy ra x = 2.4 = 8 (học sinh), y = 4.4 = 16 (học sinh), z = 4.6 = 24 (học sinh). 0,25
Vậy số học sinh ba lớp 7A, 7B, 7C lần lượt là 8 học sinh, 16 học sinh, 24 học sinh. 4a a 0,25 (0,75đ) C d P y O x b
a) Vì xOa và bOy là hai góc đối đỉnh nên = = 60o bOy xOa . 0,5 b 1 o = = 0,25 (0,75đ)
b) Vì OP là tia phân giác góc xOa nên xOP xOa 30 . 2
Vì đường thẳng d song song với đường thẳng xy nên 0,25 = = 30o OPC xOP . 0,25 Khi đó =180o − =150o OPd OPC (hai góc kề bù). 5 Ta có: (0,5đ) 1 1 2 1 1 2 1 1 2 − = 0,25 ; − = ; ....; − = . 1.2 2.3 1.2.3 2.3 3.4 2.3.4 37.38 38.39 37.38.39 2 2 2 2 2B = + + +...+ 1.2.3 2.3.4 3.4.5 37.38.39 0,25  1 1   1 1   1 1  = − + − +...+ −       1.2 2.3   2.3 3.4   37.38 38.39  1 1 370 = − = . 1.2 38.39 741 185 Suy ra B = . 741 10