Đề thi học kì 1 Toán 10 năm 2019 – 2020 trường THPT Trần Văn Giàu – TP HCM

Để giúp các em đạt được điểm số cao trong kì thi HK1 Toán 10 sắp tới, xin chia sẻ đến các em đề thi học kì 1 Toán 10 năm học 2019 – 2020 trường THPT Trần Văn Giàu, thành phố Hồ Chí Minh, mời bạn đọc đón xem

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Câu 1: ( 1 điểm) Tìm tập xác định của hàm số:
a) y =
2
4
32
xx
x
b)
2
8 3 3 4
1
x x
y
x
Câu 2: ( 2 điểm) Giải các phương trình sau:
a)
2
6x 4x 3 3x 4
b) .
Câu 3: (1 điểm)
Khảo sát và vẽ đồ thị hàm số
2
Câu 4: ( 1 điểm)
Tìm
2
: 2
P y ax x c
, biết đồ thị (P) đi qua điểm
2; 5
A
và cắt trục tung tại
điểm B có tung độ là 3.
Câu 5: (1 điểm)
Cho phương trình: x
2
– 2(m – 1)x + m
2
+ 4 = 0. Xác định m để phương trình có hai
nghiệm x
1
, x
2
thỏa mãn
1 2
2 1
3
x x
x x
Câu 6: (1 điểm)
Cho
2
x
. Tìm giá trị nhỏ nhất của hàm số
6
3
2
y x
x
Câu 7: (2 điểm)
Trong hệ trục tọa độ
Oxy
, cho
3; 2 , 1; 4 , 2;5
A B C
a) Tính
.
AB BC AC
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
c) Trên trục
Ox
, tìm tọa độ điểm M sao cho tam giác ABM cân tại M.
Câu 8: (1 điểm)
Cho tam giác ABC, lấy D là điểm đối xứng của B qua C và M là trung điểm AC.
Phân tích véctơ
DM
theo hai véctơ
; .
AB AC
---HẾT---
Ghi chú: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì
thêm.
3 2 1
x x
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
TRƯỜNG THPT
TRẦN VĂN GIÀU
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC 2019 – 2020
MÔN TOÁN - LỚP 10 CƠ BẢN
Hình thức: Tự luận
Thời gian: 90 phút
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
TRƯỜNG THPT TRẦN VĂN GIÀU
==== o O o ====
ĐÁP ÁN ĐỀ THI HỌC KÌ I
NĂM HỌC 2019 -2020
MÔN TOÁN, LỚP 10
Thời gian làm bài: 90 phút
Bài Đáp án Điểm
1a
2
2
2 3
4
: 4 0
x
y
x x
ÐK x x
0,25
0
4
: \ 0;4
x
x
TXÐ D
0,25
1b
2
2
8 3 3 4
1
8 0
: 3 4 0
1 0
x x
y
x
x
ÐK x
x
0,25
8
4
3
4
: ;8
3
x
x
TXÐ D
0,25
2a
2
2
6 4 3 3 4
3 4 0
6 4 3 3 4
x x x
x
x x x
0,5
2
4
3
6 1 0
x
x x
0,25
4
3
1
1
2
1
2
1
3
3
x
x
x
x
x
0,25
2b.
3 2 1
3 0
: 2 3
2 0
x x
x
ÐK x
x
0,25
3 2 1 2 2x x x
0,25
2
2
0
2 0
x x
x
x x
0,25
0
1
1
2
x
x
x
x
0,25
3
Khảo sát và vẽ đồ thị hàm số:
2
4 3y x x
Tập xác định:
D
Tọa độ đỉnh
2; 1I
0,25
Trục đối xứng
2x
0,25
Bảng giá trị:
x
0
1
2
3
4
y
3
0
1
0
3
0,25
V
ẽ:
0,25
4
2
2P y ax x c
đi qua
2; 5 : 5 4 4A a c
0,25
P
cắt trục tung tại điểm B có tung độ là 3:
3c
0,25
4 1
1
3
a c
a
c
0,25
2
: 2 3P y x x
0,25
5
' 2 3
m
Phương trình có hai nghiệm
1 2
0
3
;
' 0
2
a
x x m
0,25
Theo định lí Vi-et:
1 2
2
1 2
2 1
4
x x m
x x m
0,25
2
1 2
2 1
3 8 16 0
x x
m m
x x
0,25
4
m
( nhận )
0,25
6
Áp dụng bất đẳng thức Co-si cho hai số:
6
3 2 0; 0
2
x
x
6 6
3 2 2 3 2
2 2
x x
x x
0,25
6
3 6 6 2
2
x
x
.
0,25
6
3 6 2 6
2
x
x
Vậy giá trị nhỏ nhất của hàm số là
6 2 6
0,25
GTNN khi
6
3 2
2
2 2
2 2
x
x
x n
x l
0,25
7a
2; 2
1;9
1;7
AB
BC
AC
.
0,25
32
AB BC AC
0,25
7b
Gọi
;
D x y
2 ;5
DC x y
0,25
ABCD là hình bình hành
2 2
5 2
x
AB DC
y
0,25
4
7
x
y
.
0,25
7c
;0
M Ox M x
3;2
1;4
AM x
BM x
0,25
2 2
3 4 1 16
AM BM x x
0,25
1
x
Vậy
1;0
M
0,25
8
DM DC CM
0,25
1
2
CB CA
0,25
1
2
AB AC AC
0,25
3
2
AB AC
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019 – 2020 TRƯỜNG THPT
MÔN TOÁN - LỚP 10 CƠ BẢN TRẦN VĂN GIÀU Hình thức: Tự luận Thời gian: 90 phút
Câu 1: ( 1 điểm) Tìm tập xác định của hàm số: 2x  3 8  x  3 3x  4 a) y = b) y  2 4x  x 2 x 1
Câu 2: ( 2 điểm) Giải các phương trình sau: a) 2     6x 4x 3 3x 4 b) 3  x  x  2 1. Câu 3: (1 điểm)
Khảo sát và vẽ đồ thị hàm số 2 y  x  4x  3 Câu 4: ( 1 điểm) Tìm P 2
: y  ax  2x  c , biết đồ thị (P) đi qua điểm A 2  ; 5
  và cắt trục tung tại
điểm B có tung độ là 3. Câu 5: (1 điểm)
Cho phương trình: x2 – 2(m – 1)x + m2 + 4 = 0. Xác định m để phương trình có hai x x nghiệm x1, x2 thỏa mãn 1 2   3 2 x 1 x Câu 6: (1 điểm) 6
Cho x  2 . Tìm giá trị nhỏ nhất của hàm số y  3x  x  2 Câu 7: (2 điểm)
Trong hệ trục tọa độ Oxy , cho A3; 2  , B1; 4  ,C2;5
   a) Tính A . B BC  AC
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
c) Trên trục Ox , tìm tọa độ điểm M sao cho tam giác ABM cân tại M. Câu 8: (1 điểm)
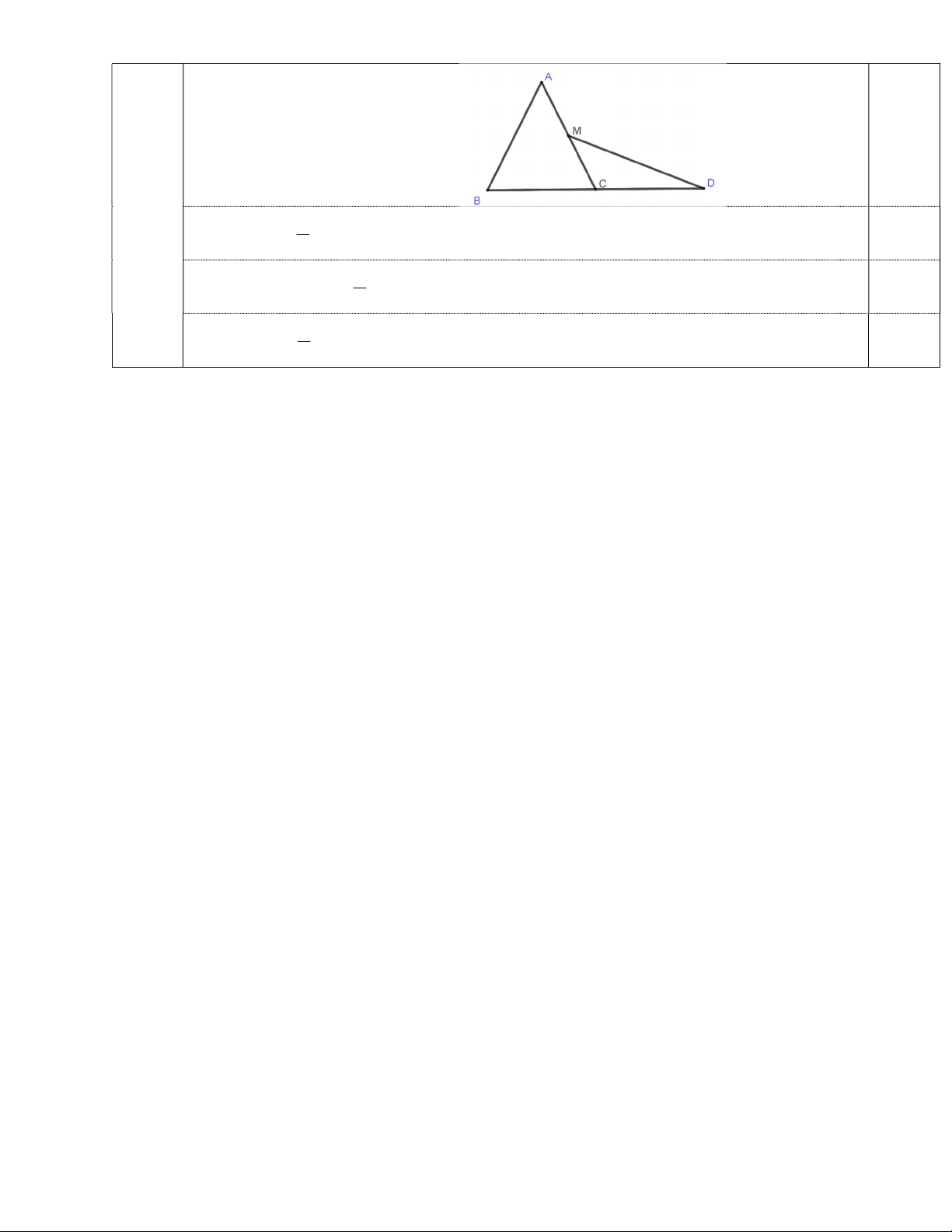
Cho tam giác ABC, lấy D là điểm đối xứng của B qua C và M là trung điểm AC.   
Phân tích véctơ DM theo hai véctơ AB; AC. ---HẾT---
Ghi chú: Học sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm.
SỞ GIÁO DỤC & ĐÀO TẠO TP.HCM
ĐÁP ÁN ĐỀ THI HỌC KÌ I
TRƯỜNG THPT TRẦN VĂN GIÀU NĂM HỌC 2019 -2020 ==== o O o ==== MÔN TOÁN, LỚP 10
Thời gian làm bài: 90 phút Bài Đáp án Điểm 1a 2x  3 y  2 4x  x 0,25 2 ÐK : 4x  x  0 x  0  x  4 0,25 TX : Ð D   \0;  4 1b 8  x  3 3x  4 y  2 x 1 8   x  0 0,25  ÐK : 3  x  4  0  2 x 1  0 x  8    4 x    3 0,25  4  TX : Ð D   ;8  3    2a 2 6x  4x  3  3x  4 3  x  4  0 0,5   2
6x  4x  3  3x  4  4 x     3 0,25 2 6x  x 1 0  4 x    3  1  x   1   2   x      0,25 2 1    x   1    3 x    3 2b. 3  x  x  2 1 3   x  0 0,25 ÐK :  2  x  3 x  2  0
3  x  x  2 1 2 x  2 0,25  x  2  x x  0 0,25   2 x  x  2  0 x  0 
 x  1  x  1  0,25  x  2 3 2
Khảo sát và vẽ đồ thị hàm số: y  x  4x  3 Tập xác định: D   0,25
Tọa độ đỉnh I 2;  1 Trục đối xứng x  2 0,25 Bảng giá trị: x 0 1 2 3 4 0,25 y 3 0 1  0 3 0,25 Vẽ: 4 P 2
y  ax  2x  c đi qua A 2  ; 5
  :5  4a  4  c 0,25
P cắt trục tung tại điểm B có tung độ là 3: c 3 0,25 4a  c  1    a  1  0,25 c  3 P 2 : y  x  2x  3 0,25 5 '  2  m 3 a  0 3
Phương trình có hai nghiệm x ; x    m   0,25 1 2 '  0 2 x   x  2 m 1 1 2   Theo định lí Vi-et:  0,25 2 x x  m  4  1 2 x x 1 2 2 
 3  m  8m 16  0 0,25 x x 2 1  m  4  ( nhận ) 0,25 6 3 x  2 6  
Áp dụng bất đẳng thức Co-si cho hai số: 0; 0 x  2  0,25 x   6   x   6 3 2 2 3 2 x  2 x  2 6 3x  6   6 2 . 0,25 x  2 6 3x   6 2  6 x  2 0,25
Vậy giá trị nhỏ nhất của hàm số là 6 2  6 x   6 3 2  x 2 GTNN khi x  2  2 n 0,25  x  2 2  l  7a AB  2;2  BC  1;9 . 0,25  AC  1;7
   ABBC  AC  3  2 0,25 7b Gọi D ; x y  0,25 DC  2  ; x 5  y   2  x  2    ABCD là hình bình hành AB DC 5   y  2 0,25 x  4   . 0,25 y  7 7c M Ox  M  ; x 0  AM   x  3;2 0,25  BM   x 1;4
AM  BM   x  2    x  2 3 4 1 16 0,25  x  1  Vậy M  1  ;0 0,25
   8 DM  DC  CM 0,25  1   CB  CA 0,25 2
  1   AB  AC  AC 0,25 2  3   AB  AC 0,25 2