Đề thi học kì 1 Toán 10 năm 2021 – 2022 trường THPT Nguyễn Gia Thiều – Hà Nội

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề thi học kì 1 Toán 10 năm 2021 – 2022 trường THPT Nguyễn Gia Thiều – Hà Nội. Đề thi 50 câu trắc nghiệm, thời gian học sinh làm bài thi là 90 phút,mời bạn đọc đón xem

26 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

8 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
TRƯỜNG THPT
NGUYỄN GIA THIỀU
ĐỀ CHÍNH THỨC
KIM TRA HỌC KÌ 1 NĂM HỌC 2021 – 2022
MÔN TOÁN – LỚP 10
Thời gian làm bài: 90 phút (không kể thời gian giao đề
H và tên hc sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho tập hp A v a l một phn t của tập hp A. Trong các mệnh đề sau, mệnh đề nào sai?
A.
{a} A
. B.
{a} A
. C.
aA
. D.
A
.
Câu 2. Cho mệnh đề chứa biến
( ):Pn
“
2
1n −
chia hết cho 4 ” với
n
l số nguyên. Chn mệnh đề đng trong cc
mệnh đề sau:
A.
. B.
. C.
(4)P
. D.
(6)P
.
Câu 3. Mệnh đề phủ đnh của mệnh đề “Phương trnh
( )
2
0 0ax bx c a+ + =
vô nghiệm” l:
A. Phương trnh
( )
2
0 0ax bx c a+ + =
không có nghiệm.
B. Phương trnh
( )
2
0 0ax bx c a+ + =
có nghiệm.
C. Phương trnh
( )
2
0 0ax bx c a+ + =
có 2 nghiệm phân biệt.
D. Phương trnh
( )
2
0 0ax bx c a+ + =
có nghiệm kép.
Câu 4. Gi A l tập hp cc số thc không nh hơn 1 v B l tập hp cc số thc c gi tr tuyệt đối nh hơn 2. Tm
AB
A.
(1;2)AB=
. B.
[1;2)AB=
. C.
[1;2]AB=
. D.
( 2;1)AB = −
.
Câu 5. Cho
0;1;2;3;4 , 2;3;4;5;6 .AB==
Tập hp
( ) ( )
\\A B B A
bằng?
A.
5;6 .
B.
2;3;4 .
C.
1;2 .
D.
0;1;5;6 .
Câu 6. Hàm số no sau đây đồng biến trên khong
( )
0;+
.
A.
2
2 2021y x x= − +
. B.
yx=
. C.
2
yx=−
. D.
21yx= − −
.
Câu 7. Hàm số nào trong các hàm số sau c đồ th nhận Oy l trục đối xứng:
A.
2
13y x x= − +
. B.
11y x x= − + +
. C.
1
y
x
=
. D.
3
yx=
.
Câu 8. Cho hàm số
1
0
2
20
khi x
x
y
x khi x
−
=
+
. Tập xc đnh của hàm số là:
A. . B.
−x sao chox 2}
. C.
)
2;− +
. D.
\{2}
.
Câu 9. Trong cc quy tc sau, quy tc no không phi l một hm số?
A. Quy tc đt tương ứng mi số thc dương với căn bậc hai của n.
B. Quy tc đt tương ứng mi số thc với căn bậc ba của n.
C. Quy tc đt tương ứng mi số thc với bnh phương của n.
D. Quy tc đt tương ứng mi số thc dương với gi tr tuyệt đối của n.
Câu 10. Biết gi tr nh nhất của hm số
3 1 1y x x= − + +
l
a
b
với
*
( , ;( , ) 1)a b N a b=
. Tnh
ab+
.
A.
3
B.
5
C.
2
D.
7
Câu 11. Tìm
m
để đường thẳng
31yx=+
song song với đường thẳng
( )
( )
2
11y m x m= − + −
.
A.
2m =−
. B.
0m =
. C.
2m =
. D.
2m =
.
Câu 12. Cho parabol
( )
2
:P y ax bx c= + +
( )
0a
. Xét dấu hệ số
a
và biệt thức
khi
( )
P
ct trục hoành tại 2
điểm phân biệt v c đỉnh nằm phía trên trục hoành.
A.
0, 0.a
B.
0, 0.a
C.
0, 0.a
D.
0, 0.a
Câu 13. Tìm ta độ giao điểm hai parabol
2
1
2
2
y x x=−
và
2
9
2
2
yx= − +
là:
A.
5
1;
2

−


,
9 99
;
5 50
−



. B.
( )
3
4;16 , 1;
2
−

−


.
C.
3
1;
2
−



. D.
( ) ( )
2; 2 , 2;6−−
.
Câu 14. Giá tr nh nhất của hàm số
2
23y x x= + −
là:
A.
2−
. B.
21
8
−
. C.
25
8
−
. D.
3−
.
Câu 15. Cho hàm số
1y x x= + +
. Chn mệnh đề sai trong cc mệnh đề sau:
A. Hm số c tập xc đnh l .
B. Hm số đ cho l hm số l.
B. Hm số đồng biến trên
)
1;− +
C.
Hm số không đổi trên
( )
;1− −
Câu 16. Khi một qu bng đưc đ lên, n sẽ đạt đến độ cao no đ rồi rơi xuống đất. Biết rằng quỹ đạo của qu
bóng là một cung parabol trong mt phẳng với hệ ta độ Oxy, trong đ x l thời gian (tính bằng giây) kể t khi qu
bng đưc đ lên; y l độ cao (tính bằng mét) của qu bóng. Gi thiết rằng qu bng đưc đ t độ cao 1,0m. Sau đ
1 giây, qu bng đạt độ cao 3m v 2 giây sau khi đ lên, n ở độ cao 4m (xem hình vẽ sau). Hi sau bao lâu thì qu
bóng sẽ đạt đưc độ cao lớn nhất kể t khi đ lên (tnh chnh xc đến hàng phn trăm)?
A. 2,51. B. 2,50 C. 2,52. D.
2,53
.
Câu 17. Chn php biến đổi đng trong cc php biến đổi sau:
A.
x 2 x 3 2 x x 3− = − =
B.
2
2 ( 2)= − = −x x x x
C.
x(x 2)
2 x 2
x2
−
= =
−
D.
x
= 2
2
4x=
Câu 18. Điều kiện xc đnh của phương trnh
2
5
20
7
x
x
x
+
− + =
−
là :
A.
2x
B.
7x
C.
72x
D.
72x
Câu 19. Xt lời gii bi ton sau khi gii phương trnh:
22
22
13
( 1) ( 3) (1)
2 1 6 9 (2)
2 (3)
xx
xx
x x x x
x
− = −
− = −
− + = − +
=
Th lại ta thấy
2x =
không tha mn phương trnh đ cho. Vậy phương trnh đ cho vô nghiệm.
Hi lời gii trên đng hay sai. Nếu sai th sai ở bước no?
A. Lời gii đng. B. Sai ở bước 2 C. Sai ở bước 3 D. Sai ở bước 1
Câu 20. Phương trnh
3 1 3 1 0xx− − + =
có bao nhiêu nghiệm?
A. 0 B. 1 C. 2 D. Vô số.
Câu 21. Có bao nhiêu giá tr nguyên của tham số
m
thuộc
5;4
để phương trnh
22
4 5 2 0m x m m
có
nghiệm.
A.
2
. B.
9
. C.
10
. D.
11
.
Câu 22. Phương trnh
4 2 2
3 (2 1) 2. 1 0x m x m− + − + + =
(với
m
là tham số) có bao nhiêu nghiệm ?
A. Có 2 nghiệm. B. Có 3 nghiệm. C. Có 4 nghiệm. D. Vô nghiệm.
Câu 23. Phương trnh
2
00ax bx c a
có hai nghiệm cùng dấu khi và chỉ khi :
A.
0
0P

. B.
0
0P

. C.
0
0S

. D.
0
0S

.
Câu 24. Gi s phương trnh
22
2 1 0x m x m m
(
m
là tham số) có hai nghiệm là
12
;xx
. Tính giá tr biểu
thức
12
P x x
theo
m
.
A.
2Pm=
. B.
22Pm=+
. C.
1P =
. D.
1P =
Câu 25. Tm m để phương trình
2
2 4 5x x m− − =
có
2
nghiệm phân biệt.
A.
07m
. B.
7m
. C.
( )
7; {0}m +
. D.
( 7; )m − +
.
Câu 26. Cho parabol
( )
2
: 2 10P y x x= − −
v đường thẳng
: 10d y mx=−
. Tìm tổng tất c các giá tr của tham số
m
để
d
ct
( )
P
tại hai điểm phân biệt
,AK
sao cho diện tích tam giác
OAK
bằng
5
.
A.
2−
. B.
4−
. C.
1−
. D.
3−
.
Câu 27. Tổng các nghiệm của phương trình
2
42
2
xx
x
−+
−
=
2−x
là: A. 4 B. 3 C. 5 D. 2
Câu 28: Trong mt phẳng ta độ
Oxy
, giao điểm của hai đường thẳng
( ): 2 1d x y+ = −
và
( '):6 3 3d x y+ = −
là
A.
(3; 1).M −
B.
(1; 3).N −
C.
( 1;3).P −
D.
( 3;1).Q −
Câu 29: Trong các hệ phương trnh sau, hệ phương trnh no vô số nghiệm?
A.
7 16
7 16
xy
xy
+=
+ = −
. B.
4 3 5
3 4 3
xy
xy
−=
+=
. C.
35
2 6 10
xy
xy
− = −
− + =
. D.
6 3 1
8 4 1
xy
xy
− = −
− + = −
.
Câu 30: Xét hệ phương trnh
1
2
mx y
x my
+=
+=
với
m
là tham số thc. Có bao nhiêu giá tr của tham số
m
để hệ đ cho
vô nghiệm ?
A.
2.
B.
1.
C.
3.
D.
4.
Câu 31: Cho hai phương trnh :
4mx y m− = − −
(1) và
2 ( 1)x m y m− + = −
( 2) , với
m
là tham số thc.
Có bao nhiêu giá tr nguyên của tham số
m
thuộc đoạn
2;2021−
để hai phương trnh đ cho c nghiệm chung ?
A.
2021.
B.
2022.
C.
2023.
D.
2024.
Câu 32: Xét hệ phương trnh
22
2 2 4
a x y a
x a y a
+ = +
+ = +
với
a
là tham số thc. Có bao nhiêu giá tr nguyên dương nh
hơn 20 của tham số
a
để hệ đ cho c đng 4 nghiệm phân biệt?
A.
18.
B.
17.
C.
15.
D.
19.
Câu 33: Tổng của cc vectơ
AB CD AC DA BC+ + + +
là
A.
0
.
B.
AC
.
C.
DC
.
D.
AD
.
Câu 34. Cho hình thoi
ABCD
cạnh
a
và có
0
120BAD =
. Tính
AB DA−
?
A.
| | 2AB DA a−=
.
B.
| | 0AB DA−=
.
C.
| | 2AB DA a−=
.
D.
||AB DA a−=
.
Câu 35 . Cho tam giác
ABC
có
G
là trng tâm. Gi
I
l trung điểm cạnh
BC
. Mệnh đề no sau đây sai?
A.
3MA MB MC MG+ + =
, với mi điểm
M
.
B.
0GA GB GC+ + =
.
C.
2GB GC GA+=
.
D.
2AB AC AI+=
.
Câu 36 . Trong mt phẳng ta độ
Oxy
cho tam giác
ABC
có
(1;2), (3;4), ( 1;8)A B C −
. Gi
,MN
ln lưt là trung
điểm các cạnh
,AB AC
. Tìm ta độ vectơ
MN
?
A.
(1;6)MN =
.
B.
(2; 2)MN =−
.
C.
( 2;2)MN =−
.
D.
( 4;4)MN =−
.
Câu 37. Trong mt phẳng ta độ
Oxy
, cho tam giác
ABC
có
(1;2), (3;4), ( 1;3)A B C −
. Gi
G
l trng tâm tam
giác
ABC
. Điểm
D
tha mn
2 2 0GD DA DB+ − =
. Ta độ điểm
D
là:
A.
(1;3)
. B.
(5;7)
C.
( 3;-1)−
. D.
( )
5; 7−−
.
Câu 38. Cho hình vuông
ABCD
. Tính
( )
,AB CA
?
A.
0
45
. B.
0
90
. C.
0
135
. D.
0
150
.
Câu 39. Cho
tha mãn
00
90 180

. Chn mệnh đề đng trong các mệnh đề sau:
A.
cos 0
. B.
tan 0
. C.
cot 0
. D.
sin 0
.
Câu 40. Cho
3
sin ,90 180
5
xx

=
. Giá tr của biểu thức
2
P tan cosxx=
bằng
A.
12
25
. B.
25
12
. C.
25
12
−
. D.
12
25
−
.
Câu 41. Trong hệ ta độ
( )
;,O i j
, cho hai vc tơ
46a i j=+
và
37b i j=−
. Tính
.ab
?
A.
. 6.ab=
B.
. 30.ab=−
C.
. 30.ab=
D.
. 54.ab=
Câu 42. Cho
M
l trung điểm đoạn thẳng
AB
, đẳng thức nào sai?
А.
..MA AB MA AB=−
B.
..MA MB MA MB=
C.
..AM AB AM AB=
D.
..AM MB AM MB=
Câu 43. Cho hình ch nhật
ABCD
có
2,AB a AD a==
. Gi
M
l trung điểm cạnh
AB
. Tính
.CM BD
?
A.
2
2
a
−
. B.
2
3a
. C.
2
a
. D.
2
a−
.
Câu 44. Trong mt phẳng ta độ
Oxy
, cho tam giác
ABC
có
(2; 1), (1;2), (3;4)A B C−
. Gi
( ; )H x y
l chân đường
cao
AH
của tam giác
ABC
. Tổng
2
3S x xy=+
bằng
A.
2
. B.
1
. C.
7
. D.
0
.
Câu 45. Trong mt phẳng ta độ
Oxy
, cho tam giác
ABC
vuông cân tại
C
. Biết điểm
( 2;4), (6; 4)AB−−
v điểm
C nằm phía trên trục honh .Tnh độ di đoạn thẳng CO?
A.
2 13
. B.
53
. C.
25
. D.
52
.
Câu 46. Tìm tất c các giá tr thc của tham số
m
để phương trnh
2
21x m x+ = +
c
2
nghiệm phân biệt
1
x
,
2
x
.
A.
22m−
. B.
22m−
. C.
2m −
hoc
0m
. D.
2m −
.
Câu 47. Cho tam giác
ABC
đều cạnh
a
và
k
là một số thc âm thay đổi. Tập hp cc điểm
M
tha mãn
3(1 )k MA MB kMC O− + − =
là
A. Một đường tròn có bán kính bằng
a
.
B. Một đoạn thẳng c độ dài bằng
2
a
.
C. Một đoạn thẳng c độ dài bằng
4
a
.
D. Một đoạn thẳng c độ dài bằng
a
.
Câu 48. Cho tam giác
ABC
đều cạnh
a
. Gi
M
là một điểm bất kì . Tổng
2 2 2
2S MA MB MC= + −
đạt giá tr nh
nhất bằng?
A.
2
a
. B.
2
2
a
−
. C.
2
2a
. D.
2
3
2
a−
.
Câu 49. Gi
x a b c=+
(với
, , ; 0a b c b
) là một nghiệm của của phương trnh
22
(2 1) 2 3 4 7.− − = − − +x x x x
Tính
abc++
.
A. 0. B. 1. C. 2. D. 3.
Câu 50. Có bao nhiêu giá tr nguyên của
m
để phương trnh
( )
4 3 2 2
3
2 8 8 2 2 4 1 2 0
2
x x x m x x m++
− + −

+

=−
có
đng
3
nghiệm thuộc
2;1−
.
A.
1
. B.
2
. C.
3
. D.
0
.
_______________ HẾT _______________
MA TRN KIM TRA TRC NGHIM KHCH QUAN (50 câu - 10đim)
TT
Nội dung/bài/chủ đề
Mức độ
Số câu
Ghi chú
Nhận
biết
Thông
hiểu
Vận
dụng
Vận
dụng
cao
1
Mệnh đề, tập hp
2
3
5
1,0 điểm
2
Đại cương về hàm số.
2
2
1
5
1,0 điểm
3
Hàm số bậc nhất, bậc hai.
3
3
1
7
1,4 điểm
4
Phương trnh (điều kiện
xc đnh, php bđ tương
đương, pt hệ qu )
2
1
3
0,6 điểm
5
Pt bậc nhất, pt bậc hai v
pt quy về bậc 1, 2)
1
2
1
1
5
1,0 điểm
6
Đnh l vi-t v ứng dụng
1
2
1
1
5
1,0 điểm
7
Hệ phương trnh bậc nhất
nhiều n.
2
2
1
5
1,0 điểm
8
Tổng, hiệu của cc vectơ.
1
1
2
0,4 điểm
9
Tch của một vectơ với
một số.
1
1
2
0,4 điểm
10
Hệ trục ta độ
1
1
2
0,4 điểm
11
Ga tr lưng gic của gc
t 0
0
đến 180
0
; Gc gia
hai vecto.
2
1
3
0,6 điểm
12
Tch vô hướng của hai
vecto (Đnh ngha, tnh
chất, ứng dụng, biểu thức
ta độ)
2
2
1
1
6
1,2 điểm
Tổng số
0,2x20=
4,0 điểm
0,2x20=
4,0điểm
0,2x5=
1,0điểm
0,2x5 =
1,0điểm
50
10điểm
| 1/8
| | Tải xuống

Có thể bạn quan tâm:

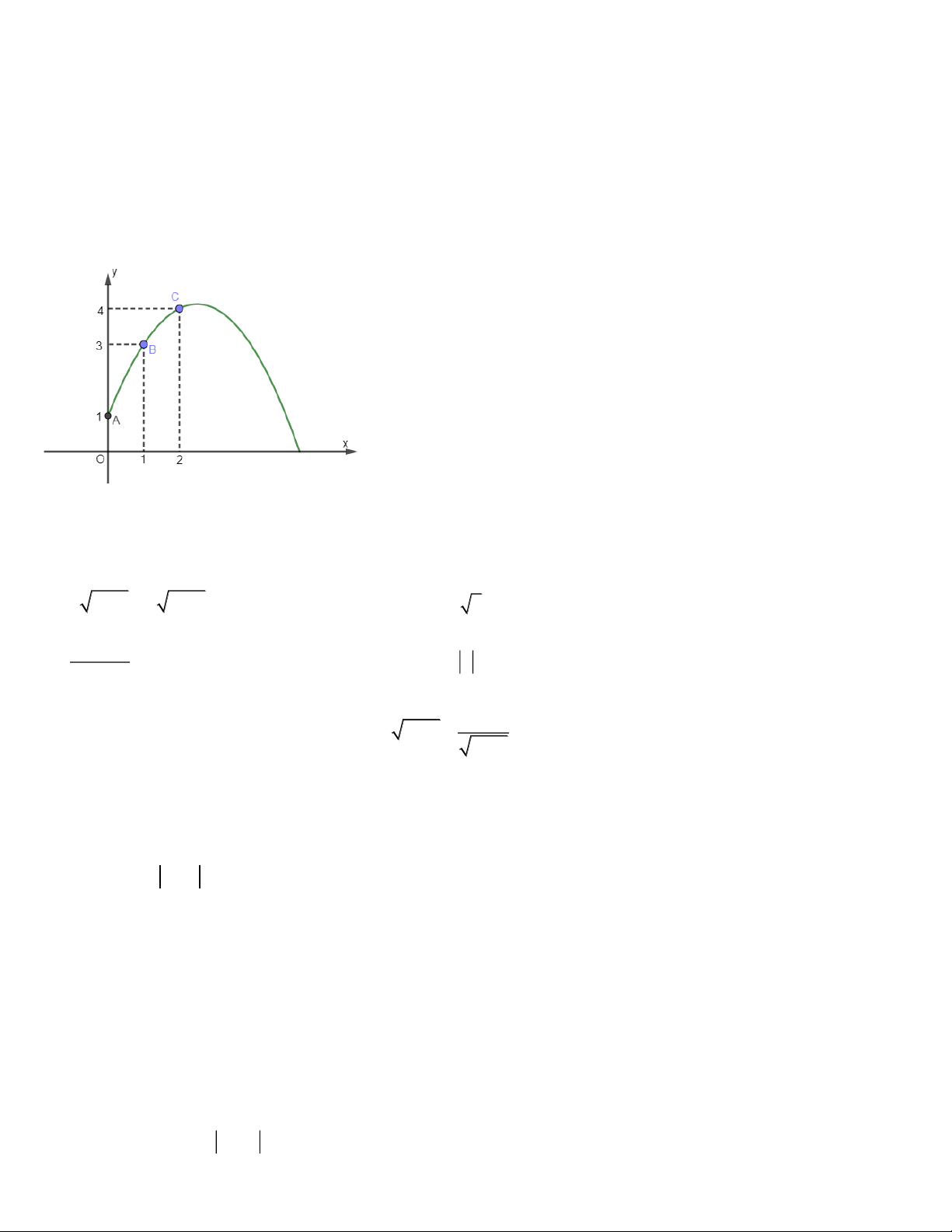
Preview text:

TRƯỜNG THPT
KIỂM TRA HỌC KÌ 1 NĂM HỌC 2021 – 2022 NGUYỄN GIA THIỀU
MÔN TOÁN – LỚP 10 ĐỀ CHÍNH THỨC
Thời gian làm bài: 90 phút (không kể thời gian giao đề
Họ và tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Câu 1. Cho tập hợp A và a là một phần tử của tập hợp A. Trong các mệnh đề sau, mệnh đề nào sai?
A. {a}  A .
B. {a}  A .
C. a A . D.   A.
Câu 2. Cho mệnh đề chứa biến P(n) : “ 2
n −1 chia hết cho 4 ” với n là số nguyên. Chọn mệnh đề đúng trong các mệnh đề sau: A. P(5) . B. P(2) . C. P(4) . D. P(6) .
Câu 3. Mệnh đề phủ định của mệnh đề “Phương trình 2
ax + bx + c = 0 (a  0) vô nghiệm” là: A. Phương trình 2
ax + bx + c = 0 (a  0) không có nghiệm. B. Phương trình 2
ax + bx + c = 0 (a  0) có nghiệm. C. Phương trình 2
ax + bx + c = 0 (a  0) có 2 nghiệm phân biệt. D. Phương trình 2
ax + bx + c = 0 (a  0) có nghiệm kép.
Câu 4. Gọi A là tập hợp các số thực không nhỏ hơn 1 và B là tập hợp các số thực có giá trị tuyệt đối nhỏ hơn 2. Tìm A B
A. A B = (1; 2) . B. A B  = [1;2) . C. A B  = [1;2]. D. A B  = ( 2 − ;1) .
Câu 5. Cho A = 0;1;2;3;  4 , B = 2;3;4;5; 
6 . Tập hợp ( A \ B) (B \ A)bằng? A. 5;  6 . B. 2;3;  4 . C. 1;  2 . D. 0;1;5;  6 .
Câu 6. Hàm số nào sau đây đồng biến trên khoảng (0;+ ) . A. 2 =
y = x − 2x + 2021. B. y x . C. 2
y = −x . D. y = 2 − x −1.
Câu 7. Hàm số nào trong các hàm số sau có đồ thị nhận Oy là trục đối xứng: 1 A. 2
y =1−3x + x .
B. y = x −1 + x +1 . C. y = . D. 3 y = x . x  1  khi x  0 
Câu 8. Cho hàm số y =  x − 2 
. Tập xác định của hàm số là:
x + 2 khi x  0  A.
. B. x sao chox  −2}. C.  2; − +). D. \ {2}.
Câu 9. Trong các quy tắc sau, quy tắc nào không phải là một hàm số?
A. Quy tắc đặt tương ứng mỗi số thực dương với căn bậc hai của nó.
B. Quy tắc đặt tương ứng mỗi số thực với căn bậc ba của nó.
C. Quy tắc đặt tương ứng mỗi số thực với bình phương của nó.
D. Quy tắc đặt tương ứng mỗi số thực dương với giá trị tuyệt đối của nó. a
Câu 10. Biết giá trị nhỏ nhất của hàm số y = 3x −1 + x +1 là với * ( , a b N ;( , a )
b =1) . Tính a + b . b A. 3 B. 5 C. 2 D. 7
Câu 11. Tìm m để đường thẳng y = 3x +1 song song với đường thẳng y = ( 2 m − ) 1 x + (m − ) 1 . A. m = 2 − .
B. m = 0 . C. m = 2  . D. m = 2 .
Câu 12. Cho parabol (P) 2
: y = ax + bx + c (a  0) . Xét dấu hệ số a và biệt thức  khi ( P) cắt trục hoành tại 2
điểm phân biệt và có đỉnh nằm phía trên trục hoành.
A. a  0,   0.
B. a  0,   0.
C. a  0,   0.
D. a  0,   0. 1 9
Câu 13. Tìm tọa độ giao điểm hai parabol 2 y = x − 2x và 2 y = −2x + là: 2 2  5   9 9 − 9   −  A. 1 − ;   , ;   . B. (− ) 3 4;16 , 1;   .  2   5 50   2   3 −  C. 1;   . D. (2; 2 − ),( 2 − ;6).  2 
Câu 14. Giá trị nhỏ nhất của hàm số 2
y = 2x + x − 3 là: −21 −25 A. 2 − . B. . C. . D. 3 − . 8 8
Câu 15. Cho hàm số y = x + x +1 . Chọn mệnh đề sai trong các mệnh đề sau:
A. Hàm số có tập xác định là .
B. Hàm số đã cho là hàm số lẻ.
B. Hàm số đồng biến trên  1 − ;+ )  C. (− ;  − )
Hàm số không đổi trên 1
Câu 16. Khi một quả bóng được đá lên, nó sẽ đạt đến độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả
bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oxy, trong đó x là thời gian (tính bằng giây) kể từ khi quả
bóng được đá lên; y là độ cao (tính bằng mét) của quả bóng. Giả thiết rằng quả bóng được đá từ độ cao 1,0m. Sau đó
1 giây, quả bóng đạt độ cao 3m và 2 giây sau khi đá lên, nó ở độ cao 4m (xem hình vẽ sau). Hỏi sau bao lâu thì quả
bóng sẽ đạt được độ cao lớn nhất kể từ khi đá lên (tính chính xác đến hàng phần trăm)? A. 2,51. B. 2,50 C. 2,52. D. 2,53 .
Câu 17. Chọn phép biến đổi đúng trong các phép biến đổi sau:
A. x 2 − x = 3 2 − x  x = 3 B. 2
x = x − 2  x = (x − 2) x(x − 2) C. = 2  x = 2  x = x −
D. x = 2 2 4 2 2 x + 5
Câu 18. Điều kiện xác định của phương trình x − 2 + = 0 là : 7 − x A. x  2 B. x  7
C. 7  x  2
D. 7  x  2
Câu 19. Xét lời giải bài toán sau khi giải phương trình: x −1 = x − 3 2 2
 (x −1) = (x − 3) (1) 2 2
x − 2x +1 = x − 6x + 9 (2)  x = 2 (3)
Thử lại ta thấy x = 2 không thỏa mãn phương trình đã cho. Vậy phương trình đã cho vô nghiệm.
Hỏi lời giải trên đúng hay sai. Nếu sai thì sai ở bước nào?
A. Lời giải đúng.
B. Sai ở bước 2 C. Sai ở bước 3 D. Sai ở bước 1
Câu 20. Phương trình 3x −1 − 3x +1 = 0 có bao nhiêu nghiệm? A. 0 B. 1 C. 2 D. Vô số.
Câu 21. Có bao nhiêu giá trị nguyên của tham số m thuộc 5;4 để phương trình 2 2 m 4 x 5 m 2m 0 có nghiệm. A. 2 . B. 9 . C. 10 . D. 11.
Câu 22. Phương trình 4 2 2 3
− x +(2m−1)x + 2.m +1= 0 (với m là tham số) có bao nhiêu nghiệm ?
A. Có 2 nghiệm. B. Có 3 nghiệm. C. Có 4 nghiệm. D. Vô nghiệm.
Câu 23. Phương trình 2 ax bx c 0 a
0 có hai nghiệm cùng dấu khi và chỉ khi :   0   0   0   0 A.  . B.  . C.  . D.  . P  0 P  0 S  0 S  0
Câu 24. Giả sử phương trình 2 2 x 2m 1 x m m
0 ( m là tham số) có hai nghiệm là x ; x . Tính giá trị biểu 1 2 thức P x
x theo m . 1 2
A. P = 2m . B. P = 2m + 2 .
C. P = 1. D. P = 1  2
Câu 25. Tìm m để phương trình 2x − 4x − 5 = m có 2 nghiệm phân biệt.
A. 0  m  7 . B. m  7 . C. m(7;+) {0}. D. m  ( 7 − ;+) .
Câu 26. Cho parabol (P) 2
: y = x − 2x −10 và đường thẳng d : y = mx −10 . Tìm tổng tất cả các giá trị của tham số
m để d cắt ( P) tại hai điểm phân biệt ,
A K sao cho diện tích tam giác OAK bằng 5 . A. 2 − . B. 4 − . C. 1 − . D. 3 − . 2 − +
Câu 27. Tổng các nghiệm của phương trình x
4x 2 = x − 2 là: A. 4 B. 3 C. 5 D. 2 x − 2
Câu 28: Trong mặt phẳng tọa độ Oxy , giao điểm của hai đường thẳng (d ) : 2x + y = 1
− và (d ') : 6x + 3y = 3 − là A. M (3; 1 − ). B. N (1; 3 − ). C. P( 1 − ;3). D. Q( 3 − ;1).
Câu 29: Trong các hệ phương trình sau, hệ phương trình nào vô số nghiệm? x + 7y =16 4x −3y = 5 x − 3y = 5 − 6x − 3y = 1 − A. . B. . C. . D. . 7  x + y = 1 − 6 3  x + 4y = 3  2 − x + 6y =10  8 − x + 4y = 1 − mx + y =1
Câu 30: Xét hệ phương trình 
với m là tham số thực. Có bao nhiêu giá trị của tham số m để hệ đã cho x + my = 2 vô nghiệm ? A. 2. B. 1. C. 3. D. 4.
Câu 31: Cho hai phương trình : mx − y = 4
− − m (1) và 2x − (m +1)y = −m ( 2) , với m là tham số thực.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn  2 − ;202 
1 để hai phương trình đã cho có nghiệm chung ? A. 2021. B. 2022. C. 2023. D. 2024.
a x + 2 y = a + 2 
Câu 32: Xét hệ phương trình 
với a là tham số thực. Có bao nhiêu giá trị nguyên dương nhỏ
2 x + a y = 2a + 4 
hơn 20 của tham số a để hệ đã cho có đúng 4 nghiệm phân biệt? A. 18. B. 17. C. 15. D. 19.
Câu 33: Tổng của các vectơ AB + CD + AC + DA + BC là A. 0 . B. AC . C. DC . D. AD . 0
Câu 34. Cho hình thoi ABCD cạnh a và có BAD =120 . Tính AB − DA ?
A. | AB − DA |= 2a .
B. | AB − DA |= 0 .
C. | AB − DA |= a 2 .
D. | AB − DA |= a .
Câu 35 . Cho tam giác ABC có G là trọng tâm. Gọi I là trung điểm cạnh BC . Mệnh đề nào sau đây sai?
A. MA + MB + MC = 3MG , với mọi điểm M .
B. GA + GB + GC = 0 .
C. GB + GC = 2GA .
D. AB + AC = 2AI .
Câu 36 . Trong mặt phẳng tọa độ Oxy cho tam giác ABC có (
A 1; 2), B(3; 4), C( 1
− ;8) . Gọi M , N lần lượt là trung điểm các cạnh A ,
B AC . Tìm tọa độ vectơ MN ?
A. MN = (1;6) . B. MN = (2; 2 − ). C. MN = ( 2 − ;2). D. MN = ( 4 − ;4).
Câu 37. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có (
A 1; 2), B(3; 4), C( 1
− ;3) . Gọi G là trọng tâm tam
giác ABC . Điểm D thỏa mãn GD + 2DA − 2DB = 0 . Tọa độ điểm D là: A. (1;3) . B. (5; 7) C. ( 3 − ;-1) . D. ( 5 − ; 7 − ).
Câu 38. Cho hình vuông ABCD . Tính ( AB,CA) ? A. 0 45 . B. 0 90 . C. 0 135 . D. 0 150 .
Câu 39. Cho  thỏa mãn 0 0
90    180 . Chọn mệnh đề đúng trong các mệnh đề sau:
A. cos  0 .
B. tan  0.
C. cot  0 .
D. sin  0 . 3
Câu 40. Cho sin x , 90 x 180 =  
. Giá trị của biểu thức 2
P = tan x  cos x bằng 5 12 25 25 12 A. . B. . C. − . D. − . 25 12 12 25
Câu 41. Trong hệ tọa độ ( ;
O i, j ), cho hai véc tơ a = 4i + 6 j và b = 3i − 7 j . Tính . a b ? A. . a b = 6. B. . a b = 3 − 0. C. . a b = 30. D. . a b = 54.
Câu 42. Cho M là trung điểm đoạn thẳng AB , đẳng thức nào sai? А. M . A AB = −M . A AB B. M . A MB = M .
A MB C. AM .AB = AM .AB
D. AM .MB = AM .MB
Câu 43. Cho hình chữ nhật ABCD có AB = 2a, AD = a . Gọi M là trung điểm cạnh AB . Tính CM .BD ? 2 a A. − . B. 2 3a . C. 2 a . D. 2 −a . 2
Câu 44. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có ( A 2; 1
− ), B(1;2),C(3;4) . Gọi H ( ;
x y) là chân đường 2
cao AH của tam giác ABC . Tổng S = x + 3xy bằng A. 2 . B.1. C. 7 . D. 0 .
Câu 45. Trong mặt phẳng tọa độ Oxy , cho tam giác ABC vuông cân tại C . Biết điểm ( A 2 − ;4), B(6; 4 − ) và điểm
C nằm phía trên trục hoành .Tính độ dài đoạn thẳng CO? A. 2 13 . B. 53 . C. 2 5 . D. 5 2 .
Câu 46. Tìm tất cả các giá trị thực của tham số m để phương trình 2
2x + m = x +1 có 2 nghiệm phân biệt x , x . 1 2 A. 2
−  m  2 . B. 2
−  m  2 . C. m  2
− hoặc m  0. D. m  2 − .
Câu 47. Cho tam giác ABC đều cạnh a và k là một số thực âm thay đổi. Tập hợp các điểm M thỏa mãn
3(1− k)MA+ MB − kMC = O là
A. Một đường tròn có bán kính bằng a . a
B. Một đoạn thẳng có độ dài bằng . 2 a
C. Một đoạn thẳng có độ dài bằng . 4
D. Một đoạn thẳng có độ dài bằng a .
Câu 48. Cho tam giác ABC đều cạnh a . Gọi M là một điểm bất kì . Tổng 2 2 2
S = MA + 2MB − MC đạt giá trị nhỏ nhất bằng? 2 a 2 3 − a A. 2 a . B. − . C. 2 2a . D. . 2 2
Câu 49. Gọi x = a b + c (với , a ,
b c  ; b  0 ) là một nghiệm của của phương trình 2 2
(2x −1) 2x − 3 = 4
− x − x + 7.
Tính a + b + c . A. 0. B. 1. C. 2. D. 3.  3 
Câu 50. Có bao nhiêu giá trị nguyên của m để phương trình 4 3 2
2x + 8x + 8x − 2m −  ( 2
2x + 4x) +1− 2m = 0 có  2 
đúng 3 nghiệm thuộc  2 − ;  1 . A. 1. B. 2 . C. 3 . D. 0 .
_______________ HẾT _______________
MA TRẬN KIỂM TRA TRẮC NGHIỆM KHÁCH QUAN (50 câu - 10điểm) Mức độ TT Nội dung/bài/chủ đề Vận Số câu Ghi chú Nhận Thông Vận dụng biết hiểu dụng cao 1 Mệnh đề, tập hợp 2 3 5 1,0 điểm 2
Đại cương về hàm số. 2 2 1 5 1,0 điểm 3
Hàm số bậc nhất, bậc hai. 3 3 1 7 1,4 điểm
Phương trình (điều kiện 4
xác định, phép bđ tương 2 1 3 0,6 điểm đương, pt hệ quả )
Pt bậc nhất, pt bậc hai và 5 1 2 1 1 5 1,0 điểm pt quy về bậc 1, 2) 6
Định lý vi-ét và ứng dụng 1 2 1 1 5 1,0 điểm
Hệ phương trình bậc nhất 7 2 2 1 5 1,0 điểm nhiều ẩn. 8
Tổng, hiệu của các vectơ. 1 1 2 0,4 điểm
Tích của một vectơ với 9 1 1 2 0,4 điểm một số. 10 Hệ trục tọa độ 1 1 2 0,4 điểm
Gía trị lượng giác của góc 11
từ 00 đến 1800 ; Góc giữa 2 1 3 0,6 điểm hai vecto. Tích vô hướng của hai
vecto (Định nghĩa, tính 12 2 2 1 1 6 1,2 điểm
chất, ứng dụng, biểu thức tọa độ) 0,2x20= 0,2x20= 0,2x5= 0,2x5 = Tổng số 50 10điểm 4,0 điểm 4,0điểm 1,0điểm 1,0điểm