Đề thi học kì 1 Toán 12 năm 2019 – 2020 trường Long Thạnh – Kiên Giang

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra học kỳ 1 môn Giới Toán 12 năm học 2019 – 2020 .Mời bạn đọc đón xem.

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/6 - Mã đề 268
TRƯỜNG THPT LONG THẠNH
TỔ: TOÁN
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 – 2020
MÔN THI: TOÁN 12
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Ngày thi: 14/12/2019
(Đ
ề có
06
trang)
Câu 1: Đồ thị cho bên dưới là của một trong bốn hàm số dưới đây. Chọn khẳng định đúng
A. Hàm số bậc ba.
B. Hàm số bậc hai.
C. Hàm số bậc bốn. D. Hàm số phân thức hữu tỉ.
Câu 2: Cho hàm số
()yfx=
có bảng biến thiên như hình bên dưới
Giá trị cực đại của hàm số đã cho bằng
A. 9. B. 2. C. 13. D. 10- .
Câu 3: Khối lăng trụ có diện tích đáy B, chiều cao h thì thể tích bằng
A. Bh . B.
1
6
Bh
. C.
1
3
Bh
. D. 3Bh .
Câu 4: Khi xoay một tam giác vuông quanh một cạnh góc vuông, hình tròn xoay được tạo ra là :
A. Hình chóp. B. Hình trụ. C. Hình lăng trụ. D. Hình nón.
Câu 5: Hình đa diện như hình bên dưới có bao nhiêu cạnh ?
A. 6. B. 18. C. 12. D. 24.
Câu 6: Có bao nhiêu loại khối đa diện đều ?
A. Vô số. B. 4.
C. 5. D. 6.
Câu 7: Đồ thị bên phải là của một trong bốn hàm số được liệt kê dưới
đây. Chọn khẳng định đúng.
A.
1
3
log.yx=
B.
1
.
3
x
y
æö
=
ç÷
èø
C.
3
log.
yx=
D.
3.
x
y=
Mã đề 268
Trang 2/6 - Mã đề 268
Câu 8: Cho hàm số
2
23
yxx=-+. Giá trị nhỏ nhất của hàm số là
A. 0 . B.
2
. C.
1
. D. 3.
Câu 9: Giải bất phương trình
5124
x
>
ta được
A.
5
log124x >
. B.
5
log124x <
. C.
124
log5x>
. D.
124
log5x<
.
Câu 10: Phương trình
264
x
=
có nghiệm là
A. 6x =- . B. 32.x = C. 6.x = D. 5x = .
Câu 11: Cho hàm số
32
23
yxx=-- . Đồ thị hàm số cắt trục tung
Oy
tại điểm
M
có tọa độ là
A.
(0;3)M
. B.
(0;1).M -
C.
(0;3).M -
D.
(3;1)M
.
Câu 12: Công thức tính thể tích khối cầu có bán kính R là
A.
3
4VR
p
=
. B.
3
4
3
VR
p
=
. C.
2
4
3
VR
p
=
. D.
2
4VR
p
=
.
Câu 13: Với 01a<¹ và
,bc
là số thực dương. Chọn khẳng định sai.
A.
logloglog
aaa
b
bc
c
æö
-=
ç÷
èø
. B.
ln
log
ln
a
b
b
a
=
.
C.
logloglog()
aaa
bcbc+=+
. D.
log
log
log
a
c
c
a
=
.
Câu 14: Tìm tập xác định của hàm số
( )
3
7
yx
-
=-
.
A.
{}
\7
¡
. B.
( )
;7-¥ . C.
{ }
\7-
¡
. D.
( )
7; +¥ .
Câu 15: Khối chóp có diện tích đáy B, chiều cao h thì công thức tính thể tích V là
A. VBh= . B. 3VBh= . C.
1
VBh
=
. D.
1
6
VBh
=
.
Câu 16: Thu gọn biểu thức,
3
4
2
(0)
a
Aa
a
=>
, kết quả đúng là
A.
5
6
.a B.
5
6
.a
-
C.
1
4
.a D.
5
4
.a
-
Câu 17: Cho hàm số
2
1
x
y
x
+
=
-
. Đồ thị hàm số có tiệm cận đứng là
A.
1
2
x
=
. B.
1.x
=
C.
1x
=-
. D.
2.x
=
Câu 18: Cho hàm số
()yfx=
có bảng biến thiên như hình bên dưới.
Hỏi hàm số đã cho đồng biến trên khoảng nào ?
A.
( )
;20-¥- . B.
( )
11; +¥ . C.
( )
1982;2019- . D.
( )
20;11- .
Câu 19: Giải bất phương trình
( )
1
6
log43x-³-
. Ta được
A. 220x ³ . B. 220x > . C. 4220x<< . D. 4220x<£ .
Trang 3/6 - Mã đề 268
Câu 20: Một hình cầu có bán kính bằng
6cm
. Một mặt phẳng đi qua tâm của mặt cầu. Tính diện
tích S thiết diện của mặt cầu và mặt phẳng.
A.
2
18Scm
p
=
. B.
2
9Scm
p
=
. C.
2
144Scm
p
=
. D.
2
36Scm
p
=
.
Câu 21: Với a ,b,c là các số thực dương tùy ý và a khác 1. Đặt
2
84
Ploglog
a
a
bb=+
. Mệnh đề đúng là
A.
5log.
a
Pb
=
B.
7log.
a
Pb
=
C.
12log.
a
Pb
=
D.
8log.
a
Pb
=
Câu 22: Giải phương trình
2
2
log(7)4x+=
ta được tập nghiệm
A.
{}
3S= . B.
{ }
3S =- . C.
{ }
9;9S =- . D.
{ }
3;3S =- .
Câu 23: Cho hàm số
( )
5
2
()4fxxx=- ,
()fx
có đạo hàm là
A.
2
'()5(24)(4).
fxxxx
=-- B.
24
'()5(4).
fxxx
=-
C.
24
'()5(24)(4).
fxxxxx=-- D.
24
'()5(24)(4).
fxxxx=--
Câu 24: Cho hàm số
32
yaxbxcxd=+++ .Chọn khẳng định đúng:
A. Hàm số đồng biến trên
¡
khi
0'y
=
vô nghiệm hoặc nghiệm kép và a < 0.
B. Hàm số có một cực đại và một cực tiểu khi
0'y
=
có hai nghiệm phân biệt.
C. Hàm số không có cực trị khi
0'y
=
có nghiệm.
D. Hàm số nghịch biến trên
¡
khi
0'y
=
vô nghiệm hoặc nghiệm kép và a >0.
Câu 25: Hộp nước sơn hình trụ có kích thước như hình vẽ. Tính thể tích V của hộp nước sơn đó.
A.
3
24000Vcm=
. B.
3
96000Vcm=
. C.
3
96000Vcm
p
=
. D.
3
24000Vcm
p
=
.
Câu 26: Trong các hàm số sau, hàm số nào là hàm số mũ ?
A.
1
3
x
y =
. B.
yx=
. C.
2
yx
-
=
. D.
1
3
yx=
.
Câu 27: Viết dạng lũy thừa với số mũ hữu tỉ của biểu thức
2
3
.aa
(
0
a >
). Kết quả đúng là
A.
6
7
.a B.
1
6
.a C.
7
6
.a D.
7
3
.a
Câu 28: Trong bốn hình dưới đây, có bao nhiêu hình là khối đa diện ?
A. 3. B. 1. C. 4. D. 2.
Trang 4/6 - Mã đề 268
Câu 29: Khối chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, SA = là đường cao. Thể
tích V của khối chóp là
A.
3
2
.
2
a
V = B.
3
2
.
3
a
V = C.
3
2.Va
=
D.
3
2
.
6
a
V =
Câu 30: Trong các hàm số sau, hàm số nào đồng biến trên tập
¡
.
A.
3
32
yxx=-++. B.
3
3
yxx=+. C.
3
32
yxx=--+. D.
3
3
yxx=-+ .
Câu 31: Cho hàm số
()yfx=
liên tục trên đoạn
[ ]
16;13-
và có đồ thị như hình bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên đoạn
[ ]
16;13-
. Tính
Mm
+
ta được.
A.
5
-
. B.
2
-
. C.
4
-
. D.
11
-
.
Câu 32: Phương trình 165.440
xx
-+=
có hai nghiệm
,ab
, tổng ab+ bằng :
A. 1. B. 0. C. 5.
D. 4.
Câu 33: Cho hàm số
2
sin
()5
x
fx= . Đạo hàm của hàm số
()fx
là
A.
2
sin
5.ln5.sin2.
x
x B.
2
sin
5.ln5.
x
C.
2
sin
5.ln5.2sin.
x
x D.
2
sin
5.ln5.2cos.
x
x
Câu 34: Biết khối đa diện đều loại
{3;4}
có độ dài cạnh bằng
123cm
. Tính diện tích toàn phần của
khối đa diện đều đó.
A.
2
2592cm
. B.
2
1728cm
. C.
2
8643
cm
. D.
2
6483
cm
.
Câu 35: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh BB’ = a và tạo với
đáy một góc bằng 60
0
. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC.
Thể tích khối lăng trụ ABC.A’B’C’ là
A. . B. . C. . D. .
Câu 36: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
3
499
x
y
xx
+
=
--+
là
A. 1. B. 2. C. 3. D. 4.
Câu 37: Giá trị của
m
để đồ thị hàm số
42
83fxxx() cắt đường thẳng
3ym
tại 4 điểm phân
biệt khi
A. 939.m<< B.
13
m1.
3
-<<
C. 313m<<. D. 133.m-<<
Câu 38: Cho hàm số
42
(1)21
yxmxm=-+++ có đồ thị
()
m
C
đi qua điểm
(1,3)M
Giá trị của
m
là
A. 1m = . B. 2m =- . C. 2m = . D. 0.m =
2
a
3
33
80
a
3
93
80
a
3
3
80
a
3
9
80
a
Trang 5/6 - Mã đề 268
Câu 39: Cho hình chóp tam giác .SABCD có đáy là hình vuông cạnh 6a . Tam giác SAB đều và
nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp
.SABCD theo a.
A.
3
2621Va
p
=
. B.
3
2821Va
p
=
. C.
3
3021Va
p
=
. D.
3
2421Va
p
=
.
Câu 40: Tìm tập xác định D của hàm số
22
loglog(4)
yxx=++
.
A.
)
26;D
é
=-++¥
ë
. B.
( )
25;D =-++¥ . C.
( )
26;D =-++¥ . D.
)
25;D
é
=-++¥
ë
.
Câu 41: Hàm số
23
(2019)(2020)
yxx=+- có bao nhiêu điểm cực trị ?
A. 4. B. 3. C. 2. D. 1.
Câu 42: Tìm tất cả giá trị thực của m để hàm số
sin2019
x
yx
m
=-+
nghịch biến trên toàn trục số.
A.
0m
>
. B.
1m
³
hoặc
0m
<
. C.
1m £
. D.
01m<£
.
Câu 43: Tìm tất cả cá giá trị của
m
để phương trình
2
2
2
log8log840
xxm--+=
vô nghiệm trên
đoạn
[ ]
1;4
.
A. 0m < hoặc
1
2
m
>
. B.
1
0
2
m
<<
C. 0m < . D. 0m £ hoặc
1
2
m
³
.
Câu 44: Hình vẽ bên là đồ thị của hàm số
()
.yfx=
Gọi S là tập hợp các số nguyên dương của tham
số m để hàm số
( )
1yfxm=-+
có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
A. 9. B. 18. C. 15. D. 12.
Câu 45: Cho hình chóp tứ giác .SABCD có đáy là hình vuông cạnh 2a . Biết hình chiếu vuông góc
của đỉnh S lên mặt phẳng đáy là điểm M trung điểm cạnh AD và tam giác SMB cân. Tính thể tích V
của khối chóp .SMBCD .
A.
3
5Va= . B.
3
45
3
a
V=
. C.
3
3Va= . D.
3
5
3
a
V =
.
Câu 46: Bác nông dân T bán lúa và một đàn lợn thu được 120 triệu đồng. Bác T dự định gửi tiết
kiệm toàn bộ số tiền này vào ngân hàng với lãi suất
0,9%/
tháng. Hỏi sau hai năm mới rút toàn bộ
tiền gốc và tiền lãi cho con đi học, khi đó bác T thu được bao nhiêu ? (giả sử lãi suất không đổi và
kết quả làm tròn đến 3 chữ số thập phân theo đơn vị triệu đồng)
A.
148,788
triệu đồng. B.
122,169
triệu đồng.
C.
148,789
triệu đồng. D.
122,170
triệu đồng.
Trang 6/6 - Mã đề 268
Câu 47: Một trang trại trồng rau sạch theo tiêu chuẩn VietGap tại địa điểm B để cung cấp cho siêu
thị A đặt trên hòn đảo cách xa đất liền 160km (đoạn AH trên hình vẽ). Người ta dự định xây một
trạm tàu tại vị trí C để vận chuyển rau xanh ra đảo. Biết rằng tốc độ vận chuyển của xe chở trên đất
liền là 70km/h và của tàu hàng trên biển là 40km/h. Hỏi phải chọn điểm C cách B bao xa để thời
gian vận chuyển rau xanh ra đảo là ít nhất, biết khoảng cách từ trang trại B đến siêu thị A trên đảo là
300km. (kết quả làm tròn đến 2 chữ số thập phân)
A. 142,36 km. B. 142,34 km. C. 142,40 km. D. 142,38 km.
Câu 48: Một hình nón có góc ở đỉnh bằng
0
60 và đường kính đường tròn đáy bằng 8a . Mặt phẳng
()
a
đi qua đỉnh của hình nón và cách tâm đường tròn đáy 2a . Tính diện tích S thiết diện của mặt
phẳng
()
a
cắt hình nón đã cho.
A.
2
482
11
a
S =
. B.
2
1922
11
a
S =
. C.
2
3842
11
a
S =
. D.
2
962
11
a
S =
.
Câu 49: Có bao nhiêu giá trị nguyên của tham số
[ ]
2019;2019a Î- để hàm số
4223
2yxaxaa=--+
tiếp xúc với trục hoành tại hai điểm phân biệt.
A. 2020. B. 3. C. 2. D. 1.
Câu 50: Cho hàm số

yfx
có bảng biên thiên như hình vẽ
Hàm số
()
2
53
2
22
gxfxx
æö
=--
ç÷
èø
nghịch biến trên khoảng
A.
5
1;.
4
æö
ç÷
èø
B.
1
1;.
4
æö
-
ç÷
èø
C.
9
;.
4
æö
+¥
ç÷
èø
D.
1
;1.
4
æö
ç÷
èø
----------- HẾT ----------
Học sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm
Họ và tên học sinh:................................................................. Số báo danh:............................
Trang 1/6 - Mã đề 182
TRƯỜNG THPT LONG THẠNH
TỔ: TOÁN
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 – 2020
MÔN THI: TOÁN 12
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Ngày thi: 14/12/2019
(Đ
ề có
06
trang)
Câu 1: Cho hàm số
()yfx=
có bảng biến sau, chọn khẳng định đúng.
A. Hàm số nghịch biến trên khoảng
(2;)+¥
. B. Hàm số nghịch biến trên khoảng
(0;2)
.
C. Hàm số đồng biến trên khoảng
(0;2)
. D. Hàm số đồng biến trên khoảng
(;2)-¥
.
Câu 2: Tìm tập xác định D của hàm số
( )
3,14
log5yx=-.
A.
( )
;5D =-¥ . B.
(
]
;5D =-¥ . C.
[
)
5;D =+¥ . D.
( )
5;D =+¥ .
Câu 3: Giải phương trình
102019
x
=
ta được nghiệm
A.
log2019x =
. B.
10
2019x = . C.
2019
10
x
=
. D.
ln2019
x = .
Câu 4: Trong những công thức dưới đây, công thức sai là:
A. log1,(0,1).
a
aaa
=>¹
B. log1,(0,1).
a
aaa
=>¹
C. log10,(0,1).
a
aa
=>¹
D. log,(0,1).
a
aaa
a
a
=>¹
Câu 5: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất:
A. Bốn mặt. B. Hai mặt. C. Ba mặt. D. Năm mặt.
Câu 6: Công thức tính thể tích khối lăng trụ có diện tích đáy là B và chiều cao h là :
A. VBh= . B.
1
.
3
VBh=
C.
1
.
2
VBh=
D.
1
.
6
VBh=
Câu 7: Cho hàm số
()yfx=
có đồ thị như hình bên dưới.
Hỏi đường thẳng
2y =
cắt đồ thị hàm số đã cho tại bao nhiêu điểm ?
A. 1. B. 2. C. 4. D. 3.
Câu 8: Công thức tính diện tích xung quanh của hình nón có bán kính đáy r và đường sinh l là
A.
2
xq
Srl
p
=
. B.
2
22
xq
Srlr
pp
=+. C.
2
xq
Srlr
pp
=+. D.
xq
Srl
p
=
.
Câu 9: Đường tiệm cận đứng của đồ thị hàm số
5
4
x
y
x
+
=
-
là
A.
4
x =- . B.
4
x = . C.
5
x =- . D.
5
x = .
Mã đề 182
Trang 2/6 - Mã đề 182
Câu 10: Tìm giá trị lớn nhất của hàm số
8
()1
fx
x
=+
trên đoạn
[ ]
4;2019
.
A.
[ ]
4;2019
1
max()
2
fx
=-
. B.
[ ]
4;2019
max()5
fx=
. C.
[ ]
4;2019
2027
max()
2019
fx
=
. D.
[ ]
4;2019
max()3
fx=
.
Câu 11: Cho hàm số
()yfx=
có đồ thị như hình bên.
Số cực trị của hàm số là:
A.
1
. B.
3
. C.
0
. D.
2
.
Câu 12: Hình bát diện đều là khối đa diện đều loại
A.
{ }
4;3 . B.
{ }
5;3
. C.
{ }
3;4 . D.
{ }
3;3
.
Câu 13: Mặt cầu có bán kính là
R
thì có diện tích là :
A.
2
4.
SR
p
=
B.
2
.
SR
p
=
C.
3
4.
SR
p
=
D.
2
2.
SR
p
=
Câu 14: Công thức tính thể tích khối chóp có diện tích đáy là B và chiều cao h là :
A.
1
V.
2
Bh
=
B.
1
V.
3
Bh
=
C.
V.
Bh= D.
1
V.
6
Bh
=
Câu 15: Đồ thị bên dưới là của một trong bốn hàm số
()yfx=
được liệt kê ở bốn phương án. Hãy
chọn khẳng định đúng.
A.
32
243yxx=---
. B.
32
243yxx=-+
. C.
32
243yxx=--+
. D.
32
243yxx=--
.
Câu 16: Bất phương trình ,(0)
x
abb
>>
có nghiệm là :
A. log
a
xb
>
với
.a Î ¡
B. log
a
xb
<
với
1.
a >
C. log
a
xb
>
với
1.
a >
D. log
a
xb
>
với
01.
a<<
Câu 17: Cho hàm số yx
a
=
. Khẳng định sai là:
A. Tập xác định của hàm số là D = ¡ khi
a
Î ¡
.
B. Tập xác định của hàm số là D = ¡ khi
a
là số nguyên dương.
C. Tập xác định của hàm số là
{}
\0
D=¡
khi
a
là số nguyên âm.
D. Tập xác định của hàm số là
(0;)D=+¥
khi
a
Τ
Câu 18: Với
a
là số thực dương và ,
ab
Ρ. Chọn khẳng định sai.
A. .aaa
abab
+
= . B.
( )
.
aa
b
aab
=
. C.
a
a
a
a
ab
b
-
=
. D.
.
.aaa
abab
= .
x
y
-1
- 1
O
1
Trang 3/6 - Mã đề 182
Câu 19: Bất phương trình
3
log(1)2
x
+>
có nghiệm là:
A.
10
x
>
B.
5.
x
>
C.
8.
x
>
D.
8.
x
<
Câu 20: Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Về phía ngoài khối chóp
này ta ghép thêm một khối tứ diện đều có cạnh bằng a, sao cho một mặt của khối tứ diện đều trùng
với một mặt bên của khối chóp đã cho. Số mặt của khối đa diện mới lập thành là
A. 5. B. 8. C. 7. D. 6.
Câu 21: Hàm số
4
2020
yx
=-
nghịch biến trên khoảng nào ?
A.
(
)
2020;
-+¥
. B.
(
)
;2020
-¥ . C.
(
)
;0
-¥ . D.
(
)
0;
+¥
.
Câu 22: Thu gọn
3
32
4
..
ppp
ta được
A.
23
12
p
. B.
32
12
p
. C.
12
23
p
. D.
32
21
p
.
Câu 23: Mặt cầu ngoại tiếp một hình lập phương cạnh
a
thì có thể tích là:
A.
3
33
.
4
a
V
p
=
B.
3
27
.
4
a
V
p
=
C.
3
3
.
2
a
V
p
=
D.
3
3
.
6
a
V
p
=
Câu 24: Tìm điều kiện của
x
để hàm số
3
log(2)
yx
=-
xác định.
A.
2.
x
<
B.
2.
x
¹
C.
.
x
Î
¡
D.
2.
x
>
Câu 25: Tính đạo hàm của hàm số
( )
5
2
23
yx=- .
A.
( )
2
3
'523
yx=- . B.
( )
3
2
5
'23
2
yx=-
. C.
( )
3
2
'523
yx=-. D.
( )
3
2
2
'23
5
yx=-
.
Câu 26: Phương trình
1
2
log(3)1
x
-=-
có nghiệm là:
A.
3.
x
=
B.
5.
x
=
C.
2
x
=
. D.
1.
x
=
Câu 27: Hình trụ có chu vi đáy là
8
p
và chiều cao
6
h
=
. Diện tích xung quanh của hình trụ là
A.
12.
xq
S
p
= B.
24.
xq
S
p
= C.
xq
S
p
= D.
48.
xq
S
p
=
Câu 28: Đường hypebol (H) là đồ thị của hàm số
axb
y
cxd
+
=
+
(xem hình vẽ). Hỏi đó là hàm số nào ?
A.
3
1
x
y
x
-
=
+
. B.
23
1
x
y
x
+
=
+
. C.
3
1
x
y
x
+
=
-
. D.
3
1
x
y
x
+
=
+
.
Câu 29: Cho khối tứ diện
ABCD
có diện tích
BCD
D
bằng
2
32
a
và thể tích
3
216
Va
=
. Tính khoảng
cách h từ điểm A đến mặt phẳng
()
BCD
.
A.
27
ha
=
. B.
27
4
a
h =
. C.
9
4
a
h =
. D.
81
4
a
h =
.
Trang 4/6 - Mã đề 182
Câu 30: Thu gọn biểu thức
4
loglog256
a
a
P =
, (01)a<¹ ta được
A.
2(1log2)
a
P =+
. B.
2(12log2)
a
P =+
. C.
2(1log2)
a
P =-
. D.
2(12log2)
a
P =-
.
Câu 31: Cho hàm số
21
1
x
y
x
+
=
-
. Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số trên đoạn
[ ]
2;4
lần lượt là
A.
5;3Mm==
. B.
4;9Mm==
. C.
9
;-3
2
Mm
==
. D.
2
-;-2.
9
Mm
==
Câu 32: Cho phương trình
12
3315
xx+-
-=
. Đặt
3(0)
x
tt=>
ta nhận được phương trình nào ?
A.
2
39150tt+-=
. B.
2
530tt--=
. C.
2
530tt-+=
. D.
2
530tt+-=
.
Câu 33: Cho hàm số
23
4
x
y
x
-
=
+
có đồ thị
()H
và đường thẳng
()d
có phương trình
2yx=+
. Gọi m
là số giao điểm của đường thẳng
()d
và
()H
. Chọn khẳng định đúng.
A.
2
m = . B.
1
m = . C.
3
m = . D.
0
m = .
Câu 34: Cho hàm số
2
2
1
x
y
xmx
-
=
-+
với
m
là tham số. Đồ thị hàm số đã cho không có tiệm cận đứng
khi
A.
2
m <- hoặc
2
m > .
B.
2
m =- .
C. 22m. D.
2
m = .
Câu 35: Cho hàm số
3
3yxx
=-
. Đồ thị hàm số có hai điểm cực đại và cực tiểu,với giá tri cực đại, giá
trị cực tiểu lần lượt là a và b . Khẳng định đúng là:
A.
.1
ab=- B.
0
ab-= . C.
0
ab+=. D.
.4
ab=
Câu 36: Cho hàm số
4
mx
y
xm
+
=
+
. Chọn khẳng định đúng.
A. Hàm số đồng biến trên từng khoảng xác định khi
22
m-<<.
B. Hàm số nghịch biến trên từng khoảng xác định khi
22
m-<< .
C. Hàm số đồng biến trên từng khoảng xác định khi
2
m >- .
D. Hàm số nghịch biến trên từng khoảng xác định khi
2
m <- hoặc
2
m > .
Câu 37: Bất phương trình
2
22
log9.log100xx--> có tập nghiệm là (0;)a và
(b;)+¥
. Tính
.
ab.
A.
.512.
ab=
B.
.0.
ab= C.
.1024.
ab=
D.
.2048.
ab=
Câu 38: Cho đồ thị hàm số
42
yaxbxc=++
như hình vẽ bên dưới. Chọn khẳng định sai.
A.
0
ac < . B.
0
c < . C.
0
ab > . D.
0
ab < .
Câu 39: Cho hình chóp
.
SABCD , ABCD là hình vuông cạnh
a
, SA vuông góc với đáy, góc giữa
SC và đáy là
0
60
. Bán kính mặt cầu ngoại tiếp hình chóp đã cho có độ dài là
A. 22.Ra= B. 23.Ra= C. 2.Ra= D. 3.Ra=
Trang 5/6 - Mã đề 182
Câu 40: Hình tứ diện diện đều ABCD cạnh
a
có chiều cao là:
A.
6
6
a
. B.
3
3
a
. C.
3
6
a
. D.
6
3
a
.
Câu 41: Cho hình chóp tam giác
.
SABC có thể tích
3
324Vcm=
. Gọi M, N lần lượt là trung điểm
của cạnh SA, SB. Tính thể tích V của khối đa diện ABCMN .
A.
3
243Vcm=
. B.
3
126Vcm=
. C.
3
81Vcm=
. D.
3
162Vcm=
.
Câu 42: Tính đạo hàm của hàm số
( )
2
ln53yxx=+- ta được
A.
2
2
'
53
x
y
xx
-
=
+-
. B.
2
32
'
53
x
y
xx
+
=
+-
. C.
2
1
'
53
y
xx
=
+-
. D.
2
32
'
53
x
y
xx
-
=
+-
.
Câu 43: Cho hàm số
()
yfx=
có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của
m
để
phương trình
()
fxm=
có ba nghiệm phân biệt trong đó có hai nghiệm âm và một nghiệm dương?
A.
2.
B.
0.
C.
1.
D.
3.
Câu 44: Cho hàm số
322
()(1)5()fxxaxbxab
=+-+-+
. Hỏi có bao nhiêu giá trị nguyên của tham số
a và b để hàm số đã cho luôn có hai điểm cực trị.
A. 5. B. Vô số. C. 0. D. 2019.
Câu 45: Cho hình chóp
.
SABCD , ABCD là hình thang cân, đáy lớn
AB
bằng 4 lần đáy nhỏ CD
chiều cao của đáy bằng
a
. Bốn đường cao của bốn mặt bên ứng với đỉnh S bằng nhau và bằng b .
Thể tích hình chóp là
A.
2
22
5
4.
24
a
Vba=- B.
2
22
5
4.
24
a
Vba=- C.
2
22
4.
24
a
Vba=- D.
2
22
5
.
8
a
Vba=-
Câu 46: Cho hàm số có đạo hàm và liên tục trên . Biết rằng đồ thị hàm số như
dưới đây.
Giá trị lớn nhất của hàm số trên đoạn là:
A. B. C.
[ ]
() ()
1;2
max1.gxg
-
=
D.
(
)
yfx
=
¡
(
)
/
yfx
=
6
4
2
2
x
y
3
O
1
-1
-1
2
5
[ ]
(
)
1;2
max
gx
-
(
)
(
)
2
gxfxxx
=--
[
]
1;2
-
[ ]
(
)
(
)
1;2
max0.
gxg
-
=
[]
(
)
(
)
1;2
max2.
gxg
-
=
[]
(
)
(
)
1;2
max1.
gxg
-
=-
Trang 6/6 - Mã đề 182
Câu 47: Cho hàm số đa thức
()yfx=
xác định và liên tục trên ¡ có đồ thị
()
'
fx
như hình bên
dưới.
Hỏi hàm số
(5)yfx=-
đồng biến trên khoảng nào được liệt kê dưới đây ?
A.
( )
;1
-¥
. B.
( )
3;8
. C.
( )
;5
-¥
. D.
( )
5;
+¥
.
Câu 48: Cường độ ánh sáng đi qua một môi trường khác không khí, chẳng hạn như nước, sương
mù, ...sẽ giảm dần tùy theo độ dày của môi trường và một hằng số
m
gọi là khả năng hấp thu tùy
thuộc môi trường theo công thức như sau:
0
x
IIe
m
-
=
với x là độ dày của môi trường đó, tính bằng
mét. Biết rằng nước biển có
1,4
m
=
. Hãy tính xem cường độ ánh sáng giảm đi bao nhiêu lần từ độ
sâu 2 mét xuống đến 20 mét ?
A.
10
7,7947.10
lần. B.
10
8,7947.10
lần. C. 10 lần. D.
10
6,7947.10
lần.
Câu 49: Cho hai số thực không âm
,xy
thỏa mãn
2
2
21
21log
1
y
xxy
x
+
+-+=
+
. Tìm giá trị nhỏ nhất
m
của
212
421.
x
Pexy
-
=+-+
A.
1
.
2
m =- B.
e3.
m =- C.
1.
m =- D. e.m =
Câu 50: Cho mặt cầu có đường kính
2ABR=
. Trên
AB
lấy
I
sao cho
(02)AIhhR=<<
, một mặt
phẳng vuông góc với
AB
tại
I
cắt mặt cầu theo đường tròn
(C)
. Xác định vị trí của
I
để thể tích
khối nón đỉnh A , đáy là đường tròn
(C)
đạt giá trị lớn nhất thì độ dài
AI
là
A.
2
.
3
R
AI
=
B.
5
.
3
R
AI = C.
.
3
R
AI
=
D.
4
.
3
R
AI
=
----------- HẾT ----------
Học sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm
Họ và tên học sinh:................................................................. Số báo danh:............................
1
SỞ GD&ĐT KIÊN GIANG
TRƯỜNG THPT LONG THẠNH
THI HỌC KỲ I – NĂM HỌC 2019 - 2020
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm:
182 268 386 475 Ghi chú
1
B
A
D
C
2
D
C
D
C
3
A
A
B
B
4
A
D
B
D
5
C
D
D
D
6
A
C
C
B
7
D
B
A
B
8
D
B
B
A
9
B
A
A
D
10
D
C
C
D
11
B
C
A
D
12
C
B
C
A
13
A
C
D
D
14
B
A
C
B
15
B
C
C
D
16
C
D
C
C
17
A
B
D
C
18
D
D
A
B
19
C
D
C
B
20
A
D
D
D
21
D
D
A
A
22
A
D
D
B
23
C
D
D
A
24
D
B
D
D
25
C
D
B
C
26
B
A
C
C
27
D
C
A
A
28
D
B
A
A
29
D
B
D
C
30
B
B
A
D
31
A
C
D
C
32
B
A
B
A
33
D
A
C
C
34
C
C
C
A
35
C
B
A
B
36
B
C
C
D
37
A
B
D
D
38
C
C
B
A
39
C
B
B
A
40
D
D
B
A
41
A
C
D
B
42
D
D
A
B
43
C
A
D
D
44
B
D
A
C
45
B
A
B
B
46
C
A
C
C
47
A
A
A
A
48
B
B
B
C
49
A
D
B
D
50
D
A
B
B
1
Hướng dẫn giải một số câu Vận dụng – Vận dụng cao
Câu: Cho hàm số
4mx
y
xm
+
=
+
. Chọn khẳng định đúng.
Hướng dẫn giải: Ta có:
2
''2
2
4
;04022
()
m
yymm
xm
-
=<Û-<Û-<<
+
Câu: Cho hàm số
3
3yxx=-. Đồ thị hàm số có hai điểm cực đại và cực tiểu,với giá tri cực đại, giá
trị cực tiểu lần lượt là a và b . Khẳng định đúng là:
Hướng dẫn giải: Ta có:
'2
3301yxx=-=Û=± . Hàm số đạt cực đại tại
1
x =- , đạt giá trị cực đại
2y =
, đạt cực tiểu tại
2y =-
. Vậy 2;2ab==- nên 0ab
+=
.
Câu : Hình vẽ bên là đồ thị của hàm số
()
.yfx= Gọi S là tập hợp các số nguyên dương của tham
số m để hàm số
( )
1yfxm=-+ có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
Hướng dẫn giải: Đồ thị hàm số
( )
1yfx=- nhận được bằng cách tịnh tiến đồ thị hàm số
()
yfx=
sang phải 1 đơn vị nên không làm thay đổi tung độ các điểm cực trị.
Đồ thị hàm số
( )
1yfxm=-+ nhận được bằng cách tịnh tiến đồ thị hàm số
( )
1yfx=-lên trên m đơn
vị nên ta có:
2;3,6
CDCTCT
ymymym=+=-+=-+
2
Đồ thị hàm số
(
)
1
yfxm
=-+
nhận được bằng cách từ đồ thị hàm số y = f\left( x-1 \right)+m lấy đối
xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
Để đồ thị hàm số có 5 cực trị
{
}
603363;4;5
mmmmÛ-+<£-+Û£<ÞÎ
{
}
3;4;534512.
SÞ=Þ++=
Câu: Cho hàm số có đạo hàm và liên tục trên . Biết rằng đồ thị hàm số như
dưới đây.
Giá trị lớn nhất của hàm số trên đoạn là:
Hướng dẫn giải: nên
'''
()()210()211;2.
gxfxxfxxxx
=--=Û=+Û==
Xét dấu
'
()0
gx
<
trên đoạn
[
]
1;2
vậy
[ ]
(
)
(
)
1;2
max1.
gxg
-
=
Câu : Cho hàm số
2
2
1
x
y
xmx
-
=
-+
với
m
là tham số. Đồ thị hàm số đã cho không có tiệm cận đứng
khi
Hướng dẫn giải: Đồ thị hàm số không có tiêm cận đứng khi
2
10
xmx
-+=
vô nghiệm, tức
2
4022
mm
-<Û-<<
.
Câu : Cho hàm số
yfx
có bảng biên thiên như hình vẽ
(
)
yfx
=
¡
(
)
/
yfx
=
6
4
2
2
x
y
3
O
1
-1
-1
2
5
[ ]
(
)
1;2
max
gx
-
(
)
(
)
2
gxfxxx
=--
[
]
1;2
-
(
)
(
)
2
gxfxxx
=--
3
Hàm số

2
53
2
22
gxfxx



nghịch biến trên khoảng:
Hướng dẫn giải: Ta có
()
2
553
42.
222
gxxfxx
æöæö
¢¢
=---
ç÷ç÷
èøèø
Xét
()
2
2
2
5
5
8
40
2
53159
0221;;;1;.
53
22484
20
53
22
23
22
x
x
gxxxx
fxx
xx
é
=
ê
é
-=
ê
ê
ìü
ê
¢
ê
=ÛÛ--=-ÛÎ-
íý
ê
æö
îþ
ê
¢
--=
ê
ç÷
ê
èø
ë
ê
--=
ê
ë
Bảng biến thiên
Dựa vào bảng biến thiên, ta chọn
5
1;.
4


(So sánh các đáp án)
Câu: Cho hai số thực không âm thỏa mãn
2
2
21
21log
1
y
xxy
x
+
+-+=
+
. Tìm giá trị nhỏ nhất
m
của
212
421.
x
Pexy
-
=+-+
Hướng dẫn giải: Ta biến đổi PT về dạng hàm đặc trưng:
22
222
2
22
22
22
'
2
21
1
21log21log(21)log(x1)
12
2x42log(1)log(21)2
2(1)log2(1)log(21)21
1
()log,0.()10
.ln2
y
xxyxxyy
x
xxyy
xxyy
fttttft
t
+
+-+=Û+-+=+-+
+
Û+++=++
Û+++=+++
=+>=+>
Hàm
()
ft
đồng biến trên
(0;)
+¥
.
222122
(2(x1))(21)2(x1)2142(1)2
x
ffyyPexx
-
+=+Û+=+Û=+-++
Tìm GTNN của P ta được kết quả
1
2
p
³-
Câu : Tìm tất cả cá giá trị của
m
để phương trình
2
2
2
log8log840
xxm
--+=
vô nghiệm trên đoạn
[
]
1;4
Hướng dẫn giải: Ta có
22
222
2
log8log8404log8log84
xxmxxm
--+=Û-=-
4
2
22
log2log21
xxm
Û-=-
. Đặt
[
]
[
]
2
log,1;40;2
txxt=ÎÞÎ .
Ta có
2
()2
fttt
=-
thì
[ ]
[ ]
0;2
0;2
max()0,min()1
ftft
==-
.
Do đó để phương trình
2
221
ttm
-=-
vô nghiệm trên
[
]
0;2
thì
1
210
2
211
0
m
m
m
m
é
->
>
é
ê
Û
ê
ê
-<-
ë
<
ë
Câu: Cho hình chóp .
SABCD
,
ABCD
là hình thang cân, đáy lớn
AB
bằng 4 lần đáy nhỏ
CD
chiều
cao của đáy bằng
a
. Bốn đường cao của bốn mặt bên ứng với đỉnh
S
bằng nhau và bằng
b
. Thể
tích hình chóp là
Hướng dẫn giải: (Tự vẽ hình nhe !)
H là chân đường cao của hình chóp thì H cách đều các cạnh của đáy, H nằm trong đáy. Suy ra đáy
có đường tròn nội tiếp tâm H là trung điểm MN với M, N lần lượt là trung điểm AB và CD, MN = a.
Đường tròn tiếp xúc BC tại E thì HM = HN = HE =
2
a
là bán kính đường tròn, ta có SE = SM = SN
= b (
2
a
b>
) suy ra
22
1
4
2
SHba
=-
. Đặt CN = x, BM = 4x, CE = x, BE= 4x. Tam giác HBC vuông
ở H nên
22
2
5
4,2
4424
ABCD
aaaa
xxCDABaS=Þ=Þ==Þ=
. Ta có kết quả
2
22
5
4.
24
a
Vba
=-
Câu: Cho mặt cầu có đường kính
2
ABR
=
. Trên
AB
lấy
I
sao cho
(02)
AIhhR
=<<
, một mặt
phẳng vuông góc với
AB
tại
I
cắt mặt cầu theo đường tròn
(C)
. Xác định vị trí của
I
để thể tích
khối nón đỉnh
A
, đáy là đường tròn
(C)
đạt giá trị lớn nhất thì độ dài
AI
là
Hướng dẫn giải: (tự vẽ hình nhe) Goi EF là đường kính của ( C).
Ta có:
2
.(2)
IEIAIBhRh
==-
.
Bán kính của (C)
(2)
rIEhRh
==-
.
Thể tích hình nón đỉnh A là
2
2
1
(2)(0h2)
33
h
VrhRhR
p
p
==-<<
'2
max
44
(43)0
333
RR
VRhhhVhIA
p
=-=Û=ÞÛ==
Câu: Tìm tất cả giá trị thực của m để hàm số
sin2019
x
yx
m
=-+
nghịch biến trên toàn trục số.
Hướng dẫn giải: Ta có
1
'cosyx
m
=-
. Để hàm số nghịch biến trên toàn trục số thì '0yx
£"Î
¡
1
cos0xx
m
Û-£"Î
¡
. Mà |cos|1xx
£"Î
¡
, từ đó suy ra
1
101
m
m
³Û<£
.
Câu: Hàm số
23
(2019)(2020)
yxx=+- có bao nhiêu điểm cực trị ?
Hướng dẫn giải: Ta có
322
'2(2019)(2020)3(2019)(2020)
yxxxx=+-++-
[
]
2
'(2019)(2020).2(2020)3(2019)
yxxxx=+--++ .
Suy ra phương trình
'0
y
=
có 2 nghiệm phân biệt và một nghiệm kép.
Vậy hàm số đã cho có 2 điểm cực trị.
5
Câu: Cho hàm số
322
()(1)5()fxxaxbxab=+-+-+. Hỏi có bao nhiêu giá trị nguyên của tham số a
và b để hàm số đã cho luôn có hai điểm cực trị.
Hướng dẫn giải: Ta có
22
'()32(1)fxxaxb=+-+ .
Ta thấy
2
3.(1)0
bb
éù
-+<"Î
ëû
¡ .
Do đó phương trình
'0
y= luôn có 2 nghiệm phân biệt.
Vậy có vô số giá trị nguyên của a và b thỏa yêu cầu bài toán.
Câu: Một trang trại trồng rau sạch theo tiêu chuẩn VietGap tại địa điểm B để cung cấp cho siêu thị
A đặt trên hòn đảo cách xa đất liền 160km (đoạn AH trên hình vẽ). Người ta dự định xây một trạm
tàu tại vị trí C để vận chuyển rau xanh ra đảo. Biết rằng tốc độ vận chuyển của xe chở trên đất liền là
70km/h và của tàu hàng trên biển là 40km/h. Hỏi phải chọn điểm C cách B bao xa để thời gian vận
chuyển rau xanh ra đảo là ít nhất, biết khoảng cách từ trang trại B đến siêu thị A trên đảo là 300km.
(kết quả làm tròn đến 2 chữ số thập phân)
Hướng dẫn giải: Ta có
22
30016020161
HB =-=
.
Đặt
( )
()0;20161
BCxkmx=ÞÎ
và 20161HCx=-
Đoạn
( )
2
2
16020161ACx=+-
Tổng thời gian vận chuyển là
( )
2
2
16020161
()
7040
x
x
tx
+-
=+
Tìm min của hàm số
()tx
trên
( )
0;20161
, ta được
min
6,91142,36thkhixkm»»
.
Câu: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số
2
3
499
x
y
xx
+
=
--+
là
Hướng dẫn giải: Ta viết lại
31
(3)(34)
3.(34)
x
y
xx
xx
+
==
+-
+-
Ta có tập xác định
33
3;;
44
D
æöæö
=È+¥
ç÷ç÷
èøèø
.
Từ đó ta thấy hàm số có 2 tiệm cận đứng là
3
3,
4
xx
=-=
và 1 tiệm cận ngang
0
y = .
Vậy tổng cộng có 3 đường tiệm cận.
6
Câu: Cho đồ thị hàm số
42
yaxbxc=++
như hình vẽ bên dưới. Chọn khẳng định sai.
Hướng dẫn giải: Ta thấy đồ thị hàm số có 3 điểm cực trị.
Do đó phương trình
32
2
0
'422(2)0
2
x
yaxbxxaxb
b
x
a
=
é
ê
=+=+=Û
-
ê
=
ë
có 3 nghiệm phân biệt.
Suy ra
00
2
b
ab
a
-
>Û<
.
Câu: Cho hàm số đa thức
()yfx=
xác định và liên tục trên ¡ có đồ thị
()
'
fx
như hình bên dưới.
Hỏi hàm số
(5)yfx=-
đồng biến trên khoảng nào được liệt kê dưới đây ?
Hướng dẫn giải: Từ đồ thị ta suy ra
'()(3)(2)(0)fxaxxxa=+-<
.
Mà đề cho
(5)yfx=-
, suy ra
[ ]
(5)''(5)()(5)(8)(3)0
fxfxaxxx-=--=----=
Phương trình này có 3 nghiệm là 3; 5; 8 và hệ số
()(1)(1)(1)0a----<
.
Lập bảng biến thiên, suy hàm số
(5)yfx=-
đồng biến trên
(;3)-¥
và
(5;8)
.
Vậy chọn hàm số đồng biến trên khoảng
(;1)-¥
.
Câu: Có bao nhiêu giá trị nguyên của tham số
[ ]
2019;2019a Î- để hàm số
4223
2yxaxaa=--+ tiếp
xúc với trục hoành tại hai điểm phân biệt.
Hướng dẫn giải: Từ đề bài ta tính được
32
'444()yxaxxxa=-=-.
Hàm số đã cho là hàm bậc 4 nên muốn tiếp xúc với trục hoành tại 2 điểm thì hàm số phải có 3 cực
trị. Hay phương trình
'0
y
=
có 3 nghiệm phân biệt.
Ta có
2
0
'0
x
y
xa
=
é
=Û
ê
=
ë
. Do đó 0a > và 3 điểm cực trị là
0,
xxa==± .
7
Hàm số tiếp xúc với trục hoành nên
32
0
()020
2
a
yaaa
a
=
é
=Û-=Û
ê
=
ë
.
Vậy 2a = (vì 0a > )
Câu: Cường độ ánh sáng đi qua một môi trường khác không khí, chẳng hạn như nước, sương mù,
...sẽ giảm dần tùy theo độ dày của môi trường và một hằng số
m
gọi là khả năng hấp thu tùy thuộc
môi trường theo công thức như sau:
0
x
IIe
m
-
= với x là độ dày của môi trường đó, tính bằng mét.
Biết rằng nước biển có
1,4
m
=
. Hãy tính xem cường độ ánh sáng giảm đi bao nhiêu lần từ độ sâu 2
mét xuống đến 20 mét ?
Hướng dẫn giải: Từ công thức đề cho
0
x
IIe
m
-
= lần lượt áp dụng tại độ sâu 2 mét và 20 mét ta có:
20
2
IIe
m
-
= ;
200
20
IIe
m
-
= . Suy ra tỉ số
0
2
20
0
2
18
20
Ie
I
e
I
Ie
m
m
m
-
-
==
Với nước biển ta có
1,4
m
=
, tính được tỉ số
10
2
20
8,7947.10
I
I
» lần.
(Từ đó ta nhận thấy, khi xuống sâu 20 mét thì gần như không có ánh sáng dưới biển)
Câu: Cho hình chóp tứ giác .SABCD có đáy là hình vuông cạnh 2a . Biết hình chiếu vuông góc của
đỉnh S lên mặt phẳng đáy là điểm M trung điểm cạnh AD và tam giác SMB cân. Tính thể tích V của
khối chóp .SMBCD .
Hướng dẫn giải: Vì tam giác SMB vuông tại M nên chỉ có thể cân tại đỉnh M.
Do đó chiều cao hình chóp
22
(2)5
SMMBaaa==+=
Thể tích khối chóp .SMBCD là
3
11(2).2
..55
332
MBCD
aaa
VSSMaa
+
æö
===
ç÷
èø
Câu: Một hình nón có góc ở đỉnh bằng
0
60 và đường kính đường tròn đáy bằng 8a . Mặt phẳng
()
a
đi qua đỉnh của hình nón và cách tâm đường tròn đáy 2a . Tính diện tích S thiết diện của mặt phẳng
()
a
cắt hình nón đã cho.
Hướng dẫn giải: Chiều cao hình nón là
0
4
43
tan30
a
SIa
==
.
Ta có
22222
11111433
1:
11
a
IM
IHIMSIIHSI
=+Þ=-=
Ta có
22
2411
11
a
SMIMSI=+=
22
1622
22
11
a
EFMFIFIM==-=
Vậy diện tích thiết diện
2
1162224111922
..
2111111
SEF
aaa
S==
8
Câu: Cho hình chóp tam giác .SABCD có đáy là hình vuông cạnh 6a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp .SABCD
theo a.
Hướng dẫn giải: G là trọng tâm tam giác SAB, M là trung điểm AB,
163
.3
32
a
GMa==
K là tâm mặt đáy, bán kính mặt cầu ngoại tiếp
( )
2
2
22
62
321
2
a
RICKCKIaa
æö
==+=+=
ç÷
ç÷
èø
Vậy
( )
3
3
4
212821
3
Vaa
pp
==
| 1/21
| | Tải xuống

Có thể bạn quan tâm:

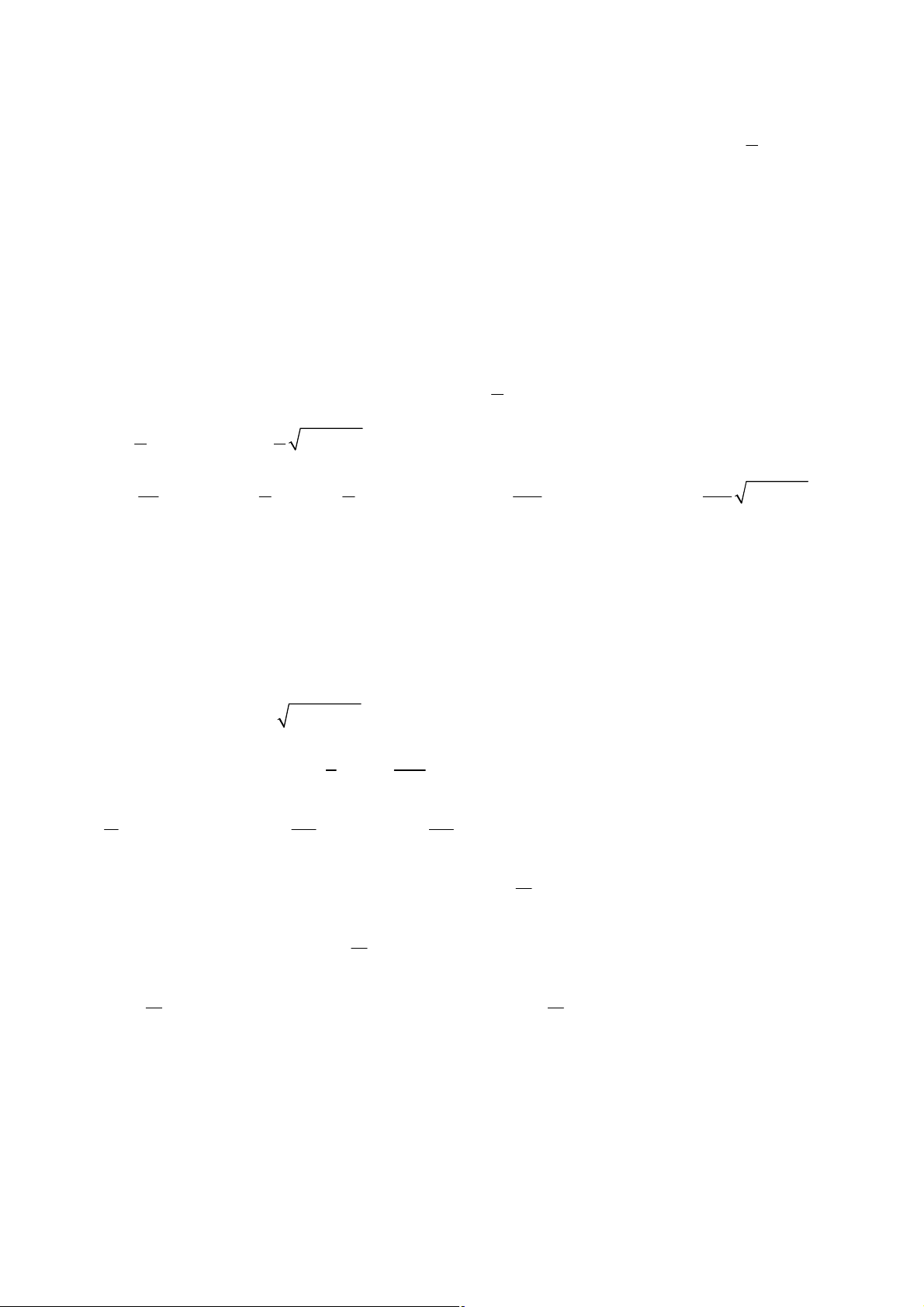
Preview text:

TRƯỜNG THPT LONG THẠNH
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 – 2020 TỔ: TOÁN MÔN THI: TOÁN 12
Thời gian làm bài: 90 phút (không kể thời gian giao đề) (Đề có 06 trang) Ngày thi: 14/12/2019 Mã đề 268
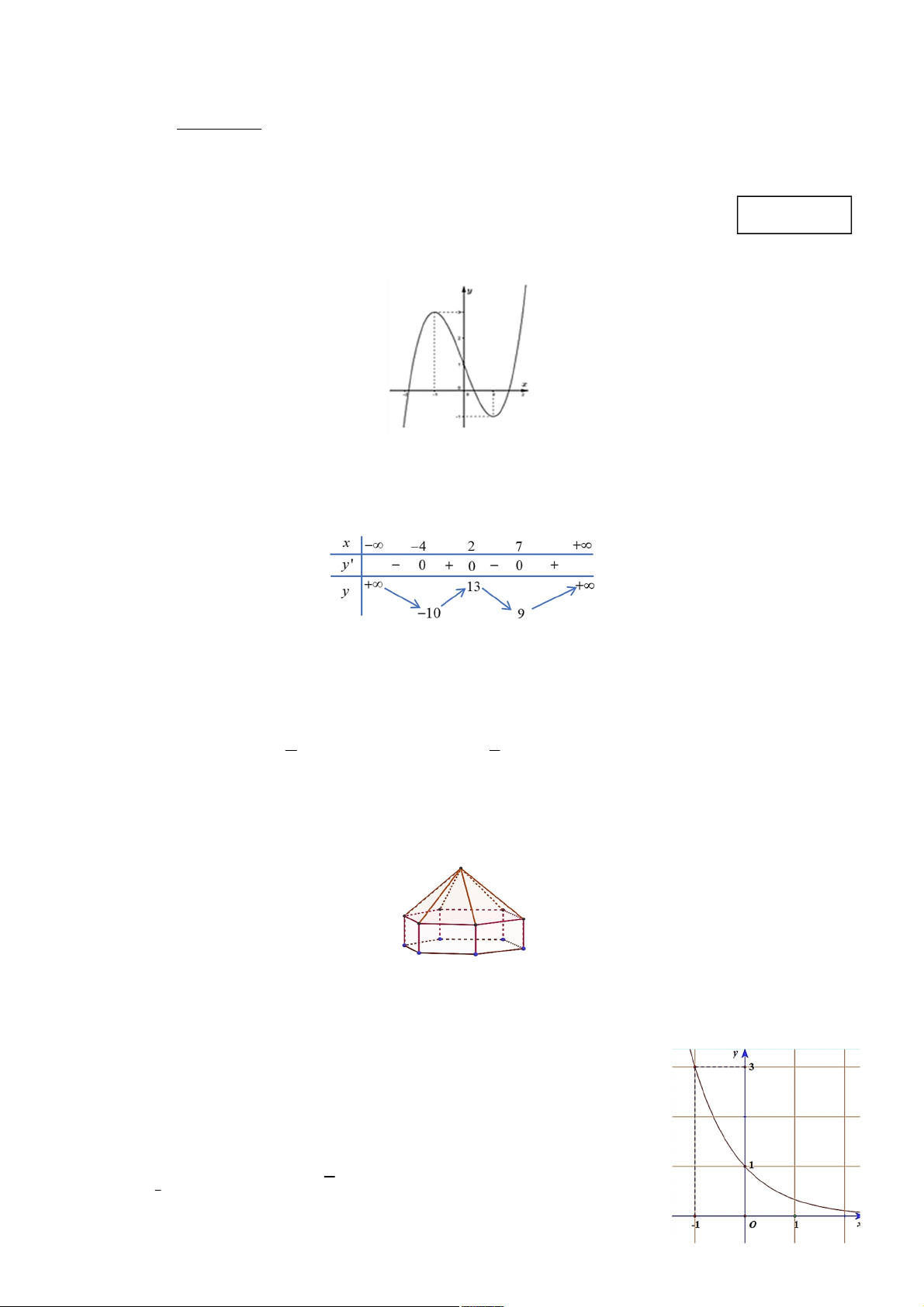
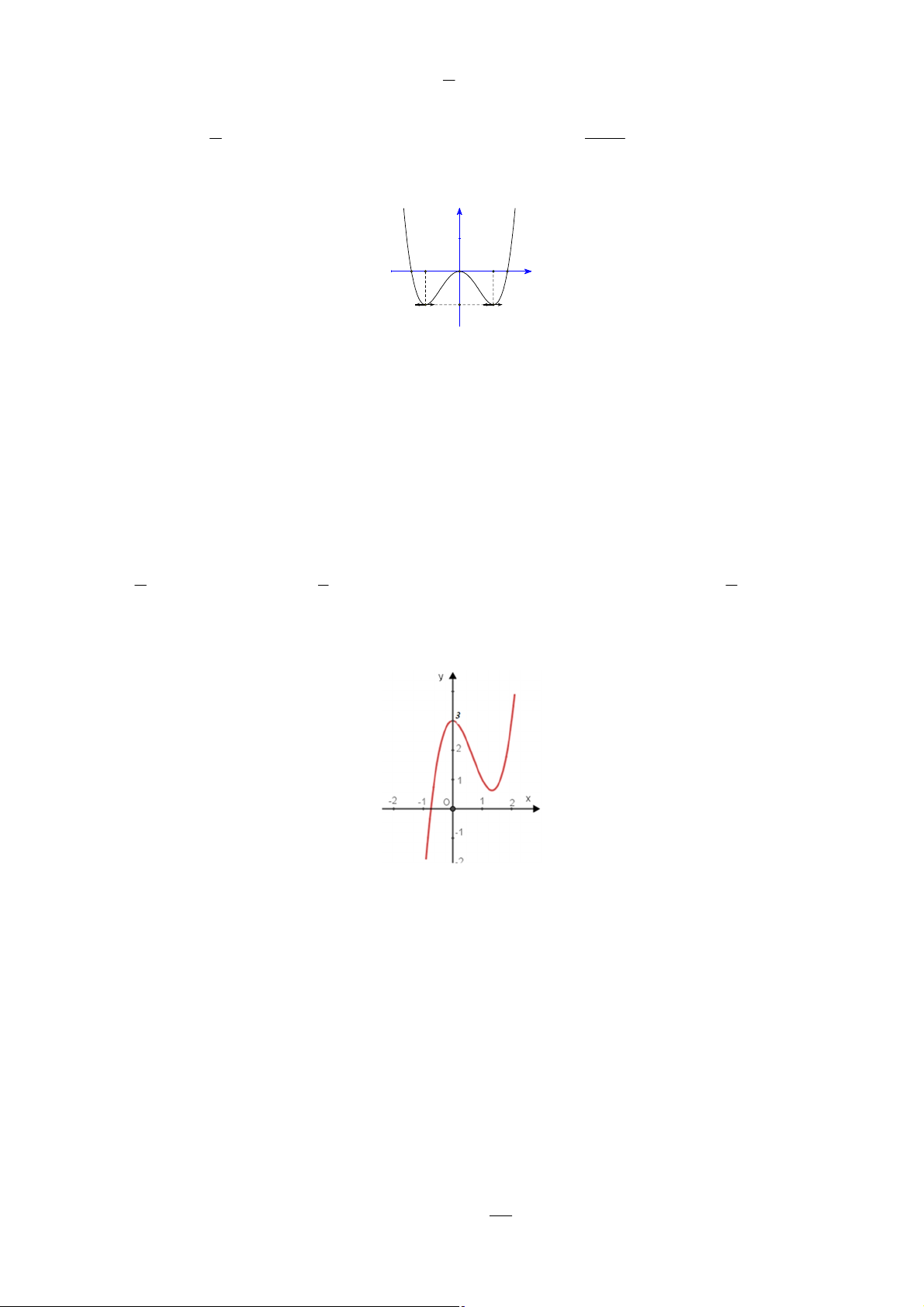
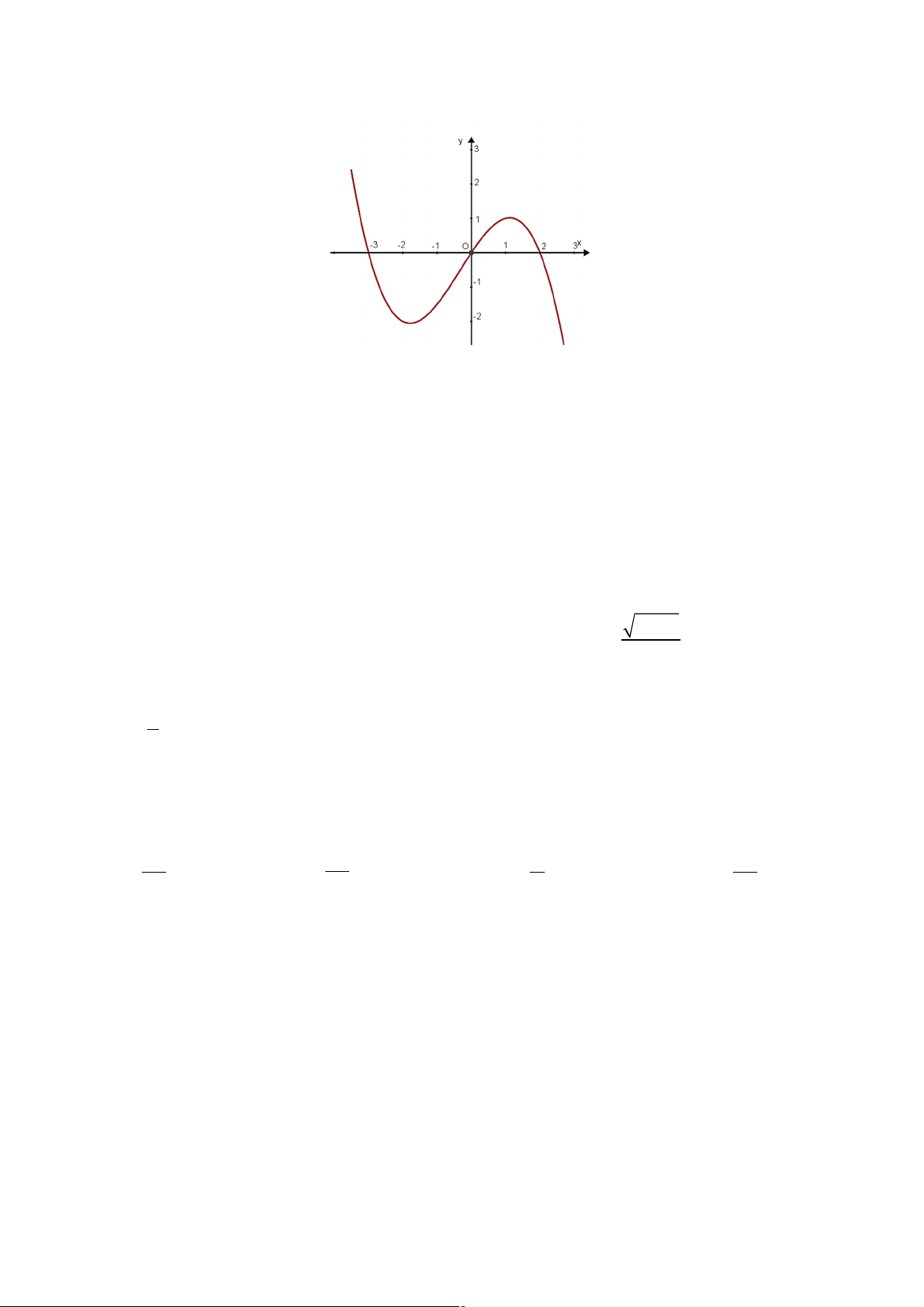
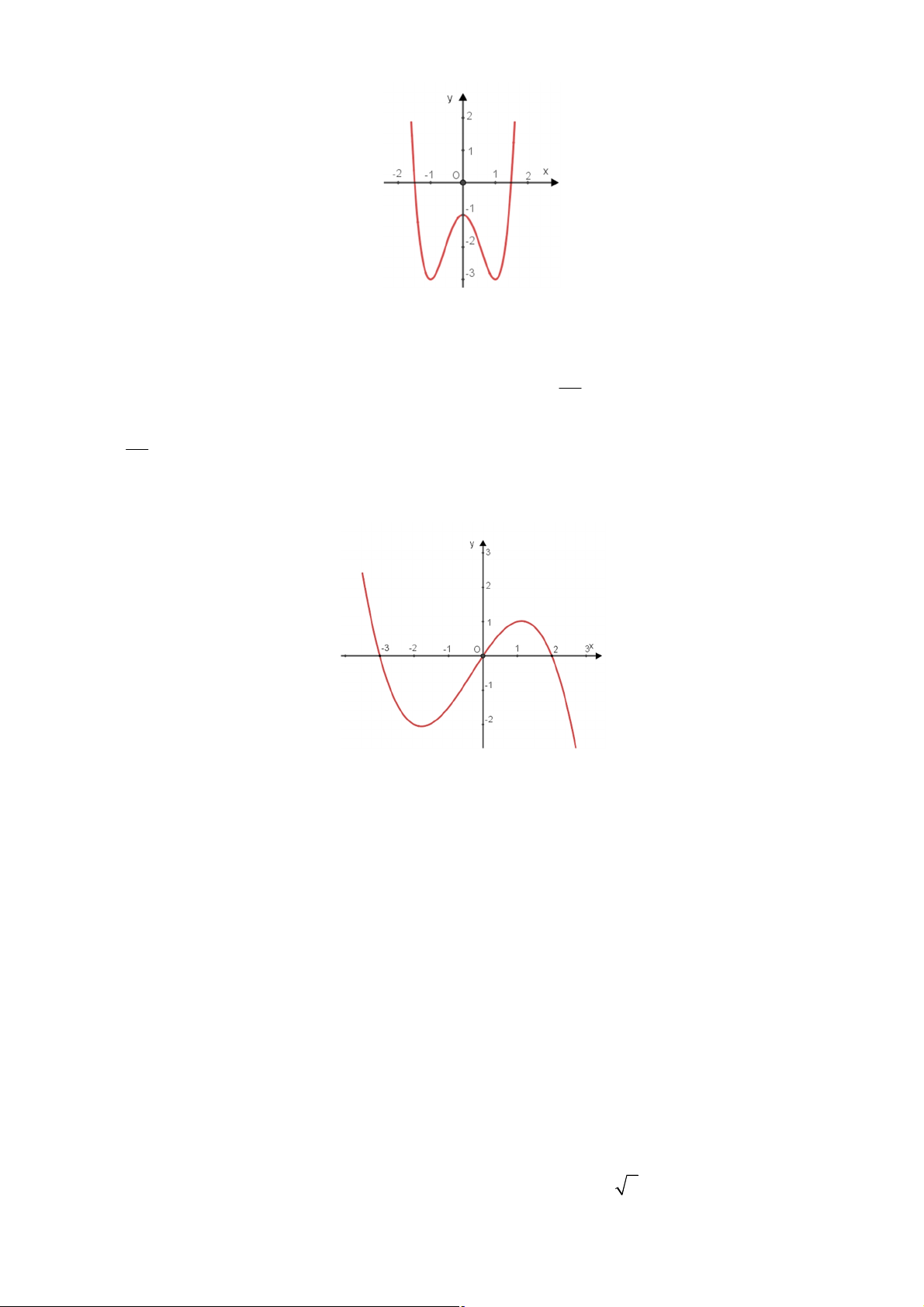
Câu 1: Đồ thị cho bên dưới là của một trong bốn hàm số dưới đây. Chọn khẳng định đúng
A. Hàm số bậc ba.
B. Hàm số bậc hai.
C. Hàm số bậc bốn.
D. Hàm số phân thức hữu tỉ.
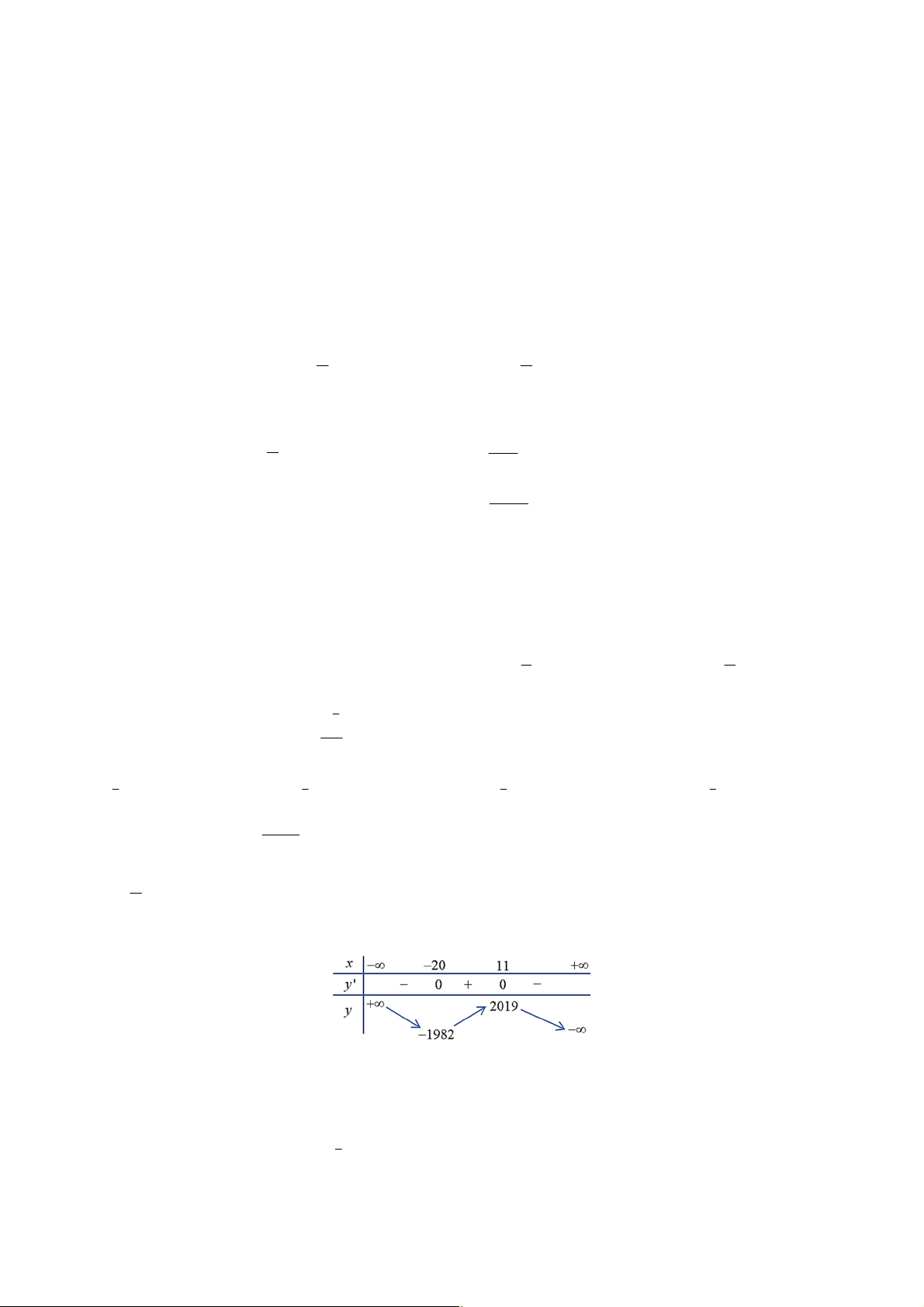
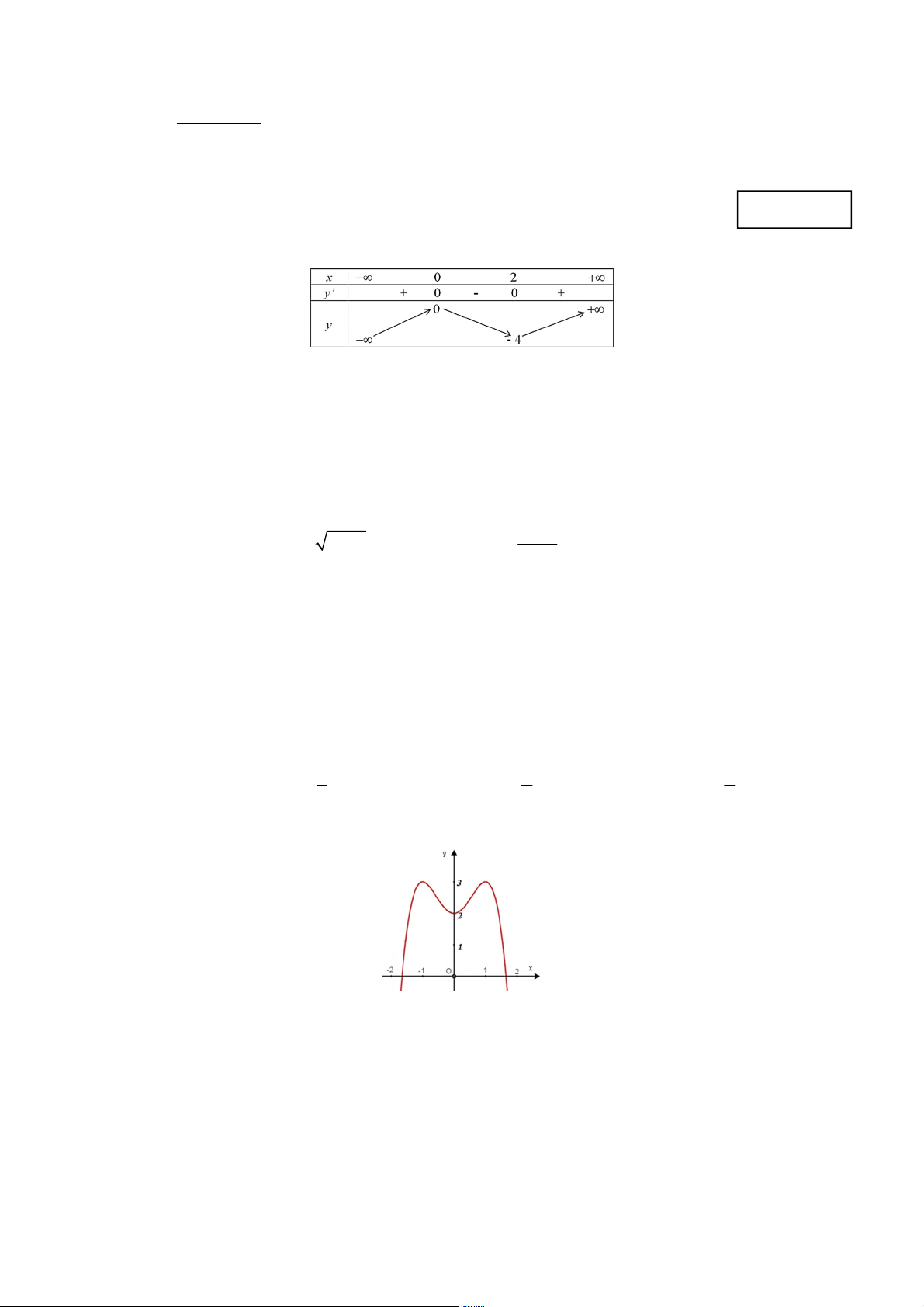
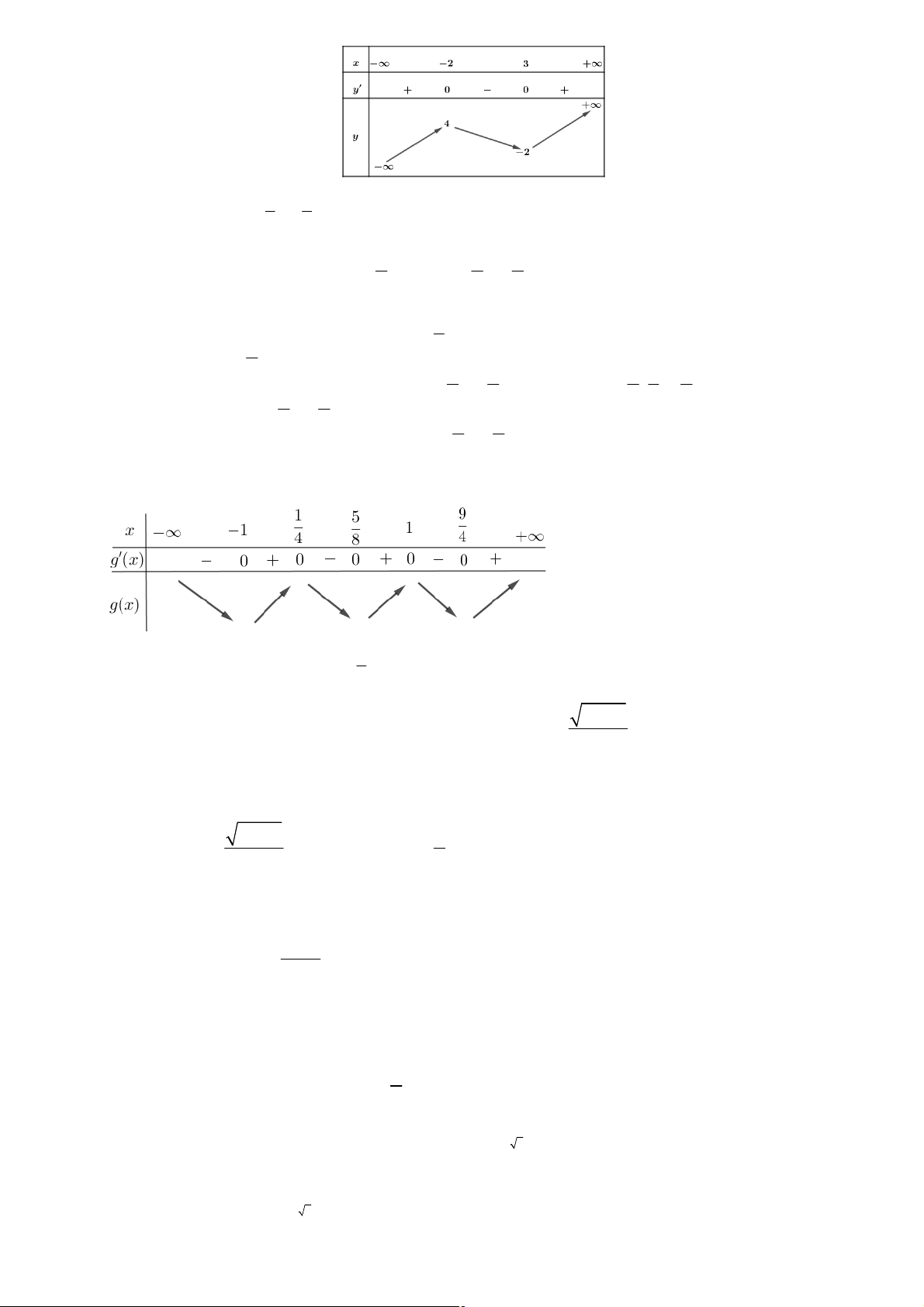
Câu 2: Cho hàm số y = f (x) có bảng biến thiên như hình bên dưới
Giá trị cực đại của hàm số đã cho bằng A. 9. B. 2. C. 13. D. 10 - .
Câu 3: Khối lăng trụ có diện tích đáy B, chiều cao h thì thể tích bằng A. Bh . B. 1 Bh . C. 1 Bh . D. 3Bh . 6 3
Câu 4: Khi xoay một tam giác vuông quanh một cạnh góc vuông, hình tròn xoay được tạo ra là : A. Hình chóp. B. Hình trụ. C. Hình lăng trụ. D. Hình nón.
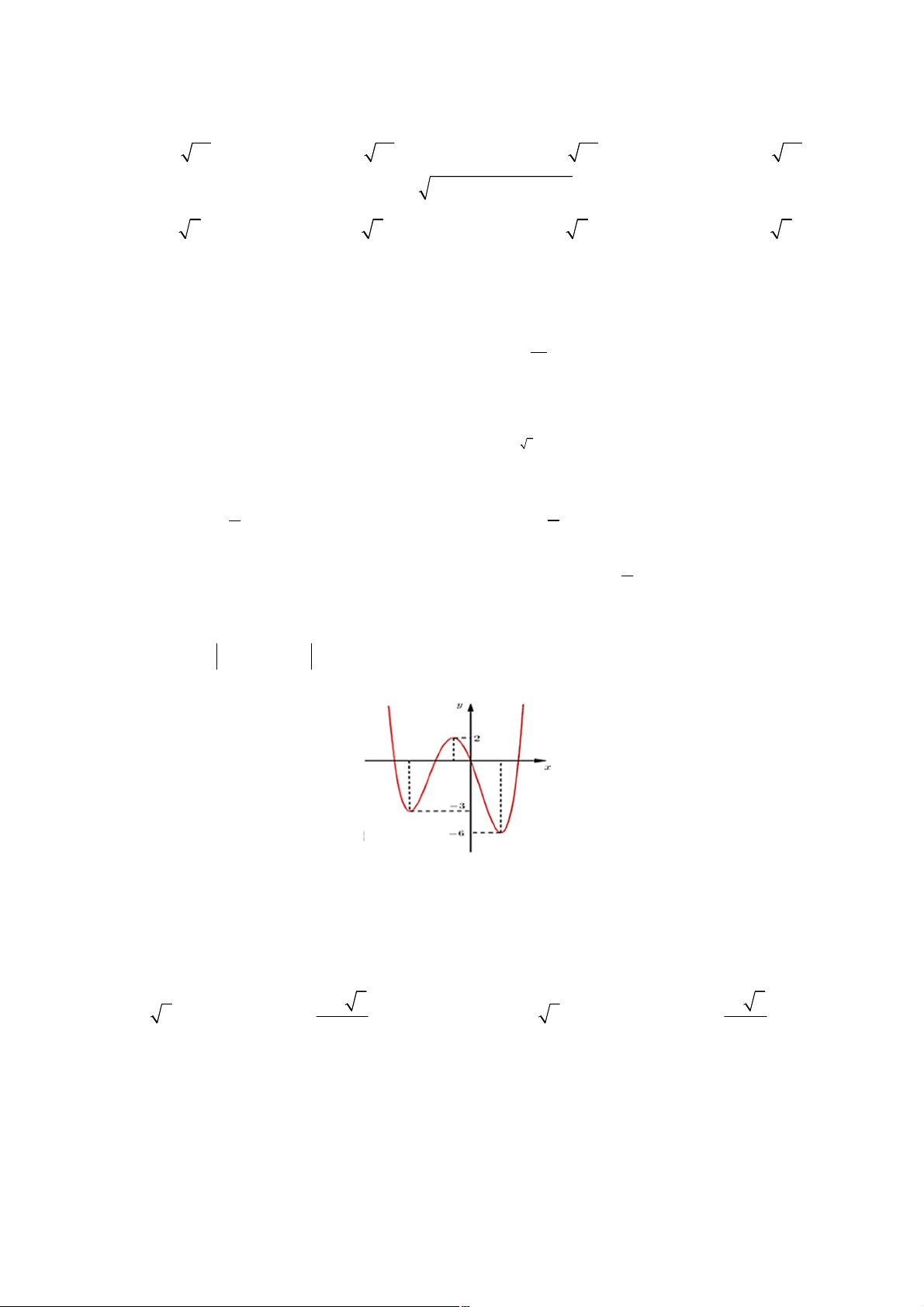
Câu 5: Hình đa diện như hình bên dưới có bao nhiêu cạnh ? A. 6. B. 18. C. 12. D. 24.
Câu 6: Có bao nhiêu loại khối đa diện đều ? A. Vô số. B. 4. C. 5. D. 6.
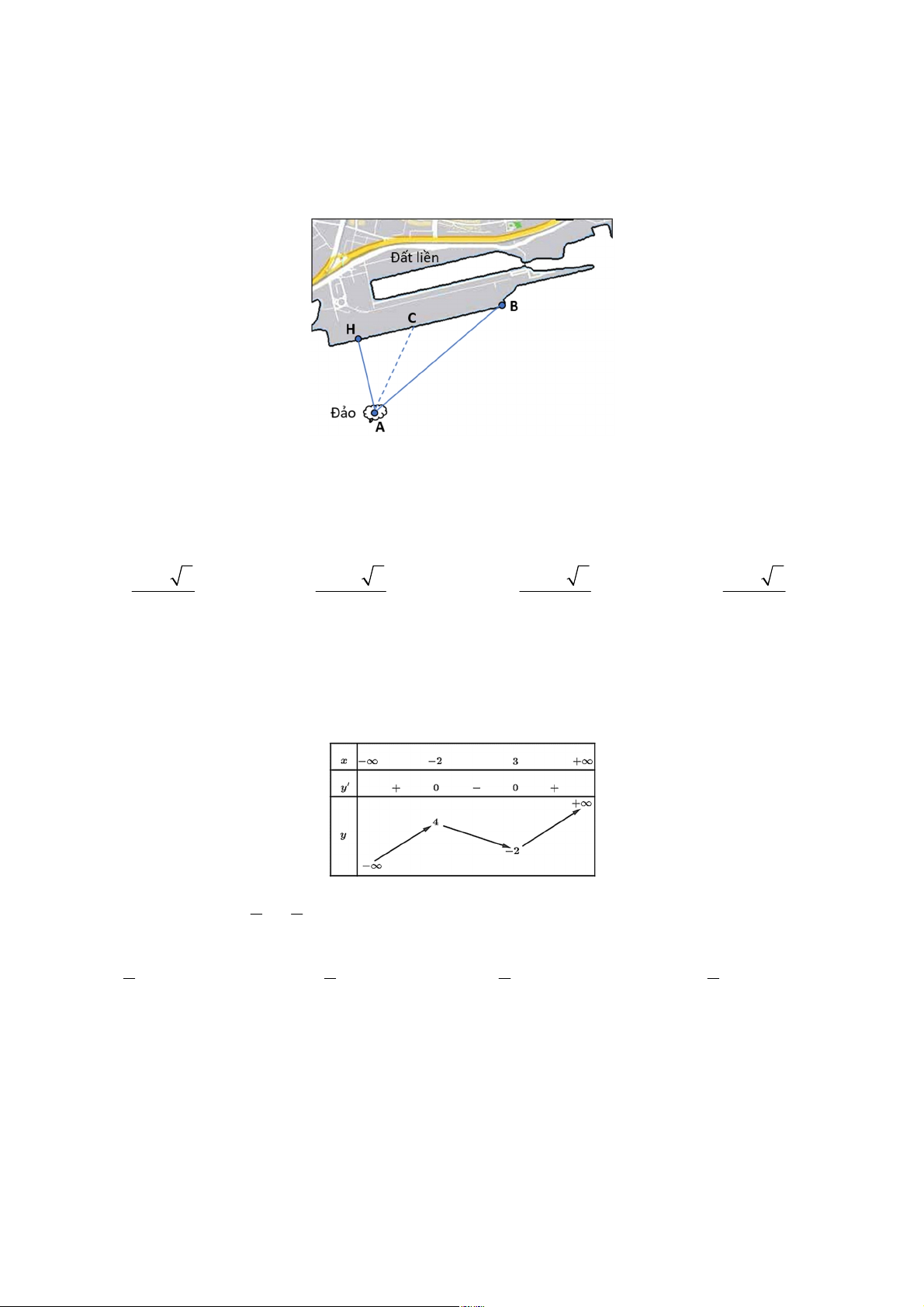
Câu 7: Đồ thị bên phải là của một trong bốn hàm số được liệt kê dưới
đây. Chọn khẳng định đúng. x A. æ ö y = log x. B. 1 y = . 1 ç ÷ è 3 ø 3
C. y = log x . D. 3 .x y = 3 Trang 1/6 - Mã đề 268 Câu 8: Cho hàm số 2
y = x - 2x + 3 . Giá trị nhỏ nhất của hàm số là A. 0 . B. 2 . C. 1. D. 3.
Câu 9: Giải bất phương trình 5x > 124 ta được
A. x > log 124 .
B. x < log 124 .
C. x > log 5 .
D. x < log 5 . 5 5 124 124
Câu 10: Phương trình 2x = 64 có nghiệm là A. x = 6 - . B. x = 32. C. x = 6. D. x = 5. Câu 11: Cho hàm số 3 2
y = x - 2x - 3 . Đồ thị hàm số cắt trục tung Oy tại điểm M có tọa độ là A. M (0;3) . B. M (0; -1). C. M (0; -3). D. M (3;1) .
Câu 12: Công thức tính thể tích khối cầu có bán kính R là A. 4 4 3 V = 4p R . B. 3 V = p R . C. 2 V = p R . D. 2 V = 4p R . 3 3
Câu 13: Với 0 < a ¹ 1 và b, c là số thực dương. Chọn khẳng định sai. æ b ö A. b
log b - log c = log .
B. ln = log b . a a a ç ÷ è c ø ln a a C. c
log b + log c = log (b + c) .
D. log = log c . a a a log a a
Câu 14: Tìm tập xác định của hàm số y ( x ) 3 7 - = - . A. ¡ \{ } 7 . B. (-¥;7) . C. ¡ \{ } 7 - . D. (7;+¥) .
Câu 15: Khối chóp có diện tích đáy B, chiều cao h thì công thức tính thể tích V là
A. V = Bh .
B. V = 3Bh . C. 1 V = Bh . D. 1 V = Bh . 3 6 3 4 a
Câu 16: Thu gọn biểu thức, A =
(a > 0) , kết quả đúng là 2 a 5 5 - 1 5 - A. 6 a . B. 6 a . C. 4 a . D. 4 a . + Câu 17: Cho hàm số x 2 y =
. Đồ thị hàm số có tiệm cận đứng là x -1 A. 1 x = . B. x = 1. C. x = -1 . D. x = 2. 2
Câu 18: Cho hàm số y = f (x) có bảng biến thiên như hình bên dưới.
Hỏi hàm số đã cho đồng biến trên khoảng nào ? A. (-¥;-20) . B. (11;+¥) . C. (-1982;2019) . D. (-20; ) 11 .
Câu 19: Giải bất phương trình log x - 4 ³ -3 . Ta được 1 ( ) 6 A. x ³ 220 . B. x > 220 .
C. 4 < x < 220 .
D. 4 < x £ 220 . Trang 2/6 - Mã đề 268
Câu 20: Một hình cầu có bán kính bằng 6cm . Một mặt phẳng đi qua tâm của mặt cầu. Tính diện
tích S thiết diện của mặt cầu và mặt phẳng. A. 2 S = 18p cm . B. 2 S = 9p cm . C. 2 S = 144p cm . D. 2 S = 36p cm .
Câu 21: Với a ,b,c là các số thực dương tùy ý và a khác 1. Đặt 8 4
P=log b +log b . Mệnh đề đúng là 2 a a A. P = 5log . b B. P = 7log . b C. P = 12log . b D. P = 8log . b a a a a
Câu 22: Giải phương trình 2
log (x + 7) = 4 ta được tập nghiệm 2 A. S = { } 3 . B. S = {- } 3 . C. S = {-9 } ;9 . D. S = {-3 } ;3 .
Câu 23: Cho hàm số f x = (x - x)5 2 ( ) 4
, f (x) có đạo hàm là A. 2
f '(x) = 5(2x - 4)(x - 4x). B. 2 4
f '(x) = 5(x - 4x) . C. 2 4
f '(x) = 5(2x - 4x)(x - 4x) . D. 2 4
f '(x) = 5(2x - 4)(x - 4x) . Câu 24: Cho hàm số 3 2
y = ax + bx + cx + d .Chọn khẳng định đúng:
A. Hàm số đồng biến trên ¡ khi y ' = 0 vô nghiệm hoặc nghiệm kép và a < 0.
B. Hàm số có một cực đại và một cực tiểu khi y ' = 0 có hai nghiệm phân biệt.
C. Hàm số không có cực trị khi y ' = 0 có nghiệm.
D. Hàm số nghịch biến trên ¡ khi y ' = 0 vô nghiệm hoặc nghiệm kép và a >0.
Câu 25: Hộp nước sơn hình trụ có kích thước như hình vẽ. Tính thể tích V của hộp nước sơn đó. A. 3 V = 24000 cm . B. 3 V = 96000 cm . C. 3 V = 96000p cm . D. 3
V = 24000p cm .
Câu 26: Trong các hàm số sau, hàm số nào là hàm số mũ ? 1 1 A. y = .
B. y = x . C. 2 y x- = . D. 3 y = x . 3x
Câu 27: Viết dạng lũy thừa với số mũ hữu tỉ của biểu thức 2 3
a . a ( a > 0 ). Kết quả đúng là 6 1 7 7 A. 7 a . B. 6 a . C. 6 a . D. 3 a .
Câu 28: Trong bốn hình dưới đây, có bao nhiêu hình là khối đa diện ? A. 3. B. 1. C. 4. D. 2. Trang 3/6 - Mã đề 268
Câu 29: Khối chóp tứ giác S.ABCD có đáy ABCD là hình vuông cạnh a, SA = a 2 là đường cao. Thể
tích V của khối chóp là 3 a 2 3 a 2 3 a 2 A. V = . B. V = . C. 3 V = a 2. D. V = . 2 3 6
Câu 30: Trong các hàm số sau, hàm số nào đồng biến trên tập ¡ . A. 3
y = -x +3x + 2. B. 3
y = x + 3x . C. 3
y = -x -3x + 2. D. 3
y = -x + 3x .
Câu 31: Cho hàm số y = f (x) liên tục trên đoạn [ 1 - 6; ]
13 và có đồ thị như hình bên dưới.
Gọi M và m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số đã cho trên đoạn [ 1 - 6; ]
13 . Tính M + m ta được. A. -5 . B. -2 . C. -4 . D. 11 - .
Câu 32: Phương trình 16x 5.4x -
+ 4 = 0 có hai nghiệm a,b , tổng a +b bằng : A. 1. B. 0. C. 5. D. 4. Câu 33: Cho hàm số 2 sin ( ) 5 x f x =
. Đạo hàm của hàm số f (x) là A. 2 sin 5 .xln 5.sin 2 . x B. 2 sin 5 .xln 5. C. 2 sin 5 .xln 5.2sin . x D. 2 sin 5 .xln 5.2 cos . x
Câu 34: Biết khối đa diện đều loại {3;4} có độ dài cạnh bằng 12 3 cm . Tính diện tích toàn phần của
khối đa diện đều đó. A. 2 2592 cm . B. 2 1728cm . C. 2 864 3 cm . D. 2 648 3 cm .
Câu 35: Cho hình lăng trụ ABC.A’B’C’ có đáy là tam giác vuông cân ở C. Cạnh BB’ = a và tạo với
đáy một góc bằng 600. Hình chiếu vuông góc hạ từ B’ lên đáy trùng với trọng tâm của tam giác ABC.
Thể tích khối lăng trụ ABC.A’B’C’ là 3 a A. 3 3a 3 . B. 9 3a 3 . C. 3a 3 9 . D. . 80 80 80 80 x + 3
Câu 36: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là 2 4 - x - 9x + 9 A. 1. B. 2. C. 3. D. 4.
Câu 37: Giá trị của m để đồ thị hàm số 4 2
f (x)  x  8x  3 cắt đường thẳng y  3m tại 4 điểm phân biệt khi
A. 9 < m < 39. B. 13 - < m < 1.
C. 3 < m <13 . D. 1 - 3 < m < 3. 3 Câu 38: Cho hàm số 4 2
y = x - (m +1)x + 2m +1 có đồ thị (C ) đi qua điểm M (1,3) m
Giá trị của m là A. m =1 . B. m = 2 - . C. m = 2 . D. m = 0. Trang 4/6 - Mã đề 268
Câu 39: Cho hình chóp tam giác S.ABCD có đáy là hình vuông cạnh 6a . Tam giác SAB đều và
nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp
S.ABCD theo a. A. 3 V = 26p a 21 . B. 3 V = 28p a 21 . C. 3 V = 30p a 21 . D. 3 V = 24p a 21 .
Câu 40: Tìm tập xác định D của hàm số y = log x + log (x + 4) . 2 2
A. D = é-2 + 6;+¥ ë
). B. D =( 2-+ 5;+¥). C. D =( 2-+ 6;+¥). D. D = é-2+ 5;+¥ ë ). Câu 41: Hàm số 2 3
y = (x + 2019) (x - 2020) có bao nhiêu điểm cực trị ? A. 4. B. 3. C. 2. D. 1. x
Câu 42: Tìm tất cả giá trị thực của m để hàm số y = sin x -
+ 2019 nghịch biến trên toàn trục số. m A. m > 0 .
B. m ³ 1 hoặc m < 0 . C. m £ 1.
D. 0 < m £ 1 .
Câu 43: Tìm tất cả cá giá trị của m để phương trình 2 log
x - 8 log x - 8m + 4 = 0 vô nghiệm trên 2 2 đoạn [1;4] .
A. m < 0 hoặc 1 m > . B. 1 0 < m < 2 2 C. m < 0 .
D. m £ 0 hoặc 1 m ³ . 2
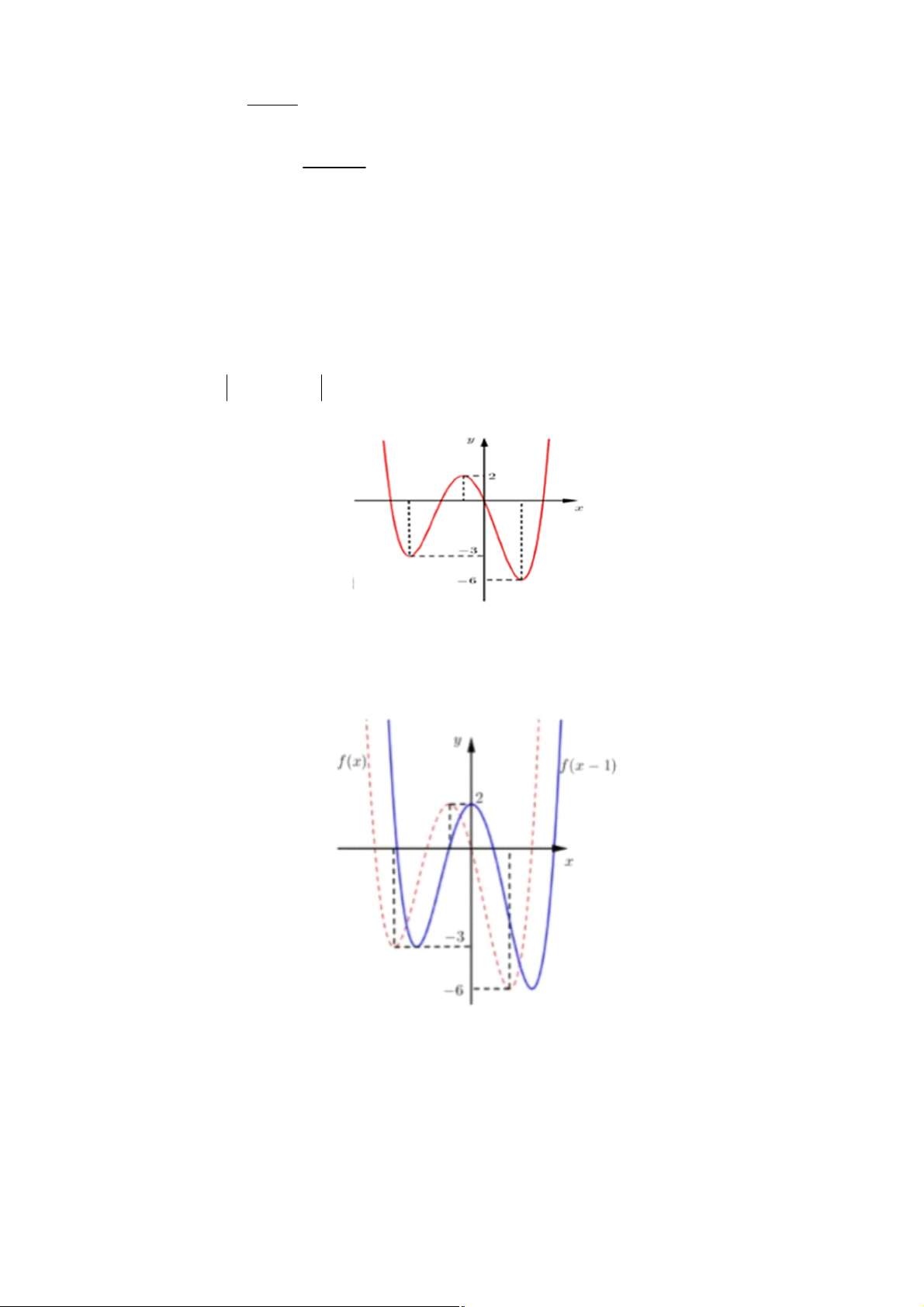
Câu 44: Hình vẽ bên là đồ thị của hàm số y = f (x). Gọi S là tập hợp các số nguyên dương của tham
số m để hàm số y = f (x - )
1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng: A. 9. B. 18. C. 15. D. 12.
Câu 45: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a . Biết hình chiếu vuông góc
của đỉnh S lên mặt phẳng đáy là điểm M trung điểm cạnh AD và tam giác SMB cân. Tính thể tích V
của khối chóp S.MBCD . 3 4a 5 3 a 5 A. 3 V = a 5 . B. V = . C. 3 V = a 3 . D. V = . 3 3
Câu 46: Bác nông dân T bán lúa và một đàn lợn thu được 120 triệu đồng. Bác T dự định gửi tiết
kiệm toàn bộ số tiền này vào ngân hàng với lãi suất 0,9% / tháng. Hỏi sau hai năm mới rút toàn bộ
tiền gốc và tiền lãi cho con đi học, khi đó bác T thu được bao nhiêu ? (giả sử lãi suất không đổi và
kết quả làm tròn đến 3 chữ số thập phân theo đơn vị triệu đồng)
A. 148,788 triệu đồng.
B. 122,169 triệu đồng.
C. 148,789 triệu đồng.
D. 122,170 triệu đồng. Trang 5/6 - Mã đề 268
Câu 47: Một trang trại trồng rau sạch theo tiêu chuẩn VietGap tại địa điểm B để cung cấp cho siêu
thị A đặt trên hòn đảo cách xa đất liền 160km (đoạn AH trên hình vẽ). Người ta dự định xây một
trạm tàu tại vị trí C để vận chuyển rau xanh ra đảo. Biết rằng tốc độ vận chuyển của xe chở trên đất
liền là 70km/h và của tàu hàng trên biển là 40km/h. Hỏi phải chọn điểm C cách B bao xa để thời
gian vận chuyển rau xanh ra đảo là ít nhất, biết khoảng cách từ trang trại B đến siêu thị A trên đảo là
300km. (kết quả làm tròn đến 2 chữ số thập phân) A. 142,36 km. B. 142,34 km. C. 142,40 km. D. 142,38 km.
Câu 48: Một hình nón có góc ở đỉnh bằng 0
60 và đường kính đường tròn đáy bằng 8a . Mặt phẳng
(a ) đi qua đỉnh của hình nón và cách tâm đường tròn đáy 2a . Tính diện tích S thiết diện của mặt
phẳng (a ) cắt hình nón đã cho. 2 48a 2 2 192a 2 2 384a 2 2 96a 2 A. S = . B. S = . C. S = . D. S = . 11 11 11 11
Câu 49: Có bao nhiêu giá trị nguyên của tham số a Î[-2019;2019] để hàm số 4 2 2 3
y = x - 2ax - a + a
tiếp xúc với trục hoành tại hai điểm phân biệt. A. 2020. B. 3. C. 2. D. 1.
Câu 50: Cho hàm số y f x có bảng biên thiên như hình vẽ Hàm số æ ö g ( x) 5 3 2
= f 2x - x - ç
÷ nghịch biến trên khoảng è 2 2 ø A. æ 5 ö æ ö æ ö æ ö 1; . ç ÷ B. 1 1 - ; . ç ÷ C. 9 ; +¥ . ç ÷ D. 1 ;1 . ç ÷ è 4 ø è 4 ø è 4 ø è 4 ø ----------- HẾT ----------
Học sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm
Họ và tên học sinh:................................................................. Số báo danh:............................ Trang 6/6 - Mã đề 268 TRƯỜNG THPT LONG THẠNH
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2019 – 2020 TỔ: TOÁN MÔN THI: TOÁN 12
Thời gian làm bài: 90 phút (không kể thời gian giao đề) (Đề có 06 trang) Ngày thi: 14/12/2019 Mã đề 182
Câu 1: Cho hàm số y = f (x) có bảng biến sau, chọn khẳng định đúng.
A. Hàm số nghịch biến trên khoảng (2; +¥) .
B. Hàm số nghịch biến trên khoảng (0; 2) .
C. Hàm số đồng biến trên khoảng (0; 2) .
D. Hàm số đồng biến trên khoảng ( ; -¥ 2) .
Câu 2: Tìm tập xác định D của hàm số y = log x - 5 . 3,14 ( ) A. D = ( ;5 -¥ ). B. D = ( ;5 -¥ ] .
C. D = [5;+¥) .
D. D = (5;+¥) .
Câu 3: Giải phương trình 10x = 2019 ta được nghiệm
A. x = log 2019 . B. 10 x = 2019 . C. 2019 x = .
D. x = ln 2019 . 10
Câu 4: Trong những công thức dưới đây, công thức sai là:
A. log 1 = a,(a > 0,a ¹ 1).
B. log a = 1,(a > 0,a ¹ 1). a a
C. log 1 = 0, (a > 0,a ¹ 1).
D. log aa = a,(a > 0, a ¹ 1). a a
Câu 5: Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất: A. Bốn mặt. B. Hai mặt. C. Ba mặt. D. Năm mặt.
Câu 6: Công thức tính thể tích khối lăng trụ có diện tích đáy là B và chiều cao h là : 1 1 1
A. V = Bh . B. V = . Bh C. V = . Bh D. V = . Bh 3 2 6
Câu 7: Cho hàm số y = f (x) có đồ thị như hình bên dưới.
Hỏi đường thẳng y = 2 cắt đồ thị hàm số đã cho tại bao nhiêu điểm ? A. 1. B. 2. C. 4. D. 3.
Câu 8: Công thức tính diện tích xung quanh của hình nón có bán kính đáy r và đường sinh l là
A. S = 2p rl . B. 2
S = 2p rl + 2p r . C. 2
S = p rl + p r .
D. S = p rl . xq xq xq xq x + 5
Câu 9: Đường tiệm cận đứng của đồ thị hàm số y = là x - 4 A. x = 4 - . B. x = 4 . C. x = 5 - . D. x = 5. Trang 1/6 - Mã đề 182
Câu 10: Tìm giá trị lớn nhất của hàm số 8
f (x) = +1 trên đoạn [4;2019] . x A. 1 2027
max f (x) = - . B. max f (x) = 5.
C. max f (x) = .
D. max f (x) = 3. [4;2019] 2 [4;2019] [4;2019] 2019 [4;2019]
Câu 11: Cho hàm số y = f (x) có đồ thị như hình bên. y -1 x O 1 - 1
Số cực trị của hàm số là: A. 1. B. 3. C. 0 . D. 2 .
Câu 12: Hình bát diện đều là khối đa diện đều loại A. {4 } ;3 . B. {5 } ;3 . C. {3 } ;4 . D. {3 } ;3 .
Câu 13: Mặt cầu có bán kính là R thì có diện tích là : A. 2 S = 4p R . B. 2 S = p R . C. 3 S = 4p R . D. 2 S = 2p R .
Câu 14: Công thức tính thể tích khối chóp có diện tích đáy là B và chiều cao h là : A. 1 V = . Bh B. 1 V = . Bh C. V = . Bh D. 1 V = . Bh 2 3 6
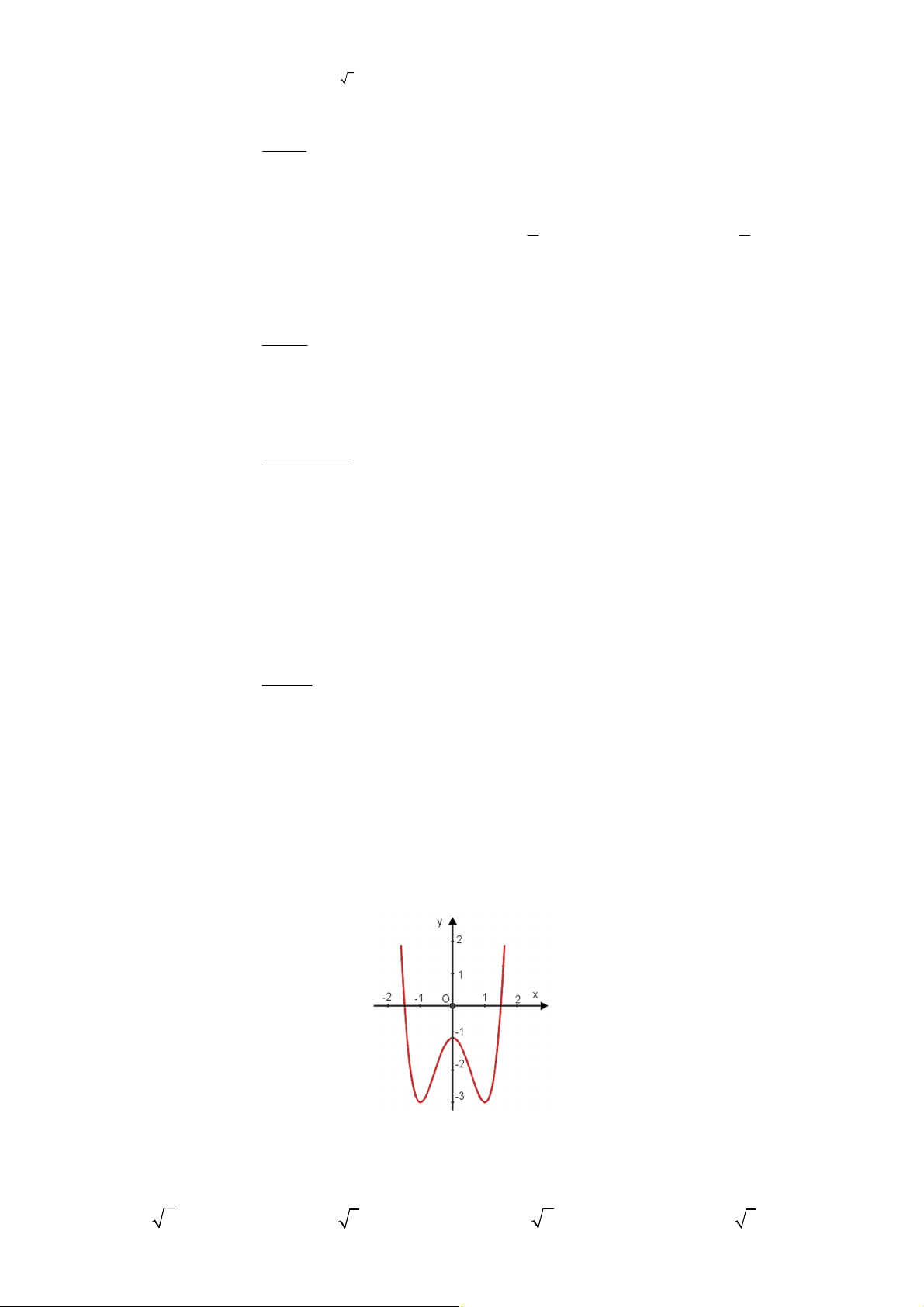
Câu 15: Đồ thị bên dưới là của một trong bốn hàm số y = f (x) được liệt kê ở bốn phương án. Hãy
chọn khẳng định đúng. A. 3 2
y = -2x - 4x - 3 . B. 3 2
y = 2x - 4x + 3 . C. 3 2
y = -2x - 4x + 3 . D. 3 2
y = 2x - 4x - 3.
Câu 16: Bất phương trình x
a > b , (b > 0) có nghiệm là :
A. x > log b a Î ¡
B. x < log b a > a với . a với 1.
C. x > log b a > x > b < a < a với 1. D. loga với 0 1.
Câu 17: Cho hàm số y xa =
. Khẳng định sai là:
A. Tập xác định của hàm số là D = ¡ khi a Î ¡ .
B. Tập xác định của hàm số là D = ¡ khi a là số nguyên dương.
C. Tập xác định của hàm số là D = ¡ \{ }
0 khi a là số nguyên âm.
D. Tập xác định của hàm số là D = (0; +¥) khi a Î ¤
Câu 18: Với a là số thực dương và a, b Î ¡ . Chọn khẳng định sai. a A. b
aa .ab = aa+b . B. ( a ) a . a a b = .
C. a = aa-b . D. a b a . a .a a b = . ab Trang 2/6 - Mã đề 182
Câu 19: Bất phương trình log (x +1) > 2 3 có nghiệm là: A. x >10 B. x > 5. C. x > 8. D. x < 8.
Câu 20: Cho khối chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Về phía ngoài khối chóp
này ta ghép thêm một khối tứ diện đều có cạnh bằng a, sao cho một mặt của khối tứ diện đều trùng
với một mặt bên của khối chóp đã cho. Số mặt của khối đa diện mới lập thành là A. 5. B. 8. C. 7. D. 6. Câu 21: Hàm số 4
y = 2020 - x nghịch biến trên khoảng nào ? A. ( 20 - 20;+¥) . B. ( ; -¥ 2020) . C. ( ;0 -¥ ). D. (0;+¥). 3 Câu 22: Thu gọn 3 2 4
p . p . p ta được 23 32 12 32 A. 12 p . B. 12 p . C. 23 p . D. 21 p .
Câu 23: Mặt cầu ngoại tiếp một hình lập phương cạnh a thì có thể tích là: 3 3 3a p 3p 3 3a p 3 3a p A. 27a V = . B. V = . C. V = . D. V = . 4 4 2 6
Câu 24: Tìm điều kiện của x để hàm số y = log (x - 2) xác định. 3 A. x < 2. B. x ¹ 2. C. x Î . ¡ D. x > 2.
Câu 25: Tính đạo hàm của hàm số y = ( x - )52 2 3 . 5 2
A. y = ( x - )23 ' 5 2 3 .
B. y ' = (2x - 3)32 .
C. y = ( x - )32 ' 5 2 3 .
D. y ' = (2x - 3)32 . 2 5
Câu 26: Phương trình log (x - 3) = 1 - 1 có nghiệm là: 2 A. x = 3. B. x = 5. C. x = 2 . D. x = 1.
Câu 27: Hình trụ có chu vi đáy là 8p và chiều cao h = 6 . Diện tích xung quanh của hình trụ là
A. S = 12p.
B. S = 24p.
C. S = 36p.
D. S = 48p. xq xq xq xq +
Câu 28: Đường hypebol (H) là đồ thị của hàm số ax b y =
(xem hình vẽ). Hỏi đó là hàm số nào ? cx + d - + + + A. x 3 x x x y = . B. 2 3 y = . C. 3 y = . D. 3 y = . x +1 x +1 x -1 x +1
Câu 29: Cho khối tứ diện ABCD có diện tích B D CD bằng 2 32a và thể tích 3
V = 216a . Tính khoảng
cách h từ điểm A đến mặt phẳng (BCD) . A. a a a h = 27a . B. 27 h = . C. 9 h = . D. 81 h = . 4 4 4 Trang 3/6 - Mã đề 182
Câu 30: Thu gọn biểu thức P = log log 256a , (0 < a ¹ 1) ta được a 4
A. P = 2(1+ log 2) .
B. P = 2(1+ 2 log 2) .
C. P = 2(1- log 2) .
D. P = 2(1- 2log 2) . a a a a + Câu 31: Cho hàm số 2x 1 y =
. Giá trị lớn nhất M, giá trị nhỏ nhất m của hàm số trên đoạn [2;4] x -1 lần lượt là
A. M = 5; m = 3 .
B. M = 4; m = 9 . C. 9 M = ; m = -3. D. 2 M = - ; m = -2. 2 9
Câu 32: Cho phương trình x 1+ 2 3
- 3 -x = 15 . Đặt = 3x t
(t > 0) ta nhận được phương trình nào ? A. 2
3t + 9t -15 = 0 . B. 2
t - 5t - 3 = 0 . C. 2
t - 5t + 3 = 0 . D. 2
t + 5t - 3 = 0 . 2x - 3
Câu 33: Cho hàm số y =
có đồ thị (H ) và đường thẳng (d ) có phương trình y = x + 2 . Gọi m x + 4
là số giao điểm của đường thẳng (d ) và (H ) . Chọn khẳng định đúng. A. m = 2 . B. m = 1. C. m = 3 . D. m = 0. x - 2
Câu 34: Cho hàm số y =
với m là tham số. Đồ thị hàm số đã cho không có tiệm cận đứng 2 x - mx +1 khi A. m < 2 - hoặc m > 2 . B. m = 2 - . C. 2   m  2. D. m = 2 . Câu 35: Cho hàm số 3
y = x - 3x . Đồ thị hàm số có hai điểm cực đại và cực tiểu,với giá tri cực đại, giá
trị cực tiểu lần lượt là a và b . Khẳng định đúng là: A. . a b = 1 -
B. a - b = 0 .
C. a + b = 0. D. . a b = 4 + Câu 36: Cho hàm số mx 4 y =
. Chọn khẳng định đúng. x + m
A. Hàm số đồng biến trên từng khoảng xác định khi 2 - < m < 2 .
B. Hàm số nghịch biến trên từng khoảng xác định khi 2 - < m < 2 .
C. Hàm số đồng biến trên từng khoảng xác định khi m > 2 - .
D. Hàm số nghịch biến trên từng khoảng xác định khi m < 2 - hoặc m > 2 .
Câu 37: Bất phương trình 2
log x - 9.log x -10 > 0 có tập nghiệm là (0;a) và (b; +¥) . Tính . a b . 2 2 A. . a b = 512. B. . a b = 0. C. . a b = 1024. D. . a b = 2048.
Câu 38: Cho đồ thị hàm số 4 2
y = ax + bx + c như hình vẽ bên dưới. Chọn khẳng định sai. A. ac < 0 . B. c < 0 . C. ab > 0 . D. ab < 0 .
Câu 39: Cho hình chóp S.ABCD , ABCD là hình vuông cạnh a , SA vuông góc với đáy, góc giữa SC và đáy là 0
60 . Bán kính mặt cầu ngoại tiếp hình chóp đã cho có độ dài là
A. R = 2a 2. B. R = 2a 3.
C. R = a 2.
D. R = a 3. Trang 4/6 - Mã đề 182
Câu 40: Hình tứ diện diện đều ABCD cạnh a có chiều cao là: a 6 a 3 a 3 a 6 A. . B. . C. . D. . 6 3 6 3
Câu 41: Cho hình chóp tam giác S.ABC có thể tích 3
V = 324 cm . Gọi M, N lần lượt là trung điểm
của cạnh SA, SB. Tính thể tích V của khối đa diện ABCMN . A. 3 V = 243 cm . B. 3 V = 126 cm . C. 3 V = 81 cm . D. 3 V = 162 cm .
Câu 42: Tính đạo hàm của hàm số y = ( 2
ln 5 + 3x - x ) ta được - + - A. 2x 3 2x 1 3 2x y ' = . B. y ' = . C. y ' = . D. y ' = . 2 5 + 3x - x 2 5 + 3x - x 2 5 + 3x - x 2 5 + 3x - x
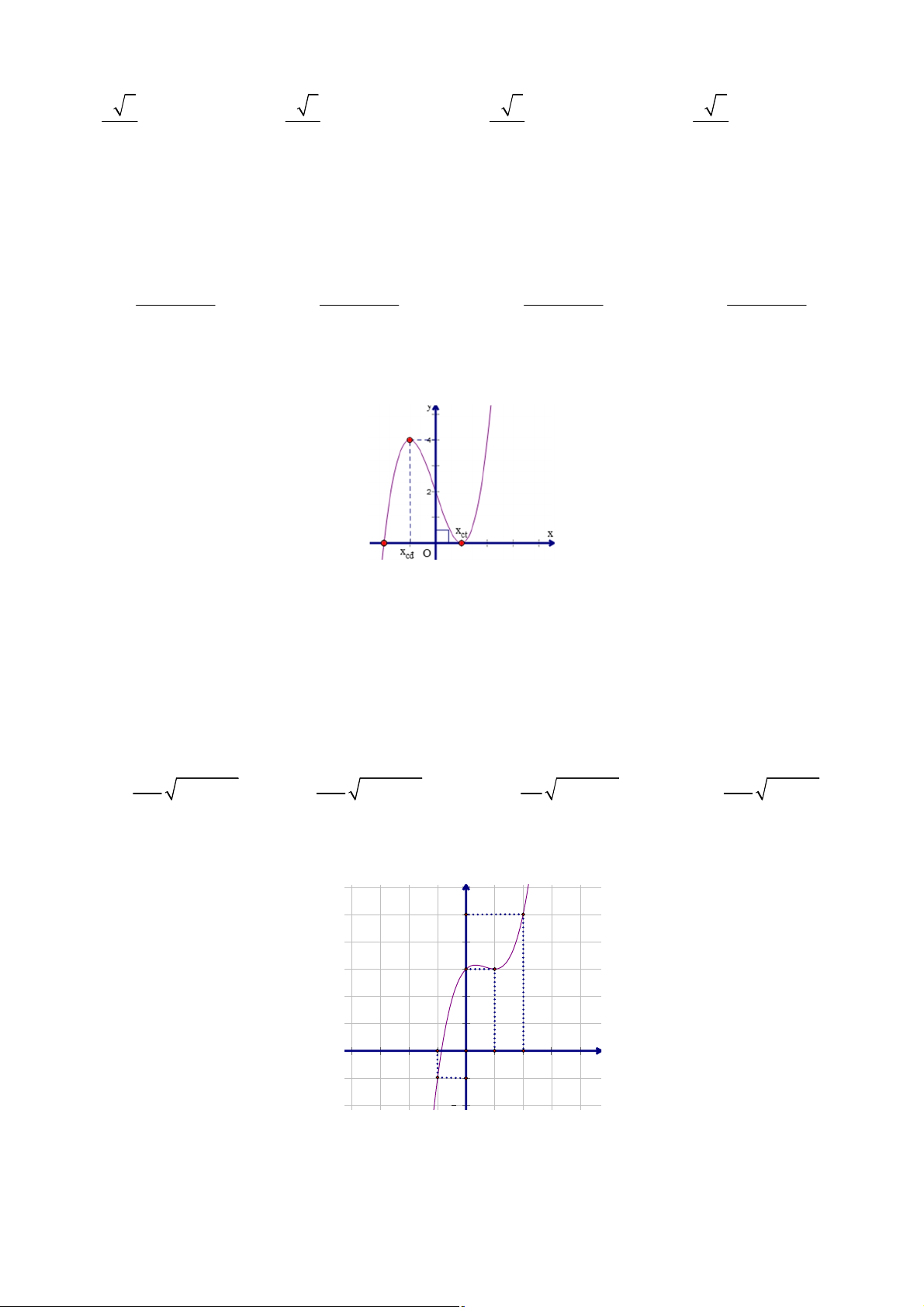
Câu 43: Cho hàm số y = f ( x) có đồ thị như hình bên. Có bao nhiêu giá trị nguyên của m để
phương trình f ( x) = m có ba nghiệm phân biệt trong đó có hai nghiệm âm và một nghiệm dương? A. 2. B. 0. C. 1. D. 3. Câu 44: Cho hàm số 3 2 2
f (x) = x + ax - (1+ b )x - 5(a + b) . Hỏi có bao nhiêu giá trị nguyên của tham số
a và b để hàm số đã cho luôn có hai điểm cực trị. A. 5. B. Vô số. C. 0. D. 2019.
Câu 45: Cho hình chóp S.ABCD , ABCD là hình thang cân, đáy lớn AB bằng 4 lần đáy nhỏ CD
chiều cao của đáy bằng a . Bốn đường cao của bốn mặt bên ứng với đỉnh S bằng nhau và bằng b . Thể tích hình chóp là 2 5a 2 5a 2 a 2 5a A. 2 2 V =
b - 4a . B. 2 2 V = 4b - a . C. 2 2 V = 4b - a . D. 2 2 V = b - a . 24 24 24 8
Câu 46: Cho hàm số y = f (x) có đạo hàm và liên tục trên ¡ . Biết rằng đồ thị hàm số /
y = f ( x) như dưới đây. 6 y 5 4 3 2 -1 x O 1 2 -1 2
Giá trị lớn nhất max g (x) của hàm số ( ) = ( ) 2 g x
f x - x - x trên đoạn [ 1 - ; 2] là: [-1;2]
A. max g ( x) = g (0). B. max g ( x) = g (2).
C. max g (x) = g ( ) 1 .
D. max g ( x) = g (- ) 1 . [ 1 - ;2] [ 1 - ;2] [-1;2] [ 1 - ;2] Trang 5/6 - Mã đề 182
Câu 47: Cho hàm số đa thức y = f (x) xác định và liên tục trên ¡ có đồ thị f ('x) như hình bên dưới.
Hỏi hàm số y = f (5 - x) đồng biến trên khoảng nào được liệt kê dưới đây ? A. ( ) ;1 -¥ . B. (3;8) . C. ( ;5 -¥ ) . D. (5;+¥) .
Câu 48: Cường độ ánh sáng đi qua một môi trường khác không khí, chẳng hạn như nước, sương
mù, ...sẽ giảm dần tùy theo độ dày của môi trường và một hằng số m gọi là khả năng hấp thu tùy
thuộc môi trường theo công thức như sau: - x
I = I e m với x là độ dày của môi trường đó, tính bằng 0
mét. Biết rằng nước biển có m = 1, 4 . Hãy tính xem cường độ ánh sáng giảm đi bao nhiêu lần từ độ
sâu 2 mét xuống đến 20 mét ? A. 10 7, 7947.10 lần. B. 10 8, 7947.10 lần. C. 10 lần. D. 10 6, 7947.10 lần. 2y +1
Câu 49: Cho hai số thực không âm x, y thỏa mãn 2
x + 2x - y +1 = log
. Tìm giá trị nhỏ nhất 2 x +1 m của 2 x 1 - 2 P = e + 4x - 2y +1. 1 A. m = - . B. m = e- 3. C. m = 1. - D. m = e. 2
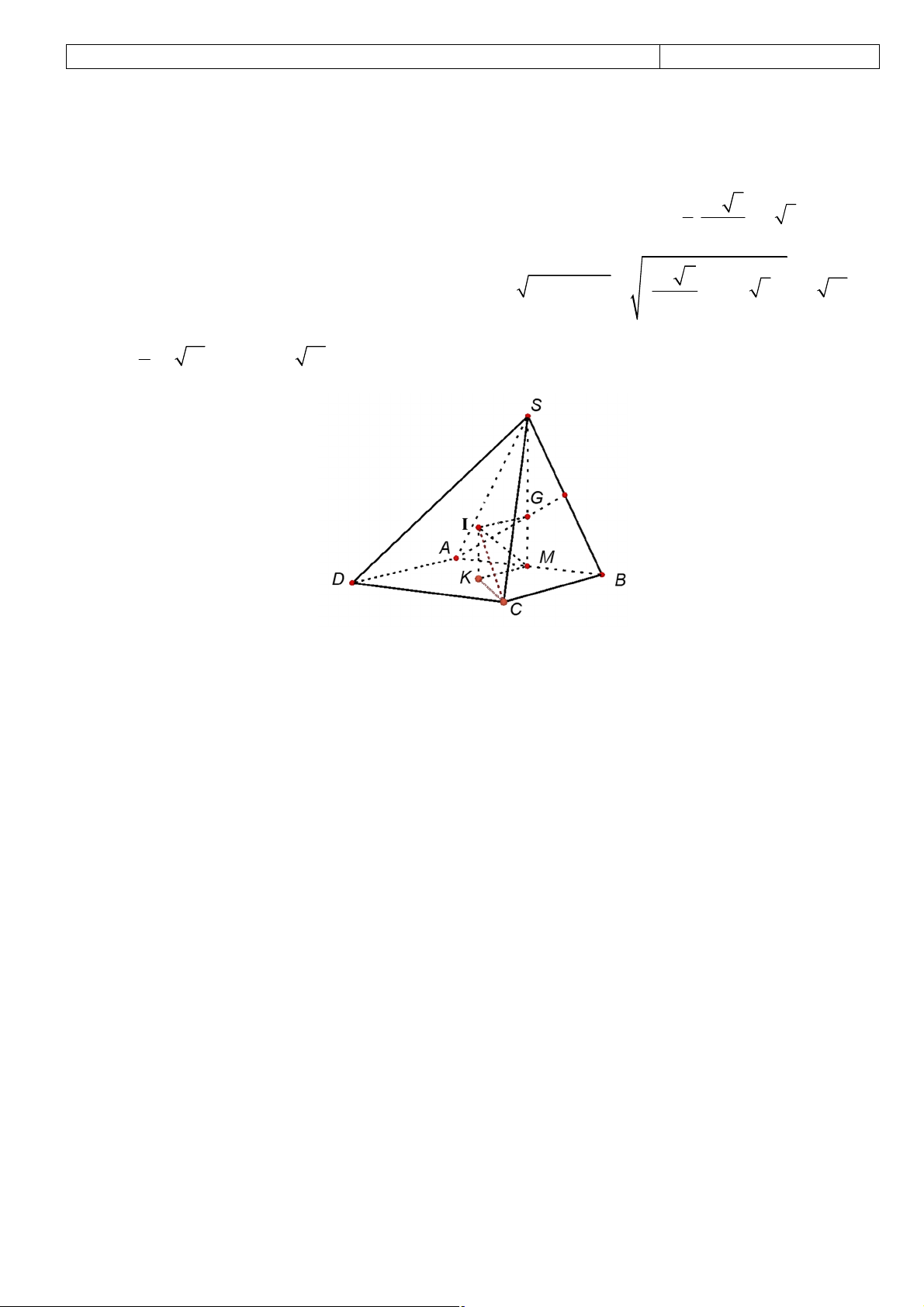
Câu 50: Cho mặt cầu có đường kính AB = 2R . Trên AB lấy I sao cho AI = h (0 < h < 2R) , một mặt
phẳng vuông góc với AB tại I cắt mặt cầu theo đường tròn (C) . Xác định vị trí của I để thể tích
khối nón đỉnh A , đáy là đường tròn (C) đạt giá trị lớn nhất thì độ dài AI là 5R A. 2R R R AI = . B. AI = . C. AI = . D. 4 AI = . 3 3 3 3 ----------- HẾT ----------
Học sinh không được sử dụng tài liệu, giám thị không giải thích gì thêm
Họ và tên học sinh:................................................................. Số báo danh:............................ Trang 6/6 - Mã đề 182
SỞ GD&ĐT KIÊN GIANG
THI HỌC KỲ I – NĂM HỌC 2019 - 2020 TRƯỜNG THPT LONG THẠNH
MÔN TOÁN - KHỐI LỚP 12
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm: 182 268 386 475 Ghi chú 1 B A D C 2 D C D C 3 A A B B 4 A D B D 5 C D D D 6 A C C B 7 D B A B 8 D B B A 9 B A A D 10 D C C D 11 B C A D 12 C B C A 13 A C D D 14 B A C B 15 B C C D 16 C D C C 17 A B D C 18 D D A B 19 C D C B 20 A D D D 21 D D A A 22 A D D B 23 C D D A 24 D B D D 25 C D B C 26 B A C C 27 D C A A 28 D B A A 29 D B D C 30 B B A D 31 A C D C 32 B A B A 33 D A C C 34 C C C A 35 C B A B 36 B C C D 37 A B D D 38 C C B A 39 C B B A 40 D D B A 41 A C D B 42 D D A B 43 C A D D 44 B D A C 45 B A B B 46 C A C C 47 A A A A 48 B B B C 49 A D B D 50 D A B B 1
Hướng dẫn giải một số câu Vận dụng – Vận dụng cao + Câu: Cho hàm số mx 4 y =
. Chọn khẳng định đúng. x + m 2 m - 4
Hướng dẫn giải: Ta có: ' ' 2 y =
; y < 0 Û m - 4 < 0 Û 2 - < m < 2 2 (x + m) Câu: Cho hàm số 3
y = x -3x . Đồ thị hàm số có hai điểm cực đại và cực tiểu,với giá tri cực đại, giá
trị cực tiểu lần lượt là a và b . Khẳng định đúng là:
Hướng dẫn giải: Ta có: ' 2
y = 3x - 3 = 0 Û x = 1
± . Hàm số đạt cực đại tại x = 1
- , đạt giá trị cực đại
y = 2 , đạt cực tiểu tại y = -2 . Vậy a = 2;b = 2
- nên a + b = 0 .
Câu : Hình vẽ bên là đồ thị của hàm số y = f (x). Gọi S là tập hợp các số nguyên dương của tham
số m để hàm số y = f (x - )
1 + m có 5 điểm cực trị. Tổng giá trị tất cả các phần tử của S bằng:
Hướng dẫn giải: Đồ thị hàm số y = f (x - )
1 nhận được bằng cách tịnh tiến đồ thị hàm số y = f ( x)
sang phải 1 đơn vị nên không làm thay đổi tung độ các điểm cực trị.
Đồ thị hàm số y = f (x - )
1 + m nhận được bằng cách tịnh tiến đồ thị hàm số y = f ( x - ) 1 lên trên m đơn vị nên ta có: y = 2 + ; m y = 3 - + , m y = 6 CD CT CT - + m 1
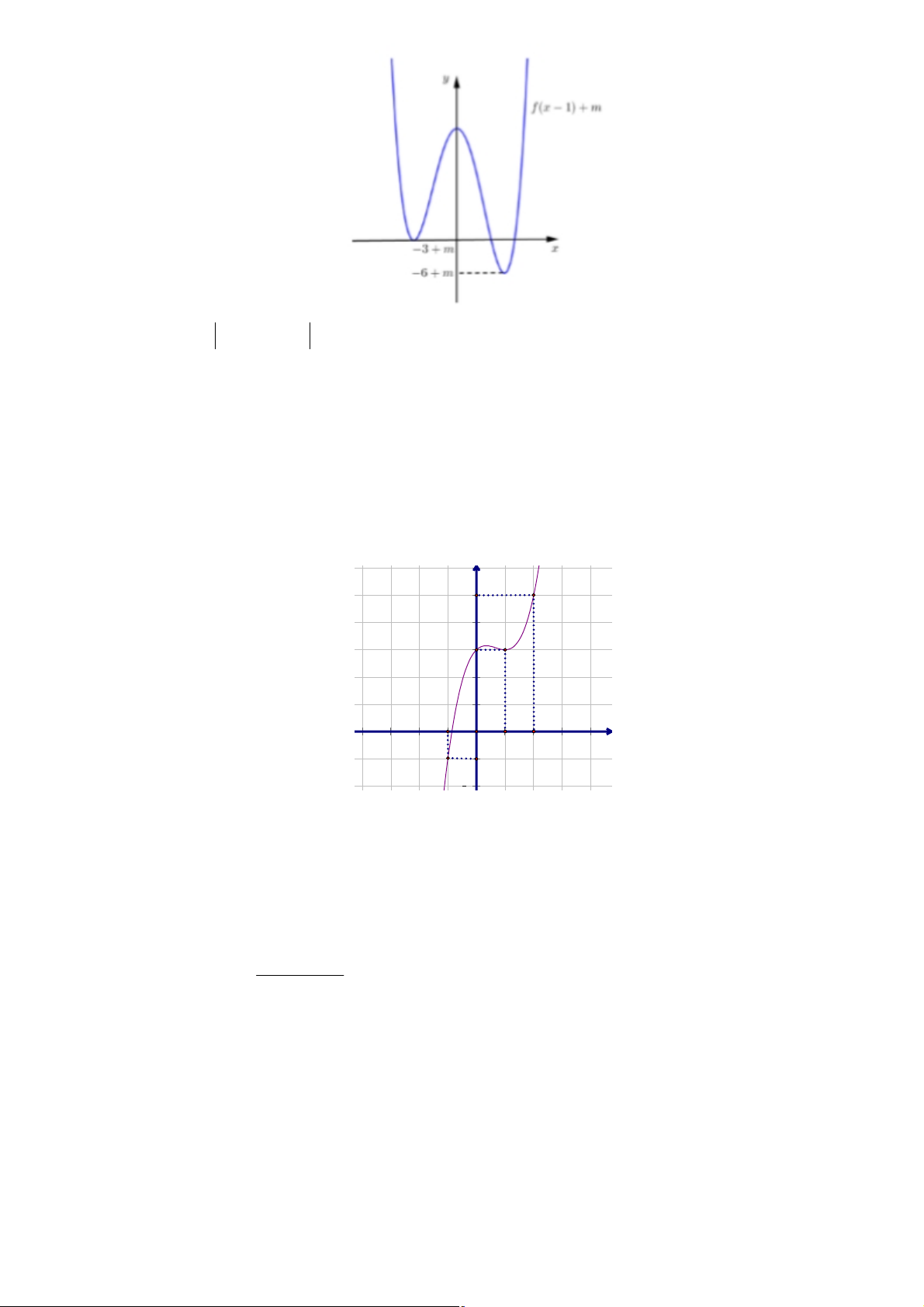
Đồ thị hàm số y = f (x - )
1 + m nhận được bằng cách từ đồ thị hàm số y = f\left( x-1 \right)+m lấy đối
xứng phần đồ thị phía dưới trục hoành qua trục hoành và xóa đi phần đồ thị phía dưới trục hoành.
Để đồ thị hàm số có 5 cực trị
Û -6 + m < 0 £ -3+ m Û 3 £ m < 6 Þ m Î{3;4 } ;5 Þ S = {3;4; } 5 Þ 3 + 4 + 5 = 12.
Câu: Cho hàm số y = f ( x) có đạo hàm và liên tục trên ¡ . Biết rằng đồ thị hàm số /
y = f ( x) như dưới đây. 6 y 5 4 3 2 -1 x O 1 2 -1 2
Giá trị lớn nhất max g ( x) của hàm số ( ) = ( ) 2 g x
f x - x - x trên đoạn [ 1 - ; 2]là: [ 1 - ;2]
Hướng dẫn giải: ( ) = ( ) 2 g x
f x - x - x nên ' ' '
g (x) = f (x) - 2x -1 = 0 Û f (x) = 2x +1 Û x =1; x = 2. Xét dấu '
g (x) < 0 trên đoạn [1;2]vậy max g ( x) = g ( ) 1 . [ 1 - ;2] x - 2
Câu : Cho hàm số y =
với m là tham số. Đồ thị hàm số đã cho không có tiệm cận đứng 2 x - mx +1 khi
Hướng dẫn giải: Đồ thị hàm số không có tiêm cận đứng khi 2
x - mx +1 = 0 vô nghiệm, tức 2
m - 4 < 0 Û -2 < m < 2 .
Câu : Cho hàm số y f x có bảng biên thiên như hình vẽ 2  
Hàm số gx 5 3 2  f 2x   x   
nghịch biến trên khoảng:  2 2
Hướng dẫn giải: æ 5 ö æ 5 3 ö Ta có g¢( x) 2 = 4x -
f ¢ 2x - x - . ç ÷ ç ÷ è 2 ø è 2 2 ø é 5 x = 5 ê é 8 4x - = 0 ê ê 2 5 3 ê ì 1 5 9 ü Xét g¢( x) 2 = 0 Û ê
Û 2x - x - = -2 Û x Î í 1 - ; ; ;1; ý. ê æ 5 3 ö ê 2 2 2 î 4 8 4
f ¢ 2x - x - = 0 þ ç ÷ ê êë è 2 2 ø 5 3 2 ê 2x - x - = 3 êë 2 2 Bảng biến thiên
Dựa vào bảng biến thiên, ta chọn  5 1  ;   .  (So sánh các đáp án)  4 2y +1
Câu: Cho hai số thực không âm thỏa mãn 2
x + 2x - y +1 = log
. Tìm giá trị nhỏ nhất m của 2 x +1 2x 1 - 2 P = e + 4x - 2y +1.
Hướng dẫn giải: Ta biến đổi PT về dạng hàm đặc trưng: 2y +1 1 2 2
x + 2x - y +1 = log
Û x + 2x - y +1 = log (2y +1) - log (x+1) 2 2 2 x +1 2 2
Û 2 x + 4x + 2log (x +1) = log (2y +1) + 2y 2 2 2 2
Û 2(x +1) + log 2(x +1) = log (2y +1) + 2y +1 2 2 1 '
f (t) = log t + t,t > 0. f (t) = +1 > 0 2 t.ln 2
Hàm f (t) đồng biến trên (0;+¥) . 2 2 2x 1 - 2 2
f (2(x+1) ) = f (2y +1) Û 2(x+1) = 2y +1 Û P = e
+ 4x - 2(x +1) + 2
Tìm GTNN của P ta được kết quả 1 p ³ - 2
Câu : Tìm tất cả cá giá trị của m để phương trình 2
log x - 8log x - 8m + 4 = 0 vô nghiệm trên đoạn 2 2 [1;4]
Hướng dẫn giải: Ta có 2 2
log x - 8log x - 8m + 4 = 0 Û 4 log x - 8log x = 8m - 4 2 2 2 2 3 2
Û log x - 2log x = 2m -1 . Đặt t = log x , x Î 1;4 Þ t Î 0;2 . 2 [ ] [ ] 2 2 Ta có 2
f (t) = t - 2t thì max f (t) = 0 , min f (t) = -1 . [0;2] [0;2] é 1 é2m -1 > 0 m >
Do đó để phương trình 2
t - 2t = 2m -1 vô nghiệm trên [0;2] thì ê Û ê 2 ë2m -1 < -1 ê ëm < 0
Câu: Cho hình chóp S.ABCD , ABCD là hình thang cân, đáy lớn AB bằng 4 lần đáy nhỏ CD chiều
cao của đáy bằng a . Bốn đường cao của bốn mặt bên ứng với đỉnh S bằng nhau và bằng b . Thể tích hình chóp là
Hướng dẫn giải: (Tự vẽ hình nhe !)
H là chân đường cao của hình chóp thì H cách đều các cạnh của đáy, H nằm trong đáy. Suy ra đáy
có đường tròn nội tiếp tâm H là trung điểm MN với M, N lần lượt là trung điểm AB và CD, MN = a.
Đường tròn tiếp xúc BC tại E thì HM = HN = HE = a là bán kính đường tròn, ta có SE = SM = SN 2 = b ( a 1 b > 2 ) suy ra 2 2 SH =
4b - a . Đặt CN = x, BM = 4x, CE = x, BE= 4x. Tam giác HBC vuông 2 2 2 a a a 5a 2 5a ở H nên 2
= 4x Þ x = Þ CD = , AB = 2a Þ S = . Ta có kết quả 2 2 V = 4b - a . 4 4 2 ABCD 4 24
Câu: Cho mặt cầu có đường kính AB = 2R . Trên AB lấy I sao cho AI = h (0 < h < 2R) , một mặt
phẳng vuông góc với AB tại I cắt mặt cầu theo đường tròn (C) . Xác định vị trí của I để thể tích
khối nón đỉnh A , đáy là đường tròn (C) đạt giá trị lớn nhất thì độ dài AI là
Hướng dẫn giải: (tự vẽ hình nhe) Goi EF là đường kính của ( C). Ta có: 2 IE = I .
A IB = h(2R - h) .
Bán kính của (C) r = IE = h(2R - h) . 2 1 p h
Thể tích hình nón đỉnh A là 2 V = p r h =
(2R - h) (0 < h < 2R) 3 3 p 4R 4R ' 2 V =
(4Rh - 3h ) = 0 Û h = Þ V Û h = = IA max 3 3 3 x
Câu: Tìm tất cả giá trị thực của m để hàm số y = sin x -
+ 2019 nghịch biến trên toàn trục số. m 1
Hướng dẫn giải: Ta có y ' = cos x -
. Để hàm số nghịch biến trên toàn trục số thì y ' £ 0 x " Î ¡ m 1 Û 1 cos x - £ 0 x
" Ρ . Mà | cos x |£1 x
" Î ¡, từ đó suy ra ³1 Û 0 < m £1. m m Câu: Hàm số 2 3
y = (x + 2019) (x - 2020) có bao nhiêu điểm cực trị ?
Hướng dẫn giải: Ta có 3 2 2
y ' = 2(x + 2019)(x - 2020) + 3(x + 2019) (x - 2020) 2
y ' = (x + 2019)(x - 2020) .[2(x - 2020) + 3(x + 2019)].
Suy ra phương trình y ' = 0 có 2 nghiệm phân biệt và một nghiệm kép.
Vậy hàm số đã cho có 2 điểm cực trị. 4 Câu: Cho hàm số 3 2 2
f (x) = x + ax - (1+ b )x - 5(a + )
b . Hỏi có bao nhiêu giá trị nguyên của tham số a
và b để hàm số đã cho luôn có hai điểm cực trị.
Hướng dẫn giải: Ta có 2 2
f '(x) = 3x + 2ax - (1+ b ) . Ta thấy 2 3.é-(1+ b )ù < 0 b " Î ë û ¡ .
Do đó phương trình y ' = 0 luôn có 2 nghiệm phân biệt.
Vậy có vô số giá trị nguyên của a và b thỏa yêu cầu bài toán.
Câu: Một trang trại trồng rau sạch theo tiêu chuẩn VietGap tại địa điểm B để cung cấp cho siêu thị
A đặt trên hòn đảo cách xa đất liền 160km (đoạn AH trên hình vẽ). Người ta dự định xây một trạm
tàu tại vị trí C để vận chuyển rau xanh ra đảo. Biết rằng tốc độ vận chuyển của xe chở trên đất liền là
70km/h và của tàu hàng trên biển là 40km/h. Hỏi phải chọn điểm C cách B bao xa để thời gian vận
chuyển rau xanh ra đảo là ít nhất, biết khoảng cách từ trang trại B đến siêu thị A trên đảo là 300km.
(kết quả làm tròn đến 2 chữ số thập phân)
Hướng dẫn giải: Ta có 2 2
HB = 300 -160 = 20 161 .
Đặt BC = x (km) Þ x Î(0;20 161) và HC = 20 161 - x Đoạn AC = + ( - x)2 2 160 20 161 + ( - x x )2 2 160 20 161
Tổng thời gian vận chuyển là t(x) = + 70 40
Tìm min của hàm số t(x) trên (0;20 161), ta được t » 6,91h khi x »142,36 km . min x + 3
Câu: Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số y = là 2 -4x - 9x + 9 x + 3 1
Hướng dẫn giải: Ta viết lại y = = (x + 3)(3 - 4x) x + 3.(3 - 4x) æ 3 ö æ 3 Ta có tập xác định ö D = 3; È ; +¥ ç ÷ ç ÷ . è 4 ø è 4 ø 3
Từ đó ta thấy hàm số có 2 tiệm cận đứng là x = -3, x = và 1 tiệm cận ngang y = 0. 4
Vậy tổng cộng có 3 đường tiệm cận. 5
Câu: Cho đồ thị hàm số 4 2
y = ax + bx + c như hình vẽ bên dưới. Chọn khẳng định sai.
Hướng dẫn giải: Ta thấy đồ thị hàm số có 3 điểm cực trị. éx = 0 Do đó phương trình 3 2 y ' 4ax
2bx 2x(2ax b) 0 ê = + = + = Û
- có 3 nghiệm phân biệt. 2 b êx = ë 2a -b Suy ra > 0 Û ab < 0 . 2a
Câu: Cho hàm số đa thức y = f (x) xác định và liên tục trên ¡ có đồ thị f ('x) như hình bên dưới.
Hỏi hàm số y = f (5 - x) đồng biến trên khoảng nào được liệt kê dưới đây ?
Hướng dẫn giải: Từ đồ thị ta suy ra f '(x) = ax(x + 3)(x - 2) (a < 0) .
Mà đề cho y = f (5 - x) , suy ra [ f (5- x)]' = - f '(5- x) = (-a)(5- x)(8- x)(3- x) = 0
Phương trình này có 3 nghiệm là 3; 5; 8 và hệ số (-a)( 1 - )( 1 - )( 1 - ) < 0 .
Lập bảng biến thiên, suy hàm số y = f (5 - x) đồng biến trên ( ; -¥ 3) và (5;8) .
Vậy chọn hàm số đồng biến trên khoảng ( ; -¥ 1) .
Câu: Có bao nhiêu giá trị nguyên của tham số a Î[-2019;2019] để hàm số 4 2 2 3
y = x - 2ax - a + a tiếp
xúc với trục hoành tại hai điểm phân biệt.
Hướng dẫn giải: Từ đề bài ta tính được 3 2
y ' = 4x - 4ax = 4x(x - a) .
Hàm số đã cho là hàm bậc 4 nên muốn tiếp xúc với trục hoành tại 2 điểm thì hàm số phải có 3 cực
trị. Hay phương trình y ' = 0 có 3 nghiệm phân biệt. éx = 0 Ta có y ' = 0 Û ê
. Do đó a > 0 và 3 điểm cực trị là x = 0, x = ± a . 2 ëx = a 6 éa = 0
Hàm số tiếp xúc với trục hoành nên 3 2
y( a) = 0 Û a - 2a = 0 Û ê . ëa = 2
Vậy a = 2 (vì a > 0 )
Câu: Cường độ ánh sáng đi qua một môi trường khác không khí, chẳng hạn như nước, sương mù,
...sẽ giảm dần tùy theo độ dày của môi trường và một hằng số m gọi là khả năng hấp thu tùy thuộc
môi trường theo công thức như sau: - x
I = I e m với x là độ dày của môi trường đó, tính bằng mét. 0
Biết rằng nước biển có m = 1, 4 . Hãy tính xem cường độ ánh sáng giảm đi bao nhiêu lần từ độ sâu 2 mét xuống đến 20 mét ?
Hướng dẫn giải: Từ công thức đề cho - x
I = I e m lần lượt áp dụng tại độ sâu 2 mét và 20 mét ta có: 0 -m 2 - 2 I I e I = I e m ; - 20
I = I e m . Suy ra tỉ số 2 0 18 = = e m 2 0 20 0 -m20 I I e 20 0 I
Với nước biển ta có m = 1, 4 , tính được tỉ số 2 10 » 8,7947.10 lần. I20
(Từ đó ta nhận thấy, khi xuống sâu 20 mét thì gần như không có ánh sáng dưới biển)
Câu: Cho hình chóp tứ giác S.ABCD có đáy là hình vuông cạnh 2a . Biết hình chiếu vuông góc của
đỉnh S lên mặt phẳng đáy là điểm M trung điểm cạnh AD và tam giác SMB cân. Tính thể tích V của
khối chóp S.MBCD .
Hướng dẫn giải: Vì tam giác SMB vuông tại M nên chỉ có thể cân tại đỉnh M.
Do đó chiều cao hình chóp 2 2
SM = MB = (2a) + a = a 5 1
1 æ (2a + a).2a Thể tích khối chóp ö S.MBCD là 3 V = S .SM = .a 5 = a 5 ç ÷ 3 MBCD 3 è 2 ø
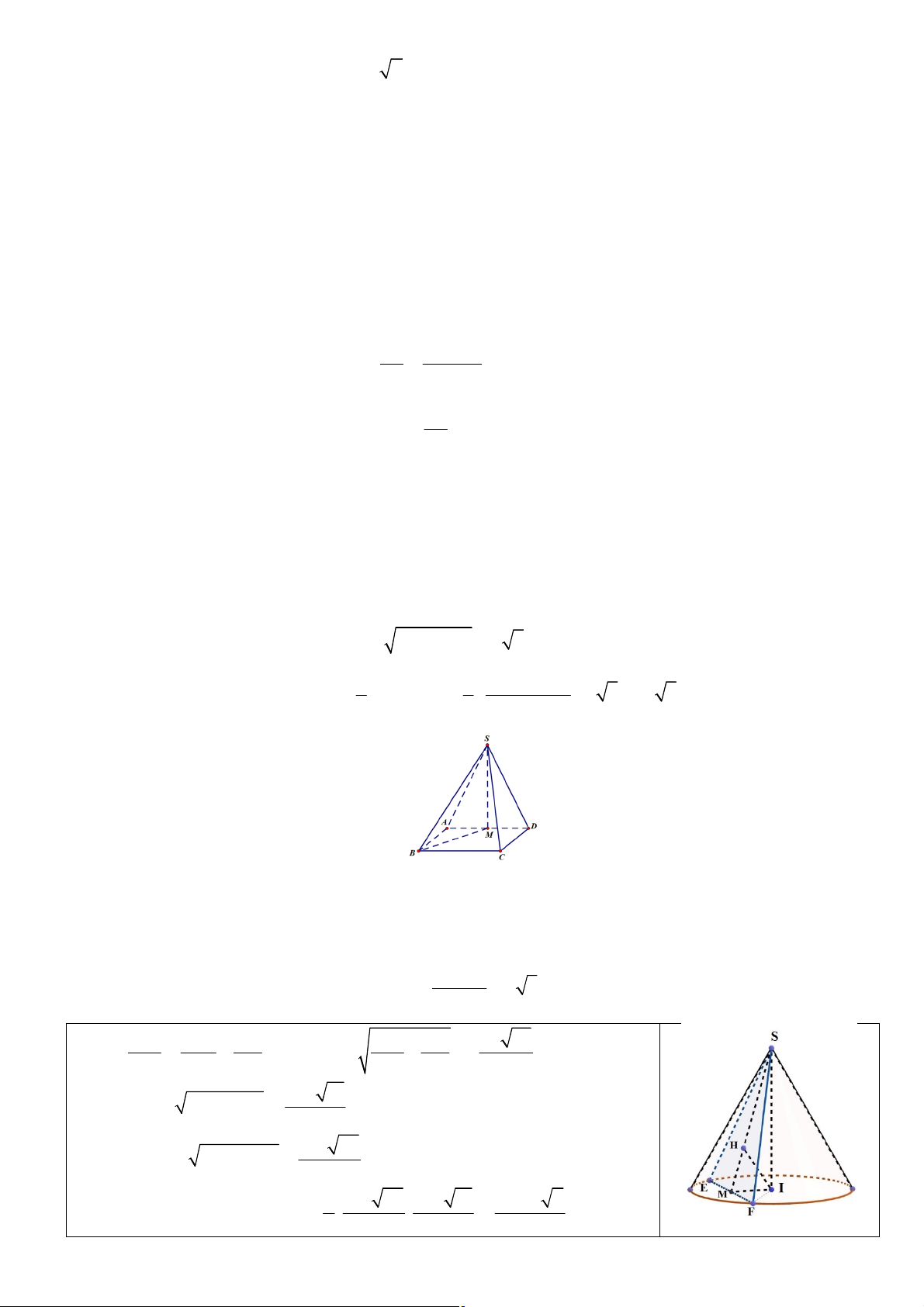
Câu: Một hình nón có góc ở đỉnh bằng 0
60 và đường kính đường tròn đáy bằng 8a . Mặt phẳng (a )
đi qua đỉnh của hình nón và cách tâm đường tròn đáy 2a . Tính diện tích S thiết diện của mặt phẳng
(a ) cắt hình nón đã cho.
Hướng dẫn giải: Chiều cao hình nón là 4a SI = = 4 3a . 0 tan 30 1 1 1 1 1 4a 33 Ta có = + Þ IM =1: - = 2 2 2 2 2 IH IM SI IH SI 11 24a 11 Ta có 2 2
SM = IM + SI = 11 16a 22 2 2
EF = 2MF = 2 IF - IM = 11 2 1 16a 22 24a 11 192a 2
Vậy diện tích thiết diện S = . . = SEF 2 11 11 11 7
Câu: Cho hình chóp tam giác S.ABCD có đáy là hình vuông cạnh 6a . Tam giác SAB đều và nằm
trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối cầu ngoại tiếp hình chóp S.ABCD theo a. 1 6a 3
Hướng dẫn giải: G là trọng tâm tam giác SAB, M là trung điểm AB, GM = . = a 3 3 2 2 æ ö 2 6a 2
K là tâm mặt đáy, bán kính mặt cầu ngoại tiếp 2 2
R = IC = KC + KI = ç ÷ + ç ÷ (a 3) = a 21 2 è ø Vậy 4
V = p ( 21a)3 3 = 28p a 21 3 8
Document Outline

  • De 268.docx
  • De 182.docx
  • Dap_an_4_ma_de.docx
  • Huong dan giai.docx