Đề thi học kì 1 Toán 12 năm 2019 – 2020 trường TH Thực hành Sài Gòn – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi học kỳ 1 môn Giới Toán 12 năm học 2019 – 2021 .Mời bạn đọc đón xem.

24 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 12

Môn: Toán 12

Thông tin:

18 trang 8 tháng trước

Tác giả:

Profile Lan Tường
Trang 1/4 - Mã đề thi 101
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
(Đề thi có 04 trang)
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 – 2020
MÔN: TOÁN – LỚP: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Mã đề thi 101
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
A.
1;2
max 15
y
. B.
1;2
max 6
y
C.
1;2
max 11
y
. D.
1;2
max 10
y
.
Câu 2: Tính tổng các nghiệm của phương trình
2 3 2 3 14
x x
.
A.
2
B.
4
C.
0
D.
2
Câu 3: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
A.
3
2 2
3
a
. B.
3
2 3
3
a
. C.
3
2 2
a
. D.
3
2
a
.
Câu 4: Tìm tập xác định của hàm số
2
ln 3 2
y x x
.
A.
;1 2;
. B.
1;2
.
C.
;1 2;
.. D.
1;2
.
Câu 5: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
A.
3
CT
y
. B.
4
CT
y
. C.
4
CT
y
. D.
3
CT
y
.
Câu 6: Cho hàm số
y f x
liên tục trên đoạn
0;4
có đồ thị như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
0
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực đại tại
4
x
. D. Hàm số đạt cực đại tại
2
x
.
Câu 7: Tính đạo hàm của hàm số
2
2
log 2
f x x x
.
A.
2
ln 2
2
f x
x x
. B.
2
1
2 ln2
f x
x x
.
-2
4
3
2
y
x
1
O
Đ
Ề CHÍNH THỨC
Trang 2/4 - Mã đề thi 101
C.
2
2 2 ln2
2
x
f x
x x
. D.
2
2 2
2 ln2
x
f x
x x
.
Câu 8: Viết phương trình tiếp tuyến với đồ thị hàm số
1
1
x
y
x
biết tiếp tuyến song song với
đường thẳng
: 2 1 0
x y
.
A.
2 7
y x
B.
2 7
y x
C.
2 1
y x
D.
2
y x
Câu 9: Cho hàm số
y f x
liên trục trên
và có đạo hàm
2 2017
' 1 2 3 .
f x x x x
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số nghịch biến trên khoảng
1;3
.
C. Hàm số đồng biến trên các khoảng
1;2
và
3;

.
D. Hàm số đạt cực đại tại
2
x
, đạt cực tiểu tại
1
x
và
3
x
.
Câu 10: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
4 2
4 2
y x x
B.
4 2
4 2
y x x
C.
4 2
4 2
y x x
D.
4 2
4 2
y x x
Câu 11: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích
xung quanh của hình nón đó.
A.
2
3
a
B.
2
2
a
C.
2
4
a
D.
2
2
a
Câu 12: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập
?
A.
2
log 1 .
y x
B.
2
2
log 1 .
y x
C.
1
.
2
x
y
D.
2
log 2 1 .
x
y
Câu 13: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
A.
5 2
.
2
r
B.
5 2
.
2
r
C.
5 .
r
D.
5.
r
Câu 14: Giải bất phương trình sau
1 1
5 5
log 3 5 log 1
x x
.
A.
5
3
3
x
B.
5
1
3
x
. C.
3
x
. D.
1 3
x
.
Câu 15: Tìm số đường tiệm cận của đồ thị hàm số
2
2
3 2
.
4
x x
y
x
A.
1
B.
2
C.
0
D.
3
Trang 3/4 - Mã đề thi 101
Câu 16: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
A.
1 2
m
. B.
2
m
. C.
2
m
. D.
2 3
m
.
Câu 17: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
3
mặt phẳng. B.
4
mặt phẳng. C.
6
mặt phẳng. D.
9
mặt phẳng.
Câu 18: Cho hàm số
3
.
2
x
y
x
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
\ 2
.
B. Hàm số nghịch biến trên mỗi khoảng
( ;2)
và
(2; ).
C. Hàm số nghịch biến trên mỗi khoảng
( ; 2)
và
( 2; ).
D. Hàm số đồng biến trên khoảng
( ; 2) ( 2; ).
Câu 19: Tìm tập nghiệm của bất phương trình
5 1
2 4
x
.
A.
1
;
5

. B.
1
;
5

. C.
1
;
5

. D.
1
;
5

.
Câu 20: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
A.
2
. B.
6 4 2
. C.
4
. D.
2
log 6 4 2
.
Câu 21: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
6
. B.
13
. C.
3
. D.
4
.
Câu 22: Cho mặt cầu bán kính
R
ngoại tiếp một hình lập phương cạnh
.
a
Mệnh đề nào dưới đây
là đúng?
A.
2 2
a R
. B.
3
R
a
. C.
2
a R
. D.
2
3
R
a
.
Câu 23: Cho
49
log 11
a
;
2
log 7
b
. Tính
3
7
121
log
8
theo
,
a b
.
A.
3
7
121 9
log 3
8
a
b
. B.
3
7
121
log 12 9
8
a b
C.
3
7
121 9
log 12
8
a
b
D.
3
7
121 1 3
log
8 3
a b
.
Câu 24: Cho hình chóp
.
S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với
mặt phẳng đáy và
2
SA a
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
5
3
a
. B.
5
5
a
. C.
2 2
3
a
. D.
2 5
5
a
.
Câu 25: Tìm số nghiệm của phương trình
2
2 2
log 2 log 3 4
x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 26: Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
,
AB AC a
120
BAC
. Mặt phẳng
( )
AB C
tạo với đáy một góc
60
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
8
a
V
. D.
3
3
4
a
V
.
Trang 4/4 - Mã đề thi 101
Câu 27: Cho hàm số
4 2
f x ax bx c
với
0
a
,
2019
c
và
2019
a b c
. Tìm
số điểm cực trị của đồ thị hàm số
2019
y f x
.
A.
1
. B.
7
. C.
3
. D.
5
.
Câu 28: Một người vay ngân hàng
200
triệu đồng với lãi suất là
0,6%
một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng
9
triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới
9
triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
A.
22
. B.
23
. C.
24
. D.
25
.
Câu 29: Cho lăng trụ
. ' ' '
ABC A B C
có đáy
ABC
là tam giác đều cạnh có độ dài bằng
2.
Hình
chiếu vuông góc của
'
A
lên mặt phẳng
ABC
trùng với trung điểm
H
của
.
BC
Góc tạo bởi
cạnh bên
'
AA
với mặt đáy là
0
45 .
Tính thể tích khối trụ đã cho.
A.
1.
V
B.
3.
V
C.
6
.
24
V
D.
6
.
8
V
Câu 30: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
3
2
0
1 ,
t
Q t Q e
với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau
bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1
t h
B.
1,2
t h
C.
1, 34
t h
D.
1, 54
t h
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
Câu 32: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
Câu 33: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
Câu 34: Giải bất phương trình
1 1
5 5
log 3 5 log 1
x x
.
Câu 35: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh
bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
Câu 37: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích
xung quanh của hình nón đó.
----------- HẾT ----------
Trang 1/4 - Mã đề thi 102
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
(Đề thi có 04 trang)
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 – 2020
MÔN: TOÁN – LỚP: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Mã đề thi 102
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Cho hàm số
y f x
liên tục trên đoạn
0;4
có đồ thị như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại
0
x
. B. Hàm số đạt cực đại tại
2
x
.
C. Hàm số đạt cực đại tại
4
x
. D. Hàm số đạt cực tiểu tại
3
x
.
Câu 2: Giải bất phương trình sau
1 1
5 5
log 3 5 log 1
x x
.
A.
5
3
3
x
B.
5
1
3
x
. C.
3
x
. D.
1 3
x
.
Câu 3: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
4 2
4 2
y x x
B.
4 2
4 2
y x x
C.
4 2
4 2
y x x
D.
4 2
4 2
y x x
Câu 4: Tìm tập nghiệm của bất phương trình
5 1
2 4
x
.
A.
1
;
5

. B.
1
;
5

. C.
1
;
5

. D.
1
;
5

.
Câu 5: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập
?
A.
2
2
log 1 .
y x
B.
2
log 2 1 .
x
y
-2
4
3
2
y
x
1
O
Đ
Ề CHÍNH THỨC
Trang 2/4 - Mã đề thi 102
C.
1
.
2
x
y
D.
2
log 1 .
y x
Câu 6: Tìm số đường tiệm cận của đồ thị hàm số
2
2
3 2
.
4
x x
y
x
A.
1
B.
2
C.
0
D.
3
Câu 7: Viết phương trình tiếp tuyến với đồ thị hàm số
1
1
x
y
x
biết tiếp tuyến song song với
đường thẳng
: 2 1 0
x y
.
A.
2 1
y x
B.
2
y x
C.
2 7
y x
D.
2 7
y x
Câu 8: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
A.
3
2 2
a
. B.
3
2 3
3
a
. C.
3
2 2
3
a
. D.
3
2
a
.
Câu 9: Tính tổng các nghiệm của phương trình
2 3 2 3 14
x x
.
A.
2
B.
2
C.
4
D.
0
Câu 10: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích xung
quanh của hình nón đó.
A.
2
3
a
B.
2
2
a
C.
2
4
a
D.
2
2
a
Câu 11: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
A.
1;2
max 11
y
. B.
1;2
max 15
y
. C.
1;2
max 10
y
. D.
1;2
max 6
y
Câu 12: Tính đạo hàm của hàm số
2
2
log 2
f x x x
.
A.
2
2 2
2 ln 2
x
f x
x x
. B.
2
2 2 ln 2
2
x
f x
x x
.
C.
2
ln 2
2
f x
x x
. D.
2
1
2 ln2
f x
x x
.
Câu 13: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
3
mặt phẳng. B.
4
mặt phẳng. C.
6
mặt phẳng. D.
9
mặt phẳng.
Câu 14: Tìm tập xác định của hàm số
2
ln 3 2
y x x
.
A.
;1 2;

.. B.
1;2
.
C.
1;2
. D.
;1 2;
.
Câu 15: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
A.
1 2
m
. B.
2
m
. C.
2
m
. D.
2 3
m
.
Câu 16: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
A.
3
CT
y
. B.
3
CT
y
. C.
4
CT
y
. D.
4
CT
y
.
Câu 17: Cho hàm số
3
.
2
x
y
x
Khẳng định nào sau đây là đúng?
Trang 3/4 - Mã đề thi 102
A. Hàm số đồng biến trên
\ 2
.
B. Hàm số nghịch biến trên mỗi khoảng
( ;2)
và
(2; ).
C. Hàm số nghịch biến trên mỗi khoảng
( ; 2)
và
( 2; ).

D. Hàm số đồng biến trên khoảng
( ; 2) ( 2; ).
Câu 18: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
A.
2
. B.
6 4 2
. C.
4
. D.
2
log 6 4 2
.
Câu 19: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
A.
5 2
.
2
r
B.
5 2
.
2
r
C.
5 .
r
D.
5.
r
Câu 20: Cho hàm số
y f x
liên trục trên
và có đạo hàm
2 2017
' 1 2 3 .
f x x x x
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng
1;2
và
3;

.
C. Hàm số nghịch biến trên khoảng
1; 3
.
D. Hàm số đạt cực đại tại
2
x
, đạt cực tiểu tại
1
x
và
3
x
.
Câu 21: Cho
49
log 11
a
;
2
log 7
b
. Tính
3
7
121
log
8
theo
,
a b
.
A.
3
7
121 9
log 3
8
a
b
. B.
3
7
121
log 12 9
8
a b
C.
3
7
121 9
log 12
8
a
b
D.
3
7
121 1 3
log
8 3
a b
.
Câu 22: Cho hình chóp
.
S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với
mặt phẳng đáy và
2
SA a
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
2 5
5
a
. B.
5
5
a
. C.
2 2
3
a
. D.
5
3
a
.
Câu 23: Cho mặt cầu bán kính
R
ngoại tiếp một hình lập phương cạnh
.
a
Mệnh đề nào dưới đây
là đúng?
A.
2
a R
. B.
2 2
a R
. C.
3
R
a
. D.
2
3
R
a
.
Câu 24: Tìm số nghiệm của phương trình
2
2 2
log 2 log 3 4
x x .
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 25: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
3
. B.
6
. C.
13
. D.
4
.
Câu 26: Một người vay ngân hàng
200
triệu đồng với lãi suất là
0,6%
một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng
9
triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới
9
triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
A.
22
. B.
23
. C.
24
. D.
25
.
Trang 4/4 - Mã đề thi 102
Câu 27: Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
,
AB AC a
120
BAC
. Mặt phẳng
( )
AB C
tạo với đáy một góc
60
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
4
a
V
. B.
3
3
8
a
V
. C.
3
9
8
a
V
. D.
3
8
a
V
.
Câu 28: Cho lăng trụ
. ' ' '
ABC A B C
có đáy
ABC
là tam giác đều cạnh có độ dài bằng
2.
Hình
chiếu vuông góc của
'
A
lên mặt phẳng
ABC
trùng với trung điểm
H
của
.
BC
Góc tạo bởi
cạnh bên
'
AA
với mặt đáy là
0
45 .
Tính thể tích khối trụ đã cho.
A.
1.
V
B.
3.
V
C.
6
.
24
V
D.
6
.
8
V
Câu 29: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
3
2
0
1 ,
t
Q t Q e
với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau
bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1
t h
B.
1,2
t h
C.
1, 34
t h
D.
1, 54
t h
Câu 30: Cho hàm số
4 2
f x ax bx c
với
0
a
,
2019
c
và
2019
a b c
. Tìm
số điểm cực trị của đồ thị hàm số
2019
y f x
.
A.
7
. B.
5
. C.
1
. D.
3
.
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
Câu 32: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
Câu 33: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
Câu 34: Giải bất phương trình
1 1
5 5
log 3 5 log 1
x x
.
Câu 35: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh
bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
Câu 37: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích
xung quanh của hình nón đó.
----------- HẾT ----------
Trang 1/4 - Mã đề thi 104
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
(Đề thi có 04 trang)
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 – 2020
MÔN: TOÁN – LỚP: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Mã đề thi 103
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích xung
quanh của hình nón đó.
A.
2
2
a
B.
2
2
a
C.
2
4
a
D.
2
3
a
Câu 2: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
A.
3
2 2
a
. B.
3
2 3
3
a
. C.
3
2 2
3
a
. D.
3
2
a
.
Câu 3: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
A.
2
. B.
4
. C.
2
log 6 4 2
. D.
6 4 2
.
Câu 4: Tính tổng các nghiệm của phương trình
2 3 2 3 14
x x
.
A.
2
B.
2
C.
4
D.
0
Câu 5: Viết phương trình tiếp tuyến với đồ thị hàm số
1
1
x
y
x
biết tiếp tuyến song song với
đường thẳng
: 2 1 0
x y
.
A.
2 1
y x
B.
2
y x
C.
2 7
y x
D.
2 7
y x
Câu 6: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập
?
A.
2
log 2 1 .
x
y
B.
1
.
2
x
y
C.
2
2
log 1 .
y x
D.
2
log 1 .
y x
Câu 7: Tính đạo hàm của hàm số
2
2
log 2
f x x x
.
A.
2
1
2 ln2
f x
x x
. B.
2
2 2 ln 2
2
x
f x
x x
.
C.
2
ln 2
2
f x
x x
. D.
2
2 2
2 ln2
x
f x
x x
.
Câu 8: Cho hàm số
y f x
liên tục trên đoạn
0;4
có đồ thị như hình vẽ.
Đ
Ề CHÍNH THỨC
Trang 2/4 - Mã đề thi 104
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại
2
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực tiểu tại
0
x
. D. Hàm số đạt cực đại tại
4
x
.
Câu 9: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
A.
3
CT
y
. B.
3
CT
y
. C.
4
CT
y
. D.
4
CT
y
.
Câu 10: Tìm tập xác định của hàm số
2
ln 3 2
y x x
.
A.
;1 2;

.. B.
1;2
.
C.
1;2
. D.
;1 2;
.
Câu 11: Cho hàm số
y f x
liên trục trên
và có đạo hàm
2 2017
' 1 2 3 .
f x x x x
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng
1;2
và
3;

.
C. Hàm số nghịch biến trên khoảng
1; 3
.
D. Hàm số đạt cực đại tại
2
x
, đạt cực tiểu tại
1
x
và
3
x
.
Câu 12: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
A.
6
mặt phẳng. B.
3
mặt phẳng. C.
4
mặt phẳng. D.
9
mặt phẳng.
Câu 13: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
A.
1;2
max 11
y
. B.
1;2
max 10
y
. C.
1;2
max 6
y
D.
1;2
max 15
y
.
Câu 14: Giải bất phương trình sau
1 1
5 5
log 3 5 log 1
x x
.
A.
5
1
3
x
. B.
5
3
3
x
C.
3
x
. D.
1 3
x
.
Câu 15: Cho hàm số
3
.
2
x
y
x
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
\ 2
.
B. Hàm số nghịch biến trên mỗi khoảng
( ;2)
và
(2; ).
C. Hàm số nghịch biến trên mỗi khoảng
( ; 2)
và
( 2; ).
D. Hàm số đồng biến trên khoảng
( ; 2) ( 2; ).
Câu 16: Tìm số đường tiệm cận của đồ thị hàm số
2
2
3 2
.
4
x x
y
x
-2
4
3
2
y
x
1
O
Trang 3/4 - Mã đề thi 104
A.
3
B.
1
C.
0
D.
2
Câu 17: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
A.
5 2
.
2
r
B.
5 2
.
2
r
C.
5 .
r
D.
5.
r
Câu 18: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
4 2
4 2
y x x
B.
4 2
4 2
y x x
C.
4 2
4 2
y x x
D.
4 2
4 2
y x x
Câu 19: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
A.
1 2
m
. B.
2
m
. C.
2
m
. D.
2 3
m
.
Câu 20: Tìm tập nghiệm của bất phương trình
5 1
2 4
x
.
A.
1
;
5

. B.
1
;
5

. C.
1
;
5

. D.
1
;
5

.
Câu 21: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
3
. B.
6
. C.
13
. D.
4
.
Câu 22: Cho
49
log 11
a
;
2
log 7
b
. Tính
3
7
121
log
8
theo
,
a b
.
A.
3
7
121 9
log 3
8
a
b
. B.
3
7
121
log 12 9
8
a b
C.
3
7
121 1 3
log
8 3
a b
. D.
3
7
121 9
log 12
8
a
b
Câu 23: Tìm số nghiệm của phương trình
2
2 2
log 2 log 3 4
x x
.
A.
0
. B.
1
. C.
2
. D.
3
.
Câu 24: Cho hình chóp
.
S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với
mặt phẳng đáy và
2
SA a
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
2 5
5
a
. B.
5
3
a
. C.
2 2
3
a
. D.
5
5
a
.
Câu 25: Cho mặt cầu bán kính
R
ngoại tiếp một hình lập phương cạnh
.
a
Mệnh đề nào dưới đây
là đúng?
A.
3
R
a
. B.
2
a R
. C.
2
3
R
a
. D.
2 2
a R
.
Trang 4/4 - Mã đề thi 104
Câu 26: Một người vay ngân hàng
200
triệu đồng với lãi suất là
0,6%
một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng
9
triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới
9
triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
A.
23
. B.
25
. C.
24
. D.
22
.
Câu 27: Cho lăng trụ
. ' ' '
ABC A B C
có đáy
ABC
là tam giác đều cạnh có độ dài bằng
2.
Hình
chiếu vuông góc của
'
A
lên mặt phẳng
ABC
trùng với trung điểm
H
của
.
BC
Góc tạo bởi
cạnh bên
'
AA
với mặt đáy là
0
45 .
Tính thể tích khối trụ đã cho.
A.
1.
V
B.
3.
V
C.
6
.
24
V
D.
6
.
8
V
Câu 28: Cho hàm số
4 2
f x ax bx c
với
0
a
,
2019
c
và
2019
a b c
. Tìm
số điểm cực trị của đồ thị hàm số
2019
y f x
.
A.
7
. B.
5
. C.
1
. D.
3
.
Câu 29: Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
,
AB AC a
120
BAC
. Mặt phẳng
( )
AB C
tạo với đáy một góc
60
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
3
4
a
V
. D.
3
8
a
V
.
Câu 30: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
3
2
0
1 ,
t
Q t Q e
với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau
bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1, 54
t h
B.
1,2
t h
C.
1
t h
D.
1, 34
t h
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
Câu 32: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
Câu 33: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
Câu 34: Giải bất phương trình
1 1
5 5
log 3 5 log 1
x x
.
Câu 35: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh
bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
Câu 37: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích
xung quanh của hình nón đó.
----------- HẾT ----------
Trang 1/4 - Mã đề thi 104
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
(Đề thi có 04 trang)
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 – 2020
MÔN: TOÁN – LỚP: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
Mã đề thi 104
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Tìm số đường tiệm cận của đồ thị hàm số
2
2
3 2
.
4
x x
y
x
A.
1
B.
2
C.
0
D.
3
Câu 2: Tính tổng các nghiệm của phương trình
2 3 2 3 14
x x
.
A.
2
B.
2
C.
4
D.
0
Câu 3: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
A.
2
log 6 4 2
. B.
6 4 2
. C.
2
. D.
4
.
Câu 4: Cho hàm số
y f x
liên tục trên đoạn
0;4
có đồ thị như hình vẽ.
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại
2
x
. B. Hàm số đạt cực tiểu tại
3
x
.
C. Hàm số đạt cực tiểu tại
0
x
. D. Hàm số đạt cực đại tại
4
x
.
Câu 5: Tính đạo hàm của hàm số
2
2
log 2
f x x x
.
A.
2
ln 2
2
f x
x x
. B.
2
1
2 ln2
f x
x x
.
C.
2
2 2
2 ln2
x
f x
x x
. D.
2
2 2 ln2
2
x
f x
x x
.
Câu 6: Tìm tập xác định của hàm số
2
ln 3 2
y x x
.
A.
;1 2;
.. B.
1;2
.
C.
1;2
. D.
;1 2;
.
-2
4
3
2
y
x
1
O
Đ
Ề CHÍNH THỨC
Trang 2/4 - Mã đề thi 104
Câu 7: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
A.
1;2
max 11
y
. B.
1;2
max 10
y
. C.
1;2
max 6
y
D.
1;2
max 15
y
.
Câu 8: Đường cong trong hình bên là đồ thị của hàm số nào?
A.
4 2
4 2
y x x
B.
4 2
4 2
y x x
C.
4 2
4 2
y x x
D.
4 2
4 2
y x x
Câu 9: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập
?
A.
2
log 2 1 .
x
y
B.
2
log 1 .
y x
C.
1
.
2
x
y
D.
2
2
log 1 .
y x
Câu 10: Cho hàm số
y f x
liên trục trên
và có đạo hàm
2 2017
' 1 2 3 .
f x x x x
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng
1;2
và
3;

.
C. Hàm số nghịch biến trên khoảng
1; 3
.
D. Hàm số đạt cực đại tại
2
x
, đạt cực tiểu tại
1
x
và
3
x
.
Câu 11: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích xung
quanh của hình nón đó.
A.
2
2
a
B.
2
2
a
C.
2
4
a
D.
2
3
a
Câu 12: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
A.
4
CT
y
. B.
3
CT
y
. C.
4
CT
y
. D.
3
CT
y
.
Câu 13: Giải bất phương trình sau
1 1
5 5
log 3 5 log 1
x x
.
A.
5
1
3
x
. B.
5
3
3
x
C.
3
x
. D.
1 3
x
.
Câu 14: Cho hàm số
3
.
2
x
y
x
Khẳng định nào sau đây là đúng?
A. Hàm số đồng biến trên
\ 2
.
B. Hàm số nghịch biến trên mỗi khoảng
( ;2)
và
(2; ).
C. Hàm số nghịch biến trên mỗi khoảng
( ; 2)
và
( 2; ).
D. Hàm số đồng biến trên khoảng
( ; 2) ( 2; ).
Câu 15: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối
xứng?
Trang 3/4 - Mã đề thi 104
A.
6
mặt phẳng. B.
4
mặt phẳng. C.
3
mặt phẳng. D.
9
mặt phẳng.
Câu 16: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
A.
5 2
.
2
r
B.
5 2
.
2
r
C.
5 .
r
D.
5.
r
Câu 17: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh
bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
A.
3
2 2
3
a
. B.
3
2
a
. C.
3
2 3
3
a
. D.
3
2 2
a
.
Câu 18: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
A.
1 2
m
. B.
2
m
. C.
2
m
. D.
2 3
m
.
Câu 19: Viết phương trình tiếp tuyến với đồ thị hàm số
1
1
x
y
x
biết tiếp tuyến song song với
đường thẳng
: 2 1 0
x y
.
A.
2 7
y x
B.
2
y x
C.
2 7
y x
D.
2 1
y x
Câu 20: Tìm tập nghiệm của bất phương trình
5 1
2 4
x
.
A.
1
;
5

. B.
1
;
5

. C.
1
;
5

. D.
1
;
5

.
Câu 21: Tìm số nghiệm của phương trình
2
2 2
log 2 log 3 4
x x
.
A.
2
. B.
1
. C.
3
. D.
0
.
Câu 22: Cho
49
log 11
a
;
2
log 7
b
. Tính
3
7
121
log
8
theo
,
a b
.
A.
3
7
121 9
log 12
8
a
b
B.
3
7
121 1 3
log
8 3
a b
.
C.
3
7
log 12 9
8
a b
D.
3
7
121 9
log 3
8
a
b
.
Câu 23: Gọi
S
là tập hợp tất cả các giá trị nguyên của tham số
m
sao cho phương trình
1 2
16 .4 5 45 0
x x
m m
có hai nghiệm phân biệt. Hỏi
S
có bao nhiêu phần tử?
A.
13
. B.
6
. C.
4
. D.
3
.
Câu 24: Cho hình chóp
.
S ABC
có đáy là tam giác vuông đỉnh
B
,
AB a
,
SA
vuông góc với
mặt phẳng đáy và
2
SA a
. Tính khoảng cách từ
A
đến mặt phẳng
SBC
.
A.
5
3
a
. B.
2 5
5
a
. C.
2 2
3
a
. D.
5
5
a
.
Câu 25: Cho mặt cầu bán kính
R
ngoại tiếp một hình lập phương cạnh
.
a
Mệnh đề nào dưới đây
là đúng?
A.
3
R
a
. B.
2
a R
. C.
2
3
R
a
. D.
2 2
a R
.
Câu 26: Một người vay ngân hàng
200
triệu đồng với lãi suất là
0,6%
một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng
9
triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới
9
triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
Trang 4/4 - Mã đề thi 104
A.
22
. B.
25
. C.
23
. D.
24
.
Câu 27: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức
3
2
0
1 ,
t
Q t Q e
với
t
là khoảng thời gian tính bằng giờ và
0
Q
là dung lượng nạp tối đa (pin
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là
0%
) thì sau
bao lâu sẽ nạp được
90%
(kết quả làm tròn đến hàng phần trăm)?
A.
1
t h
B.
1,2
t h
C.
1, 34
t h
D.
1, 54
t h
Câu 28: Cho khối lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác cân với
,
AB AC a
120
BAC
. Mặt phẳng
( )
AB C
tạo với đáy một góc
60
. Tính thể tích
V
của khối lăng trụ đã cho.
A.
3
3
8
a
V
. B.
3
9
8
a
V
. C.
3
3
4
a
V
. D.
3
8
a
V
.
Câu 29: Cho hàm số
4 2
f x ax bx c
với
0
a
,
2019
c
và
2019
a b c
. Tìm
số điểm cực trị của đồ thị hàm số
2019
y f x
.
A.
7
. B.
3
. C.
5
. D.
1
.
Câu 30: Cho lăng trụ
. ' ' '
ABC A B C
có đáy
ABC
là tam giác đều cạnh có độ dài bằng
2.
Hình
chiếu vuông góc của
'
A
lên mặt phẳng
ABC
trùng với trung điểm
H
của
.
BC
Góc tạo bởi
cạnh bên
'
AA
với mặt đáy là
0
45 .
Tính thể tích khối trụ đã cho.
A.
6
.
24
V
B.
3.
V
C.
6
.
8
V
D.
1.
V
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
Câu 32: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
Câu 33: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân
biệt.
Câu 34: Giải bất phương trình
1 1
5 5
log 3 5 log 1
x x
.
Câu 35: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh
bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
Câu 37: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích
xung quanh của hình nón đó.
----------- HẾT ----------
Trang 1/2
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN
ĐÁP ÁN ĐỀ CHÍNH THỨC
(Đáp án có 03 trang)
ĐỀ KIỂM TRA HỌC KỲ I
NĂM HỌC: 2019 - 2020
MÔN: TOÁN - LỚP: 12
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
PHẦN TRẮC NGHIỆM: 6,0 ĐIỂM
CÂU
MÃ
Đ
Ề 101
MÃ
Đ
Ề 102
MÃ
Đ
Ề 103
MÃ
Đ
Ề 104
1 A D B B
2 C A C D
3 A B A C
4 A D D B
5
C
B
C
C
6 B B A D
7 D C D D
8
A
C
B
D
9 B D C A
10 C D D C
11 D B C A
12
D
A
B
A
13 B A D B
14 A D B C
15 B A C C
16 A C D B
17
A
C
B
A
18 C A A A
19 D B A C
20
A
C
D
D
21 C C A B
22 D A D A
23 C D B D
24
D
B
A
B
25 B A C C
26 A C C D
27 B B B D
28 C B A A
29
B
D
A
A
30 D A A B
PHẦN TỰ LUẬN: 4,0 ĐIỂM
Đáp án Điểm
Câu 31: Tìm giá trị cực tiểu
CT
y
của hàm số
4 2
2 3
y x x
.
Ta có:
3 2
0 3
' 4 4 0 4 1 0 1 4
1 4
x y
y x x x x x y
x y
Từ đó suy ra hàm số đạt cực tiểu tại
1
x
và
4
CT
y
.
0,25 x 2
Trang 2/2
Câu 32: Tìm giá trị lớn nhất của hàm số
3 2
2 3 12 2
y x x x
trên đoạn
1;2
.
Ta có
2
1
6 6 12; 0 .
2
x
y x x y
x
0,25
1 15; 1 5; 2 6
y y y
.
1;2
m x
15
a
x
y
.
0,25
Câu 33: Tìm
m
để đường thẳng
y m
cắt đồ thị hàm số
4 2
2 2
y x x
tại bốn điểm phân biệt.
Xét hàm số
0,25
ng th
ẳng cắt đồ thị hàm số tại 4 điểm phân biệt thì
0,25
Câu 34: Giải bất phương trình
1 1
5 5
log 3 5 log 1
x x
.
BPT
5
3 5 0
5
3
3
3 5 1
3
3
x
x
x
x x
x
0,25 x 2
Câu 35: Phương trình
4
log 3.2 1 1
x
x
có hai nghiệm
1 2
,
x
x
. Tính tổng
1 2
x
x
.
PT
2
1
1
3.2 1 4 2 3
4
. 1 0 2 6
4
2
2
x x x x x
.
0,25
Vậy
2
4log
2
6x
. Ta có
1 2
2
x
x
0,25
Câu 36: Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình chữ nhật,
, 2 ,
AB a BC a
cạnh bên
SA
vuông góc với đáy và
2
SA
a
. Tính thể tích khối chóp
. .
S ABCD
3
1 1 2 2
. .2 . 2
3 3 3
a
V Sh a a a
0,25 x 2
Câu 37: Cho hình trụ có diện tích xung quanh bằng
50
và có độ dài đường sinh bằng đường kính
của đường tròn đáy. Tính bán kính
r
của đường tròn đáy.
2
5 2
2 2 .2 4 50
2
xq
S rl r r r r
0,25 x 2
Câu 38: Cho hình nón có bán kính đáy bằng
a
và độ dài đường sinh bằng
2
a
. Tính diện tích xung
quanh của hình nón đó.
2
. .2 2
xq
S Rl a a a
0,25 x 2
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm tương ứng theo từng phần.
4 2
2 2
y x x
3
0 2
4 4 , cho 0
1 1
x y
y x x y
x y
+
_
-∞
0
0
1
0
1
- 1
1
+ ∞
+ ∞
_
0
2
+
+∞
y
y'
x
y m
1 2.
m
| 1/18
| | Tải xuống

Có thể bạn quan tâm:

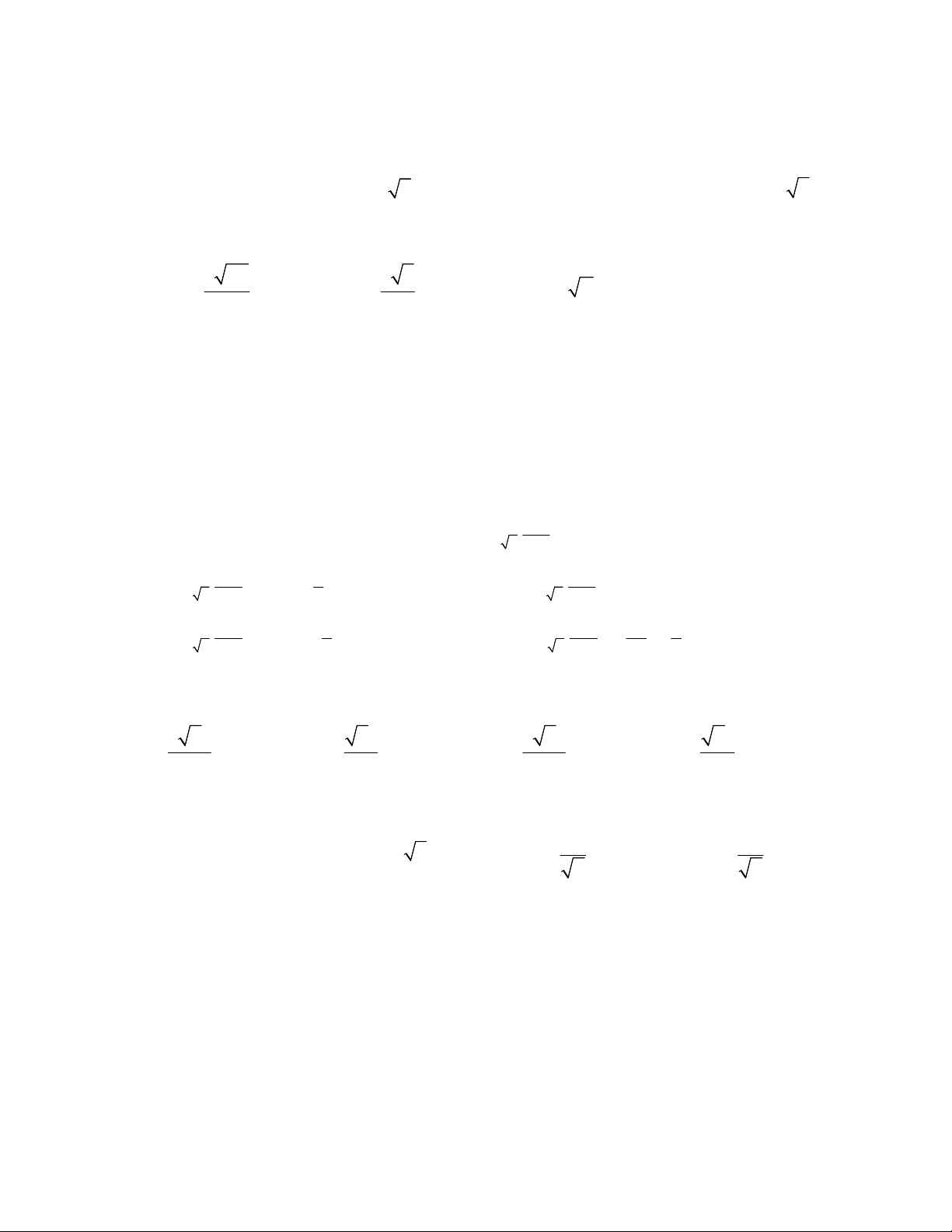
Preview text:

TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2019 – 2020 ĐỀ CHÍ NH THỨC MÔN: TOÁN – LỚP: 12 (Đề thi có 04 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Mã đề thi 101
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   . A. maxy  15. B. maxy  6 C. maxy  11. D. maxy  10.  1  ;2    1  ;2    1  ;2    1  ;2   x x
Câu 2: Tính tổng các nghiệm của phương trình 2  3  2  3  14. A. 2 B. 4 C. 0 D. 2
Câu 3: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,AB  a, BC  2 , a cạnh bên
SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD. 3 2a 2 3 2a 3 A. . B. . C. 3 2a 2 . D. 3 a 2 . 3 3
Câu 4: Tìm tập xác định của hàm số y   2 ln x  3x  2. A.  ;  1 2;. B. 1;2. C.  ;  1  2;   .. D. 1;2   .
Câu 5: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3. A. C y T  3. B. C y T  4 . C. C y T  4. D. C y T  3.
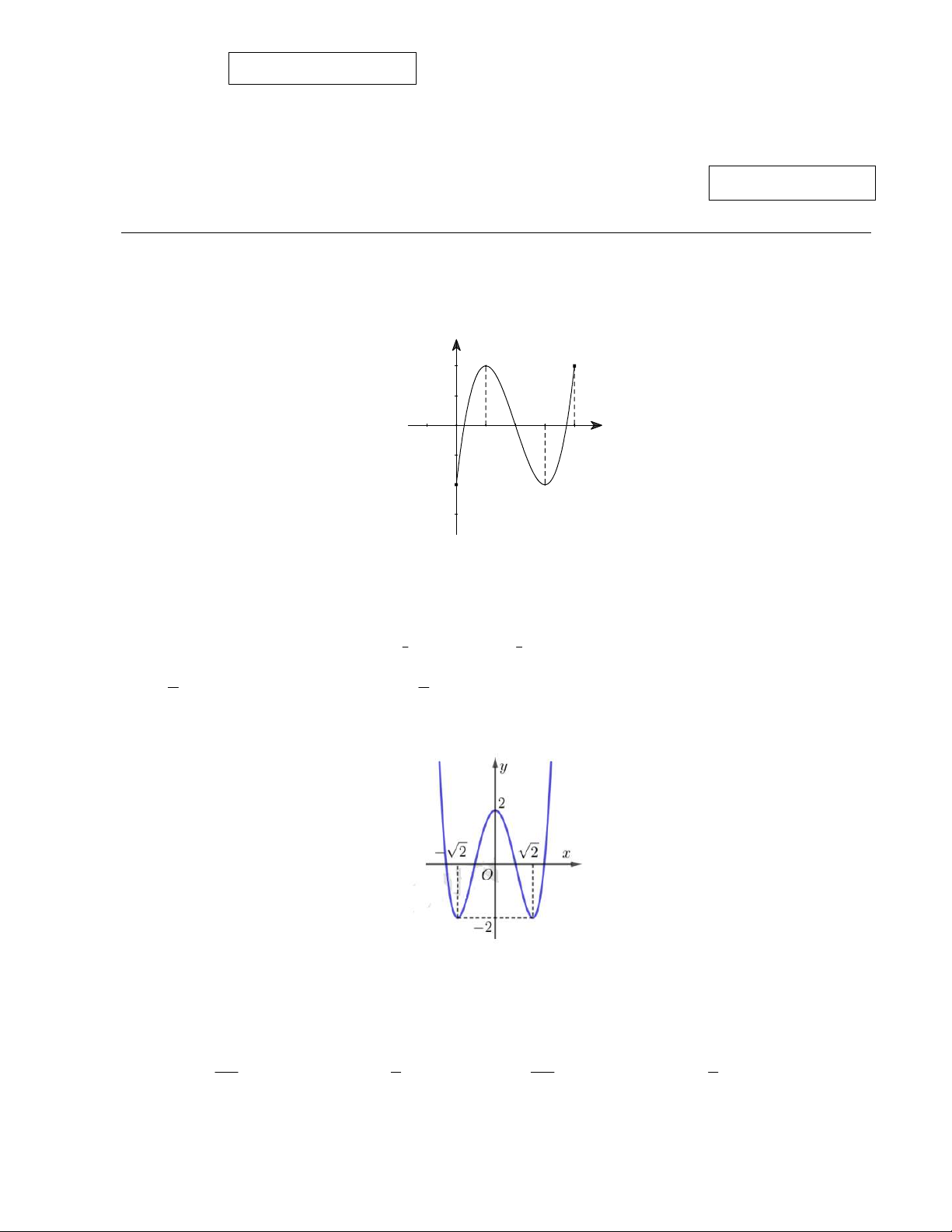
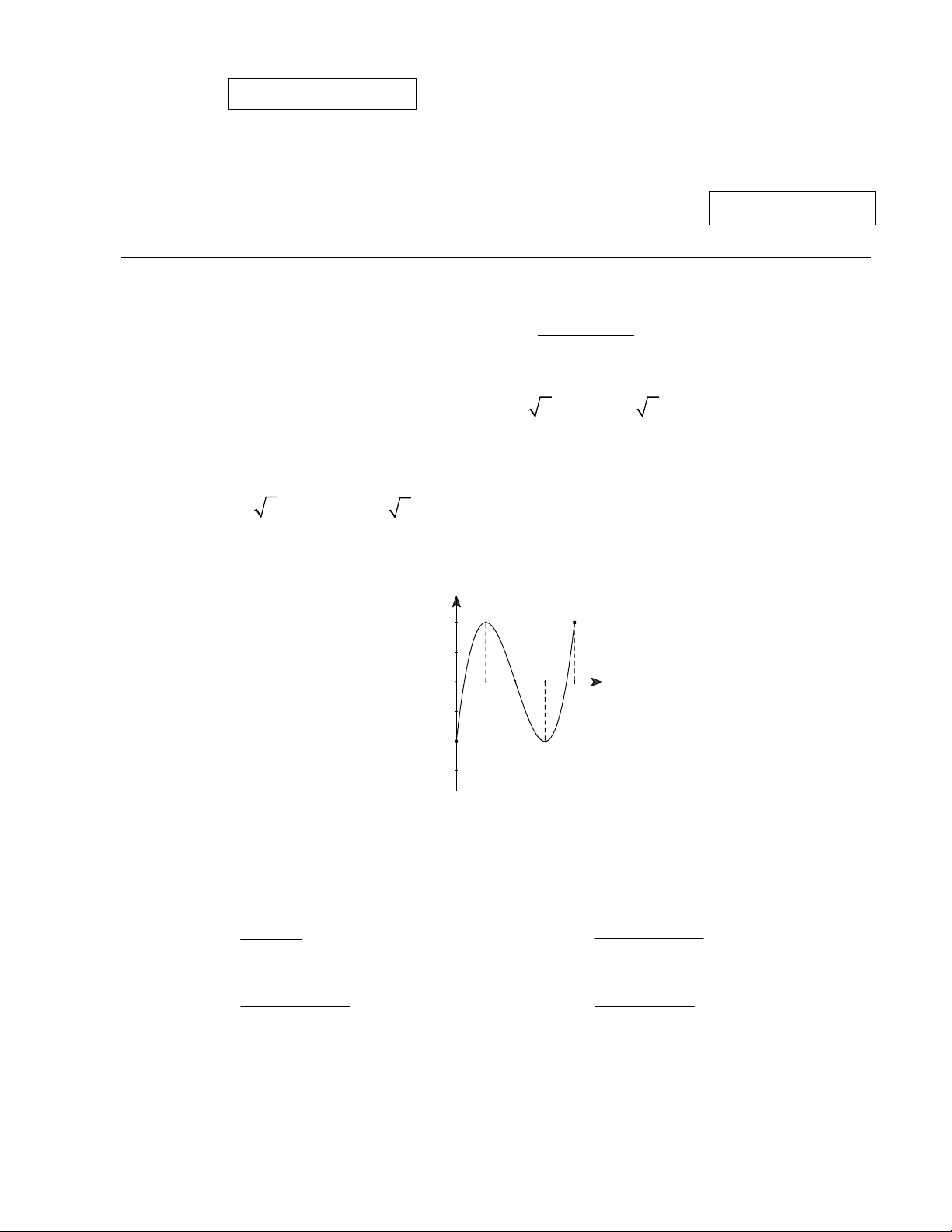
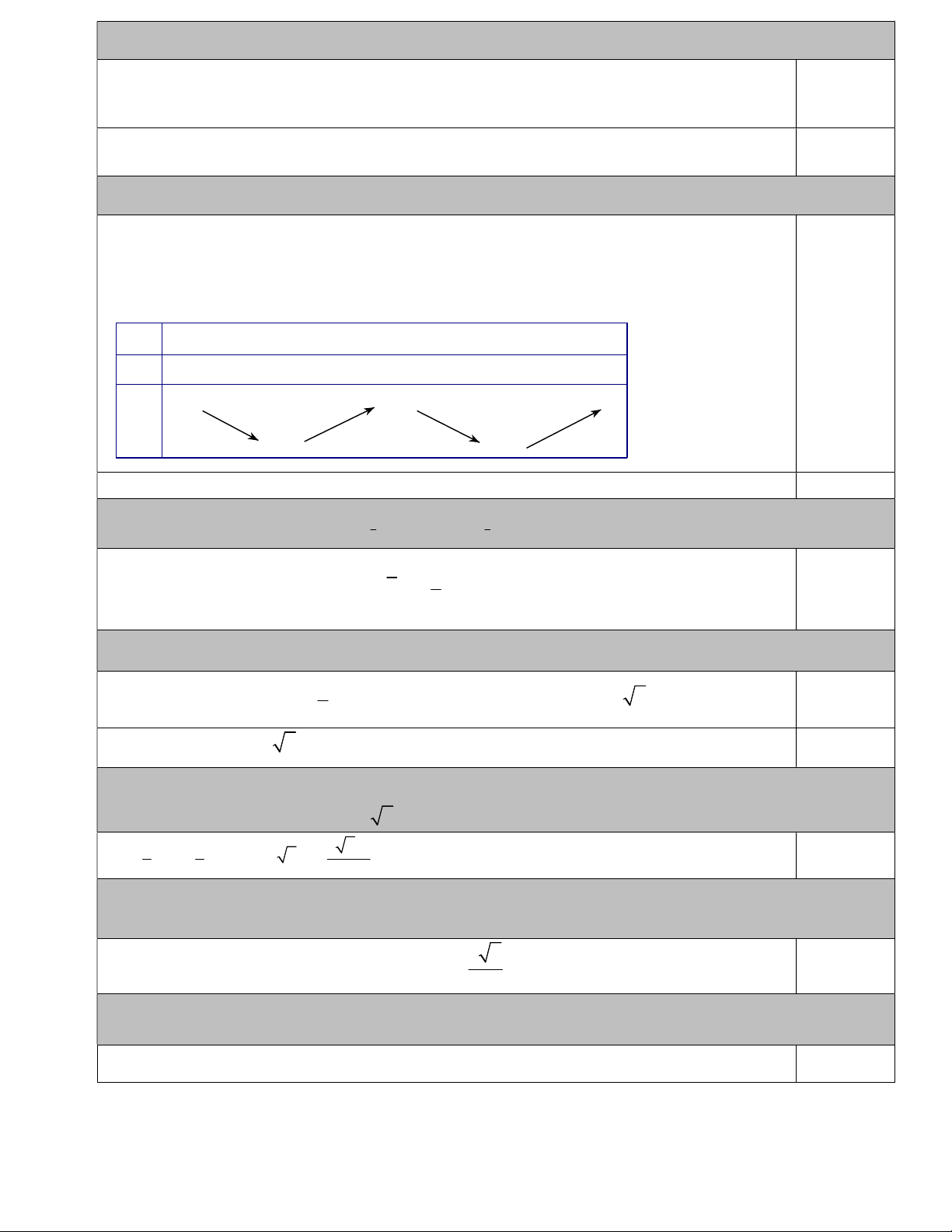
Câu 6: Cho hàm số y  f x  liên tục trên đoạn 0;4 
 có đồ thị như hình vẽ. y O 2 3 x 1 4 -2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  0 .
B. Hàm số đạt cực tiểu tại x  3 .
C. Hàm số đạt cực đại tại x  4 .
D. Hàm số đạt cực đại tại x  2.
Câu 7: Tính đạo hàm của hàm số f x   log  2 2 x  2x . ln2 1 A. f x   . B. f x   . 2 x  2x  2x 2xln2
Trang 1/4 - Mã đề thi 101 2x  2 ln2 2x  2 C. f x     . D. f x   . 2 x  2x  2x 2xln2 x  1
Câu 8: Viết phương trình tiếp tuyến với đồ thị hàm số y 
biết tiếp tuyến song song với x  1
đường thẳng  : 2x  y  1  0. A. y  2x  7 B. y  2x  7 C. y  2x  1 D. y  2x Câu 9: Cho hàm số
y  f x  liên trục trên  và có đạo hàm
f x   x  x  2 x  2017 ' 1 2 3
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số nghịch biến trên khoảng 1;3.
C. Hàm số đồng biến trên các khoảng 1;2và 3;.
D. Hàm số đạt cực đại tại x  2, đạt cực tiểu tại x  1 và x  3.
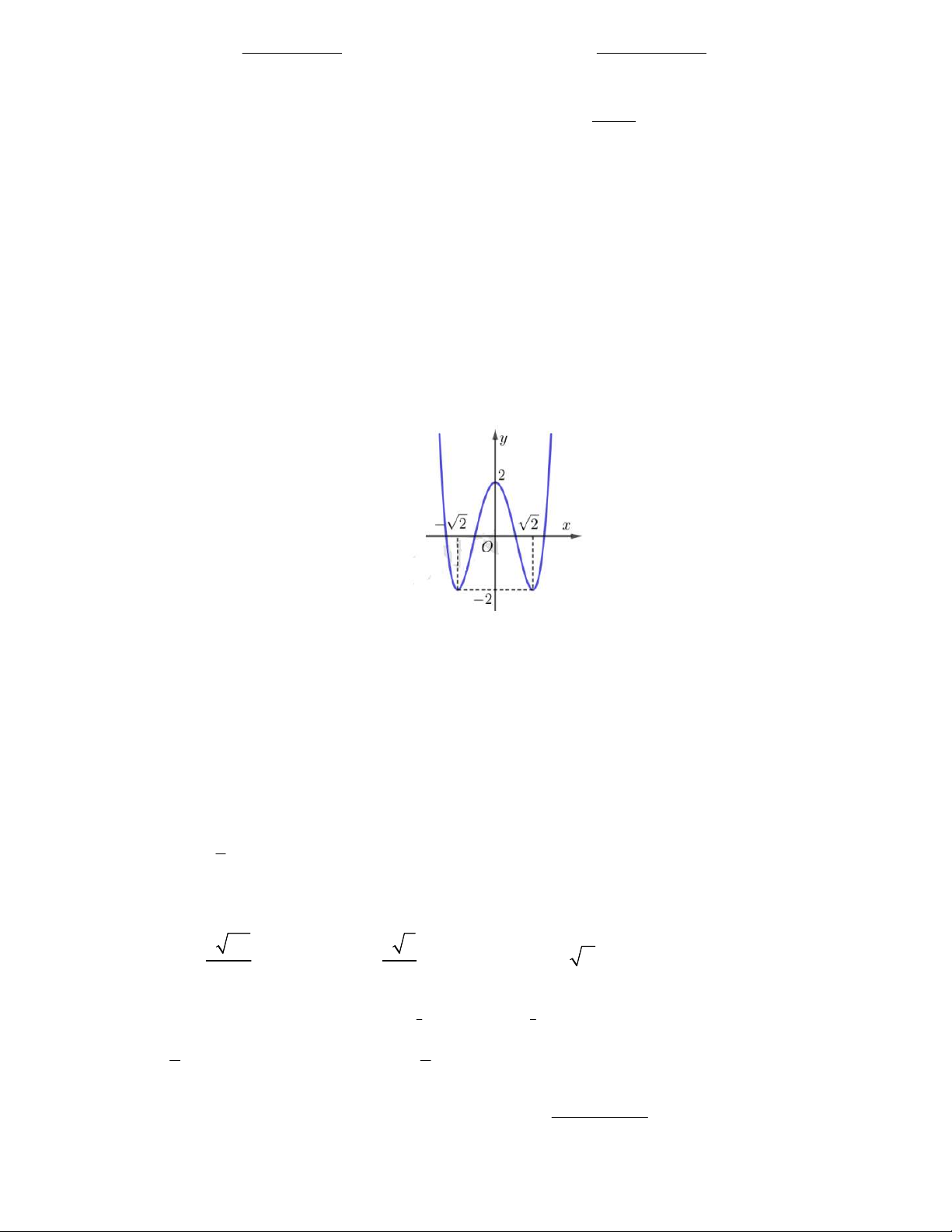
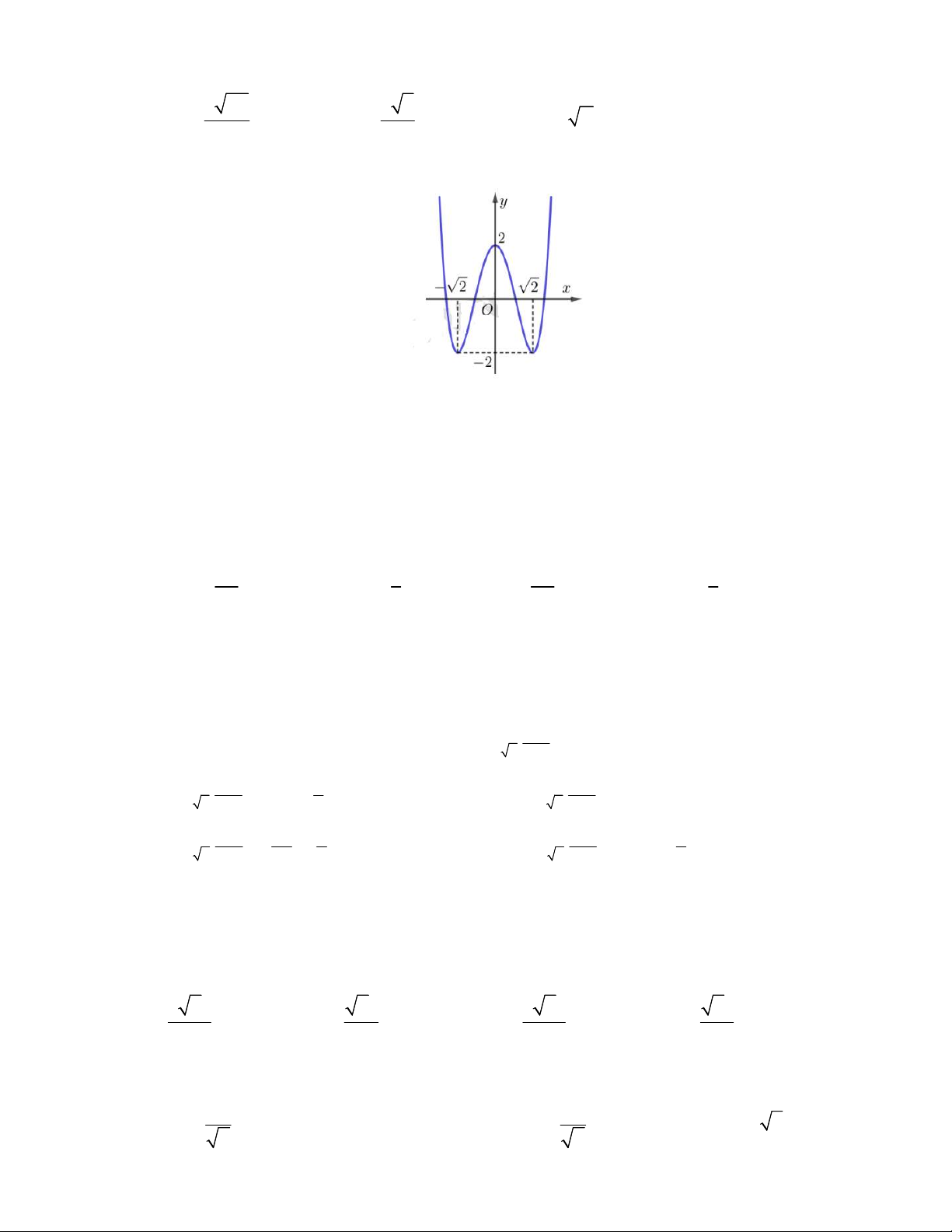
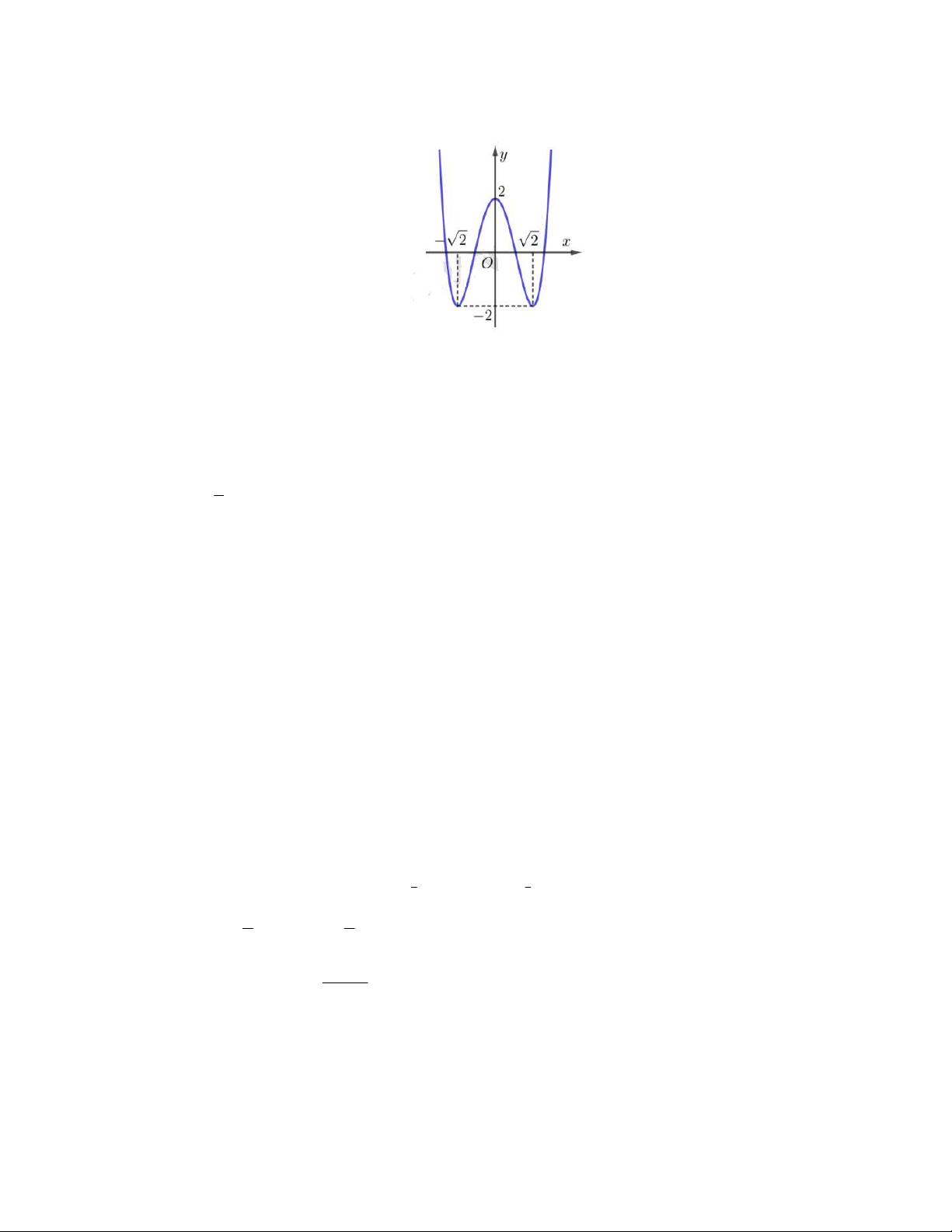
Câu 10: Đường cong trong hình bên là đồ thị của hàm số nào? A. 4 2 y  x  4x  2 B. 4 2 y  x   4x  2 C. 4 2 y  x  4x  2 D. 4 2 y  x  4x  2
Câu 11: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích
xung quanh của hình nón đó. A. 2 3 a  B. 2 2a C. 2 4 a  D. 2 2 a 
Câu 12: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập  ? A. y  log 2 2 x  1. B. y  log2 x  1. 1 x C. y      . x  D. y  log2 2  1. 2
Câu 13: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r   . B. r  . C. r  5 . D. r  5. 2 2
Câu 14: Giải bất phương trình sau log 3x  5  log x  1 . 1   1   5 5 A. 5  x  3 B. 5 1   x  . C. x  3. D. 1  x  3 . 3 3 2 x  3x  2
Câu 15: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 x  4 A. 1 B. 2 C. 0 D. 3
Trang 2/4 - Mã đề thi 101
Câu 16: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt. A. 1  m  2 . B. m  2 . C. m  2 . D. 2  m  3.
Câu 17: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 3 mặt phẳng. B. 4 mặt phẳng. C. 6 mặt phẳng. D. 9 mặt phẳng. x  3 Câu 18: Cho hàm số y 
. Khẳng định nào sau đây là đúng? x  2
A. Hàm số đồng biến trên  \ 2.
B. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
C. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
D. Hàm số đồng biến trên khoảng ( ;  2)  (2;).
Câu 19: Tìm tập nghiệm của bất phương trình 5x 1 2   4.  1    1  1   1  A.  ;           . B.  ;  . C.  ;. D.  ;.  5   5  5  5  Câu 20: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 . A. 2 . B. 6  4 2 . C. 4 . D. lo 2 g 6  4 2.
Câu 21: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 6 . B. 13 . C. 3 . D. 4 .
Câu 22: Cho mặt cầu bán kính R ngoại tiếp một hình lập phương cạnh a. Mệnh đề nào dưới đây là đúng? R 2R A. a  2R 2 . B. a  . C. a  2R . D. a  . 3 3 121
Câu 23: Cho log49 11  a ; lo 2 g 7  b . Tính log3 theo a, b . 7 8 121 9 121 A. log3  3a  . B. log  12a  9b 7 8 b 3 7 8 121 9 121 1 3 C. log3  12a  D. log   . 7 8 b 3 7 8 3a b
Câu 24: Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với
mặt phẳng đáy và SA  2a . Tính khoảng cách từ A đến mặt phẳng SBC . 5a 5a 2 2a 2 5a A. . B. . C. . D. . 3 5 3 5
Câu 25: Tìm số nghiệm của phương trình 2 lo 2 g x  2log2 3x  4. A. 0 . B. 1 . C. 2 . D. 3 .
Câu 26: Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân với AB  AC  a, 
BAC  120. Mặt phẳng (AB C
 ) tạo với đáy một góc 60. Tính thể tích V
của khối lăng trụ đã cho. 3 3a 3 9a 3 a 3 3a A. V  . B. V  . C. V  . D. V  . 8 8 8 4
Trang 3/4 - Mã đề thi 101 Câu 27: Cho hàm số   4 2
f x  ax  bx  c với a  0 , c  2019 và a b  c  2019 . Tìm
số điểm cực trị của đồ thị hàm số y  f x   2019 . A. 1 . B. 7 . C. 3 . D. 5 .
Câu 28: Một người vay ngân hàng 200 triệu đồng với lãi suất là 0,6% một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng. A. 22 . B. 23 . C. 24 . D. 25 .
Câu 29: Cho lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh có độ dài bằng 2. Hình
chiếu vuông góc của A' lên mặt phẳng ABC  trùng với trung điểm H của BC. Góc tạo bởi
cạnh bên AA' với mặt đáy là 0
45 . Tính thể tích khối trụ đã cho. 6 6 A. V  1. B. V  3. C. V  . D. V  . 24 8
Câu 30: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức  3t  Q t      2 Q    với 0 1 e ,  
t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin     0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0% ) thì sau
bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t  1h B. t  1,2h C. t  1,34h D. t  1,54h
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3.
Câu 32: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   .
Câu 33: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt.
Câu 34: Giải bất phương trình log 3x  5  log x  1 . 1   1   5 5 Câu 35: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 .
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2a, cạnh
bên SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD.
Câu 37: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích
xung quanh của hình nón đó. ----------- HẾT ----------
Trang 4/4 - Mã đề thi 101
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2019 – 2020 ĐỀ CHÍ NH THỨC MÔN: TOÁN – LỚP: 12 (Đề thi có 04 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Mã đề thi 102
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Cho hàm số y  f x  liên tục trên đoạn 0;4 
 có đồ thị như hình vẽ. y O 2 3 x 1 4 -2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực tiểu tại x  0 .
B. Hàm số đạt cực đại tại x  2 .
C. Hàm số đạt cực đại tại x  4 .
D. Hàm số đạt cực tiểu tại x  3 .
Câu 2: Giải bất phương trình sau log 3x  5  log x  1 . 1   1   5 5 5 5 A.  x  3 B. 1   x  . C. x  3. D. 1  x  3 . 3 3
Câu 3: Đường cong trong hình bên là đồ thị của hàm số nào? A. 4 2 y  x   4x  2 B. 4 2 y  x  4x  2 C. 4 2 y  x  4x  2 D. 4 2 y  x  4x  2
Câu 4: Tìm tập nghiệm của bất phương trình 5x 1 2   4.  1    1  1   1  A.  ;           . B.  ;  . C.  ;. D.  ;.  5   5  5  5 
Câu 5: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập  ? A. y  log  2 x 2 x  1. B. y  log2 2  1.
Trang 1/4 - Mã đề thi 102  1 x C. y      .  D. y  log2 x  1. 2  2 x  3x  2
Câu 6: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 x  4 A. 1 B. 2 C. 0 D. 3 x  1
Câu 7: Viết phương trình tiếp tuyến với đồ thị hàm số y 
biết tiếp tuyến song song với x  1
đường thẳng  : 2x  y  1  0. A. y  2x  1 B. y  2x C. y  2x  7 D. y  2x  7
Câu 8: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật,AB  a, BC  2a, cạnh bên
SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD. 3 2a 3 3 2a 2 A. 3 2a 2 . B. . C. . D. 3 a 2 . 3 3 x x
Câu 9: Tính tổng các nghiệm của phương trình 2  3  2  3  14. A. 2 B. 2 C. 4 D. 0
Câu 10: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích xung quanh của hình nón đó. A. 2 3 a  B. 2 2a C. 2 4 a  D. 2 2 a 
Câu 11: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   . A. maxy  11. B. maxy  15. C. maxy  10. D. maxy  6  1  ;2    1  ;2    1  ;2    1  ;2  
Câu 12: Tính đạo hàm của hàm số f x   log  2 2 x  2x . 2x  2 2x  2 ln2 A. f x    . B. f x     . 2 x  2x ln2 2 x  2x ln2 1 C. f x   . D. f x   . 2 x  2x  2x 2xln2
Câu 13: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 3 mặt phẳng. B. 4 mặt phẳng. C. 6 mặt phẳng. D. 9 mặt phẳng.
Câu 14: Tìm tập xác định của hàm số y   2 ln x  3x  2. A.  ;  1  2;   .. B. 1;2   . C. 1;2. D.  ;  1 2;.
Câu 15: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt. A. 1  m  2 . B. m  2 . C. m  2 . D. 2  m  3.
Câu 16: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3. A. C y T  3. B. C y T  3. C. C y T  4. D. C y T  4 . x  3 Câu 17: Cho hàm số y 
. Khẳng định nào sau đây là đúng? x  2
Trang 2/4 - Mã đề thi 102
A. Hàm số đồng biến trên  \ 2.
B. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
C. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
D. Hàm số đồng biến trên khoảng ( ;  2)  (2;). Câu 18: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 . A. 2 . B. 6  4 2 . C. 4 . D. lo 2 g 6  4 2.
Câu 19: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r   . B. r  . C. r  5 . D. r  5. 2 2 Câu 20: Cho hàm số
y  f x  liên trục trên  và có đạo hàm
f x   x  x  2 x  2017 ' 1 2 3
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng 1;2và 3;.
C. Hàm số nghịch biến trên khoảng 1;3.
D. Hàm số đạt cực đại tại x  2, đạt cực tiểu tại x  1 và x  3. 121
Câu 21: Cho log49 11  a ; lo 2 g 7  b . Tính log3 theo a, b . 7 8 121 9 121 A. log3  3a  . B. log  12a  9b 7 8 b 3 7 8 121 9 121 1 3 C. log3  12a  D. log   . 7 8 b 3 7 8 3a b
Câu 22: Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với
mặt phẳng đáy và SA  2a . Tính khoảng cách từ A đến mặt phẳng SBC . 2 5a 5a 2 2a 5a A. . B. . C. . D. . 5 5 3 3
Câu 23: Cho mặt cầu bán kính R ngoại tiếp một hình lập phương cạnh a. Mệnh đề nào dưới đây là đúng? R 2R A. a  2R . B. a  2R 2 . C. a  . D. a  . 3 3
Câu 24: Tìm số nghiệm của phương trình 2
log2 x  2log2 3x  4. A. 0 . B. 1 . C. 2 . D. 3 .
Câu 25: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 3 . B. 6 . C. 13 . D. 4 .
Câu 26: Một người vay ngân hàng 200 triệu đồng với lãi suất là 0,6% một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng. A. 22 . B. 23 . C. 24 . D. 25 .
Trang 3/4 - Mã đề thi 102
Câu 27: Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân với AB  AC  a, 
BAC  120. Mặt phẳng (AB C
 ) tạo với đáy một góc 60. Tính thể tích V
của khối lăng trụ đã cho. 3 3a 3 3a 3 9a 3 a A. V  . B. V  . C. V  . D. V  . 4 8 8 8
Câu 28: Cho lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh có độ dài bằng 2. Hình
chiếu vuông góc của A' lên mặt phẳng ABC  trùng với trung điểm H của BC. Góc tạo bởi
cạnh bên AA' với mặt đáy là 0
45 . Tính thể tích khối trụ đã cho. 6 6 A. V  1. B. V  3. C. V  . D. V  . 24 8
Câu 29: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức  3t  Q t      2 Q    với 0 1 e ,  
t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin     0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0% ) thì sau
bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t  1h B. t  1,2h C. t  1,34h D. t  1,54h Câu 30: Cho hàm số   4 2
f x  ax  bx  c với a  0 , c  2019 và a  b  c  2019 . Tìm
số điểm cực trị của đồ thị hàm số y  f x   2019 . A. 7 . B. 5 . C. 1 . D. 3 .
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3.
Câu 32: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   .
Câu 33: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt.
Câu 34: Giải bất phương trình log 3x  5  log x  1 . 1   1   5 5 Câu 35: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 .
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2a, cạnh
bên SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD.
Câu 37: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích
xung quanh của hình nón đó. ----------- HẾT ----------
Trang 4/4 - Mã đề thi 102
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2019 – 2020 ĐỀ CHÍ NH THỨC MÔN: TOÁN – LỚP: 12 (Đề thi có 04 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Mã đề thi 103
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm)
Câu 1: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích xung quanh của hình nón đó. A. 2 2a B. 2 2 a  C. 2 4 a  D. 2 3 a 
Câu 2: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2 , a cạnh bên
SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD. 3 2a 3 3 2a 2 A. 3 2a 2 . B. . C. . D. 3 a 2 . 3 3 Câu 3: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 . A. 2 . B. 4 . C. lo 2
g 6  4 2. D. 6  4 2 . x x
Câu 4: Tính tổng các nghiệm của phương trình 2  3  2  3  14. A. 2 B. 2 C. 4 D. 0 x  1
Câu 5: Viết phương trình tiếp tuyến với đồ thị hàm số y 
biết tiếp tuyến song song với x  1
đường thẳng  : 2x  y  1  0. A. y  2x  1 B. y  2x C. y  2x  7 D. y  2x  7
Câu 6: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập  ? 1 x A. log x y     2 2  1. B. y   .  2 C. y  log  2 2 x  1. D. y  log2 x  1.
Câu 7: Tính đạo hàm của hàm số f x   log  2 2 x  2x . 1 2x  2 ln2 A. f x    . B. f x     . 2 x  2x ln2 2 x  2x ln2 2x  2 C. f x   . D. f x   . 2 x  2x  2x 2xln2
Câu 8: Cho hàm số y  f x  liên tục trên đoạn 0;4 
 có đồ thị như hình vẽ.
Trang 1/4 - Mã đề thi 104 y O 2 3 x 1 4 -2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại x  2 .
B. Hàm số đạt cực tiểu tại x  3 .
C. Hàm số đạt cực tiểu tại x  0 .
D. Hàm số đạt cực đại tại x  4 .
Câu 9: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3. A. C y T  3. B. C y T  3. C. C y T  4. D. C y T  4 .
Câu 10: Tìm tập xác định của hàm số y   2 ln x  3x  2. A.  ;  1  2;   .. B. 1;2   . C. 1;2. D.  ;  1 2;. Câu 11: Cho hàm số
y  f x  liên trục trên  và có đạo hàm
f x   x  x  2 x  2017 ' 1 2 3
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng 1;2 và 3;.
C. Hàm số nghịch biến trên khoảng 1;3.
D. Hàm số đạt cực đại tại x  2, đạt cực tiểu tại x  1 và x  3.
Câu 12: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng? A. 6 mặt phẳng. B. 3 mặt phẳng. C. 4 mặt phẳng. D. 9 mặt phẳng.
Câu 13: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   . A. maxy  11. B. maxy  10. C. maxy  6 D. maxy  15.  1  ;2    1  ;2    1  ;2    1  ;2  
Câu 14: Giải bất phương trình sau log 3x  5  log x  1 . 1   1   5 5 5 5 A. 1   x  . B.  x  3 C. x  3. D. 1  x  3 . 3 3 x  3 Câu 15: Cho hàm số y 
. Khẳng định nào sau đây là đúng? x  2
A. Hàm số đồng biến trên  \ 2.
B. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
C. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
D. Hàm số đồng biến trên khoảng ( ;  2)  (2;). 2 x  3x  2
Câu 16: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 x  4
Trang 2/4 - Mã đề thi 104 A. 3 B. 1 C. 0 D. 2
Câu 17: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r   . B. r  . C. r  5 . D. r  5. 2 2
Câu 18: Đường cong trong hình bên là đồ thị của hàm số nào? A. 4 2 y  x  4x  2 B. 4 2 y  x  4x  2 C. 4 2 y  x   4x  2 D. 4 2 y  x  4x  2
Câu 19: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt. A. 1  m  2 . B. m  2 . C. m  2 . D. 2  m  3.
Câu 20: Tìm tập nghiệm của bất phương trình 5x 1 2   4.  1    1  1   1  A.  ;           . B.  ;  . C.  ;. D.  ;.  5   5  5  5 
Câu 21: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 3 . B. 6 . C. 13 . D. 4 . 121
Câu 22: Cho log49 11  a ; lo 2 g 7  b . Tính log3 theo a, b . 7 8 121 9 121 A. log3  3a  . B. log  12a  9b 7 8 b 3 7 8 121 1 3 121 9 C. log3   . D. log  12a  7 8 3a b 3 7 8 b
Câu 23: Tìm số nghiệm của phương trình 2
log2 x  2log2 3x  4. A. 0 . B. 1 . C. 2 . D. 3 .
Câu 24: Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với
mặt phẳng đáy và SA  2a . Tính khoảng cách từ A đến mặt phẳng SBC . 2 5a 5a 2 2a 5a A. . B. . C. . D. . 5 3 3 5
Câu 25: Cho mặt cầu bán kính R ngoại tiếp một hình lập phương cạnh a. Mệnh đề nào dưới đây là đúng? R 2R A. a  . B. a  2R . C. a  . D. a  2R 2 . 3 3
Trang 3/4 - Mã đề thi 104
Câu 26: Một người vay ngân hàng 200 triệu đồng với lãi suất là 0,6% một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng. A. 23 . B. 25. C. 24. D. 22.
Câu 27: Cho lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh có độ dài bằng 2. Hình
chiếu vuông góc của A' lên mặt phẳng ABC  trùng với trung điểm H của BC. Góc tạo bởi
cạnh bên AA' với mặt đáy là 0
45 . Tính thể tích khối trụ đã cho. 6 6 A. V  1. B. V  3. C. V  . D. V  . 24 8 Câu 28: Cho hàm số   4 2
f x  ax  bx  c với a  0, c  2019 và a b  c  2019 . Tìm
số điểm cực trị của đồ thị hàm số y  f x   2019 . A. 7 . B. 5 . C. 1 . D. 3 .
Câu 29: Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân với AB  AC  a, 
BAC  120. Mặt phẳng (AB C
 ) tạo với đáy một góc 60. Tính thể tích V
của khối lăng trụ đã cho. 3 3a 3 9a 3 3a 3 a A. V  . B. V  . C. V  . D. V  . 8 8 4 8
Câu 30: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức  3t  Q t      2 Q    với 0 1 e ,  
t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin     0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0% ) thì sau
bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t  1,54h B. t  1,2h C. t  1h D. t  1,34h
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3.
Câu 32: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   .
Câu 33: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt.
Câu 34: Giải bất phương trình log 3x  5  log x  1 . 1   1   5 5 Câu 35: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 .
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2a, cạnh
bên SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD.
Câu 37: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích
xung quanh của hình nón đó. ----------- HẾT ----------
Trang 4/4 - Mã đề thi 104
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC: 2019 – 2020 ĐỀ CHÍ NH THỨC MÔN: TOÁN – LỚP: 12 (Đề thi có 04 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề) Mã đề thi 104
Họ và tên thí sinh: …………………………………………. Số báo danh: ………………………….
PHẦN TRẮC NGHIỆM (6,0 điểm) 2 x  3x  2
Câu 1: Tìm số đường tiệm cận của đồ thị hàm số y  . 2 x  4 A. 1 B. 2 C. 0 D. 3 x x
Câu 2: Tính tổng các nghiệm của phương trình 2  3  2  3  14. A. 2 B. 2 C. 4 D. 0 Câu 3: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 . A. lo 2
g 6  4 2. B. 6  4 2 . C. 2 . D. 4 .
Câu 4: Cho hàm số y  f x  liên tục trên đoạn 0;4 
 có đồ thị như hình vẽ. y O 2 3 x 1 4 -2
Mệnh đề nào sau đây đúng?
A. Hàm số đạt cực đại tại x  2 .
B. Hàm số đạt cực tiểu tại x  3 .
C. Hàm số đạt cực tiểu tại x  0 .
D. Hàm số đạt cực đại tại x  4 .
Câu 5: Tính đạo hàm của hàm số f x   log  2 2 x  2x . ln2 1 A. f x   . B. f x   . 2 x  2x  2x 2xln2 2x  2 2x  2 ln2 C. f x    . D. f x     . 2 x  2x ln2 2 x  2x
Câu 6: Tìm tập xác định của hàm số y   2 ln x  3x  2. A.  ;  1  2;   .. B. 1;2   . C. 1;2. D.  ;  1 2;.
Trang 1/4 - Mã đề thi 104
Câu 7: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   . A. maxy  11. B. maxy  10. C. maxy  6 D. maxy  15.  1  ;2    1  ;2    1  ;2    1  ;2  
Câu 8: Đường cong trong hình bên là đồ thị của hàm số nào? A. 4 2 y  x  4x  2 B. 4 2 y  x   4x  2 C. 4 2 y  x  4x  2 D. 4 2 y  x  4x  2
Câu 9: Trong các hàm số dưới đây, hàm số nào đồng biến trên tập  ? A. log x y  2 2  1. B. y  log2 x  1.  1 x C. y      . 2  D. y  log2 x  1. 2  Câu 10: Cho hàm số
y  f x  liên trục trên  và có đạo hàm
f x   x  x  2 x  2017 ' 1 2 3
. Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số có ba điểm cực trị.
B. Hàm số đồng biến trên các khoảng 1;2 và 3;.
C. Hàm số nghịch biến trên khoảng 1;3.
D. Hàm số đạt cực đại tại x  2, đạt cực tiểu tại x  1 và x  3.
Câu 11: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích xung quanh của hình nón đó. A. 2 2 a  B. 2 2a C. 2 4 a  D. 2 3 a 
Câu 12: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3. A. C y T  4. B. C y T  3. C. C y T  4 . D. C y T  3.
Câu 13: Giải bất phương trình sau log 3x  5  log x  1 . 1   1   5 5 5 5 A. 1   x  . B.  x  3 C. x  3. D. 1  x  3 . 3 3 x  3 Câu 14: Cho hàm số y 
. Khẳng định nào sau đây là đúng? x  2
A. Hàm số đồng biến trên  \ 2.
B. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
C. Hàm số nghịch biến trên mỗi khoảng ( ;  2) và (2; )  .
D. Hàm số đồng biến trên khoảng ( ;  2)  (2;).
Câu 15: Hình hộp chữ nhật có ba kích thước đôi một khác nhau có bao nhiêu mặt phẳng đối xứng?
Trang 2/4 - Mã đề thi 104 A. 6 mặt phẳng. B. 4 mặt phẳng. C. 3 mặt phẳng. D. 9 mặt phẳng.
Câu 16: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy. 5 2 5 2 A. r   . B. r  . C. r  5 . D. r  5. 2 2
Câu 17: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2 , a cạnh
bên SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD. 3 2a 2 3 2a 3 A. . B. 3 a 2 . C. . D. 3 2a 2 . 3 3
Câu 18: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt. A. 1  m  2 . B. m  2 . C. m  2 . D. 2  m  3. x  1
Câu 19: Viết phương trình tiếp tuyến với đồ thị hàm số y 
biết tiếp tuyến song song với x  1
đường thẳng  : 2x  y  1  0. A. y  2x  7 B. y  2x C. y  2x  7 D. y  2x  1
Câu 20: Tìm tập nghiệm của bất phương trình 5x 1 2   4.  1    1  1   1  A.  ;           . B.  ;  . C.  ;. D.  ;.  5   5  5  5 
Câu 21: Tìm số nghiệm của phương trình 2
log2 x  2log2 3x  4. A. 2 . B. 1 . C. 3 . D. 0 . 121
Câu 22: Cho log49 11  a ; lo 2 g 7  b . Tính log3 theo a, b . 7 8 121 9 121 1 3 A. log3  12a  B. log   . 7 8 b 3 7 8 3a b 121 121 9 C. log3  12a  9b D. log  3a  . 7 8 3 7 8 b
Câu 23: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình x x 1  2 16  m.4
 5m  45  0 có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử? A. 13 . B. 6 . C. 4 . D. 3 .
Câu 24: Cho hình chóp S.ABC có đáy là tam giác vuông đỉnh B , AB  a , SA vuông góc với
mặt phẳng đáy và SA  2a . Tính khoảng cách từ A đến mặt phẳng SBC . 5a 2 5a 2 2a 5a A. . B. . C. . D. . 3 5 3 5
Câu 25: Cho mặt cầu bán kính R ngoại tiếp một hình lập phương cạnh a. Mệnh đề nào dưới đây là đúng? R 2R A. a  . B. a  2R . C. a  . D. a  2R 2 . 3 3
Câu 26: Một người vay ngân hàng 200 triệu đồng với lãi suất là 0,6% một tháng theo thỏa
thuận: Sau đúng một tháng kể từ ngày vay thì ông bắt đầu trả nợ và đều đặn cứ mỗi tháng người
đó sẽ trả cho ngân hàng 9 triệu đồng cho đến khi hết nợ (biết rằng, tháng cuối cùng có thể trả
dưới 9 triệu đồng). Hỏi sau bao nhiêu tháng thì người đó trả được hết nợ ngân hàng.
Trang 3/4 - Mã đề thi 104 A. 22 . B. 25 . C. 23 . D. 24 .
Câu 27: Một điện thoại đang nạp pin, dung lượng nạp được tính theo công thức  3t  Q t      2 Q    với 0 1 e ,  
t là khoảng thời gian tính bằng giờ và Q là dung lượng nạp tối đa (pin     0
đầy). Nếu điện thoại nạp pin từ lúc cạn pin (tức là dung lượng pin lúc bắt đầu nạp là 0% ) thì sau
bao lâu sẽ nạp được 90% (kết quả làm tròn đến hàng phần trăm)? A. t  1h B. t  1,2h C. t  1,34h D. t  1,54h
Câu 28: Cho khối lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác cân với AB  AC  , a 
BAC  120. Mặt phẳng (AB C
 ) tạo với đáy một góc 60. Tính thể tích V
của khối lăng trụ đã cho. 3 3a 3 9a 3 3a 3 a A. V  . B. V  . C. V  . D. V  . 8 8 4 8 Câu 29: Cho hàm số   4 2
f x  ax  bx  c với a  0 , c  2019 và a  b  c  2019 . Tìm
số điểm cực trị của đồ thị hàm số y  f x   2019 . A. 7 . B. 3 . C. 5 . D. 1 .
Câu 30: Cho lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh có độ dài bằng 2. Hình
chiếu vuông góc của A' lên mặt phẳng ABC  trùng với trung điểm H của BC. Góc tạo bởi
cạnh bên AA' với mặt đáy là 0
45 . Tính thể tích khối trụ đã cho. 6 6 A. V  . B. V  3. C. V  . D. V  1. 24 8
PHẦN TỰ LUẬN (4,0 điểm)
Câu 31: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3.
Câu 32: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   .
Câu 33: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt.
Câu 34: Giải bất phương trình log 3x  5  log x  1 . 1   1   5 5 Câu 35: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 .
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2a, cạnh
bên SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD.
Câu 37: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường
kính của đường tròn đáy. Tính bán kính r của đường tròn đáy.
Câu 38: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích
xung quanh của hình nón đó. ----------- HẾT ----------
Trang 4/4 - Mã đề thi 104
TRƯỜNG TRUNG HỌC THỰC HÀNH SÀI GÒN ĐỀ KIỂM TRA HỌC KỲ I ĐÁP ÁN ĐỀ CHÍNH THỨC NĂM HỌC: 2019 - 2020 MÔN: TOÁN - LỚP: 12 (Đáp án có 03 trang)
Thời gian làm bài: 90 phút
(không kể thời gian phát đề)
PHẦN TRẮC NGHIỆM: 6,0 ĐIỂM CÂU MÃ ĐỀ 101 MÃ ĐỀ 102 MÃ ĐỀ 103 MÃ ĐỀ 104 1 A D B B 2 C A C D 3 A B A C 4 A D D B 5 C B C C 6 B B A D 7 D C D D 8 A C B D 9 B D C A 10 C D D C 11 D B C A 12 D A B A 13 B A D B 14 A D B C 15 B A C C 16 A C D B 17 A C B A 18 C A A A 19 D B A C 20 A C D D 21 C C A B 22 D A D A 23 C D B D 24 D B A B 25 B A C C 26 A C C D 27 B B B D 28 C B A A 29 B D A A 30 D A A B
PHẦN TỰ LUẬN: 4,0 ĐIỂM Đáp án Điểm
Câu 31: Tìm giá trị cực tiểu C y T của hàm số 4 2 y  x  2x  3. x  0  y  3  Ta có: 3 y ' 4x 4x 0 4x  2x 1 0     
   x  1  y  4  x  1  y  4  0,25 x 2 
Từ đó suy ra hàm số đạt cực tiểu tại x  1  và C y T  4  . Trang 1/2
Câu 32: Tìm giá trị lớn nhất của hàm số 3 2
y  2x  3x  12x  2 trên đoạn 1;2   .  x  Ta có 2 1
y  6x  6x 12;y  0   . x  2  0,25  y 1    15; y1  5
 ; y2  6. max y  15 . x1;2 0,25  
Câu 33: Tìm m để đường thẳng y  m cắt đồ thị hàm số 4 2
y  x  2x  2 tại bốn điểm phân biệt. Xét hàm số 4 2 y  x  2x  2  x  0  y  2 3
y  4x  4x, cho y  0   x  1  y  1  -∞ - 1 0 1 +∞ x 0,25 _ y' 0 + 0 _ 0 + + ∞ + ∞ 2 y 1 1
ng thẳng y  m cắt đồ thị hàm số tại 4 điểm phân biệt thì 1  m  2. 0,25
Câu 34: Giải bất phương trình log 3x  5  log x  1 . 1   1   5 5    5 3x  5  0   x  5 BPT     3   x  3 3x  5  x  1  3 0,25 x 2  x  3  Câu 35: Phương trình log x
4 3.2  1  x  1 có hai nghiệm x1, x2 . Tính tổng x1  x2 . PT x x      x 2 1 1 3.2 1 4 2
 3.2x  1  0  2x  6  4 2 . 0,25 4
Vậy x  log2 6  4 2. Ta có x1  x2  2 0,25
Câu 36: Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  a, BC  2a, cạnh bên
SA vuông góc với đáy và SA  a 2 . Tính thể tích khối chóp S.ABCD.       3 1 1 2 2 . .2 . 2 a V Sh a a a  0,25 x 2 3 3 3
Câu 37: Cho hình trụ có diện tích xung quanh bằng 50 và có độ dài đường sinh bằng đường kính
của đường tròn đáy. Tính bán kính r của đường tròn đáy. 2 5 2 Sxq  2 r  l  2 r  .2r  4 r   50  r  0,25 x 2 2
Câu 38: Cho hình nón có bán kính đáy bằng a và độ dài đường sinh bằng 2a . Tính diện tích xung quanh của hình nón đó. 2 x S q  R  l  .  . a 2a  2 a  0,25 x 2
Ghi chú: Học sinh giải cách khác đúng cho đủ điểm tương ứng theo từng phần. Trang 2/2