


Preview text:
TRƯỜNG THPT TÂY THẠNH
Câu 9: Cho lăng trụ đứng ABC.AB C
có đáy là tam giác ABC vuông tại B ; AB 2a , BC a ,
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
AA 2a 3 . Thể tích khối lăng trụ ABC.AB C bằng MÔN TOÁN – KHỐI 12 3 2a 3 3 4a 3
PHẦN TRẮC NGHIỆM (6 điểm) A. 3 4a 3 . B. 3 2a 3 . C. . D. . 3 3
Thời gian làm bài: 60 phút
(Không kể thời gian phát đề) MÃ ĐỀ 911 Câu 10: Cho log 3 .
a Tính giá trị biểu thức P log 9000 theo a A. 2 P a 3. B. 2 P a . C. 2 P 3a . D. P 3 2 . a
Họ và tên học sinh: ………………………………………………………… Lớp:……… Mã số: ……….
Câu 11: Tập xác định D của hàm số y log 2 x 2x là 2 A. D 0; . B. D ; 0 2;. Câu 1: Cho hàm số 4 2
y 3x 4x . Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số đạt cực đại tại gốc tọa độ. C. D ; 02; . D. D ; 0 2; .
B. Hàm số đạt cực tiểu tại gốc tọa độ.
C. Hàm số không có cực trị.
Câu 12: Số nghiệm của phương trình log x 3 log x 2 1 log5 là D. Điểm M 1;
1 là điểm cực tiểu của đồ thị hàm số. A. 0. B. 3. C. 2. D. 1. Câu 2: Hàm số 3 2
y 2x 9x 12x 5 có mấy điểm cực trị ?
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , SA vuông góc với đáy. Biết SC A. 1. B. 2. C. 3. D. 4.
tạo với mặt phẳng ABCD một góc 45 . Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD . sin x 1 A. 2 S 4 a . B. 2 S 6 a . C. 2 S 8 a . D. 2 S 12 a . Câu 3: Kí hiệu ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y . Tính giá 2 sin x sin x 1 x
Câu 14: Tìm tập nghiệm S của bất phương trình 1 3 1 4 2 3
trị biểu thức d 3M – m . A. d 3. B. d 4 . C. d 5. D. d 2 . A. S 1; . B. S 1; . C. S ; 1 . D. S ; 1 . 3 x
Câu 15: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt phẳng Câu 4: Cho hàm số 2 y
3x 5x 2 . Hỏi hàm số nghịch biến trên khoảng nào ? 3
ABC, SB 2a . Tính thể tích khối chóp S.ABC . A. 2;3. B. 1;6 . C. ; 1 . D. (5; ) . 3 a 3 a 3 3 3a 3 a 3 A. . B. . C. . D. . 4 6 4 2
Câu 5: Một hình trụ có chiều cao bằng 3 , chu vi đáy bằng 4 . Tính thể tích của khối trụ. A. 18 . B. 10 . C. 12 . D. 40 .
Câu 16: Hàm số y x 13 1 có đạo hàm là: 1 1 3 2 (x 1) 3 (x 1) x 2 A. y . B. y . C. y . D. y . Câu 6: Cho hàm số y
. Số đường tiệm cận của đồ thị hàm số là 3 2 3 (x 1) 3 3 (x 1) 3 3 2 x 9 A. 3. B. 2. C. 1. D. 4.
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy, mặt bên
SBC tạo với đáy một góc bằng 60 . Gọi M, N lần lượt là trung điểm của SB và SC . Tính thể tích
Câu 7: Số giao điểm của đồ thị hàm số y x 2
1 x 3x 2 với trục Ox là V của khối chóp S.AMN . 3 3 3 3 A. 2 . B. 1 . C. 3 . D. 0. a a a 3 a 3 A. V . B. V . C. V . D. V . 2 4 32 8 1 0,75 1
Câu 8: Giá trị của biểu thức 0,5 4 M 81 36 bằng
Câu 18: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hai hàm số 3 2
y x 2x mx 2 và 16 2
y x m cắt nhau tại một điểm duy nhất. A. 7. B. 5. C. 6. D. 8. A. m 3 . B. m 3 . C. m 3 . D. m 3 . MÃ ĐỀ 911
Toán 12 – HK1 – Trang 1/2 TRƯỜNG THPT TÂY THẠNH
Câu 9: Cho lăng trụ đứng ABC.AB C
có đáy là tam giác ABC vuông tại B ; AB 2a , BC a ,
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020
AA 2a 3 . Thể tích khối lăng trụ ABC.AB C bằng MÔN TOÁN – KHỐI 12 3 2a 3 3 4a 3
PHẦN TRẮC NGHIỆM (6 điểm) A. 3 4a 3 . B. 3 2a 3 . C. . D. . 3 3
Thời gian làm bài: 60 phút
(Không kể thời gian phát đề) MÃ ĐỀ 911 Câu 10: Cho log 3 .
a Tính giá trị biểu thức P log 9000 theo a A. 2 P a 3. B. 2 P a . C. 2 P 3a . D. P 3 2 . a
Họ và tên học sinh: ………………………………………………………… Lớp:……… Mã số: ……….
Câu 11: Tập xác định D của hàm số y log 2 x 2x là 2 A. D 0; . B. D ; 0 2;. Câu 1: Cho hàm số 4 2
y 3x 4x . Khẳng định nào sau đây đúng ?
A. Đồ thị hàm số đạt cực đại tại gốc tọa độ. C. D ; 02; . D. D ; 0 2; .
B. Hàm số đạt cực tiểu tại gốc tọa độ.
C. Hàm số không có cực trị.
Câu 12: Số nghiệm của phương trình log x 3 log x 2 1 log5 là D. Điểm M 1;
1 là điểm cực tiểu của đồ thị hàm số. A. 0. B. 3. C. 2. D. 1. Câu 2: Hàm số 3 2
y 2x 9x 12x 5 có mấy điểm cực trị ?
Câu 13: Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a , SA vuông góc với đáy. Biết SC A. 1. B. 2. C. 3. D. 4.
tạo với mặt phẳng ABCD một góc 45 . Tính diện tích S của mặt cầu ngoại tiếp hình chóp S.ABCD . sin x 1 A. 2 S 4 a . B. 2 S 6 a . C. 2 S 8 a . D. 2 S 12 a . Câu 3: Kí hiệu ,
m M lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hàm số y . Tính giá 2 sin x sin x 1 x
Câu 14: Tìm tập nghiệm S của bất phương trình 1 3 1 4 2 3
trị biểu thức d 3M – m . A. d 3. B. d 4 . C. d 5. D. d 2 . A. S 1; . B. S 1; . C. S ; 1 . D. S ; 1 . 3 x
Câu 15: Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , cạnh bên SB vuông góc với mặt phẳng Câu 4: Cho hàm số 2 y
3x 5x 2 . Hỏi hàm số nghịch biến trên khoảng nào ? 3
ABC, SB 2a . Tính thể tích khối chóp S.ABC . A. 2;3. B. 1;6 . C. ; 1 . D. (5; ) . 3 a 3 a 3 3 3a 3 a 3 A. . B. . C. . D. . 4 6 4 2
Câu 5: Một hình trụ có chiều cao bằng 3 , chu vi đáy bằng 4 . Tính thể tích của khối trụ. A. 18 . B. 10 . C. 12 . D. 40 .
Câu 16: Hàm số y x 13 1 có đạo hàm là: 1 1 3 2 (x 1) 3 (x 1) x 2 A. y . B. y . C. y . D. y . Câu 6: Cho hàm số y
. Số đường tiệm cận của đồ thị hàm số là 3 2 3 (x 1) 3 3 (x 1) 3 3 2 x 9 A. 3. B. 2. C. 1. D. 4.
Câu 17: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , cạnh bên SA vuông góc với đáy, mặt bên
SBC tạo với đáy một góc bằng 60 . Gọi M, N lần lượt là trung điểm của SB và SC . Tính thể tích
Câu 7: Số giao điểm của đồ thị hàm số y x 2
1 x 3x 2 với trục Ox là V của khối chóp S.AMN . 3 3 3 3 A. 2 . B. 1 . C. 3 . D. 0. a a a 3 a 3 A. V . B. V . C. V . D. V . 2 4 32 8 1 0,75 1
Câu 8: Giá trị của biểu thức 0,5 4 M 81 36 bằng
Câu 18: Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hai hàm số 3 2
y x 2x mx 2 và 16 2
y x m cắt nhau tại một điểm duy nhất. A. 7. B. 5. C. 6. D. 8. A. m 3 . B. m 3 . C. m 3 . D. m 3 . MÃ ĐỀ 911
Toán 12 – HK1 – Trang 1/2 3 mx
Câu 26: Giả sử ta có hệ thức 2 2
a b 7ab, (a, b 0). Hệ thức nào sau đây là đúng ?
Câu 19: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2 y f (x)
7mx 14x m 2 giảm 3 a b
A. 2log (a b) log a log . b B. 2log log a log . b
trên nửa khoảng 1; . 2 2 2 2 2 2 3 14 14 14 14 a b a b A. ; C. log 2(log a log b). D. 4log log a log . b . B. ; . C. 2; . D. ; . 2 2 2 2 2 2 15 15 15 15 3 6
Câu 20: Tính diện tích mặt cầu ngoại tiếp một hình lăng trụ tam giác đều có các cạnh đều bằng a . Câu 27: Cho hàm số 4 2
y x (2m 1)x 2m có đồ thị (C) . Giá trị m để đường thẳng: (d) : y 2 cắt đồ thị 2 7 a 2 7 a 2 7 a 2 3 a
(C) tại bốn điểm phân biệt đều có hoành độ nhỏ hơn 3 là A. . B. . C. . D. . 3 6 5 7 3 m 3 m 11 A. 2 . B. 2 . C. 1 m . D. 1 m 2 . 11 2
Câu 21: Cho tứ diện đều ABCD có cạnh bằng a . Hình nón N có đỉnh A và đường tròn đáy là đường tròn 1 m 1 m 2 2
ngoại tiếp tam giác BCD . Tính thể tích V của khối nón N . 3 3a 3 6a 3 6a 3 6a A. V . B. V . C. V . D. V . ax 1
Câu 28: Xác định a,b để hàm số y
có đồ thị như hình vẽ bên. y 27 27 9 27 x b Chọn khẳng định đúng
Câu 22: Cho hình chóp S.ABCD , đáy ABCD là hình vuông có cạnh bằng 2a . Tam giác SAB cân tại S và A. a 1, b 1.
nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa SC và mặt đáy bằng 60 . Tính khoảng cách h B. a 1, b 1. 1
giữa hai đường thẳng BD và SA . C. a 1, b 1. -2 -1 1 x a 11 2a 66 a 15 2a 15 A. h . B. h . C. h . D. h . D. a 1, b 1. 11 11 31 31
Câu 23: Tìm tham số m để phương trình 4x 2 1 .2x m
3m 8 0 có hai nghiệm trái dấu.
Câu 29: Giá trị của tham số m để hàm số 3 2
f (x) x 3x mx 1 có hai điểm cực trị x , x thỏa mãn 1 2 8 8 2 2 A. 1 m 9. B. m . C. m 9. D. m 9. x x 3 là 1 2 3 3 3 1 A. m 1. B. m 2 . C. m . D. m . 2 2
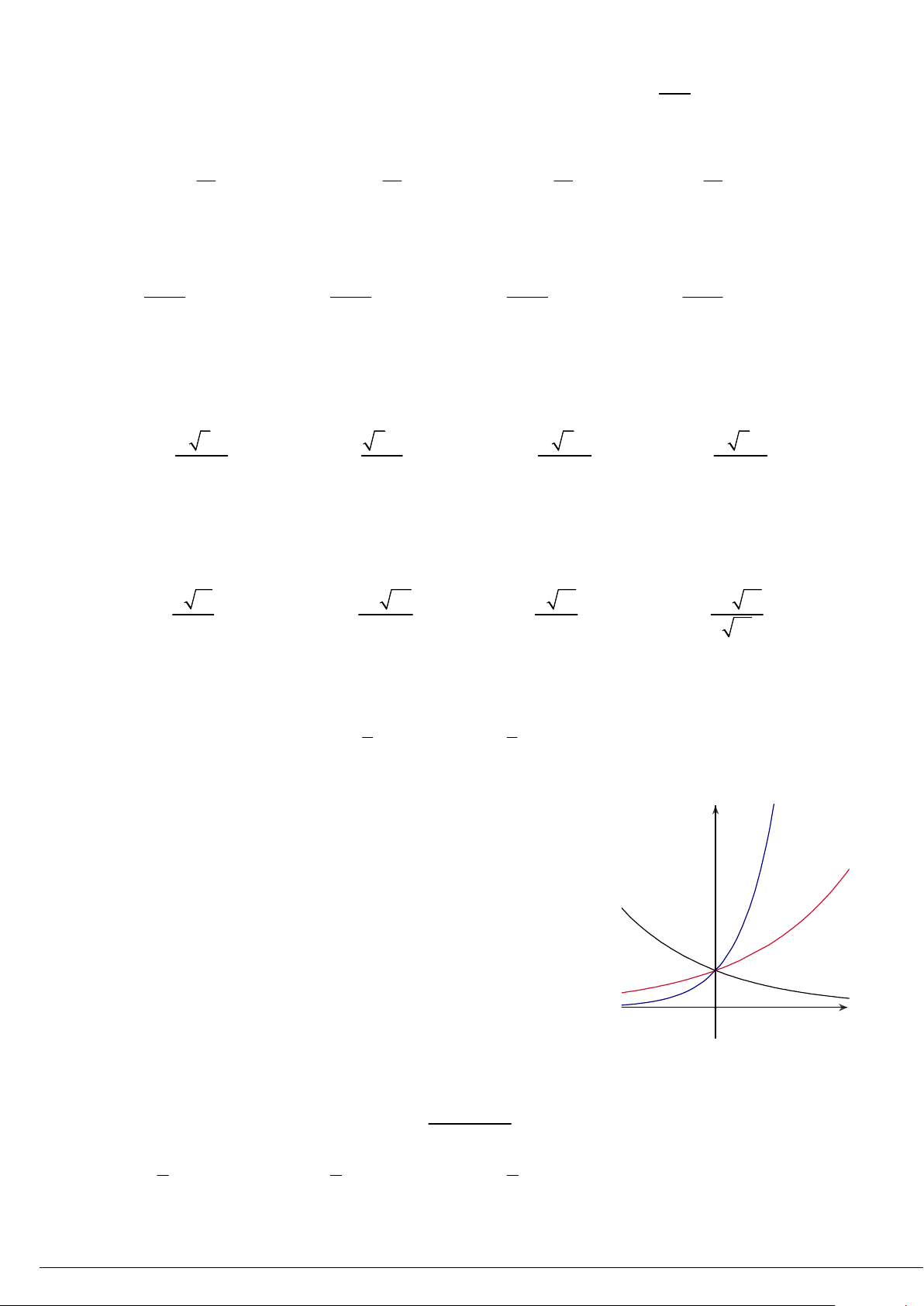
Câu 24: Hình bên là đồ thị của ba hàm số x y a , x y b , y x y c 0 a, , b c
1 được vẽ trên cùng một hệ trục tọa độ. y = bx 500
Câu 30: Người ta cần xây một hồ chứa nước dạng khối hộp chữ nhật không nắp có thể tích bằng m3. Đáy
Khẳng định nào sau đây là khẳng định đúng ? 3 A. b a c .
hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000đồng/m2. y = cx B. a b c
Người ta phải tính toán kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là: y = ax C. a c b . A. 74 triệu đồng. B. 75 triệu đồng. C. 76 triệu đồng. D. 77 triệu đồng. D. c b a .
……………HẾT………….. O x 5 3x 3x
Câu 25: Cho 9x 9x 23 . Khi đó biểu thức K có giá trị bằng 1 3x 3x 5 1 3 A. . B. . C. . D. 2. 2 2 2 MÃ ĐỀ 911
Toán 12 – HK1 – Trang 2/2 3 mx
Câu 26: Giả sử ta có hệ thức 2 2
a b 7ab, (a, b 0). Hệ thức nào sau đây là đúng ?
Câu 19: Tìm tất cả các giá trị thực của tham số m sao cho hàm số 2 y f (x)
7mx 14x m 2 giảm 3 a b
A. 2log (a b) log a log . b B. 2log log a log . b
trên nửa khoảng 1; . 2 2 2 2 2 2 3 14 14 14 14 a b a b A. ; C. log 2(log a log b). D. 4log log a log . b . B. ; . C. 2; . D. ; . 2 2 2 2 2 2 15 15 15 15 3 6
Câu 20: Tính diện tích mặt cầu ngoại tiếp một hình lăng trụ tam giác đều có các cạnh đều bằng a . Câu 27: Cho hàm số 4 2
y x (2m 1)x 2m có đồ thị (C) . Giá trị m để đường thẳng: (d) : y 2 cắt đồ thị 2 7 a 2 7 a 2 7 a 2 3 a
(C) tại bốn điểm phân biệt đều có hoành độ nhỏ hơn 3 là A. . B. . C. . D. . 3 6 5 7 3 m 3 m 11 A. 2 . B. 2 . C. 1 m . D. 1 m 2 . 11 2
Câu 21: Cho tứ diện đều ABCD có cạnh bằng a . Hình nón N có đỉnh A và đường tròn đáy là đường tròn 1 m 1 m 2 2
ngoại tiếp tam giác BCD . Tính thể tích V của khối nón N . 3 3a 3 6a 3 6a 3 6a A. V . B. V . C. V . D. V . ax 1
Câu 28: Xác định a,b để hàm số y
có đồ thị như hình vẽ bên. y 27 27 9 27 x b Chọn khẳng định đúng
Câu 22: Cho hình chóp S.ABCD , đáy ABCD là hình vuông có cạnh bằng 2a . Tam giác SAB cân tại S và A. a 1, b 1.
nằm trong mặt phẳng vuông góc với mặt đáy. Góc giữa SC và mặt đáy bằng 60 . Tính khoảng cách h B. a 1, b 1. 1
giữa hai đường thẳng BD và SA . C. a 1, b 1. -2 -1 1 x a 11 2a 66 a 15 2a 15 A. h . B. h . C. h . D. h . D. a 1, b 1. 11 11 31 31
Câu 23: Tìm tham số m để phương trình 4x 2 1 .2x m
3m 8 0 có hai nghiệm trái dấu.
Câu 29: Giá trị của tham số m để hàm số 3 2
f (x) x 3x mx 1 có hai điểm cực trị x , x thỏa mãn 1 2 8 8 2 2 A. 1 m 9. B. m . C. m 9. D. m 9. x x 3 là 1 2 3 3 3 1 A. m 1. B. m 2 . C. m . D. m . 2 2
Câu 24: Hình bên là đồ thị của ba hàm số x y a , x y b , y x y c 0 a, , b c
1 được vẽ trên cùng một hệ trục tọa độ. y = bx 500
Câu 30: Người ta cần xây một hồ chứa nước dạng khối hộp chữ nhật không nắp có thể tích bằng m3. Đáy
Khẳng định nào sau đây là khẳng định đúng ? 3 A. b a c .
hồ là hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê nhân công để xây hồ là 500.000đồng/m2. y = cx B. a b c
Người ta phải tính toán kích thước của hồ nước sao cho chi phí thuê nhân công thấp nhất. Chi phí đó là: y = ax C. a c b . A. 74 triệu đồng. B. 75 triệu đồng. C. 76 triệu đồng. D. 77 triệu đồng. D. c b a .
……………HẾT………….. O x 5 3x 3x
Câu 25: Cho 9x 9x 23 . Khi đó biểu thức K có giá trị bằng 1 3x 3x 5 1 3 A. . B. . C. . D. 2. 2 2 2 MÃ ĐỀ 911
Toán 12 – HK1 – Trang 2/2 TRƯỜNG THPT TÂY THẠNH
ĐỀ KIỂM TRA HỌC KỲ I – NĂM HỌC 2019-2020 MÔN: TOÁN – KHỐI 12
PHẦN TỰ LUẬN ( 4 điểm)
Thời gian làm bài: 30 phút
(Không kể thời gian phát đề)
Họ và tên học sinh: …………………………………………………………Lớp:………Mã số: ………
Câu 1. (1.0 điểm): Khảo sát sự biến thiên và cực trị của hàm số : 4 2 y x 2x 2
Câu 2. (1.0 điểm): Giải phương trình : 3 log x log 3x 1 0 3 3
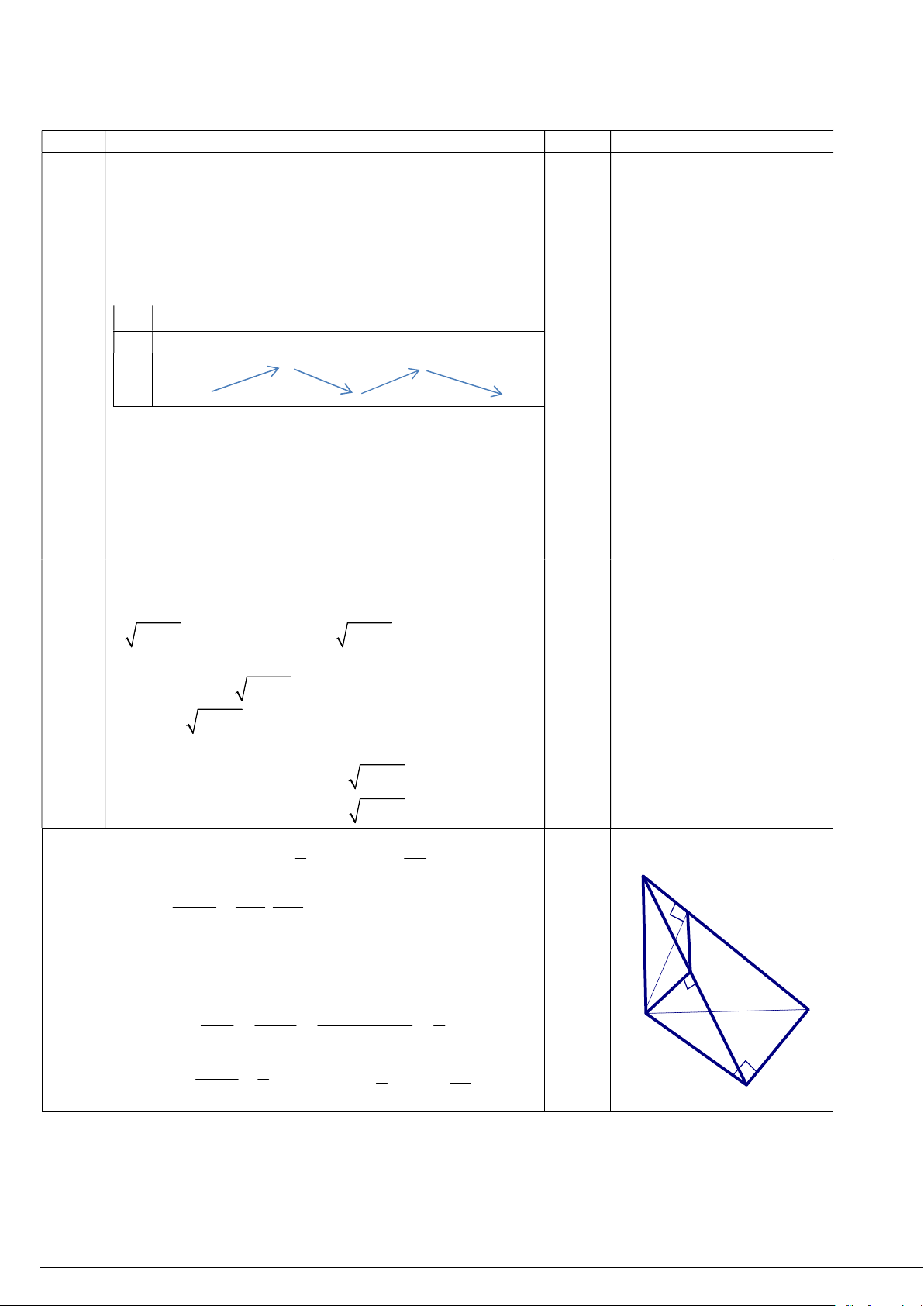
Câu 3. (1.0 điểm): Cho tứ diện ABCD có ABC là tam giác vuông cân tại A và DC vuông góc với mặt
phẳng ABC .Gọi E, F lần lượt là hình chiếu của C lên cạnh AD và BD . Biết AB CD a . Tính
thể tích khối tứ diện CDEF .
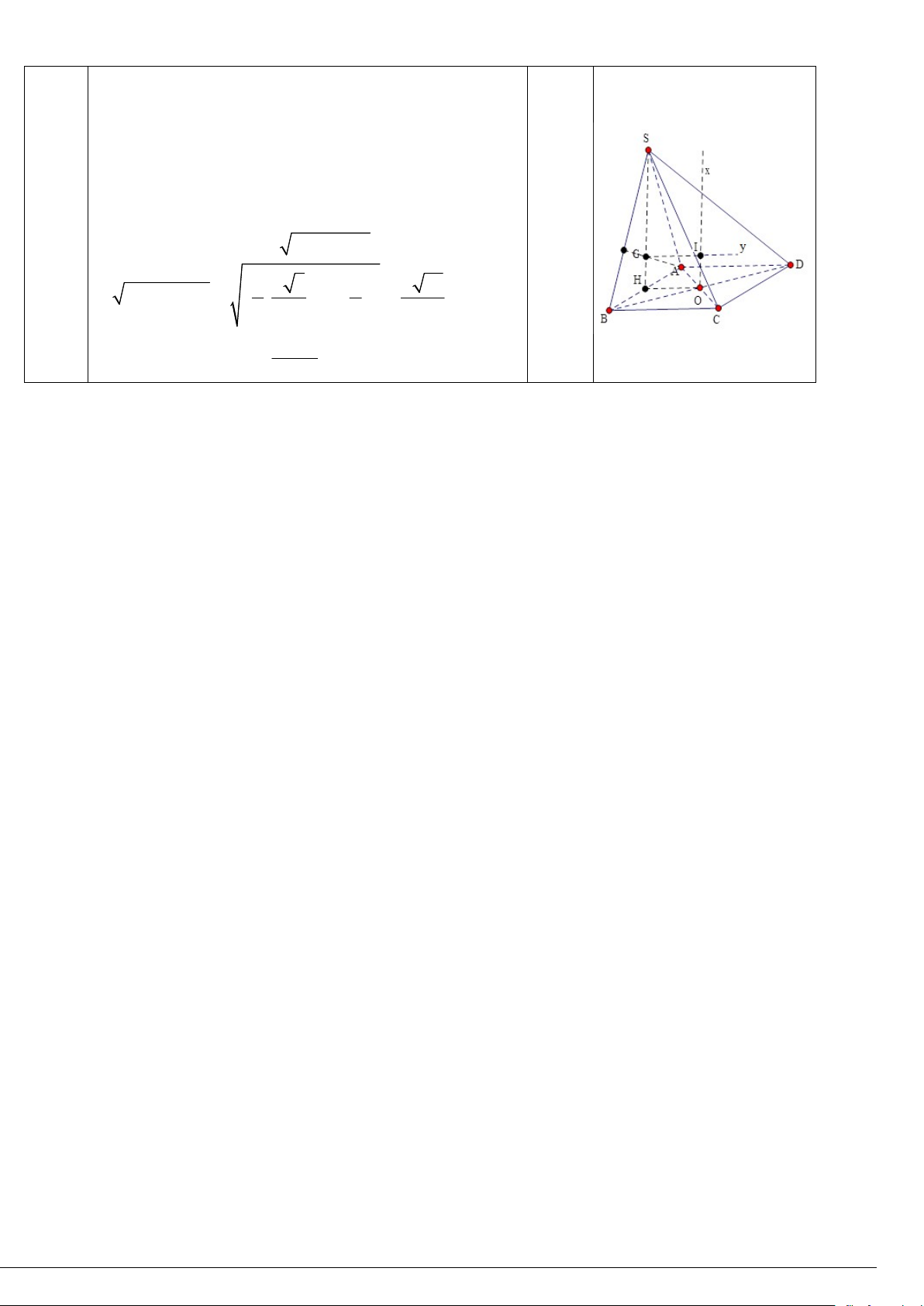
Câu 4. (1.0 điểm) : Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , tam giác SAB là tam giác
đều. Gọi H là trung điểm AB và là chân đường cao hình chóp S.ABCD . Xác định tâm mặt cầu S
ngoại tiếp hình chóp SABCD và tính diện tích mặt cầu S . -------Hết------ MÃ ĐỀ 911
Toán 12 – HK1 – Trang 3/2
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I - NĂM HỌC 2019-2020
Gọi O AC BD , dựng Ox ABCD Ox//SH .
PHẦN TỰ LUẬN – MÔN TOÁN - KHỐI 12
Gọi G là trọng tâm tam giác đều SAB . Dựng 0,25 Câu
Lời giải (cần vắn tắt – rõ các bước được điểm) Điểm Lưu ý khi chấm
Gy SAB Gy//HO , Gy Ox I . ' 3
Tap xac dinh D R ; y 4x 4x
I Ox IA IB IC 0,25 Ta có
suy ra I là tâm mặt cầu 0,25 x 0 y 2
I Gy IS IA IB Câu
ngoại tiếp hình chóp S.ABCD . '
y 0 x 1 y 1 4 x 1 y 1 0,25 Bán kính mặt cầu : 2 2 SI SG GI 2 2 lim y ; lim y 2 a 3 a a 21 x x 2 2 SG HO . . Câu x -1 0 1 3 2 2 6 0,25 1 y’ + 0 - 0 + 0 - 2 7 a y -1 -1
Diện tích mặt cầu : S 0,25 3 -2 0,25 HS dong bientren ( ; 1);(0;1)
HS nghichbientren (1;0);(1; ) HS dat cuc dai tai x 1 ; y 1 CD
HS dat cuc dai tai x 1; y 1 CD
HS dat cuc tieu tai x 0; y 2 0,25 CT x 0 x 0 0,25 Điều kiện: x 1 log x 0 x 1 3
3 log x log 3x 1 0 3 log x 1 log x 1 0 3 3 3 3 Câu 2 0,25 log x 3 log x 2 0 3 3 Đặt t log x t 0 3 Ta có 0,25 t 1 log x 1 3 x 3 2 t 3t 2 0 t 2 log x 2 x 81 0,25 3 V 3 1 a Tính ABCD : V S .CD ABCD 3 ABC 6 0,25 D V DE DF DCEF . (*) F Ta có: V DA DB DABC a 2 2 DE DC a 1 Câu 0,25 E 2 2 3 DA DA 2a 2 B 2 2 DF DC a 1 0,25 C 2 2 2 DB DB DC CB 3 Tương tự: a V 1 3 DCEF 1 a V V 0,25 A DCEF ABCD Từ (*) V 6 DABC .Vậy 6 36 MÃ ĐỀ 911
Toán 12 – HK1 – Trang 4/2
HƯỚNG DẪN CHẤM KIỂM TRA HỌC KỲ I - NĂM HỌC 2019-2020
Gọi O AC BD , dựng Ox ABCD Ox//SH .
PHẦN TỰ LUẬN – MÔN TOÁN - KHỐI 12
Gọi G là trọng tâm tam giác đều SAB . Dựng 0,25 Câu
Lời giải (cần vắn tắt – rõ các bước được điểm) Điểm Lưu ý khi chấm
Gy SAB Gy//HO , Gy Ox I . ' 3
Tap xac dinh D R ; y 4x 4x
I Ox IA IB IC 0,25 Ta có
suy ra I là tâm mặt cầu 0,25 x 0 y 2
I Gy IS IA IB Câu
ngoại tiếp hình chóp S.ABCD . '
y 0 x 1 y 1 4 x 1 y 1 0,25 Bán kính mặt cầu : 2 2 SI SG GI 2 2 lim y ; lim y 2 a 3 a a 21 x x 2 2 SG HO . . Câu x -1 0 1 3 2 2 6 0,25 1 y’ + 0 - 0 + 0 - 2 7 a y -1 -1
Diện tích mặt cầu : S 0,25 3 -2 0,25 HS dong bientren ( ; 1);(0;1)
HS nghichbientren (1;0);(1; ) HS dat cuc dai tai x 1 ; y 1 CD
HS dat cuc dai tai x 1; y 1 CD
HS dat cuc tieu tai x 0; y 2 0,25 CT x 0 x 0 0,25 Điều kiện: x 1 log x 0 x 1 3
3 log x log 3x 1 0 3 log x 1 log x 1 0 3 3 3 3 Câu 2 0,25 log x 3 log x 2 0 3 3 Đặt t log x t 0 3 Ta có 0,25 t 1 log x 1 3 x 3 2 t 3t 2 0 t 2 log x 2 x 81 0,25 3 V 3 1 a Tính ABCD : V S .CD ABCD 3 ABC 6 0,25 D V DE DF DCEF . (*) F Ta có: V DA DB DABC a 2 2 DE DC a 1 Câu 0,25 E 2 2 3 DA DA 2a 2 B 2 2 DF DC a 1 0,25 C 2 2 2 DB DB DC CB 3 Tương tự: a V 1 3 DCEF 1 a V V 0,25 A DCEF ABCD Từ (*) V 6 DABC .Vậy 6 36 MÃ ĐỀ 911
Toán 12 – HK1 – Trang 4/2




