

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO ĐỀ KIỂM TRA HỌC KỲ I
THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2019 – 2020
TRƯỜNG THPT TRẦN VĂN GIÀU MÔN TOÁN LỚP 12 – BAN CƠ BẢN Thời gian: 90 phút
Họ tên học sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .SBD: . . . . . . . . .Lớp: 12A . . . Mã đề: 111 I. TRẮC NGHIỆM Câu 1. Tập xác định của hàm số . A. . B. . C. . D. .
Câu 2. Kí hiệu và lần lượt là tập nghiệm của các phương trình và
. Khi đó khẳng định đúng là A. . B. . C. . D. .
Câu 3. Giá trị cực tiểu của hàm số là A. . B. . C. . D. .
Câu 4. Tìm tập nghiệm của phương trình ? A. . B. . C. . D. .
Câu 5. Tìm tập nghiệm của bất phương trình A. B. C. D.
Câu 6. Tìm giá trị của tham số m để hàm số nghịch biến trên ? A. . B. . C. . D. .
Câu 7. Tìm giá trị nhỏ nhất m của hàm số trên đoạn . A. . B. . C. . D. . Câu 8. Cho hàm số . Tính bằng A. . B. . C. . D. .
Câu 9. Tìm tập nghiệm S của phương trình . A. S = . B. S = . C. S = . D. S = .
Câu 10. Tìm tập xác định D của hàm số ? A. B. C. D.
Câu 11. Hàm số nào trong các hàm số sau nghịch biến trên . A. . B. . C. . D. . Câu 12. Tìm để phương trình có nghiệm. A. . B. hoặc . C. . D. . Trang 1/5- Mã Đề 111
Câu 13. Đồ thị hàm số nào sau đây cắt trục tung tại điểm có tung độ bằng 1. A. B. C. D.
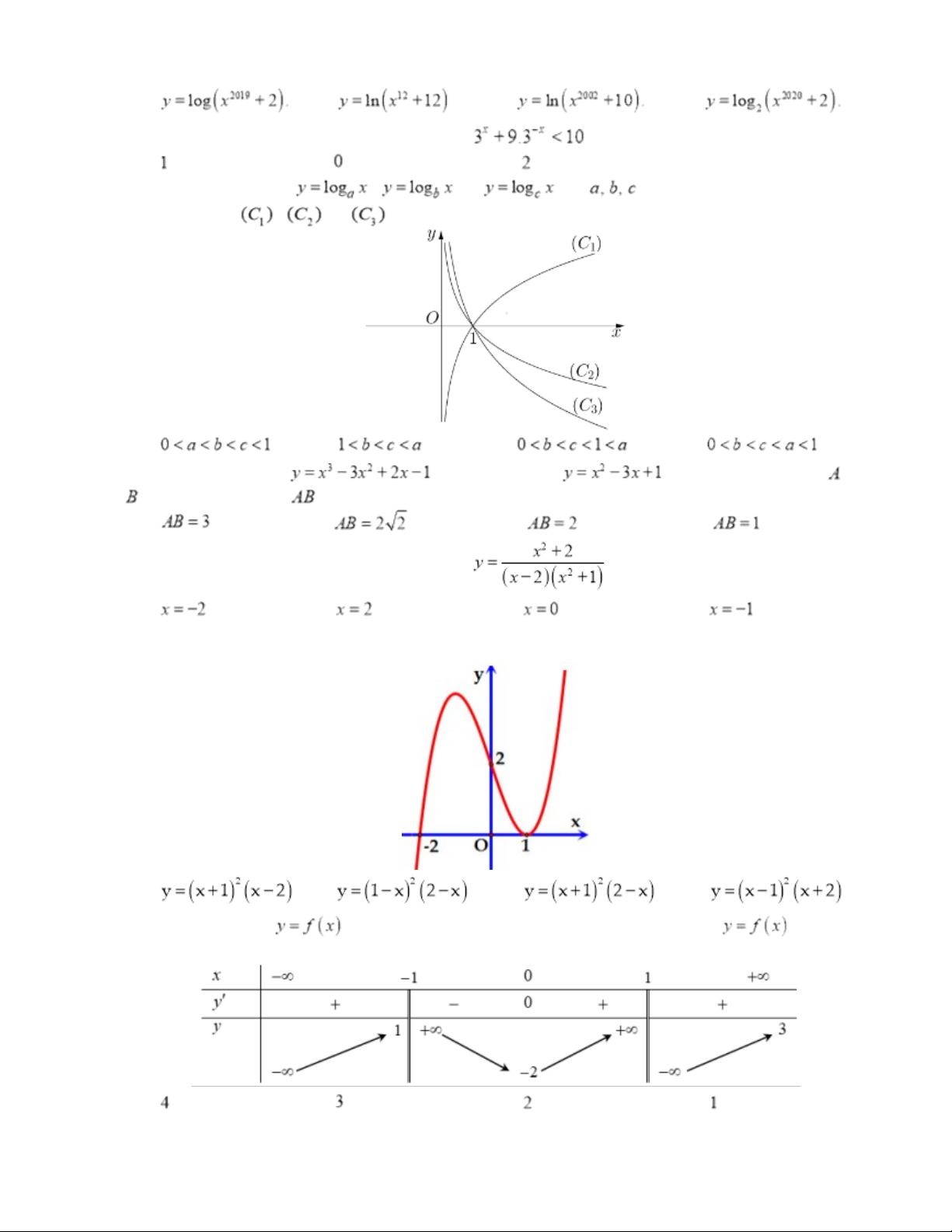
Câu 14. Số nghiệm nguyên của bất phương trình là A. . B. . C. . D. Vô số. Câu 15. Cho ba hàm số , và với
là ba số thực dương khác 1, lần lượt có đồ thị là , và
như hình vẽ sau. Mệnh đề nào sau đây đúng? A. . B. . C. . D. .
Câu 16. Đồ thị hàm số cắt đồ thị hàm số
tại hai điểm phân biệt và . Khi đó độ dài đoạn là bao nhiêu? A. . B. . C. . D. .
Câu 17. Đường tiệm cận đứng của đồ thị hàm số là A. . B. . C. . D. .
Câu 18. Đường cong trong hình bên là đồ thị của một hàm số trong bốn hàm số được liệt kê ở bốn
phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào? A. B. C. D. Câu 19. Cho hàm số
có bảng biến thiên như hình dưới. Hỏi đồ thị hàm số có bao
nhiêu đường tiệm cận? A. . B. . C. . D. . Trang 2/5- Mã Đề 111 Câu 20. Cho hàm số
. Tìm tất cả các giá trị thực của để đồ thị hàm số có hai
điểm cực trị , sao cho ba điểm , , thẳng hàng, trong đó là gốc tọa độ? A. B. C. D. Câu 21. Cho tam giác vuông tại có , , quay tam giác xung quanh cạnh
được hình nón. Thể tích của khối nón tương ứng là: A. . B. . C. . D. . Câu 22. Cho hàm số
. Tính tổng các giá trị của tham số m sao cho giá trị nhỏ nhất của hàm số trên bằng là A. 0 B. 2 C. -2 D. 1
Câu 23. Cho khối lăng trụ có đáy là hình vuông cạnh a và chiều cao bằng 4a. Thể tích của khối lăng trụ đã cho bằng 16 4 A. 3 4a B. 3 a C. 3 a D. 3 16a 3 3 Câu 24. Cho hình chóp
có đáy là hình vuông cạnh , cạnh
vuông góc với mặt đáy, góc giữa đường thẳng và mặt phẳng là . Gọi sao cho . Tính tỉ số thể tích A. . B. . C. . D. .
Câu 25. Cho hình chóp S.ABC có
và đôi một vuông góc. Diện tích mặt cầu ngoại tiếp hình chóp S.ABC. A. B. C. D.
Câu 26. Cho hình lăng trụ đứng
có đáy là hình thoi, biết , , .
Thể tích của khối lăng trụ là A. . B. . C. . D. .
Câu 27. Bán kính mặt cầu ngoại tiếp lăng trụ tam giác đều có cạnh đáy bằng , cạnh bên bằng là A. B. C. D.
Câu 28. Cho khối chóp tam giác đều. Nếu tăng cạnh đáy lên hai lần và giảm chiều cao đi 4 lần thì thể tích
của khối chóp đó sẽ thay đổi như thế nào? A. Tăng lên hai lần. B. Giảm đi ba lần. C. Giảm đi hai lần. D. Không thay đổi.
Câu 29. Cho một khối trụ có độ dài đường sinh bằng 10, biết thể tích của khối trụ bằng . Diện tích
xung quanh của khối trụ là: A. . B. . C. . D. .
Câu 30. Cho hình nón có góc ở đỉnh bằng
diện tích xung quanh bằng . Tính thể tích của khối nón đã cho. A. . B. . C. . D. . Trang 3/5- Mã Đề 111 Câu 31. Xét hàm số
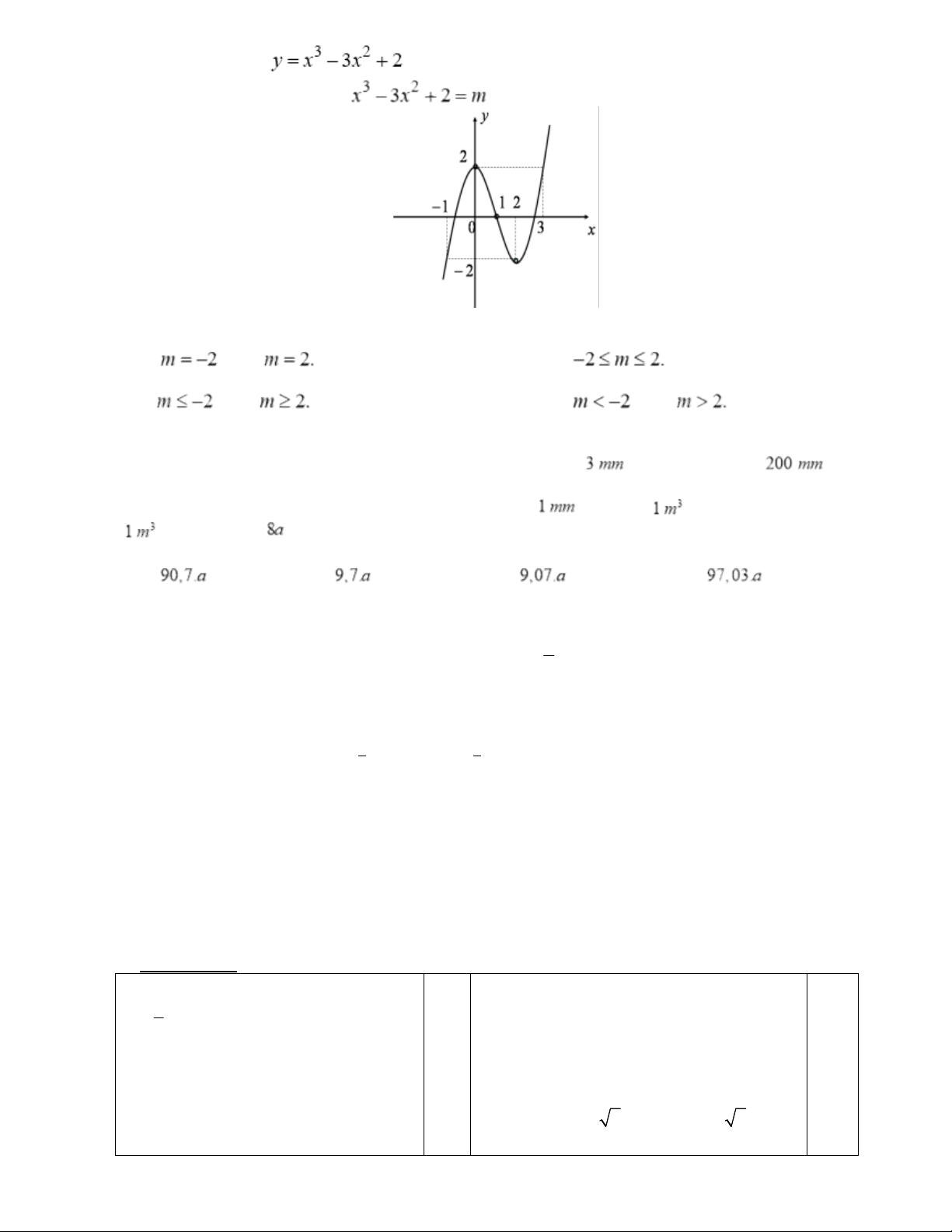
có đồ thị (C) được cho ở hình bên. Tìm tất cả các giá trị của tham
số thực m sao cho phương trình
có 2 nghiệm thực phân biệt. A. hoặc B. C. hoặc D. hoặc
Câu 32. Một chiếc bút chì khối lăng trụ lục giác đều có cạnh đáy và chiều cao bằng .
Thân bút chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng khối trụ có chiều
cao bằng chiều dài của bút chì và đáy là hình tròn bán kính . Giả định
gỗ có giá a (triệu đồng), than chì có giá
(triệu đồng). Khi đó giá nguyên vật liệu làm một chiếc bút chì như trên gần nhất
với kết quả nào sau đây? A. (đồng). B. (đồng). C. (đồng). D. (đồng). II. TỰ LUẬN 1
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số 3 2 y x mx 2
m 4x 9 đạt cực đại tại 3 x 3.
Câu 2. Tìm tất cả các giá trị của tham số m để đồ thị hàm số 4 2
y x 2x m cắt trục hoành tại 4 điểm. 2
Câu 3. Giải bất phương trình log x 3x log x 4 4 4
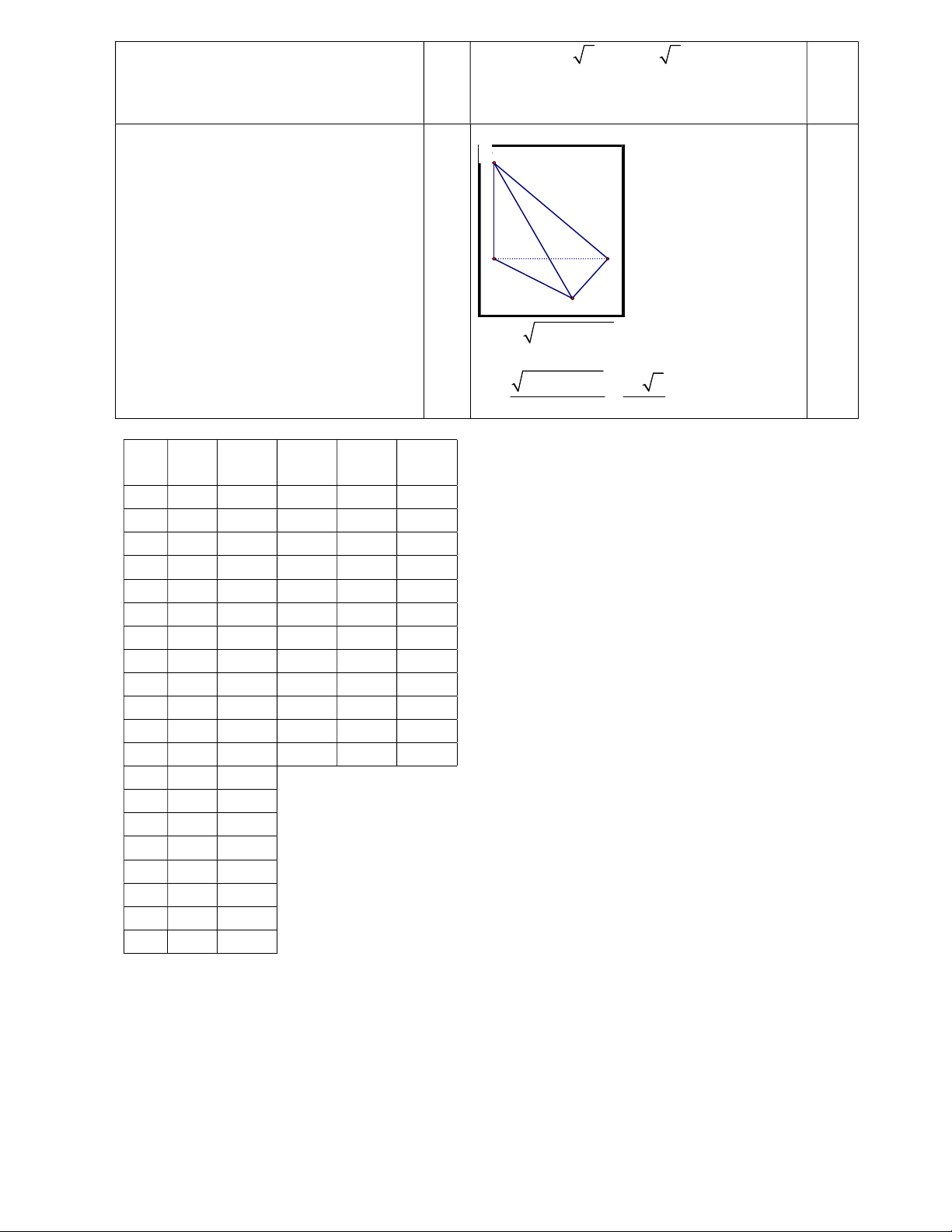
Câu 4. Cho tứ diện DABC , đáy ABC là tam giác vuông tại B, DA vuông góc với mặt đáy. Biết
AB = 3a, BC = 4a, DA =5a . Tìm bán kính mặt cầu ngoại tiếp hình chóp DABC. ---------- HẾT ----------
ĐÁP ÁN ĐỀ THI HỌC KỲ I MÔN TOÁN LỚP 12 Năm học 2019 - 2020 B.Phần tự luận Câu 1: Câu 3: 1 2 3 2 2
y x mx (m 4)x 9 x 3x 0 x 0 hay x 3 3 ĐK: x 4 0 x 4 2 2 y ' x 2mx m 4 4 x 0 hay x 3 y ' 2x m 2 x 3x x 4 y '(3) 0 BPT ycbt
x 2 2 2 hay x 2 2 2 y '(3) 0 0,25 0,25
So với điều kiện ta có tập nghiệm Trang 4/5- Mã Đề 111 m 1 (l)
S (4; 2 2 2) (2 2 2; ) 0,25 m 5 (n) 0,25 m 3 Câu 2: Câu 4: 4 2
ycbt x 2x m có 4 nghiệm phân S D biệt. Đặt 4 2 f (x) x 2x x 0 y 0 3 f '(x) 4x 4x 0 0,25 A C x 1 y 1 Suy ra: 0 m 1 0,25 B 2 2 AC AB BC 5a 0,25
Bán kính mặt cầu ngoại tiếp hình chóp là 2 2 DA AC 5a 2 R 0,25 2 2 Ma Cau Dap Ma Cau Dap de an de an 111 1 A 111 21 D 111 2 D 111 22 D 111 3 D 111 23 A 111 4 B 111 24 D 111 5 A 111 25 D 111 6 B 111 26 B 111 7 B 111 27 B 111 8 A 111 28 D 111 9 B 111 29 A 111 10 A 111 30 A 111 11 C 111 31 A 111 12 C 111 32 C 111 13 D 111 14 A 111 15 C 111 16 D 111 17 B 111 18 D 111 19 B 111 20 D Trang 5/5- Mã Đề 111




