Đề thi học kì 1 Toán 6 Kết nối tri thức năm 2023 - 2024 Đề 4

BẢN ĐẶC TẢ MA TRẬN ĐỀ KIỂM TRA CUỐI KÌ I MÔN TOÁN -LỚP 6 TT Chủ đề
Mức độ đánh giá
Số câu hỏi theo mức độ nhận thức Nhận Thông Vận Vận biêt hiểu dụng dụng cao SỐ VÀ ĐẠI SỐ
Số tự nhiên và tập 1
hợp các số tự Nhận biết: (TN1)
nhiên. Thứ tự
– Nhận biết được tập hợp các số tự
trong tập hợp các nhiên.
số tự nhiên
Nhận biết: 1
– Nhận biết được thứ tự thực hiện các (TN2)
phép tính. Vận dụng: TL 1
– Thực hiện được các phép tính: cộng, 13a TL Số tự
trừ, nhân, chia trong tập hợp số tự nhiên. 14b 1 nhiên
Các phép tính với – Vận dụng được các tính chất giao
số tự nhiên. Phép hoán, kết hợp, phân phối của phép nhân
tính luỹ thừa với đối với phép cộng trong tính toán.
số mũ tự nhiên
– Thực hiện được phép tính luỹ thừa với
số mũ tự nhiên; thực hiện được các phép
nhân và phép chia hai luỹ thừa cùng cơ
số với số mũ tự nhiên.
– Vận dụng được các tính chất của phép
tính (kể cả phép tính luỹ thừa với số mũ
tự nhiên) để tính nhẩm, tính nhanh một cách hợp lí.
– Giải quyết được những vấn đề thực
tiễn (đơn giản, quen thuộc) gắn với
thực hiện các phép tính (ví dụ: tính tiền
mua sắm, tính lượng hàng mua được từ
số tiền đã có, ...). Nhận biết : 2
– Nhận biết được quan hệ chia hết, khái (TN3,
niệm ước và bội. TN4)
– Nhận biết được khái niệm số nguyên tố, hợp số. Vận dụng:
– Thực hiện được việc phân tích một số
tự nhiên lớn hơn 1 thành tích của các
Tính chia hết
thừa số nguyên tố trong những trường
trong tập hợp các hợp đơn giản.
số tự nhiên. Số
– Xác định được ước chung, ước chung
nguyên tố. Ước
lớn nhất; xác định được bội chung, bội chung và bội
chung nhỏ nhất của hai hoặc ba số tự chung
nhiên; thực hiện được phép cộng, phép
trừ phân số bằng cách sử dụng ước
chung lớn nhất, bội chung nhỏ nhất.
– Vận dụng được kiến thức số học vào
giải quyết những vấn đề thực tiễn (đơn
giản, quen thuộc) (ví dụ: tính toán tiền
hay lượng hàng hoá khi mua sắm, xác
định số đồ vật cần thiết để sắp xếp
chúng theo những quy tắc cho trước,...). Vận dụng cao: 1
– Vận dụng được kiến thức số học vào TL 15
giải quyết những vấn đề thực tiễn (phức
hợp, không quen thuộc). Nhận biết: 2
Số nguyên âm và – Nhận biết được số nguyên âm, tập hợp TN 5
tập hợp các số các số nguyên. TN6
nguyên. Thứ tự
trong tập hợp các – Nhận biết được ý nghĩa của số nguyên
số nguyên
âm trong một số bài toán thực tiễn. Vận dụng: 1 1
– Thực hiện được các phép tính: cộng, (TL13 (TL
trừ, nhân, chia (chia hết) trong tập hợp b, 14a) 14.2) các số nguyên.
– Vận dụng được các tính chất giao Số
hoán, kết hợp, phân phối của phép nhân 2 nguyên
đối với phép cộng, quy tắc dấu ngoặc
Các phép tính với trong tập hợp các số nguyên trong tính
số nguyên. Tính toán (tính viết và tính nhẩm, tính nhanh
chia hết trong tập một cách hợp lí).
hợp các số nguyên – Giải quyết được những vấn đề thực
tiễn (đơn giản, quen thuộc) gắn với
thực hiện các phép tính về số nguyên
(ví dụ: tính lỗ lãi khi buôn bán,...).
Vận dụng cao: 1
– Giải quyết được những vấn đề thực (TL17)
tiễn (phức hợp, không quen thuộc) gắn
với thực hiện các phép tính về số nguyên.
HÌNH HỌC VÀ ĐO LƯỜNG Nhận biết: 1
Tam giác đều,
– Nhận dạng được tam giác đều, hình (TN7)
hình vuông, lục
vuông, hình chữ nhật, hình thoi, hình
giác đều
bình hành, hình thang cân. lục giác đều. Các Thông hiểu: 1 hình
– Mô tả được một số yếu tố cơ bản (TN 8) phẳng 3
(cạnh, góc, đường chéo) của hình chữ trong
Hình chữ nhật,
nhật, hình thoi, hình bình hành, hình thực
hình thoi, hình thang cân. tiễn
bình hành, hình Vận dụng 1
thang cân
– Giải quyết được một số vấn đề thực TL 16
tiễn gắn với việc tính chu vi và diện tích
của các hình đặc biệt nói trên. Nhận biết: 2
– Nhận biết được trục đối xứng của một (TN9,T
Hình có trục đối hình phẳng. N10) Tính xứng
– Nhận biết được những hình phẳng đối
trong tự nhiên có trục đối xứng (khi xứng
quan sát trên hình ảnh 2 chiều). của Nhận biết: 1 hình 4 phẳng
– Nhận biết được tâm đối xứng của một (TN11)
Hình có tâm đối hình phẳng. trong xứng thế giới
– Nhận biết được những hình phẳng tự
trong thế giới tự nhiên có tâm đối xứng nhiên
(khi quan sát trên hình ảnh 2 chiều).
Vai trò của đối Nhận biết: 1
xứng trong thế
– Nhận biết được tính đối xứng trong (TN12)
giới tự nhiên
Toán học, tự nhiên, nghệ thuật, kiến
trúc, công nghệ chế tạo,...
– Nhận biết được vẻ đẹp của thế giới tự
nhiên biểu hiện qua tính đối xứng (ví dụ:
nhận biết vẻ đẹp của một số loài thực
vật, động vật trong tự nhiên có tâm đối
xứng hoặc có trục đối xứng).
KHUNG MA TRẬN ĐỀ KIỂM TRA CUỐI HỌC KÌ 1 MÔN TOÁN - LỚP 6
Mức độ đánh giá (4-11) Tổng Chươn Vận
Nội dung/đơn vị kiến Nhận biết Thông hiểu Vận dụng Tỉ lệ g/ dụng cao TT thức Chủ đề T T Tổng (3) TN N N TNK điể (2) m TNKQ TL TL TL TL TL KQ K K Q Q Q Số tự nhiên và tập 1 hợp các số tự nhiên. (0,25đ) 2,5% 0,25
Thứ tự trong tập hợp (TN1) các số tự nhiên Các phép tính với số tự nhiên. Phép tính 1 1 1 Số tự (0,25đ) (1,0đ) (1,0đ) 2,5% 20% 2,25 1
luỹ thừa với số mũ tự nhiên (TN2) TL13a TL 14b nhiên Tính chia hết trong tập hợp các số tự 2 (0,5đ) 1
nhiên. Số nguyên tố (0,5đ) 5% 5% 1,0 Ước chung và bội (TN3, TL 15 TN4) chung Số nguyên âm và tập hợp các số nguyên 1 . (0,25đ) 2,5% 0,25
Thứ tự trong tập hợp Số các số nguyên (TN5) 2
nguyên Các phép tính với số 2 1 1 1 nguyên. Tính chia hết (2,0đ) (1,0đ) (0,25đ) (0,5đ) trong tập hợp các số 2,5% 35% 3,75 (TL13b, (TN14.2 (TN6) TL 17 nguyên TL14.1a) ) Các Tam giác đều, hình 1 hình vuông, lục giác đều (0,25đ) 2,5% 0,25 phẳng (TN7) 3 trong Hình chữ nhật, hình 1 1 thực thoi, hình bình hành, (0,25đ) (1,0đ) 2,5% 10% 1,25 tiễn hình thang cân (TN8) TL16 Tính 2 đối (0,5đ) Hình có trục đố i xứng 5% 0,5 xứng (TN9, của TN10) hình 1 4
phẳng Hình có tâm đối xứng (0,25đ) 2,5% 0,25 trong (TN11)
thế giới Vai trò của đối xứng 1 tự trong thế giới tự (0,25đ) 2,5% 0,25 nhiên nhiên (TN12) Số câu 12 3 3 2 20 Số điểm 3,0 3,0 3,0 1,0 10,0 Tỉ lệ 100 30% 30% 30% 10% %
ĐỀ KIỂM TRA CUỐI HỌC KỲ I – TOÁN 6
I. PHẦN TRẮC NGHIỆM (3 điểm)
Câu 1. Gọi A là tập hợp các số tự nhiên nhỏ hơn 5. Cách viết đúng là: A. A= {1; 2; 3; 4} B. A= {0; 1; 2; 3; 4} C. A= {1; 2; 3; 4; 5}
D. A= {0; 1; 2; 3; 4; 5}
Câu 2. Kết quả của 3 5 là: A. 15. B. 25. C. 5. D. 125.
Câu 3. Không thực hiện phép tính, hãy cho biết trong các tổng sau, tổng chia hết cho 5 là: A. 10 + 25 + 34 + 2000 B. 5 + 10 + 70 + 1995 C. 25 + 15 + 33 + 45
D. 12 + 25 + 2000 + 1997
Câu 4 . Trong các số: 2; 3; 4; 5 số nào là hợp số? A. 2 B. 3 C. 4 D. 5
Câu 5 . Trong các phát biểu sau, phát biểu nào sai? A. 9 N . B. 6 −  N . C. 3 −  Z . D. 0 N .
Câu 6. Hãy chỉ ra đáp án sai trong các đáp án sau. Số âm biểu thị : A. Nhiệt độ dưới B. Số tiền lỗ
C. Độ cao dưới mực nước biển D. Độ viễn thị
Câu 7. Trong các hình sau, hình nào có tất cả các góc không bằng nhau?
A. Hình tam giác đều. B. Hình vuông.
C. Hình thang cân. D. Lục giác đều
Câu 8. Hình nào có hai đường chéo bằng nhau? A. Hình vuông. B. Hình bình hành.
C. Hình tam giác đều. D. Hình thoi
Câu 9. Hình tam giác đều có mấy trục đối xứng? A. 1. B. 2. C. 3. D. 4.
Câu 10. Hình vuông có mấy trục đối xứng? A. 1. B. 2. C. 3. D. 4.
Câu 11. Hình nào sau đây không có tâm đối xứng? A. Hình tam giác đều.. B. Hình chữ nhật.
C. Hình bình hành. D. Hình vuông.
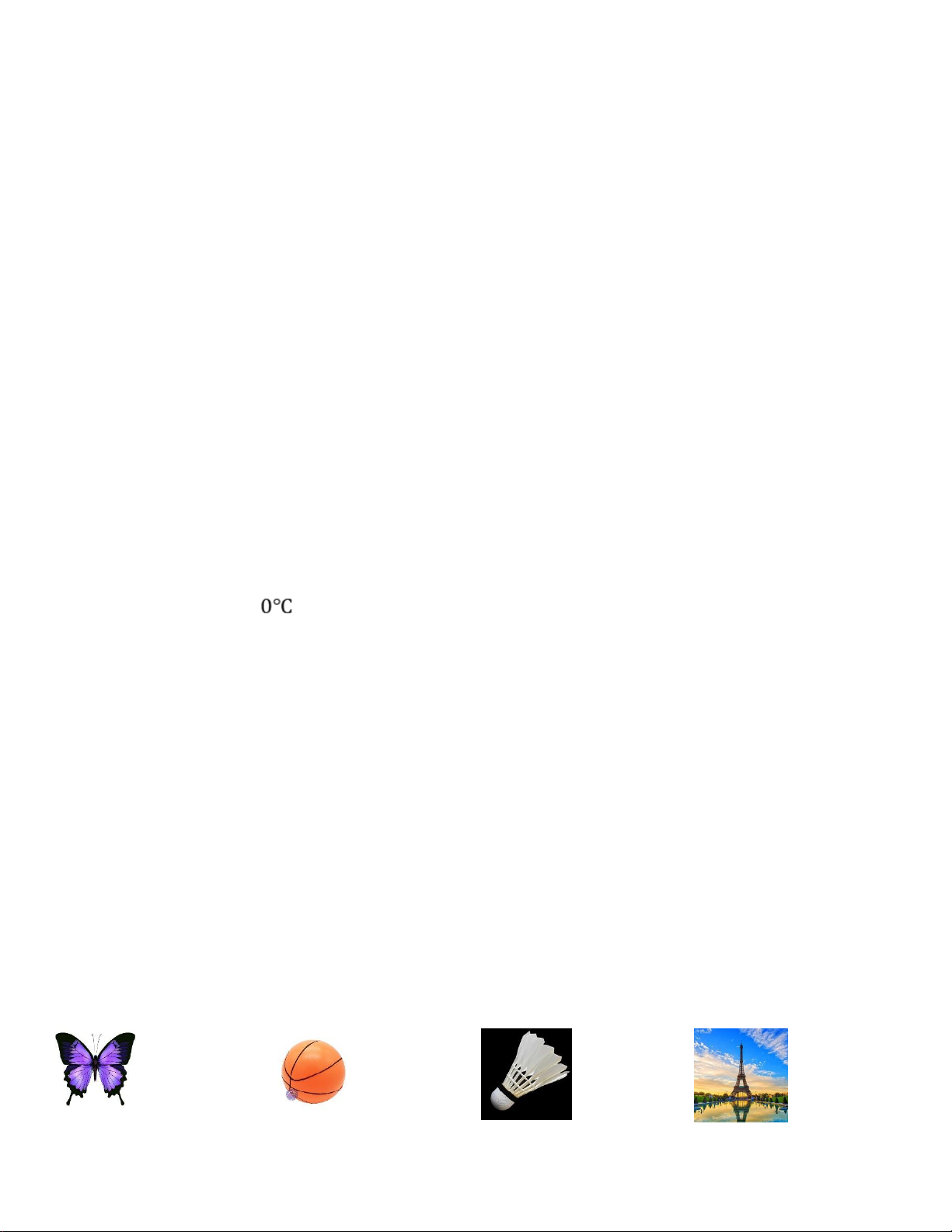
Câu 12. Trong các hình sau, hình nào có tâm đối xứng (1) (2) (3) (4) A.(3) B.(1) C.(2) D.(4)
II. PHẦN TỰ LUẬN(7 điểm)
Câu 13. (2,0 điểm).
Thực hiện các phép tính sau: a) 2 2 8 : 4.3 + 2.3 b) 645 − ( 3 − 8) + ( 4 − 5)
Câu 14 . (3,0 điểm)
1. Tìm số nguyên x, biết: a) 68 – 2( x + 4) = 1
− 2 b) (2x − 3).7 = 35
2. Tìm số tự nhiên x biết: (2x + 7)  (x − 2)
Câu 15. (0,5 điểm)
Hai lớp 6A và 6B nhận trồng một số cây như nhau. Mỗi học sinh lớp 6A phải trồng 6 cây,
mỗi học sinh lớp 6B phải trồng 8 cây. Tính số cây mỗi lớp phải trồng, biết rằng số cây đó trong khoảng từ 170 đến 200.
Câu 16. (1,0 điểm)
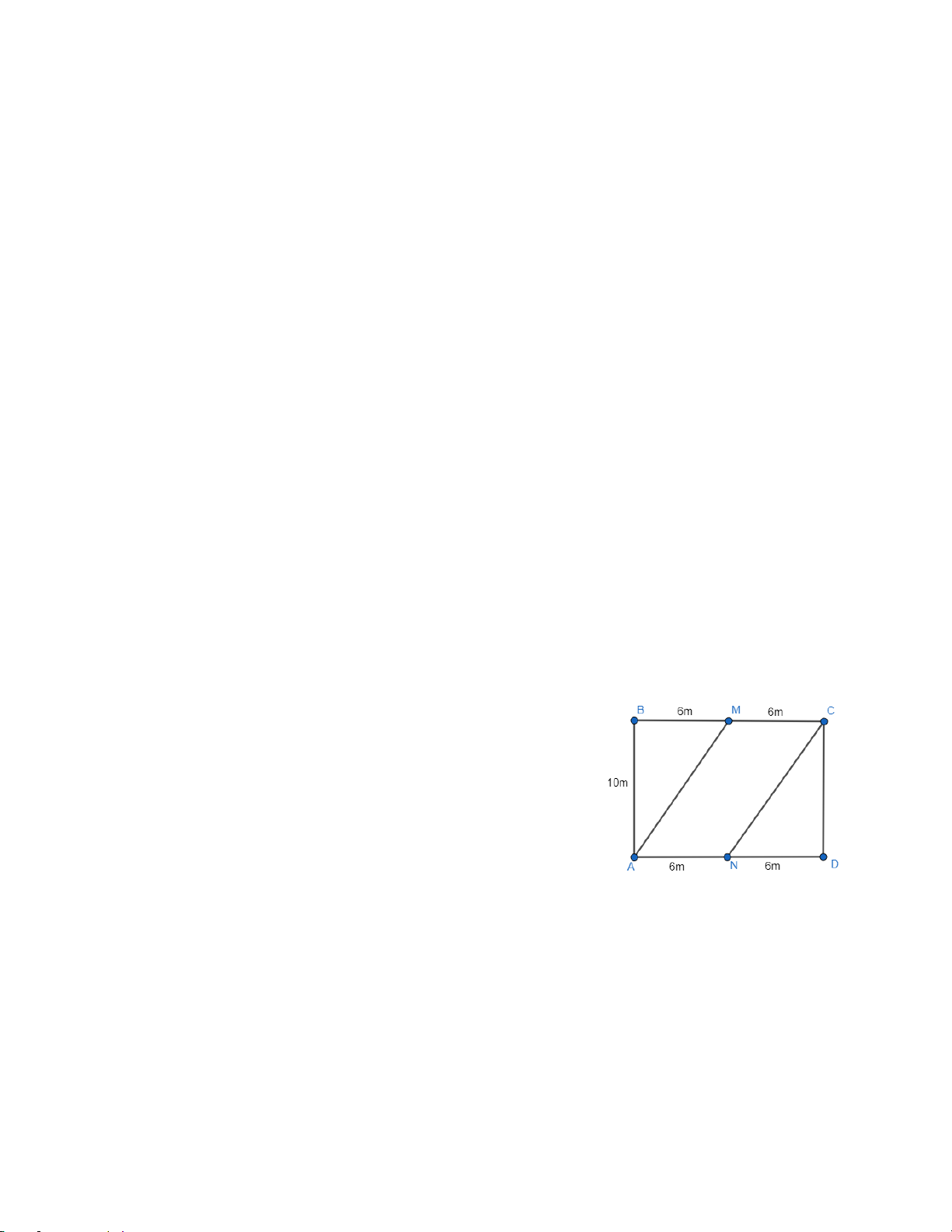
Trên một mảnh đất hình chữ nhật có chiều dài 12m,
chiều rộng 10m, người ta chia khu để trồng hoa, trồng cỏ
như hình bên. Hoa sẽ được trồng ở khu vực hình bình hành
AMCN, cỏ sẽ được trồng ở phần đất còn lại. Tiền công để
trả cho mỗi mét vuông trồng hoa là 50 000 nghìn đồng,
trồng cỏ là 40 000 đồng. Tính số tiền công cần chi trả để trồng hoa và cỏ.
Câu 17. (0,5 điểm)
Everest thuộc dãy Hy Mã Lạp Sơn (Ấn Độ) là ngọn núi cao
nhất của thế giới, có độ cao 8848 mét. Rãnh Mariana ở Thái Bình
Dương, nơi được coi là sâu nhất dưới biển, có độ sâu 11034m.
Hãy tính sự chênh lệch ở hai địa điểm này là bao nhiêu mét (với
qui ước mực nước biển ở vạch số 0).
ĐÁP ÁN VÀ THANG ĐIỂM
I. PHẦN 1: CÂU HỎI TRẮC NGHIỆM KHÁCH QUAN Câu 1 2 3 4 5 6 7 8 9 10 11 12 hỏi Đáp B D B C B D C A C D A C án
II. PHẦN 2: CÂU HỎI TỰ LUẬN Câu Nội dung Điểm 13 a) 82:4.3 + 2.32 0,25 = 64:4.3 + 2. 9 (2,0 = 16.3 + 18 0,25 điểm) = 48 + 18 0,5 = 66 0,5 b) 645 − ( 3 − 8) + ( 4
− 5) = 645+ 38− 45 = 645− 45+ 38 = 0,5
645 − 45 + 38 = 600 + 38 = 638 68 – 2 x + 4 = 1 − 2 14 a) ( ) 2(x + 4) = 80 (2,5 0,5 x + 4 = 40 điểm) x = 36 0,5 Vậy x = 36 b) (2x − 3).7 = 35 2x  − 3 = 5 0,5  x 2 = 8 x 3
 2 = 2  x = 3 0,5 c) (2x + 7)  (x − 2) 0,25
Ta cã 2(x − 2)  (x − 2)  (2x + 7) − 2(x − 2)  (x − 2)
Hay 11  (x − 2)  x − 2 Ư(11)  x − 2 = 1 hoặc x − 2 = 11
hoặc x − 2 = -1, hoặc x − 2 = -11 0,25
Do đó x = 3; x = 13; x= 1; x= - 9
Gọi số cây mỗi lớp 6 phải trồng là x (cây) ( * x  N ) 15 . 0,25
Mỗi học sinh lớp 6A phải trồng 6 cây, mỗi học sinh lớp 6B phải trồng
8 cây và số cây trong khoảng từ 170 đến 200 nên:
x 6, x 8 và170  x  200 0,25
 x BC(6,8) và 170  x  200 Ta có: 3 6 = 2.3; 8 = 2 3
 BCNN(6,8) = 2 .3 = 24
 BC(6,8) = B(24) = 0;24;48;72;96;120;144;168;192;216;.. . 0,25
Do 170  x  200 suy ra x = 192. Vậy số cây mỗi lớp 6 phải trồng là 0,25 192 cây. 16
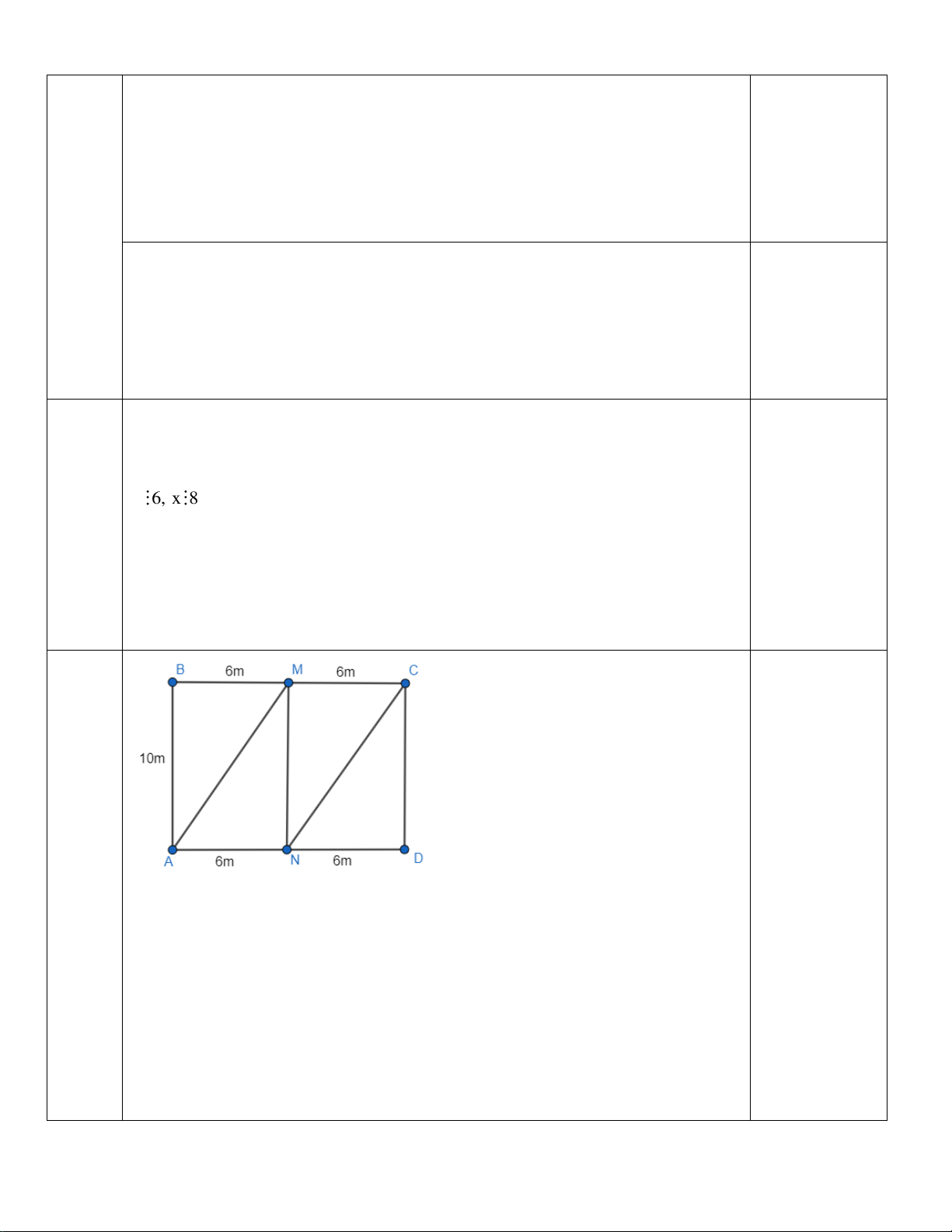
Dễ thấy trong hình bình hành AMCN chiều cao tương ứng của cạnh AN là MN và MN = AB = 10m
Do đó diện tích hình bình hành AMCN là: 6. 10 = 60 (m2) 0,25
Diện tích hình chữ nhật ABCD là: 10. 12 = 120 (m2)
Phần diện tích còn lại trồng cỏ là: 0,25 120 - 60 = 60 (m2)
Số tiền công cần để chi trả trồng hoa là:
50 000. 60 = 3 000 000 (đồng)
Số tiền công cần để chi trả trồng cỏ là:
40 000. 60 = 2 400 000 (đồng) 0,25
Số tiền công cần để chi trả trồng hoa và cỏ là:
3 000 000 + 2 400 000 = 5 400 000 (đồng) 0,25
Vậy số tiền công cần để chi trả trồng hoa và cỏ là 5 400 000 đồng. 17
So với mực nước biển thì độ cao của đỉnh Everest là 8848m 0,25
Độ sâu của rãnh Mariana là -11034m
Khoảng cách cần tìm là : 8848-(-11034)= 19882(m) 0,25