Đề thi học kỳ 1 Toán 10 năm học 2018 – 2019 trường Yên Mô B – Ninh Bình

SỞ GD&ĐT NINH BÌNH
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT YÊN MÔ B
Môn : TOÁN - LỚP 10
Năm học 2018 – 2019
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Họ và tên thí sinh:………………………………………….….
Số báo danh: …………………………. MÃ ĐỀ 101
I. PHẦN TRẮC NGHIỆM (5,0 điểm) 2x  4
Câu 1. Tập xác định của hàm số y  là: x 1 A. D  R .
B. D  R \   1 .
C. D  R \   2 .
D. D  R \ 1;  2 .
Câu 2. Điều kiện xác định của phương trình x 1  3 là: A. x  8 . B. x  1  . C. x  1  . D. x  1  .
Câu 3. Cho hai tập hợp A  2; 
5 , B  0;6 . Tìm A  B .
A. A  B  0;5 .
B. A  B  0;5 .
C. A  B  0;5 .
D. A  B  2;6 .
Câu 4. Mệnh đề phủ định của mệnh đề 2 P : " x
  R, x 1  0" là A. 2 P : " x
  R, x 1  0". B. 2 P : " x
  R, x 1  0" . C. 2 P : " x
  R, x 1  0" . D. 2 P : " x
  R, x 1  0".
Câu 5. Hàm số nào sau đây là hàm số chẵn: A. 4
y  x  3x . B. 4
y  x  2x . C. 3
y  x  2x . D. 4 2
y  x  2x  3 .
Câu 6. Tìm tất cả các giá trị của m để hàm số y  2m  
1 x  m  3 đồng biến trên R . 1 1 A. m  . B. m  . C. m  3 . D. m  3 . 2 2
Câu 7. Biết Parabol  P 2
: y  ax  4x  c có đỉnh I  1
 ; 5 . Tính S  a  c . A. S  1 . B. S  5 . C. S  5 . D. S  1 . Câu 8. Cho hàm số 2
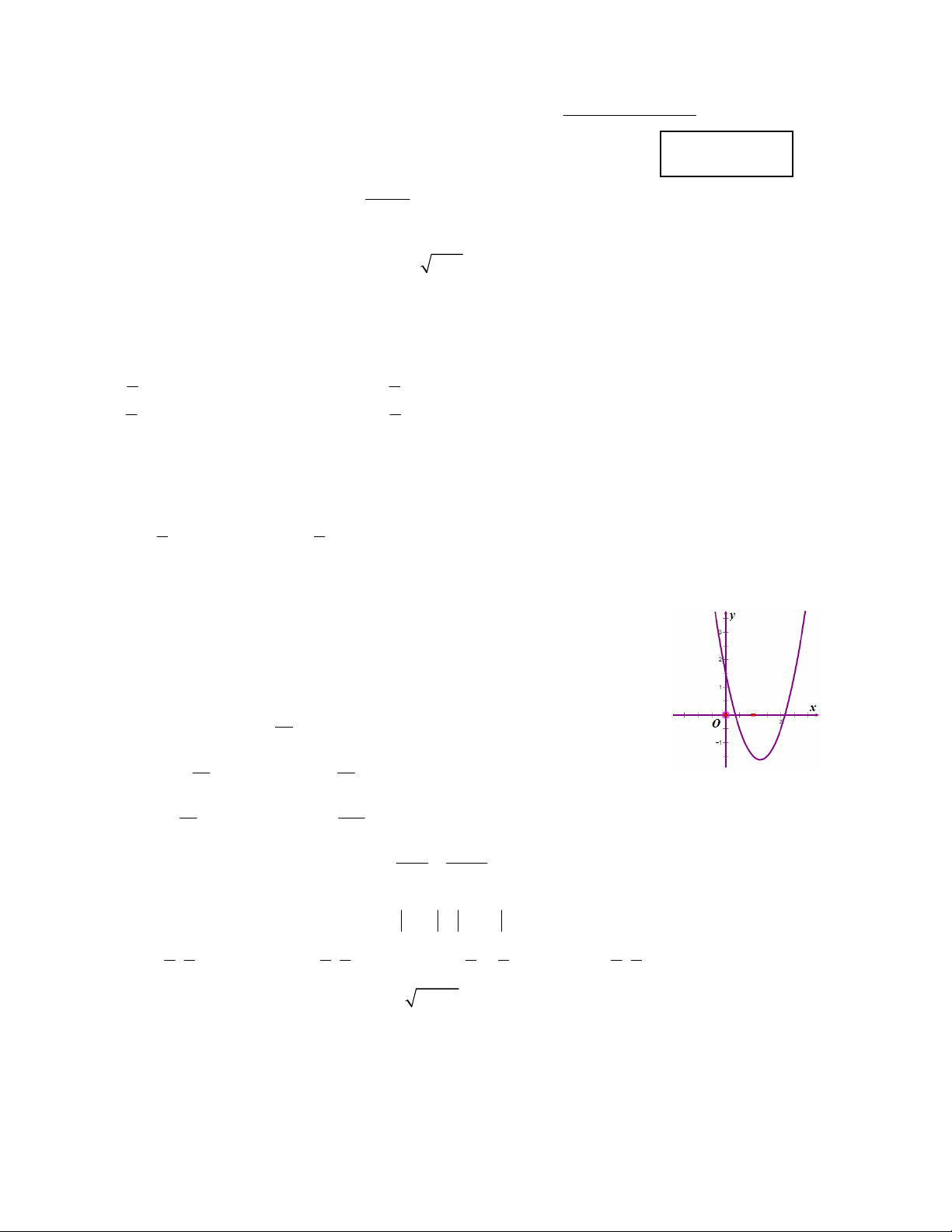
y  ax  bx  c có đồ thị như hình bên. Mệnh đề nào sau đây đúng?
A. a  0,b  0,c  0.
B. a  0,b  0,c  0.
C. a  0,b  0,c  0.
D. a  0,b  0,c  0. 12
Câu 9. Cho biết sin   với 0 0
0    90 . Tính cos ? 13 5 5 A. cos   . B. cos  . 13 13 1 25 C. cos  . D. cos  . 13 169 1 2x 1
Câu 10. Số nghiệm của phương trình x   là x 1 x 1 A. 0 . B. 3 . C. 2 . D. 1.
Câu 11. Tập nghiệm S của phương trình x  2  3x  5 là:  3 7   3 7   7 3   7 3  A. S   ; . B. S   ; .
C. S   ;  . D. S   ; .  2 4   2 4   4 2   4 2 
Câu 12. Tập nghiệm S của phương trình 2x  3  x  3 là A. S   . B. S    2 . C. S    6 . D. S  6;  2 .
x  2 y  3z  0  Câu 13. Gọi  ;
x y; z  là nghiệm của hệ 2x  y  2z  1
 . Tính B  10x  2018 y  2019z . 3
 x  y  z  5  A. B  9 B. B  11  C. B  11 D. B  9 Trang 1
Câu 14. Trong hệ trục tọa độ Oxy, cho 2 điểm A0; 3
 , B 4;5 . Tọa độ trung điểm M của đoạn AB là: A. M (2; 4) . B. M (3; 1) . C. M (4; 2) . D. M (2;1) .
Câu 15. Trong hệ trục tọa độ Oxy, cho A  BC biết (
A 1; 2), B(3; 4),C(5;  3) . Tọa độ trọng tâm G của A  BC là: A. G(9;3) . B. G(3;1) . C. G( 2  ;1) . D. G 3;0 .    
Câu 16. Cho hai vectơ u  5;  
1 và v  3; 2 . Số đo góc giữa 2 vectơ u và v là: A. 0 30 . B. 0 45 . C. 0 60 . D. 0 135 . Câu 17. Cho A
 BC biết A1; 2, B 3;   1 ,C 6 
;1 . Mệnh đề nào sau đây đúng? A. A
 BC vuông tại A . B. A
 BC vuông tại B . C. A
 BC vuông tại C . D. A  BC đều.   Câu 18. Cho A
 BC đều có cạnh bằng 4 . Tính B . A BC ?         A. B . A BC  8 . B. B . A BC  16 . C. B . A BC  8  . D. B . A BC  16 .   
Câu 19. Cho hình chữ nhật ABCD biết AB  3; AD  4 . Tính độ dài của u  AB  AD .     A. u  5 . B. u  7 . C. u  12 . D. u  25 .
   Câu 20. Cho A
 BC biết A1; 2, B 3; 2  ,C 2; 3
  . Tìm tọa độ điểm M  Oy sao cho MA  MB  MC nhỏ nhất. A. M 0;2 . B. M 0  ;1 . C. M 0;   1 . D. M 0;2 .        
Câu 21. Cho 2 vectơ a, b thỏa mãn: a  6, b  5, a  b  7 . Tính . a b ?         A. . a b  6 . B. . a b  6 . C. . a b  12  . D. . a b  12 .
Câu 22. Cho A
 BC biết AC  2 AB ; AD là đường phân giác trong góc ,
A  D  BC  . Biết rằng    AD  .
m AB  k.AC . Giá trị của biểu thức S  3m  2019k bằng A. 1350 . B. 1347 . C. 677 . D. 675 .
Câu 23. Có bao nhiêu giá trị m nguyên để phương trình 4 2
x  4x  m  3  0 có 4 nghiệm phân biệt. A. 3 . B. 4 . C. 5 . D. vô số.
Câu 24. Biết phương trình  x   x   2 1
3  3 x  4x  5  2  0 có 2 nghiệm phân biệt x , x . Giá trị của 1 2
biểu thức T  x  x  5x x là 1 2 1 2 A. T  17  . B. T  23. C. T  51  . D. T  59  .
Câu 25. Có tất cả bao nhiêu giá trị m nguyên thuộc 10;10 sao cho phương trình 2 3
x  mx  4  4 x  4x có nghiệm. A. 11. B. 15 . C. 14 D. 10 .
II. PHẦN TỰ LUẬN (5,0 điểm)
Câu 1 (2,0 điểm). Cho hàm số 2
y  x  2x  3 có đồ thị  P .
a) Khảo sát sự biến thiên và vẽ đồ thị hàm số trên.
b) Tìm m để đường thẳng d : y  6x  m cắt  P tại 2 điểm phân biệt có hoành độ x , x sao cho 1 2 2 2
x  x  3 x  x  2  0 . 1 2  1 2 
Câu 2 (2,0 điểm). Cho A
 BC biết A1; 2, B 5;5,C 4;6 .   a) Tính A .
B AC . Chứng minh rằng A  BC cân.
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành.
c) Tìm tọa độ điểm M  Ox sao cho ABM vuông tại A .
Câu 3 (1,0 điểm): Giải hệ phương trình và phương trình sau: x  y  3 a)  .
b)  x   x    x   2 1 3 7
x 10  x  6x 1 . 2 2
x  y  2x  2 y  11 
................Hết............... Trang 2
SỞ GD&ĐT NINH BÌNH
HƯỚNG DẪN CHẤM ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THPT YÊN MÔ B
Môn : TOÁN - LỚP 10
Năm học 2018 – 2019
I. PHẦN TRẮC NGHIỆM (25 câu, mỗi câu 0,2 điểm) MÃ 101 Câu 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Đáp B B A A D B D C B D A C A D B B B A A C B D A C A án MÃ 102 Câu 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Đáp D B B B A A A B B A C A D D D D A D A C C A A D A án MÃ 103 Câu 1 2 3 4 5 6 7
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Đáp A A B B B D D D B D A C A D B B A A C B B C A D B án MÃ 104 Câu 1 2 3 4 5 6
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Đáp D B B A A A A B B D C A D D D D A A B B C A C D B án
II. PHẦN TỰ LUẬN (5,0 điểm) Câu Đáp án Điểm
 Tập xác định: D  R . b Ta có:   1  . với x  1   y  4  2a 0.25
Toạ độ đỉnh: I  1  ;4.
 Trục đối xứng là đường thẳng x  1. + BBT: x   1       y 0.25 1a (1,0 điểm) 4 
 Hàm số đồng biến trên  1  ; 
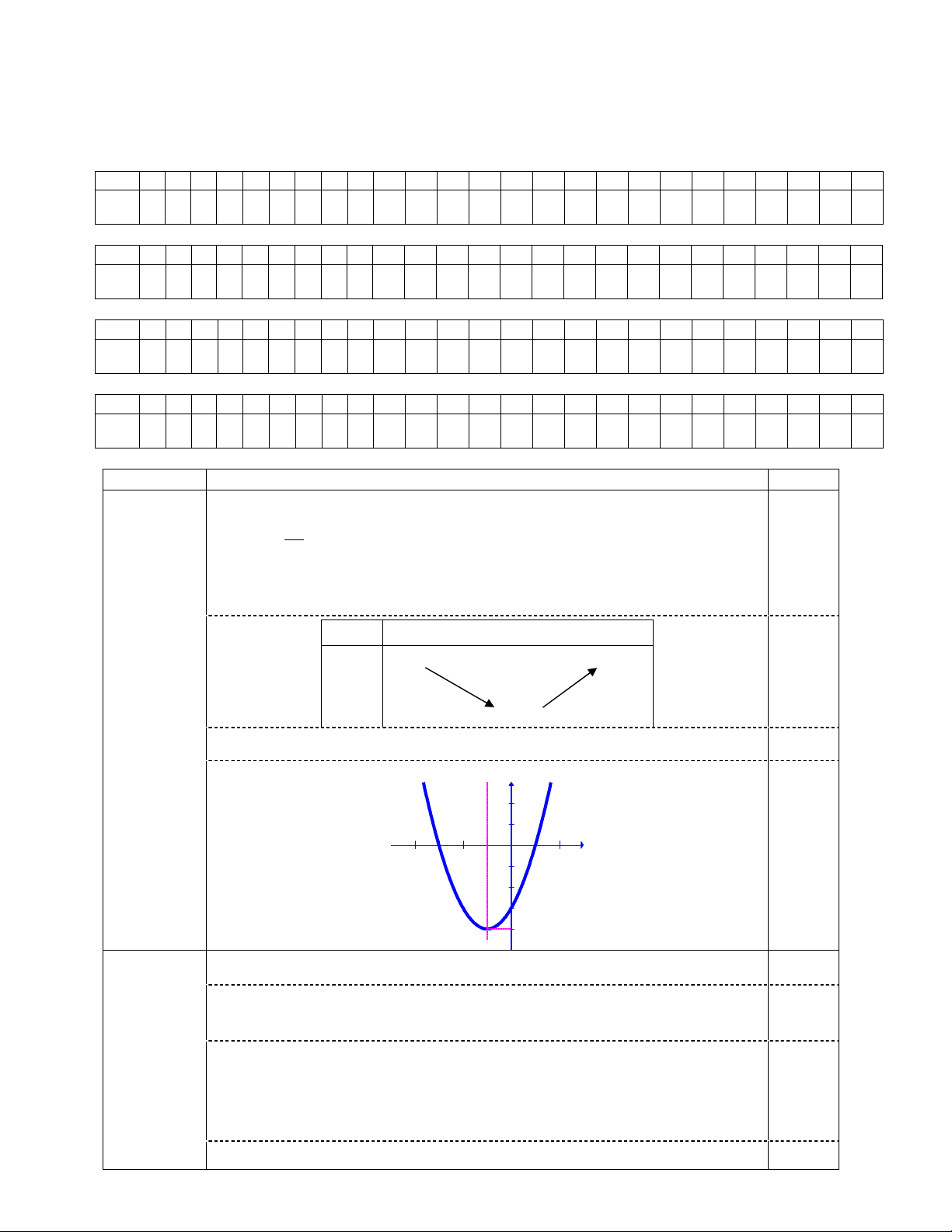
 , nghịch biến trên  ;    1 . 0.25  Đồ thị: y 2 1 x -4 -3 -2 -1 0 1 2 0.25 -1 -2 -3 -4 + Xét PT: 2 2
x  2x  3  6x  m  x  4x  3  m  0   1 0.25
+ d cắt (P) tại 2 điểm phân biệt  PT(1) có 2 nghiệm phân biệt x , x 1 2 0.25  '  0  4  ( 3
  m)  0  m  7.  1b x   x  4  (1,0 điểm) + Ta có 1 2  . x  x  3   m  1 2  0.25
x  x  3x  x   2  0  x  x 2 2 2
 2x x  3 x  x  2  0 1 2 1 2 1 2 1 2  1 2  2  4  2( 3
  m)  3.4  2  0  m  6  (t/m). 0.25 Trang 3  
Ta có: AB  4;3,AC  3; 4. 0.25   2a
AB.AC  4.3  3.4  24 . 0.25 (1,0 điểm) +Ta có: 2 2
AB  4  3  5; AC  5 . 0.25  ABC  cân tại A . 0.25  
Gọi D x ;y  AD  x  1;y  BC   D D 2;  1; 1 D D    0.25 2b
Tứ giác ABCD là hình bình hành  AD  BC (0,5 điểm) x  1  1 x   0  D  D     . Vậy D 0;3 . y   2  1 y   3 0.25  D   D   
Gọi M x; 
0  Ox . Ta có: AB  4; 
3 ; AM  x 1;  2   0.25 2c AB 
M vuông tại A  AB.AM  0 (0,5 điểm) 5 5   4x  
1  3.2  0  x    . Vậy M  ; 0 . 0.25 2 2  x   y  3   1  . 2 2 x 
 y  2x  2y  11  2  +  
1  y  3  x . Thế vào 2 ta có: 3a 0.25 (0,5 điểm) x   1
x    x2 2 3
 2x  23  x  11 2 2x 6x 4 0       . x   2 
+ Với x  1  y  2;x  2  y  1. Vậy hệ có nghiệm: 1;  2 , 2;  1 . 0.25 x   3  0  +Điều kiện   x  3 . x   10  0 
x   x  x   2 1 3 7
x  10  x  6x  1
 x   x    x   x    2 1 3 3 7 10
4  x  x  30 x  6 x    x    x   6 1 7 
 x  5x   6 0.25 x  3  3 x  10  4      x  x 1 x 7 6  x 5       0  3b  x  3  3 x  10  4   (0,5 điểm) x  6    x  1 x  7     x   5  0   *   x  3  3 x  10  4  2 x  x  x  x  7 1 1 7  Ta có: VT   *       3   3 x 3 3 x 10 3           x   1 1       x   1 2 1 . 7 .   . 0.25   
  0, x  3    3    3 x 3 3 x 10 3   Phương trình   * vô nghiệm.
Vậy phương trình đã cho có nghiệm duy nhất x  6 .
................Hết.............. Trang 4