



Preview text:
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 12
ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2019-2020 Môn: Toán học 7 Thời gian: 90 phút
(Không kể thời gian phát đề)
Câu 1 (2 điểm): Tính giá trị của các biểu thức 5 7 5 16 2 19 6 6 6 a) 5 0,5 b) . . 25 27 23 27 23 11 5 11 5 2 5 0 1 c) 2 . ( 2 0 1 8) 6 4 4
Câu 2 (2,5 điểm): Tìm x, biết: 2 3 1 2 1 3 49 a) 2x b) x : 2 4 7 2 4 64 3 1 c) x 2x 1 2 0 d) 4 2 8 4
Câu 3 (1,5 điểm): Trong một hội thi thiết kế tập san, vẽ tranh tuyên truyền
phòng chống HIV/AIDS, ban tổ chức nhận được 250 bức tranh của bốn khối 6; 7;
8; 9. Biết rằng số bức tranh của các khối 6, 7, 8, 9 lần lượt tỉ lệ với 2; 5; 8; 10. Hỏi
khối 7; 8 đã gửi về ban tổ chức bao nhiêu bức tranh? 1
Câu 4 (0,5 điểm): Một máy photocopy siêu tốc in được 1 bản trong giây. 3
Hỏi với tốc độ như vậy, để in được 3060 đề kiểm tra thì máy phải in trong thời gian bao nhiêu phút?
Câu 5 (0,5 điểm): Bạn Hòa đặt xe Grab đi từ nhà đến trường với vận tốc
50km/h hết 15 phút. Hỏi lúc về Hòa đi xe đạp điện với bạn Bình cũng theo con
đường ấy với vận tốc 25km/h thì hết bao nhiêu phút?
Câu 6 (3 điểm): Cho ΔABC có ba góc nhọn (AB < AC). Gọi M là trung điểm
của BC. Vẽ tia AM, trên tia AM lấy điểm D sao cho MA = MD. a) Chứng minh ΔAMB = ΔDMC
b) Vẽ AH BC tại H; DK BC tại K. Chứng minh AH = DK
c) Gọi E là trung điểm của AH, F là trung điểm của DK. Chứng minh E, M, F thẳng hàng. Hết
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 12
ĐÁP ÁN ĐỀ KIỂM TRA HỌC KỲ I NĂM HỌC 2019 -2020 Môn: Toán 7 Câu Nội dung Điểm 5 7 5 16 5 0,5 27 23 27 23 5 5 7 16 0,25 5 0,5 a) 27 27 23 23 Câu1 5 1 0,5 (2 điểm) 6,5 0,25 2 b) 19 6 6 6 . . 25 11 5 11 5 19 6 36 6 . . 5 11 5 11 5 0,25 6 19 36 ( ) 5 5 11 11 6 55 . 5 5 11 0,25 6 5 1 0,25 c) 25 0 1 2. (2018) 64 4 0,25 đ 5 1 2 . 1 8 4 0,25 đ 5 1 1 4 4 1 1 0,25 đ 2 2 3 1 Câu 2 a) 2x 2 4 (2,5 điểm) 9 1 2x 4 4 0,25 9 1 2x 4 4 2x 2 x 1 0,25 2 1 3 4 9 b) x : 7 2 4 6 4 2 1 3 8 x . 0,25đ 7 2 4 7 2 1 6 x 7 2 7 2 6 1 x 7 7 2 2 19 x 19 x 7 14 4 0,25đ 3 1 x 0 c) 4 2 3 1 x 4 2 3 1 3 1 x x 4 2 hay 4 2 0,25 đ 1 3 1 3 x x 2 4 2 4 0,25 đ 1 5 x x 4 4 0,25 đ x 1 2 2 d) 8 4 x ( 2).( 8) 1 2 4 0,25 x 1 2 4 x 1 2 2 2 0,25 x 1 2 x 1 0,25
- Gọi x, y, z, t theo thứ tự là số bức tranh của các khối 0,25đ 6,7,8,9 Câu 3 - Lập được: x y z t = = và x + y + z + t= 250 0,25 đ (1,5 điểm) 2 5 8 10
- Áp dụng tính chất dãy tỉ số bằng nhau. x y z t x y z t 250 0,25 đ Ta có: = = 10 2 5 8 10 25810 25
- Tính được: y = 50; z = 80 0,5 đ
- Trả lời: Vậy: Khối 7 có 50 bức tranh Khối 8 có 80 bức tranh 0,25 đ Câu 4
Thời gian máy photocopy in 3060 đề kiểm tra là:
(0,5 điểm) 3060 . 1/3 = 1020 (giây) 0,25đ Đổi 3060 giây = 17 phút
Vậy Thời gian máy photocopy in 3060 đề kiểm tra học kỳ môn toán là 17 phút 0, 5đ Câu 5 Đổi 15 phút = 1 giờ (0,5 điểm) 4
Quãng đường từ nhà đến trường là: 50. 1 = 12,5 km 0,25đ 4
Thời gian đi từ trường về nhà là: 12,5 =0,5giờ= 30 phút 25 0,25đ
(HS Có thể dùng đại lượng tỉ lệ nghịch để giải)
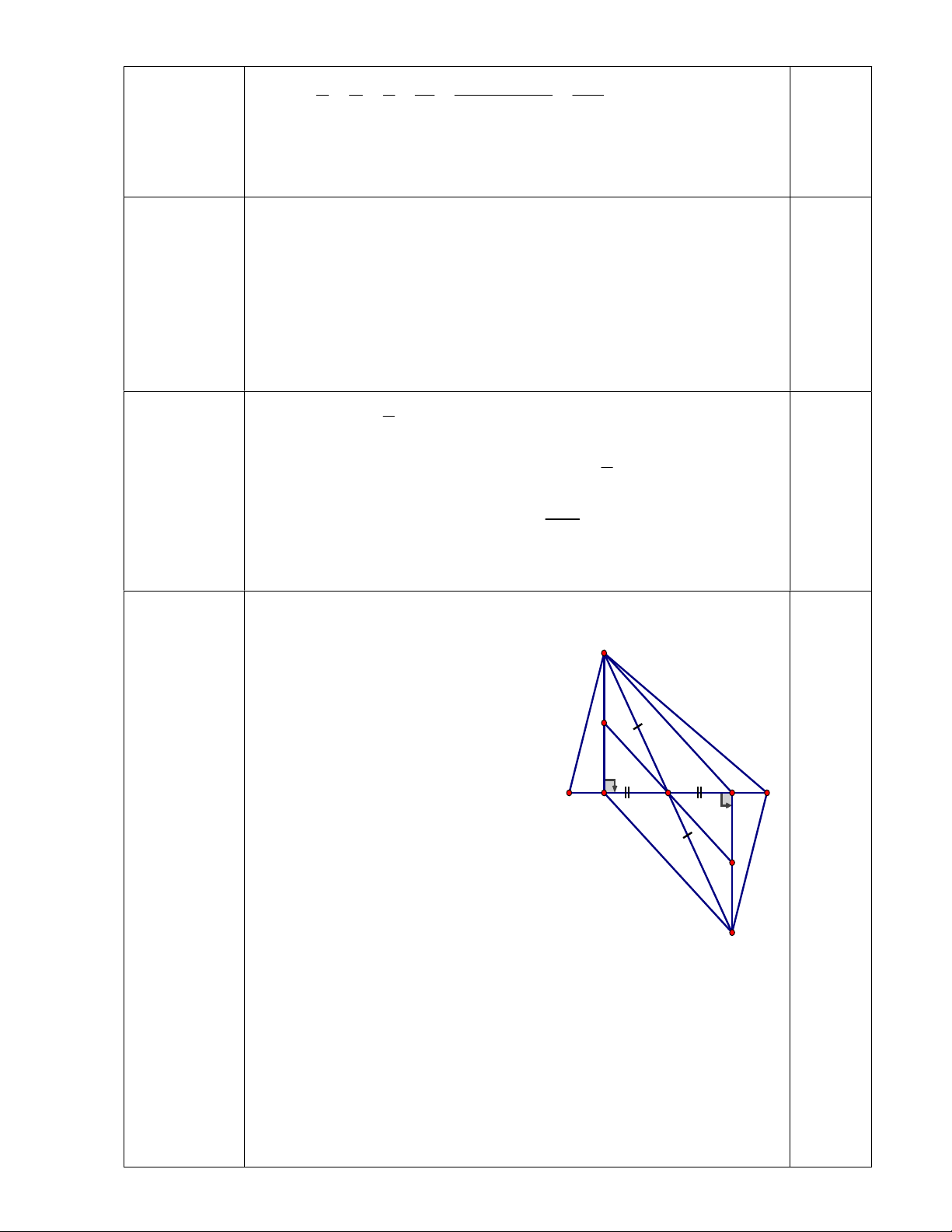
a) Xét Δ AMB và Δ DMC có : A MA = MD (gt) 0,25đ Câu 6 Góc AMB = góc DMC (2 góc 0,25đ (3 điểm) đối đỉnh) MB = MC (gt) E 0,25đ Do đó Δ AMB = Δ DMC 0,25đ (c.g.c) C b) xét ΔAMH vuông và B H M K ΔDMK vuông có : AM = DM (gt) F 0,25đ Góc AMB = góc DMC (2 góc 0,25đ đối đỉnh) Do đó ΔAMH = ΔDMK (ch- 0,25đ gn) D
Cho ta AH = DK (2 cạnh tương ứng) 0,25đ
c) Vì AH = DK (chứng minh trên)
Mà E là trung điểm của AH (gt)
và F là trung điểm của DK (gt) Nên EA = EH = EK = ED 0,25đ Δ EHM = Δ FKM (c.g.c)
Cho ta góc EMH = góc FMK (2 góc tương ứng) 0,25đ
Mà góc EMH + góc EMC = 1800 (do B,M,C thẳng hàng)
Nên góc FMK + góc EMC = 1800 0,25đ
Hay góc FME = 1800 là góc bẹt Vậy E, M, F thẳng hàng 0,25đ
Học sinh làm cách khác nếu đúng vẫn được trọn điểm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO QUẬN 12
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I – NĂM HỌC: 2019-2020 MÔN: TOÁN – LỚP 7 Vận dụng Cấp độ Cấp Nhận biết Thông hiểu Cộng Cấp độ thấp độ Chủ đề cao 1. Thực hiện phép tính (Cộng
Hiểu thứ tự thực hiện Vận dụng lũy thừa, trừ nhân chia SHT, phép tính căn bậc hai, GTTĐ Lũy thừa, căn bậc hai) Số câu 1 2 3 Số điểm; Tỉ lệ % 0,5 5% 1,5 15% 2; 20%
Vận dụng giá trị tuyệt Biết cách tìm x qua 2. Tìm x đối và lũy thừa, căn cách chuyển vế bậc hai, tỉ lệ thức Số câu 1 3 4 Số điểm 0,5 5% 2 20% 2,5;25% Vận dụng tính chất 3. Toán thực tế dãy tỉ số bằng nhau Lập tỉ lệ thức,
Thiết lập theo các dữ thực hiện phép tính Làm toán giảm giá kiện của bài toán trong giải quyết bài liên quan đến %) toán thực tế Số câu 1 1 2 10% Số điểm 1 1,5 15% 2,5; 25%
Vận dụng đại lượng tỉ 4. Đại lượng tỉ lệ lệ nghịch, thực hiện Bài toán chuyển động nghịch phép tính trong giải
quyết bài toán thực tế Số câu 1 1 Số điểm 0,5 5% 0,5;5% Nhận biết Vận dụng hai tam giác 5. Hai tam giác được trường bằng nhau để chứng bằng nhau hợp bằng nhau minh hai cạnh song c-g-c song Số câu 2 1 3 Số điểm 1,5 15% 1 10% 2,5;25% Tổng số câu 2 3 8 13 Tổng số điểm 1,5 2 6,5 10 Tỉ lệ 15% 20% 65% 100% ----- HẾT -----




