lOMoAR cPSD| 45476132 TRƯỜNG THCS
ĐỀ KIỂM TRA HỌC KỲ II NGHĨA TÂN MÔN TOÁN 7 Năm học 2017-2018 (Thời gian: 90 phút)
I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm)
Ghi lại chữ cái đứng trước câu trả lời đúng
Câu 1: Đơn thức 3x y2 3 đồng dạng với đơn thức nào trong các đơn thức sau? A. 3x y2 2 B. x y2 3 C. 2x y3 2 D. 3 x y2 3
Câu 2: Cho đa thức A x y 2 2x y2 2 3xy 2x y2 2 2x 7. Bậc của đa thức A là: A. 1 B. 2 C. 3 D. 4 Câu 3: Cho ABC có B 700, A
500 . So sánh các cạnh của tam giác ta có thứ tự: A. AB < AC < BC B. BC < AC < AB C. AB < BC < AC D. BC < AB < AC
Câu 4: Bộ ba độ dài nào sau đây có thể là độ dài ba cạnh của một tam giác? A. 2cm, 3cm, 6cm B. 2cm, 3cm, 5cm C. 3cm, 5cm, 6cm D. 1cm, 1cm, 3cm
II. BÀI TẬP TỰ LUẬN (8,0 điểm) Bài 1: (1,0 điểm) Cho đơn thức A 1 x y z3 2 . 4xy z3 2 2 a) Thu gọn A
b) Tính giá trị của đơn thức A khi x 1;y 1;z 1 lOMoAR cPSD| 45476132
Bài 2: (1,5 điểm) Cho các đa thức
M x x( ) 4 2x3 4x2 3x 5 và N x( ) 2x3 4x2 3x 1 a) Tính A x M x N x b) Tính B x M x N x
c) Chứng tỏ rằng đa thức B(x) luôn nhận giá trị dương với mọi giá trị củax.
Bài 3: (1,5 điểm) Tìm nghiệm của các đa thức sau a) P x 2x 5 b) K x( ) 3 x3 2x 3x3 4x 3 c) Q x x 3 2x
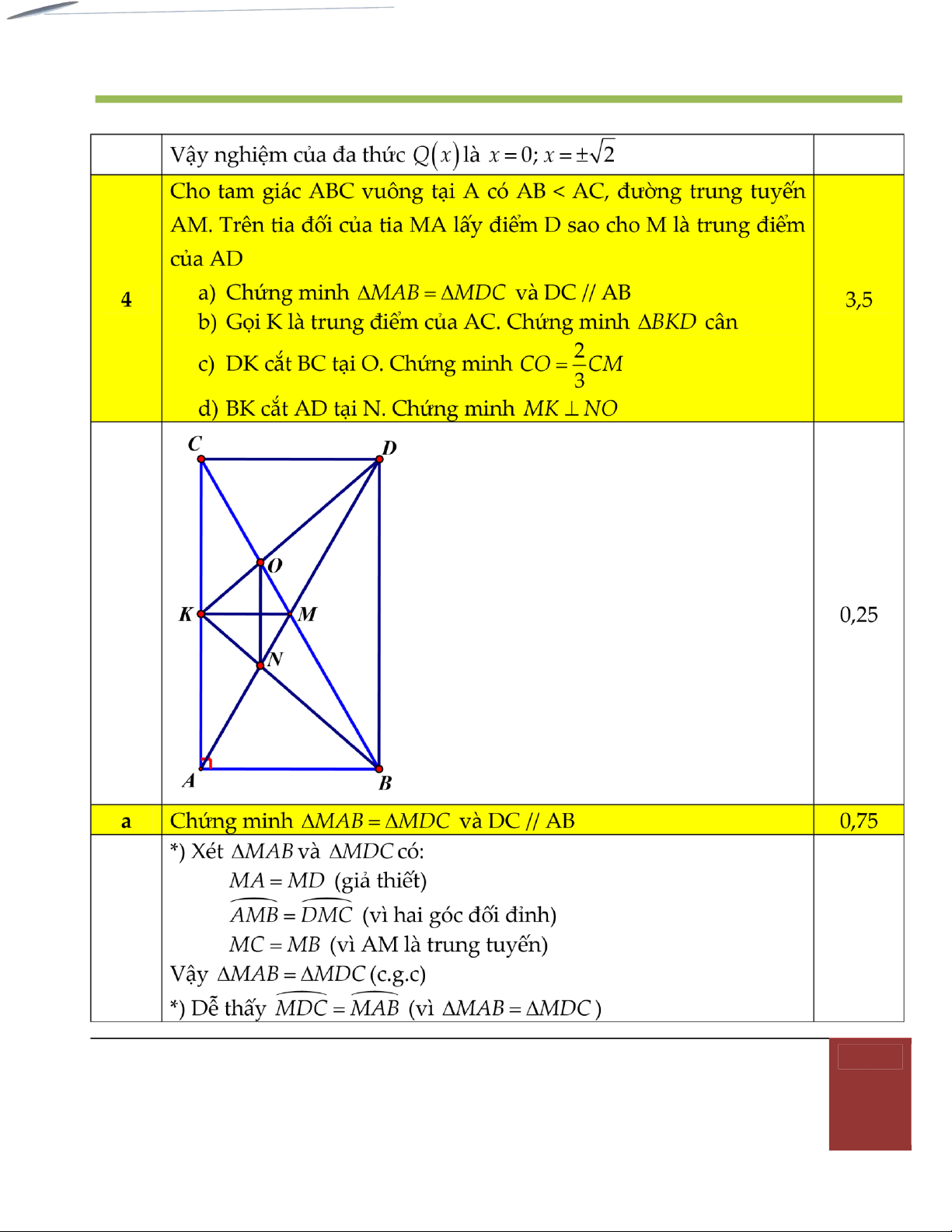
Bài 4: (3,5 điểm) Cho tam giác ABC vuông tại A có AB < AC, đường trung tuyến
AM. Trên tia đối của tia MA lấy điểm D sao cho M là trung điểm của AD a) Chứng minh MAB MDC và DC // AB
b) Gọi K là trung điểm của AC. Chứng minh BKD cân
c) DK cắt BC tại O. Chứng minh CO CM
d) BK cắt AD tại N. Chứng minh MK NO
Bài 5: (0,5 điểm) Tìm giá trị nhỏ nhất của đa thức P x 2 3 x2 2 2 lOMoAR cPSD| 45476132 ĐÁP ÁN THAM KHẢO
I. TRẮC NGHIỆM KHÁCH QUAN (2,0 điểm) Câu 1 Câu 2 Câu 3 Câu 4 B C D C
II. BÀI TẬP TỰ LUẬN (8,0 điểm) Bài Nội dung Điểm Cho đơn thức A 1 x y z3 2 1 1 . 4xy z3 2 2 a Thu gọn A 0,5 A 1 x y z3 2 . 4xy z3 2 1. 4 . x x y y3. . 2. 3 . zz. 2 2x y z4 5 3 2 2 b 0,5
Tính giá trị của đơn thức A khi x 1;y 1;z Thay x 1;y 1;z vào biểu thức Ata có: A 2. 1 . 1 . 45 1 3 2.1.1. 1 1 2 8 4 Cho các đa thức 2 1,5
M x x( ) 4 2x3 4x2 3x 5 và N x( ) 2x3 4x2 3x 1 3 lOMoAR cPSD| 45476132 a 0,5 Tính A x M x N x A x M x N x x4 2x3 4x2 3x5 2x3 4x2 3x 1 A x x42x3 4x2 3x 5 2x3 4x2 3x 1 A x x42x3 2x3 4x2 4x2 3x3x 5 1 A x x44x3 8x2 6x 4 b 0,5 Tính B x M x N x B x M x N x x4 2x3 4x2 3x5 2x3 4x2 3x 1 B x x42x3 4x2 3x 5 B x x42x3 2x3 4x2 4x2 3x3x 5 1 B x x4 6
Chứng tỏ rằng đa thức B(x) luôn nhận giá trị dương với mọi giá c 0,5 trị củax. Ta có x4 0với xnên x4 6 6 0 x Suy ra B x x 4
6 0 với x(điều phải chứng minh) 3
Tìm nghiệm của các đa thức sau 1,5 4 lOMoAR cPSD| 45476132 a 0,5 P x 2x 5 Ta có 2x 5 0 2x 5 x
Vậy nghiệm của đa thức P x là x b 0,5 K x( ) 3 x3 2x 3x3 4x 3 Ta có 3x3 2x 3x3 4x 3 0 3x3 2x x3 3 4x 3 0 2x 3 0 2x 3 x 3
Vậy nghiệm của đa thức K x là x c 0,5 Q x x 3 2x Ta có x3 2x 0 x x 2 2 0 2x 2 00 xx2 02 xx 02 x 5 lOMoAR cPSD| 45476132 6 lOMoAR cPSD| 45476132 7 lOMoAR cPSD| 45476132
Mà hai góc này ở vị trí sole trong của DC và AB do AD cắt Nên DC // AB b
Gọi K là trung điểm của AC. Chứng minh BKD cân 1
*) Ta có DC // AB (chứng minh trên) Mà AB AC (giả thiết)
Nên DC AC(từ vuông góc đến song song) *)Xét DCK và BAK có: CD AB (vì MAB MDC) KCD KAB 90 AK CK (giả thiết) Vậy DCK BAK(c.g.c)
Suy ra KD KB (hai cạnh tương ứng của hai tam giác bằng nhau) Hay BKDcân tại K c 1
DK cắt BC tại O. Chứng minh CO CM 8
Downloaded by Mai Linh Tr?nh (trinhmailinh15@gmail.com) lOMoAR cPSD| 45476132 *)Xét ADCcó:
DK là trung tuyến ứng với cạnh AC (giả thiết)
CM là trung tuyến ứng với cạnh AD (giả thiết) Mà
DK cắt CM tại O (giả thiết)
Nên O là trọng tâm của ADC Suy ra CO CM
(tính chất trọng tâm trong tam giác) d
BK cắt AD tại N. Chứng minh MK NO 0,5
*)Tương tự câu c ta dễ dàng chứng minh được N là trọng tâm của ABC
*)Vì N là trọng tâm của ABC nên MN 1 (tính chất trọng tâm AM 3 trong tam giác) (1) 9 lOMoAR cPSD| 45476132
*) Vì O là trọng tâm của ADC nên MO 1 (tính chất trọng tâm MC 3 trong tam giác) (2)
*) Ta có AM = MC (tính chất đường trung tuyến) (3) MO MN Từ (1); (2); (3) suy ra
1 hay ON / / AC (định lý Talet) MC AM 3 AK AM *) Dễ thấy
1 hay KM / / DC (định lý Talet) AC AD 2
*) Ta có KM / / DC và ON / / AC (chứng minh trên)
Mà DC AC (chứng minh trên)
Nên ON KM (điều phải chứng minh) 5 0,5
Tìm giá trị nhỏ nhất của đa thức P x 2 3 x2 2 10
Downloaded by Mai Linh Tr?nh (trinhmailinh15@gmail.com) lOMoAR cPSD| 45476132 Ta có P x 2 3 x2 2 x x4 2 6 x2 2 2.x2. 1 1 2 1 2 6 2 2 2 2 x 2 1 25 P 2 4 1 2 Dễ thấy x2 0với x 2 Suy ra x2 1 2 25 25 P 25 2 4 4 4
Dấu “=” xảy ra khi và chỉ khỉ x 1 2 0 x 1 2 2 Vậy GTNN của P 25 tại x 1 2 4 11