SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 9 NĂM HỌC 2020 - 2021
Môn thi: Toán lớp 9 THCS ĐỀ THI CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề) Ngày thi: 18/3/2021
(Đề thi gồm 01 trang, 05 câu) Câu 1 (4,0 điểm).  x  y x  y  
x  y  xy  Cho biểu thức 2 : P     : 1    
với x  0; y  0; xy  1. 1 xy 1  xy   1 xy  a) Rút gọn biểu thức . P
b) Tính giá trị của P với y  9  4 5.
Câu 2 (4,0 điểm). Cho phương trình 2
mx  2m  2 x  m  3  0 ( m là tham số).
a) Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm trái dấu.
b) Tìm tất cả các giá trị của tham số m để phương trình có hai nghiệm x , x thỏa 1 2 1 1 mãn:   2. 2 2 x x 1 2 Câu 3 (4,0 điểm). 2 2
xy  x  y  x  2y
a) Giải hệ phương trình 
x 2y  y x 1  2x  2y 
b) Tìm tất cả các số nguyên dương ,
x y, z thỏa mãn phương trình 6 6 4 3 2 2 2 2
x  y 15y  z  75y  3x y z 15x z 125.
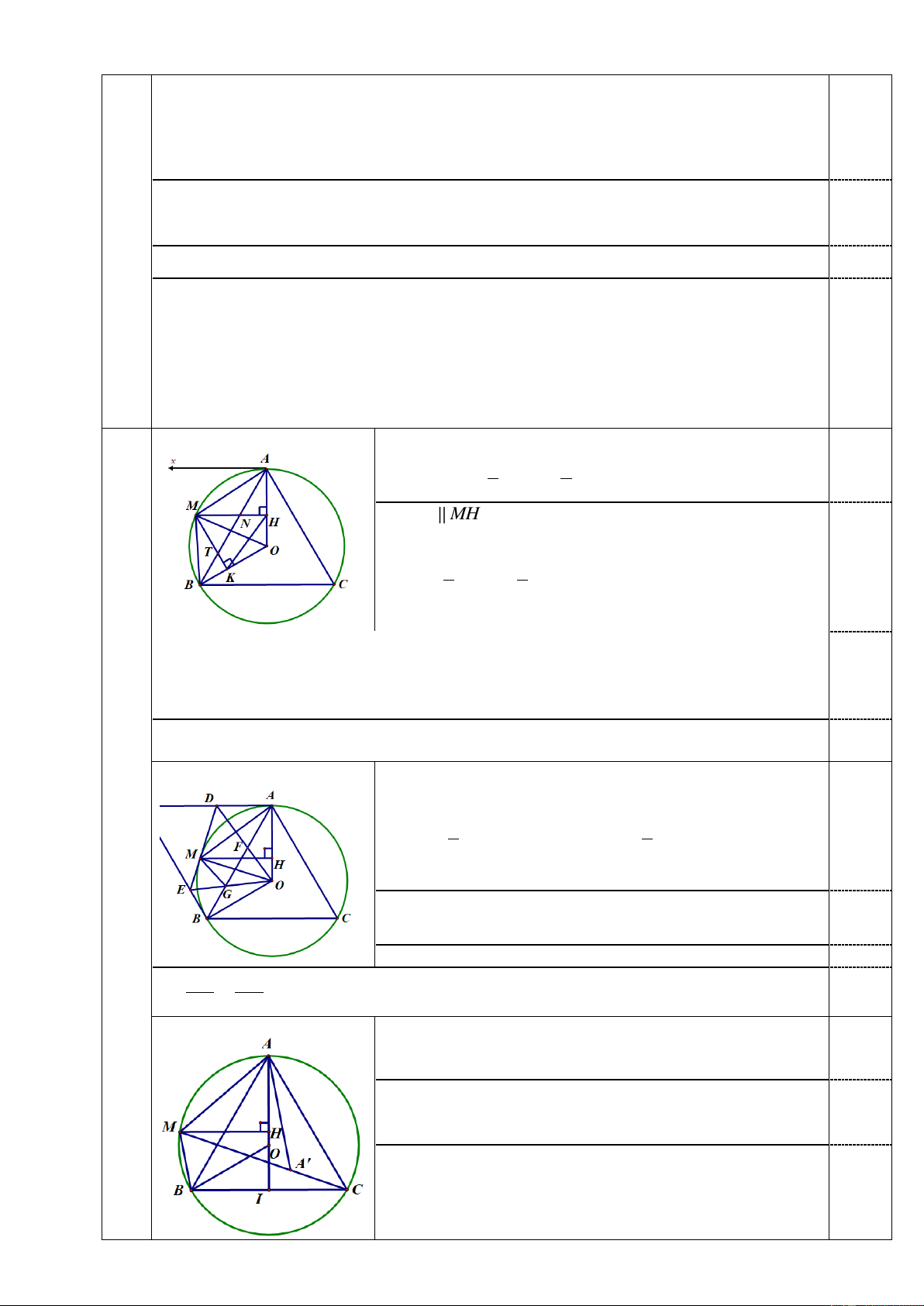
Câu 4 (6,0 điểm). Cho tam giác đều ABC nội tiếp đường tròn  ;
O R. Gọi H là một điểm
di động trên đoạn thẳng OA ( H khác O và HA  HO ). Đường thẳng đi qua H và vuông
góc với OA cắt cung nhỏ AB tại M. Gọi K là hình chiếu vuông góc của M trên . OB
a) Chứng minh BMK  MAB.
b) Các tiếp tuyến của  ;
O R tại A và B cắt tiếp tuyến tại M của  ; O R lần lượt
tại D và E. O ,
D OE cắt AB lần lượt tại F và .
G Chứng minh rằng: O .
E OG  OF.O . D
c) Tìm vị trí điểm H để chu vi tam giác MAB đạt giá trị lớn nhất. Câu 5 (2,0 điểm). 1 1 1 a) Cho a, ,
b c là các số thực dương thoả mãn    6. 2 2 2 a b c 2 2 2 2 2 2 b c c a a b
Tìm giá trị nhỏ nhất của biểu thức Q  a    . 2 2
b  c  b 2 2
c  a  c 2 2 a  b 
b) Cho mỗi điểm trên mặt phẳng được tô bởi một trong hai màu xanh hoặc đỏ.
Chứng minh rằng tồn tại một tam giác mà ba đỉnh và trọng tâm cùng màu.
---------------------Hết---------------------
Họ và tên thí sinh: ………………………....................... Số báo danh: …………...........
Chữ kí giám thị số 1:……………….........Chữ kí giám thị số 2:…..................………....
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 9 NĂM HỌC 2020 - 2021
HƯỚNG DẪN CHẤM THI MÔN TOÁN LỚP 9 THCS
(Hướng dẫn chấm gồm 03 trang)
Chú ý: Những cách giải khác HDC mà đúng thì cho điểm theo thang điểm đã định. Câu Nội dung Điểm
 x  y1 xy x  y1 xy
1 xy  x  y  2xy a) P  : 0,5 1 xy 1 xy x  x y 
y  y x  x  x y  y  y x 1  xy . 0,5 1 xy
1 x  y  xy 2
  y  x y    0,5
1 x1 y 1 (4đ)  2  y 0,5 1 y b) y      2 9 4 5 5 2 0,5 y    2 5 2  5  2 0,5 2   5  2 5 P    1,0 1 9  4 5 5
a) Phương trình có hai nghiệm trái dấu  mm 3  0 1,0  0  m  3. 1,0 b) TH1. m  0 Phương trình  0,5
4x  3  0 (Không thỏa mãn yêu cầu) TH2. m  0
Phương trình có hai nghiệm 2 0,5
x , x   '  0  m  2  mm  3  0  m  4 1 2  2 2  m 2 x  x  2 (4đ) 1 1
x  x  2x x 1 2  1 2  Khi đó  m và 1 2   2   2 0,5 m  3  2 2 x x 1 2 x x 1 2 2 x x  1 2  m  22  m 2  m  3    2  m   m
 2  m 1 (t / m). 0,5 2  m  3     m  2 2
xy  x  y  x  2y (1) a) 
Điều kiện: x  1, y  0 0,5
x 2y  y x 1  2x  2y (2)  Khi đó:  
1   x  y x  2y   1  0 0,5 3
(4đ)  x  2y 1  0  x  2y 1 0,5
Thay vào phương trình (2) ta được:  y   1  2y  2  0  y  2 0,5
y hệ có nghiệm  x; y  5; 2 . b) 6 6 4 3 2 2 2 2
x  y 15y  z  75y  3x y z 15x z 125. 6 3 2 2 2
 x  z 15x z  3x y z  6 4 2
y 15y  75y 125 0,5
 x 3  y 53 2 2 3 2
 z  3x z 2y 5
Áp dụng BĐT Cauchy ta có VT  x 3  y  3 2 2 3 2
 z  x z 2 5 3 y  5 0,5 Dấu "  " xảy ra khi 2 2
x  z  y  5 Phương trình 2 2
 x  y  5  x  yx  y  5 0,5
x  y  5 x  3    (l)
x  y  1 y  2    x  y  1
x  3  z  9  0,5   
x  y  5 y  2
Nghiệm của phương trình là  ; x ;
y z  3;2;9. a)
Qua A kẻ tia tiếp tuyến Ax của (O). 1 1 0,5 Ta có MAx  MOA  sđ AM (1) 2 2
Có Ax MH (cùng vuông góc với OA )
 MAx  AMH (2) 1 1 0,5 MBA  MOA  sđ AM (3) 2 2
Từ (1),(2),(3)  MBA  AMH (5)
OAB cân tại O và 0 0
AOB  120 , BAO  ABO  30
Gọi N,T lần lượt là giao điểm của MH, MK với AB 0,5 Ta có 0
MTB  TBK  TKB  120 , 0
MNA  NAH  NHA  120  MTB  MNA (6)
Từ (5),(6)  MNA đồng dạng BTM  MAN  BMT  BMK  MAB. 0,5 b) Có: 0
DAO  DMO  90 (Tính chất tiếp tuyến)
 tứ giác AOMD nội tiếp (7) 4 1 1 0,5 (6đ) GAM  sđ MOG  GOB  sđ BM ; BM 2 2
 GAM  MOG  tứ giác AMGO nội tiếp (8)
Từ (7), (8) ta có 5 điểm , A , D M , ,
G O cùng nằm trên một 0,5
đường tròn  AGO  ADO  ODM  OGF  đồng dạng ODE  0,5 OE OD   hay O .
E OG  OF.O . D 0,5 OF OG c)
Trên đoạn MC lấy điểm A' sao cho MA'  MA   0,5
AMA' đều  MAB  A AC  0 '  60  BAA'  M  AB  A
 ' AC  MB  A'C  MA  MB  MC Chu vi AMA' là 0,5
MA  MB  AB  MC  AB  2R  AB
Giá trị lớn nhất của chu vi MAB là 2R  AB
Giá trị lớn nhất của chu vi MAB đạt được khi MC là đường kính của 0,5
(O). Khi đó M là điểm chính giữa cung AB
Gọi I là giao điểm của AO và BC  H là trung điểm đoạn AI 3 3 0,5 Ta có AI  R  AH  R 2 4 1 1 1 a) Q     1 1   1 1   1 1  a  b  c        2 2 2 2 2 2  c b   a c   b a  Đặt 1 1 1
 x,  y,  z thì ,
x y, z  0 và 2 2 2
x  y  z  6 a b c 2 2 2  x  y  z  x  y  z Q 2 2 2 2 2 2 y  z z  x x  y x  2  x  y 2 6
6  y  z 6  z2
Áp dụng BĐT Cauchy cho ba số dương ta được 3 x 
 x   x   x  6  x  1
 2x 6  x 6  x  2 2 2 2 1 2 6 6 2 2 2 2 2     32 0,5 2 2  3    x x 6  x  2 2 2  4 2    x x 6  x  2 2 8 2 2 Tương tự y 2 z 2   y  z y 6  y  2 , 8 z 6  z  2 2 2 8 Do đó 2 Q   3 2 2 2 2
x  y  z   8 4 0,5 Đẳng thức xảy ra khi 1
x  y  z 
2 hay a  b  c  2 5 3 2
(2đ) y giá trị nhỏ nhất của Q là . 4 b)
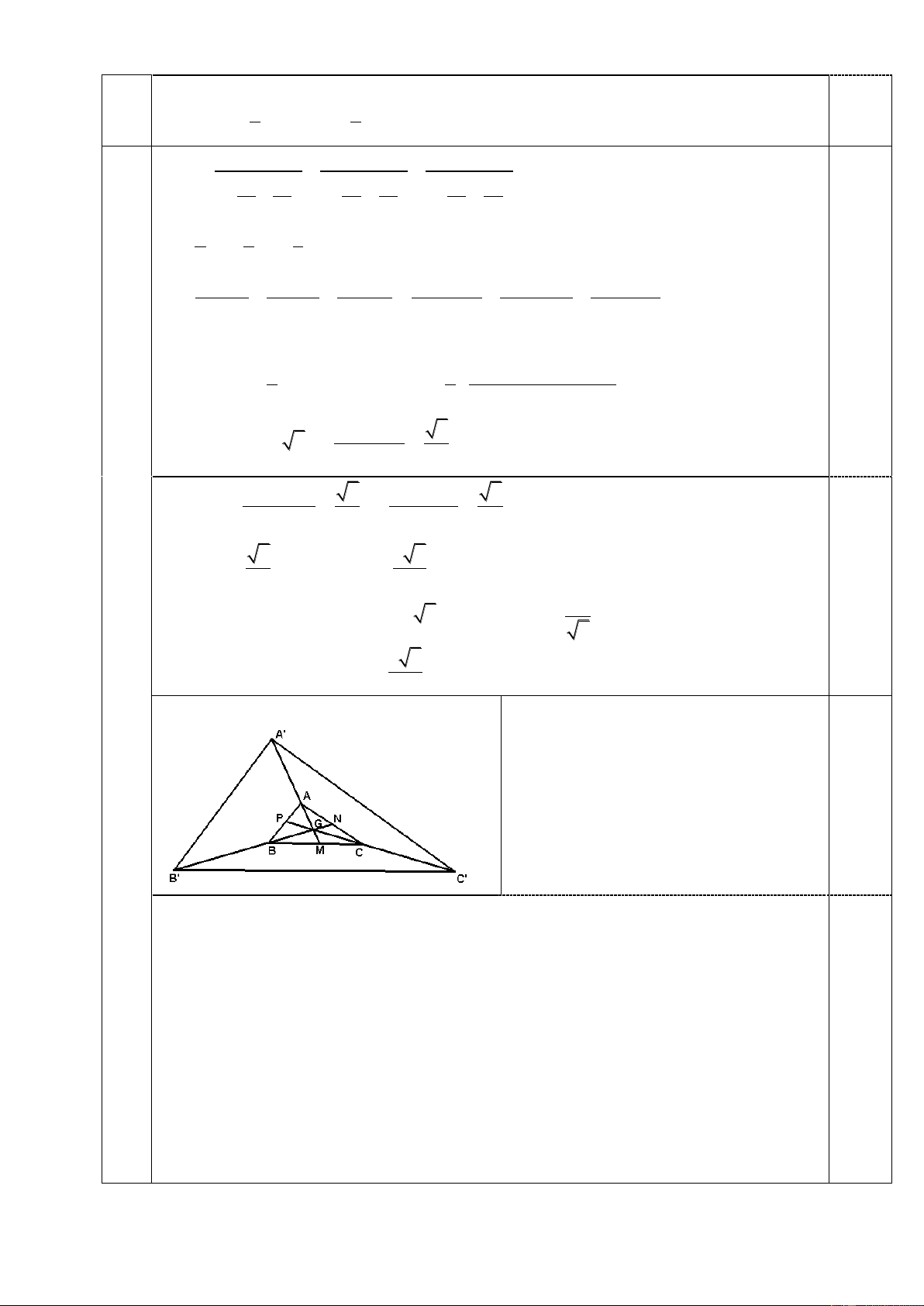
Lấy 5 điểm tùy ý sao cho không có ba
điểm nào thẳng hàng trên mặt phẳng. Khi
đó vì chỉ dùng hai màu để tô các đỉnh nên
theo nguyên lí Dirichlet phải tồn tại ba
điểm trong số đó cùng màu. Giả sử ba 0,5 điểm đó là , A ,
B C màu đỏ. Khi đó tam
giác ABC với ba đỉnh màu đỏ. Gọi G là trọng tâm tam giác .
ABC Khi đó chỉ có hai khả năng xảy ra
1. Nếu G màu đỏ thì , A ,
B C,G cùng màu và bài toán được chứng minh
2. Nếu G màu xanh, kéo dài G , A G ,
B GC và lần lượt lấy trên đó các điểm A', B ',C '
sao cho AA'  3G , A BB '  3G , B CC '  3G .
C Khi đó, nếu gọi M , N, P tương ứng là
trung điểm của BC,C ,
A AB thì AA'  3GA  6GM  AA'  2AM. Tương tự,
BB '  2AN,CC '  2C .
P Do đó các tam giác A' BC, B 'C ,
A C ' AB tương ứng nh n , A ,
B C làm trọng tâm. Mặt khác, các tam giác ABC và A' B 'C ' có cùng trọng tâm . G 0,5 Có hai trường hợp
2.1. Nếu A', B ',C ' có cùng màu xanh thì tam giác A' B'C ' và trọng tâm G cùng màu xanh
2.2. Nếu ít nhất một trong các điểm A', B ',C ' màu đỏ, không giảm tính tổng quát, giả sử
A' màu đỏ. Khi đó tam giác A' BC và trọng tâm A màu đỏ.
y trong mọi khả năng luôn tồn tại một tam giác có ba đỉnh và trọng tâm cùng màu.