Đề thi học sinh giỏi tỉnh Toán 9 năm 2020 – 2021 sở GD&ĐT Phú Yên

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH PHÚ YÊN
LỚP 9 THCS, NĂM HỌC 2020 - 2021 Môn thi: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 30/3/2021
Thời gian: 150 phút (không kể thời gian giao đề) ----------- Câu 1.(5,00 điểm) a) Chứng minh rằng: 3 3
5  2 13  5  2 13  1. b) Biết đa thức 4 3 2
x  4x  6 px  4qx  r chia hết cho đa thức 3 2
x  3x  9x  3 . Tính giá
trị biểu thức  p  q r .
Câu 2.( 3,50 điểm) Giải hệ phương trình:  xy 5   5  2 2x  y  xy  10 2x  y  xy   4.  xy
Câu 3.(2,50 điểm) Tìm nghiệm nguyên của phương trình: 2 2 2x  5y  13 .
Câu 4.(3,00 điểm) Cho tam giác nhọn ABC nội tiếp đường tròn (O). Tiếp tuyến tại B và C cắt
nhau ở D. Gọi E, F lần lượt là giao điểm của DA với (O) và DA với BC; H là giao điểm của OD với BC.
a) Chứng minh tam giác OAH đồng dạng với tam giác ODA.
b) Đường thẳng qua A song song với BC cắt (O) tại K (khác A). Chứng minh rằng E, H, K thẳng hàng.
Câu 5.(3,00 điểm) Tìm giá trị lớn nhất của biểu thức: 1  1 1  1 1 1 3 3
P  x  y với x  0, y  0,        2 2 xy  x y  x xy y
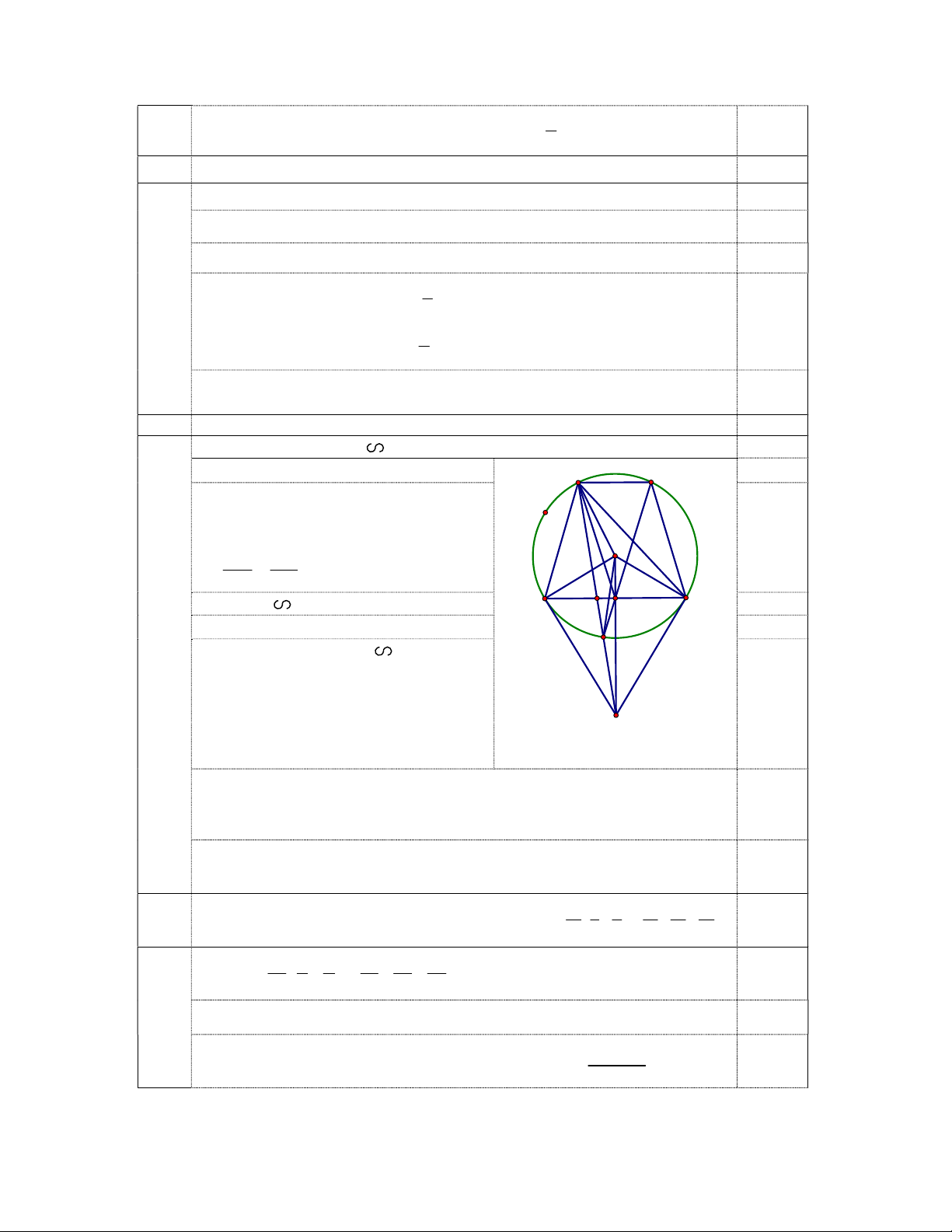
Câu 6.( 3,00 điểm) Cho tam giác ABC nhọn, có H là trực tâm, (I) là đường tròn nội tiếp. Gọi D,
E, F lần lượt là tiếp điểm của (I) với BC, CA, AB. Gọi K là hình chiếu vuông góc của D trên EF. a) Chứng minh rằng  FKB   EKC .
b) Gọi P, Q lần lượt là giao điểm của HB, HC với EF.
Chứng minh đẳng thức: EK.FP = FK .EQ.
c) Chứng minh rằng KD là phân giác của  HKI . ---------Hết---------
Thí sinh không sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ và tên thí sinh:………………………………………;Số báo danh:…………………….....…
Chữ kí giám thị 1:……….………………..;Chữ kí giám thị 2:………..………………………...
2. Đáp án và thang điểm CÂU ĐÁP ÁN ĐIỂM 1 5,00 đ a) Chứng minh rằng: 3 3
A  5  2 13  5  2 13  1. 2,50 đ Ta thấy: 3 A   3 3 10 9
5  2 13  5  2 13  109A 1,00 đ   A   2 1 A  A 10  0 . 0,50 đ 2  1  39 Vì 2 A  A 10  A    0  
nên suy ra A 1  0  A  1. 1,00 đ  2  4 b) Biết đa thức 4 3 2
x  4x  6 px  4qx  r chia hết cho đa thức 3 2
x  3x  9x  3 . Tính giá trị biểu thức Q   p  q r . 2,50 đ Giả sử 4 3 2
x  4x  6 px  4qx  r   x  a 3 2 x  3x  9x  3 0,50 đ 4  x  a   3 x   a   2 3 3
9 x  9a  3 x  3 . a 0,50 đ 4  a  3 a 1  6 p 3a 9     p  2
Đồng nhất các hệ số cùng bậc hai vế, ta được:    1,00 đ 4q  9a  3 q  3   r  3a r  3.
Suy ra  p  q r 15. 0,50 đ  xy 5   5  2 2x  y  xy 2
Giải hệ phương trình:  3,50 đ 10 2x  y  xy   4.  xy
Điều kiện xy  0, 2x  y  xy  0 . 0,25 đ
Đặt u  xy, v  2x  y  xy u,v  0 , hệ phương trình đã cho trở thành 0,50 đ u 5   5 (1) 2 v  10 v   4 (2).  u  Từ 10 u (2)  v  4  hay 4 10 v  . Thay vào (1) ta được 0,50 đ u u u 5u 
 5  u 10u  25  0  u 52 2
 0  u  5  v  2. 1,00 đ 2 4u 10 xy  5 xy  5
Ta được hệ phương trình:    0,50 đ 2x  y  xy  2 2x  y  7 x 1        y  x 7 2x 5 2 5 2x  7x  5  0       5 . y  7  2x  y  7  2x x  0,50 đ  2   y  2
Vậy hệ phương trình có hai nghiệm là    5  1;5 , ;2   . 0,25 đ  2  3
Tìm nghiệm nguyên của phương trình: 2 2 2x  5y  13 (*) 2,50 đ Ta có: (*) 2 2
 2(x 1)  5(3 y ) . 0,50 đ Do (2,5)  1 nên  2 x   1 5 và  2 3  y 2 . 0,50 đ Đặt 2 2
x 1  5k,3  y  2l , ta có: 10k  10l  k  l k,l  . 0,50 đ  1 2 k 
x  5k 1 0  Do đó: 5     k  l  1. 0,50 đ 2 y  3 2l  0 3 l    2 Vậy x  2  , y  1  . 0,50 đ
Phương trình có các nghiệm nguyên: (-2 ;-1), (-2 ;1), (2 ;-1) và (2 ;1). 4 3,00 đ a) Chứng minh ∆OAH ∆ODA 1,00 đ
Theo tính chất tiếp tuyến thì BC  OD . A K 0,25 đ
Áp dụng HTL vào tam giác vuông
OCD, với CH là đường cao ta có: 2 OC  OH.OD  2 OA  OH.OD 0,50 đ O OA OD   OH OA  B ∆OAH ∆ODA . F H C 0,25 đ
b) Chứng minh rằng E, H, K thẳng hàng 2,00 đ E
Từ câu a) ta có ∆OAH ∆ODA   OHA   OAD   OEA (1)  OAEH nội tiếp 1,00 đ D   EHD   EAO   OAD (2). Từ (1) và (2)   EHD   OHA (3).
Dễ thấy ∆ABH=∆KCH (c.g.c)  HA = HK hay AKH cân tại H (4).
Vì OH  BC, AK//BC  OH  AK (5). 0,50 đ
Từ (4) và (5) suy ra OH là phân giác  AHK hay  OHA   OHK (6).
Kết hợp (3) và (6) suy ra  OHK   EHD ; 0,50 đ Suy ra  EHO   OHK   EHO   0
EHD  180 , hay 3 điểm E, H, K thẳng hàng. 1 1 1 1 1 1 5 Tìm GTLN của biểu thức: 3 3
P  x  y với x0, y 0,        3,00 đ 2 2 xy x y x xy y 1  1 1  1 1 1 Giả thiết: 2 2      x  y  x  xy  y  
(do x  0, y  0 ). 0,50 đ 2 2 xy  x y  x xy y
Do đó: P  x  y   x  yx  xy  y    x  y2 3 3 2 2 . 0,50 đ x  y2
Để ý rằng x  y  x  xy  y   x  y2 2 2  3xy và xy  0,50 đ 4 3
Suy ra x  y   x  y2   x  y2   x  y x  y  4  0 0,50 đ 4 
Hay  x  y     x  y2 0 4 0  16. 0,50 đ
Vậy Max P = 16. Dấu đẳng thức xảy ra khi x  y  2. 0,50 đ 6 3,00 đ a) Chứng minh  FKB   EKC A 1,00 đ
Gọi M, N theo thứ tự là hình N chiếu của B, C lên EF. P E Khi đó: K  BFM   AFE   AEF   M F CEN 0,50 đ Q  BFM CEN I H BM BF BD     CN CE CD B D C
Mặt khác, BM//DK//CN nên theo định lí Thales ta có: BD MK BM MK      0,50 đ BMK CNK (c.g.c)   FKB   EKC . CD NK CN NK
b) Chứng minh đẳng thức: EK.FP = FK .EQ. 1,00 đ Dễ chứng minh được  BFP   CEQ,  FBP   ECQ (cùng phụ  BAC ). FB FP 0,50 đ Do đó BFP CEQ (g.g)   (1)  EC EQ Theo a)  FKB   EKC . Kết hợp với  BFK   CEK BFK CEK (g.g); FB FK 0,25 đ suy ra  (2)  EC EK FP FK Từ (1) và (2) suy ra   EK.FP  FK.EQ (đpcm). 0,25 đ EQ EK
c) Chứng minh KD là phân giác của  HKI 1,00 đ FP FK FP  FK KP EK FK EK  FK EF Theo b):        (3) 0,25 đ EQ EK EQ  EK KQ QK PK QK  PK QP
Hơn nữa, do IE//HP, IF//HQ, IE=IF nên  IEF   HPQ   IFE   HQP . 0,25 đ Do đó IEF HQP (g.g). IE EF Ta có IEF HQP   (4)  0,25 đ HQ QP EK IE Từ (3) và (4) ta có   IKE HKQ (c.g.c)   IKE   HKQ QK HQ 0,25 đ Suy ra  0 IKD    0 90 IKE  90   HKQ   HKD , hay KD là phân giác  IKH .