Đề thi học sinh giỏi tỉnh Toán 9 THCS năm 2018 – 2019 sở GD&ĐT Đăk Lăk

SỞ GIÁO DỤC & ĐÀO TẠO
KỲ THI HỌC SINH GIỎI TỈNH ĐĂK LĂK
NĂM HỌC 2018 – 2019
MÔN THI: TOÁN 9 – THCS ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Ngày thi: 10/4/2019 Bài 1: (4 điểm)
1) Rút gọn biểu thức A     3 3 2 3 33 12 5  37  30 3 . 
x x  6x 12 x  8  y y
2) Giải hệ phương trình 
x  2 x 1  2 y  Bài 2: (4 điểm) 1) Cho phương trình 2
x  4x  2 x  2  m  5 (với m là tham số). Tìm tất cả các giá trị của
m để phương trình đã cho có bốn nghiệm phân biệt.
2) Trong mặt phẳng với hệ tọa độ Oxy, một đường thẳng d có hệ số góc k đi qua điểm
M(0; 3) và cắt parabol P 2
: y  x tại hai điểm A, B. Gọi C, D lần lượt là hình chiếu vuông
góc của A, B lên trục Ox. Viết phương trình đường thẳng d, biết hình thang ABDC có diện tích bằng 20. Bài 3: (4 điểm)
1) Tìm tất cả các cặp số nguyên  ; x y  thỏa mãn: 2 2
2x  y  2xy  6x  4 y  20
2) Tìm tất cả các số tự nhiên có bốn chữ số, biết rằng số đó bằng lập phương của tổng các chữ số của nó.
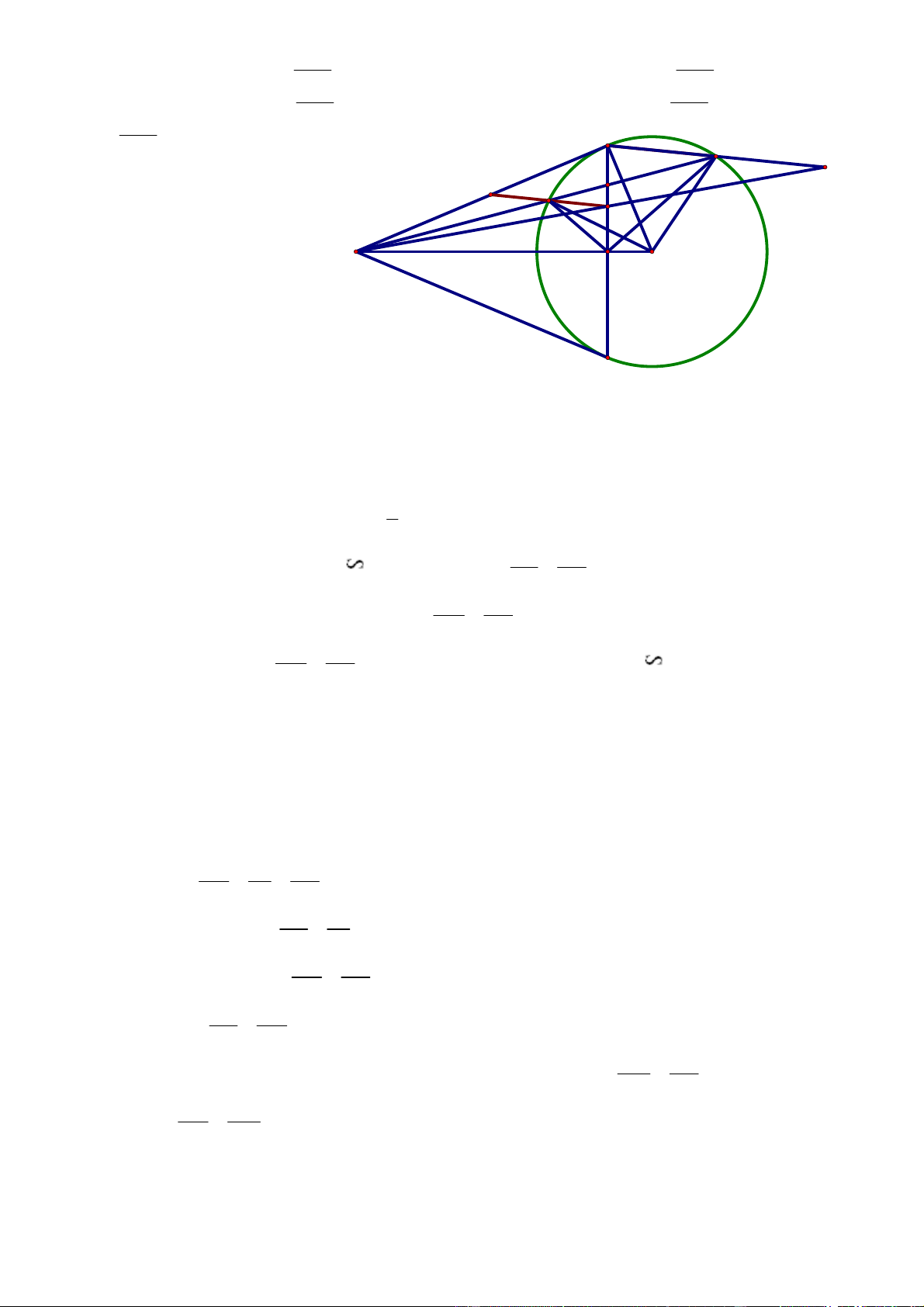
Bài 4: (4 điểm) Cho điểm A nằm ngoài đường tròn (O). Vẽ hai tiếp tuyến AB, AC (B, C
là tiếp điểm) và một cát tuyến ADE của (O) sao cho ADE nằm giữa hai tia AO và AB; D,
E  (O). Đường thẳng qua D và song song với BE cắt BC, AB lần lượt tại P, Q.
1) Gọi H là giao điểm của BC với OA. Chứng minh OEDH là tứ giác nội tiếp.
2) Gọi K là điểm đối xứng của B qua E. Chứng minh ba điểm A, P, K thẳng hàng.
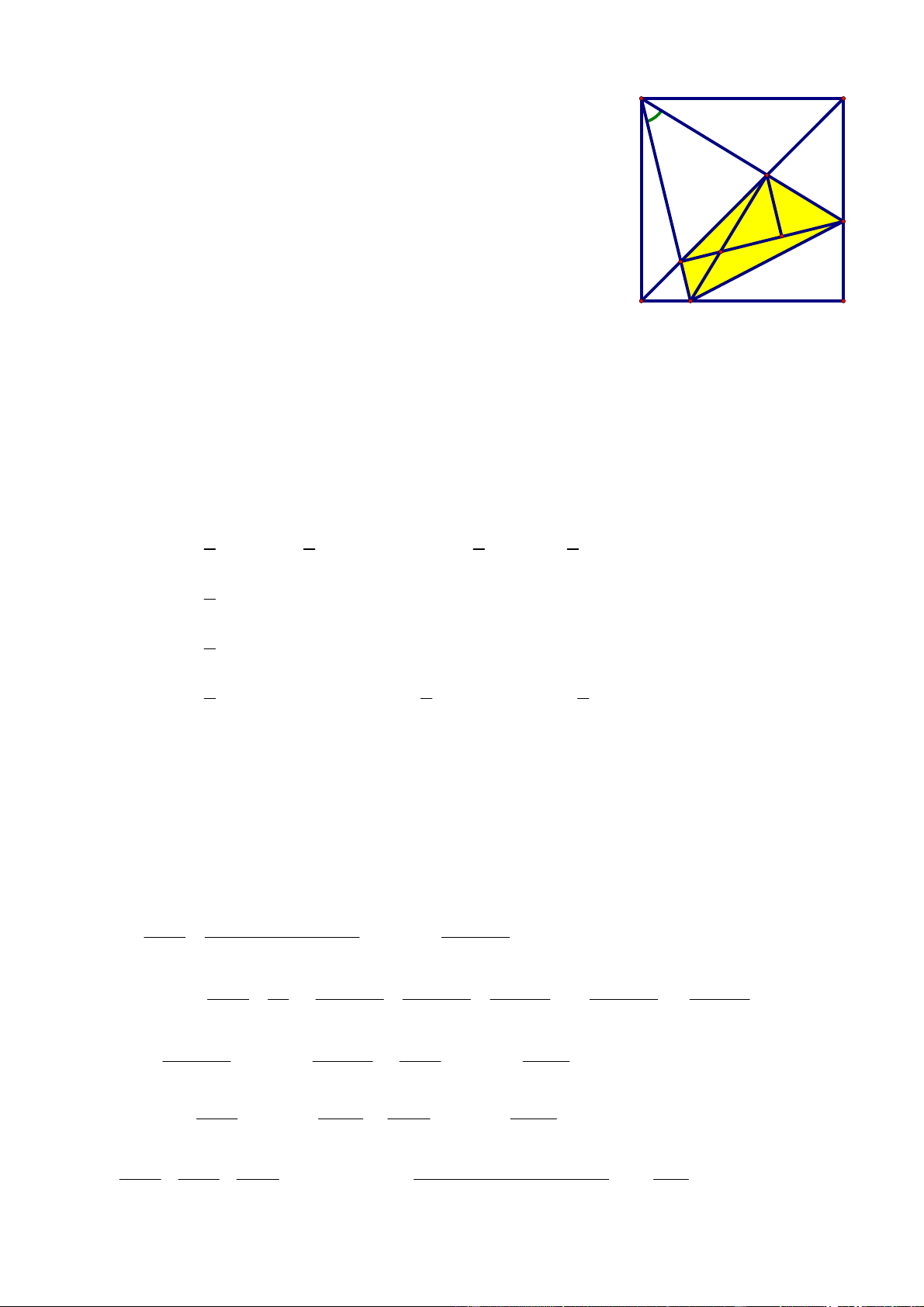
Bài 5: (2 điểm) Cho hình vuông ABCD. Trên các cạnh CB, CD lần lượt lấy các điểm M,
N (M không trùng với B và C; N không trùng với C và D) sao cho  0 MAN  45 . Chứng
minh rằng đường chéo BD chia tam giác AMN thành hai phần có diện tích bằng nhau.
Bài 6: (2 điểm) Cho , a ,
b c là các số thực dương thỏa a  b  c  3. Chứng minh rằng: a  1 b  1 c 1    3 2 2 2 b 1 c  1 a 1
-------------------- Hết --------------------
GV: Nguyễn Dương Hả
H i – THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm và
v giới thiệu) trang 1 BÀI GIẢI Bài 1: (4 điểm) 1) Ta có A                3 3 3 3 2 3 33 12 5 37 30 3 3 2 3 33 12 5 1 2 3              2 3 2 3 33 12 4 2 3 3 2 3 33 12 1 3  3 2 3  2112 3       2 3 2 3 3 2 3
 3  2 32 3  3  12  9  3
2) (ĐK: x  0, y  0 )
x x  6x  12 x  8  y y   
 x  3   y 3 2
 x  2  y    x  2  y       
x  2 x 1  2 y     
x  2 x 1  2 y 
 x  2 x 1  2 x  4 x 2 x 1 2 y  
 x  2  y        x  2 x 2 y  x  2  y  y    x 1  0         
 x  2 x 1  2 x  4 
x  4 x  3  0   x  
1 x 3  0  x  2  y    x  3  0   y  1  vo ly   x  1  x  9 x  9    
tm . Vậy nghiệm của hệ là    y  1  y  1  y  1      x  3   Bài 2: (4 điểm) 1) Ta có 2 2
x  4x  2 x  2  m  5  x  2  2 x  2  m 1  0 *
Đặt t  x  2 t  0 . Khi đó (*) trở thành: 2
t  2t  m 1  0 **
Do đó (*) có bốn nghiệm phân biệt  (**) có hai nghiệm dương phân biệt   0 1   m   t   1 0    m  0
  P  0   m 1  0    1   m  0 t m  1     S  0 2  0 t  
2) Vì đường thẳng d có hệ số góc k đi qua điểm M(0; 3), nên phương trình đường thẳng d
có dạng y  kx  3
Phương trình hoành độ giao điểm của (d) và (P) là: 2 2
x  kx  3  x  kx  3  0 *
Vì ac  3  0 , nên (*) luôn có hai nghiệm phân biệt
Vì (d) cắt (P) tại hai điểm A; B, nên hoành độ các điểm A, B là hai nghiệm của (*).
x  x  k Theo Vi ét ta có: A B 2 2 
. Lại có A x ; x , Bx ; x , C x ; 0, D x ; 0 A A B B A B  x x  3  A B 2
 AC  BDCD  2 2 x  x x  x  x x A B   A B  2 Do đó 20  S  
  x  x  A B   x  x ABDC A B  A B  2 2 2
Đặt t  x  x , ta có: A B 2 t  2 3 20 t t 6t 40 0 t 4t 4t 10 0
t 4 t 22 3 2 6                 0  t  4 . 2  
GV: Nguyễn Dương Hả
H i – THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm và
v giới thiệu) trang 2  t   x  x 
  x  x 2  x  x  x x  x  x 2 2 2 2 4 4 16 2
 2x x  2  3  k  6  6 A B A B A B A B A B A B 2
 k  4  k  2 . Vậy phương trình đường thẳng d là: y  2x  3 hoặc y  2  x  3 Bài 3: (4 điểm)
1) Ta có: x  y  xy  x  y 
  x  2   x  y  2 2 2 2 2 6 4 20 1 2  25 Vì      2   
  2   2 
  2   2 2 2 2 2 2 2 2 25 0 5 0 5 3 4 3 4 3 4 3 4 , nên có các trường hợp sau:  x 1  0 x  1   x  1  0  x  1   x  1  5  x  4 )    ; )    ; )    ;
x  y  2  5 y  4  
x  y  2  5 y  6   
x  y  2  0 y  6    x 1  5  x  6  x 1  3  x  2 x 1  4  x  3 )    ; )    ; )    ;
x  y  2  0 y  4  
x  y  2  4 y  0  
x  y  2  3 y  2   x 1  3  x  2 x 1  4   x  5  x 1  3  x  4  )    ; )    ; )   
x  y  2  4  y  8   
x  y  2  3 y  6  
x  y  2  4 y  6    x 1  4  x  3  x  1  3   x  4  x 1  4   x  5  )    ; )    ; )   
x  y  2  3 y  8   
x  y  2  4  y  2   
x  y  2  3 y  0   Vậy các cặp số  ; x y  là:  1
 ; 4 , 1;  6, 4;  6,  6
 ; 4, 2; 0, 3;  2, 2;  8,  5  ; 6, 4; 6
3;  8, 4;  2,  5  ; 0 Cách khác: 2 2 2
x  y  xy  x  y 
 x    y  2 2 2 6 4 20 2 2 3
x  y  4 y  20  0 *
(*) có nghiệm      y2   2 y  y   2 2 3 2 4
20  0   y  2 y  49  0  y  2 y  49  0   y  2 1
 50  y 1  5 2  1
  5 2  y  1 5 2  8
  y  6 (vì y  Z ) (*) có nghiệm nguyên 2 2
    y  2 y  49  k k  N   y  8  ;  6;  2; 0; 4; 6  x  2
+) Với y  8; * 2 2
 2x 10x 12  0  x  5x  6  0   x  2 x  3  0   x  3   x  1 
+) Với y  6; * 2 2
 2x  6x  8  0  x  3x  4  0   x 1 x  4  0  x  4   x  3
+) Với y  2; * 2 2
 2x  2x  24  0  x  x 12  0   x  3  x  4  0  x  4    x  5
+) Với y  0; * 2 2
 2x  6x  20  0  x  3x 10  0   x  5 x  2  0  x  2   x  1 
+) Với y  4; * 2 2
 2x  14x 12  0  x  7x  6  0   x 1 x  6  0  x  6    x  4 
+) Với y  6; * 2 2
 2x  18x  40  0  x  9x  20  0   x  4 x  5  0  x  5  
2) Gọi abcd là số tự nhiên phải tìm 1000  abcd  9999
Ta có abcd  a  b  c  d 3 
 a  b  c  d 3 1000
 9999  10  a  b  c  d  21
+) Nếu a  b  c  d  10  abcd  1000 loai ; +) Nếu a  b  c  d 11 abcd  1331loai ;
+) Nếu a  b  c  d  12  abcd  1728 loai ; +) Nếu a  b  c  d  13  abcd  2917 loai ;
+) Nếu a  b  c  d  14  abcd  2744 loai ; +) Nếu a  b  c  d  15  abcd  3375 loai ;
+) Nếu a  b  c  d  16  abcd  4096 loai ; +) Nếu a  b  c  d  17  abcd  4913 nhan ;
GV: Nguyễn Dương Hả
H i – THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm và
v giới thiệu) trang 3
+) Nếu a  b  c  d  18  abcd  5832 nhan ; +) Nếu a  b  c  d  19  abcd  6859 loai ;
+) Nếu a  b  c  d  20  abcd  8000 loai ; +) Nếu a  b  c  d  21 abcd  9261loai . B
Vậy abcd  4913; 5832 . E K Bài 4: (4 điểm) I K' Q D P A H O
1) Chứng minh OEDH là tứ giác nội tiếp. C
Ta có: AB = AC (AB, AC là hai tiếp tuyến của (O)), OB = OC (bán kính)
Nên OA là trung trực của BC Xét ABO:  0
ABO  90 (AB là tiếp tuyến của (O)), BH  OA (OA là trung trực của BC) 2
 AB  AH.AO a 1 Xét ABD và AEB:    ABD  AED 
sd BD (góc nội tiếp, góc tạo bởi tia tiếp tuyến và dây) 2  AB AD
BAD (góc chung). Vậy ABD AEB (g.g)  2 
 AB  AD.AE b AE AB AH AE
Từ (a) và (b) suy ra  AH.AO  A . D AE   AD AO AH AE Xét AHD và AEO:  cmt  , 
HAD chung  . Vậy AHD AEO (c.g.c) AD AO  
 AHD  AEO . Do đó tứ giác OEDH là tứ giác nội tiếp (đpcm)
2) Chứng minh ba điểm A, P, K thẳng hàng.
Ta có: ODE cân tại O (do OD = OE)  
 EDO  AEO mà   AHD   
AEO cmt   EDO  AHD Lại có:  
EDO  EHO (tứ giác OEDH nội tiếp)   0  0       
 AHD  EHO  90  AHD  90  EHO  BHA  AHD  BHO  EHO  BHD  BHE
Nên HB là phân giác trong của DHE, mà HA  HB (cmt) nên HA là phân giác ngoài HD ID AD của DHE   
c (I là giao điểm của HB và DE) HE IE AE DP ID DIP, DP // BE (gt)  
d  (hệ quả Ta Lét) BE IE DQ AD ABE, DQ // BE (gt)  
e (hệ quả Ta Lét) BE AE DP DQ Từ c), d), e)    DP  DQ . BE BE DP AD
Gọi K’ là giao điểm của AP và BE. AEK’, DP // EK’ (gt)    f  EK  AE DQ DP Từ e), f)  
mà DP  DQ cmt   BE  EK BE EK 
Mặt khác BE  EK  gt  K  K . Vậy A, P, K thẳng hàng (đpcm).
GV: Nguyễn Dương Hả
H i – THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm và
v giới thiệu) trang 4 Bài 5: (2 điểm) A B Tứ giác ABMF: 450  0
MAF  45  gt  ,  0
MBF  45 (BD là đường chéo hình vuông) E
Vậy tứ giác ABMF nội tiếp  0  0 0 0
 AFM  180  ABM  180  90  90 AFM:  0  0 M
AFM  90 , FAM  45 , K F H
nên AFM vuông cân tại F  AF = MF
Tương tự AENvuông cân tại E  AE = NE D N C Tứ giác AEHF:   0
AFH  AEH  90 cmt  (H là giao điểm của MF và NE)
nên tứ giác AEHF nội tiếp    0
 NHF  MHE  EAF  45
Kẻ EK  MF (K  MF). NFH vuông tại F; EKH vuông tại K nên có:  0  0
NF  NH  sin NHF  NH  sin 45 ,
EK  EH  sin MHE  EH  sin 45 Ta có: S  S  S  S  S MNFE MHN NHF FHE EHM 1 1  1 1   HM  NF 
HN  HF  sin NHF  HF  EK 
HM  HE  sin MHE 2 2 2 2 1   0 0 0 0
HM  HN  sin 45  HN  HF  sin 45  HF  HE  sin 45  HM  HE  sin 45  2 1 
 HM  HF   HN   HF  HM  0  HE   sin 45 2   1 1 1 
MF   HN  HE  0 0 0  sin 45 
MF  NE  sin 45 
AF  AE  sin 45  S 2 2 2 AEF
Bài 6: (2 điểm) Ta chứng minh a  b  c2  3ab  bc  ca * . Thật vậy   2 2 2
 a  b  c  ab  bc  ca    2 2 2 * 0
2 a  b  c  ab  bc  ca   0
 a  b2  b  c2  c  a2  0 (luôn đúng). Dấu “=” xảy ra  a  b  c Áp dụng (*), ta có: 2
3  3ab  bc  ca  ab  bc  ca  3 a 1 a   1  2 b   2 1  b    a   2 1 b Lại có:   a  1  2 2   2 b 1 b 1 b  1 1 1 a   2 1 b a   2 1 b a   1 b a   2 1 b a 1 b 2  
Vì b 1  2b          2 2 2 b 1 2b b 1 2b 2 b 1 2 a   2 1 b a   1 b a 1 ab  b  a   1   a 1    a 1  do b  0 2   2     b  1 2 b 1 2 b  1 bc  c c 1 ca  a Tương tự có:  b 1  ;  c  1  2   2   c 1 2 a  1 2 a 1 b 1 c 1
ab  bc  ca  a  b  c 3  3 Vậy  
 a  b  c  3   6   3 2 2 2   b 1 c 1 a 1 2 2
Dấu “=” xảy ra a  b  c  1.
GV: Nguyễn Dương Hả
H i – THCS Nguyễn Chí Thanh – BMT – Đăk Lăk (Sưu tầm và
v giới thiệu) trang 5