Đề thi học sinh giỏi Toán 7 năm 2020 – 2021 phòng GD&ĐT Trực Ninh – Nam Định

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI HUYỆN TRỰC NINH NĂM HỌC 2020-2021 MÔN TOÁN LỚP 7 (Đề thi gồm 01 trang)
(Thời gian làm bài 120 phút, không kể thời gian giao đề) ĐỀ CHÍNH THỨC Câu 1(4 điểm). 10 10 7.14 .2  1024.21.7
a) Tính giá trị biểu thức: A  8 9 5 6 10.2 .7 .98  28 .7  1   1   1   1   1  b) Tính: B  1 . 1 . 1 ... 1 . 1            4   9  16  100  121 
c) Tìm x biết: x 1  x  2  x 3 ... x 100  605x Câu 2 (4 điểm). 2x 1 3y  2 a) Tìm x, y biết :  và x  y  2 5 3
b) Cho a, b, c là các số thực khác 0. Tìm các số thực x, y, z khác không 2 2 2 xy yz zx x  y  z thỏa mãn:    2 2 2 ay  bx bz  cy cx  az a  b  c Câu 3 (2 điểm) 2021 10  539 a) Chứng minh rằng
có giá trị là một số tự nhiên. 9
b) Chứng minh đa thức sau không có nghiệm 12 9 8 7 6 3
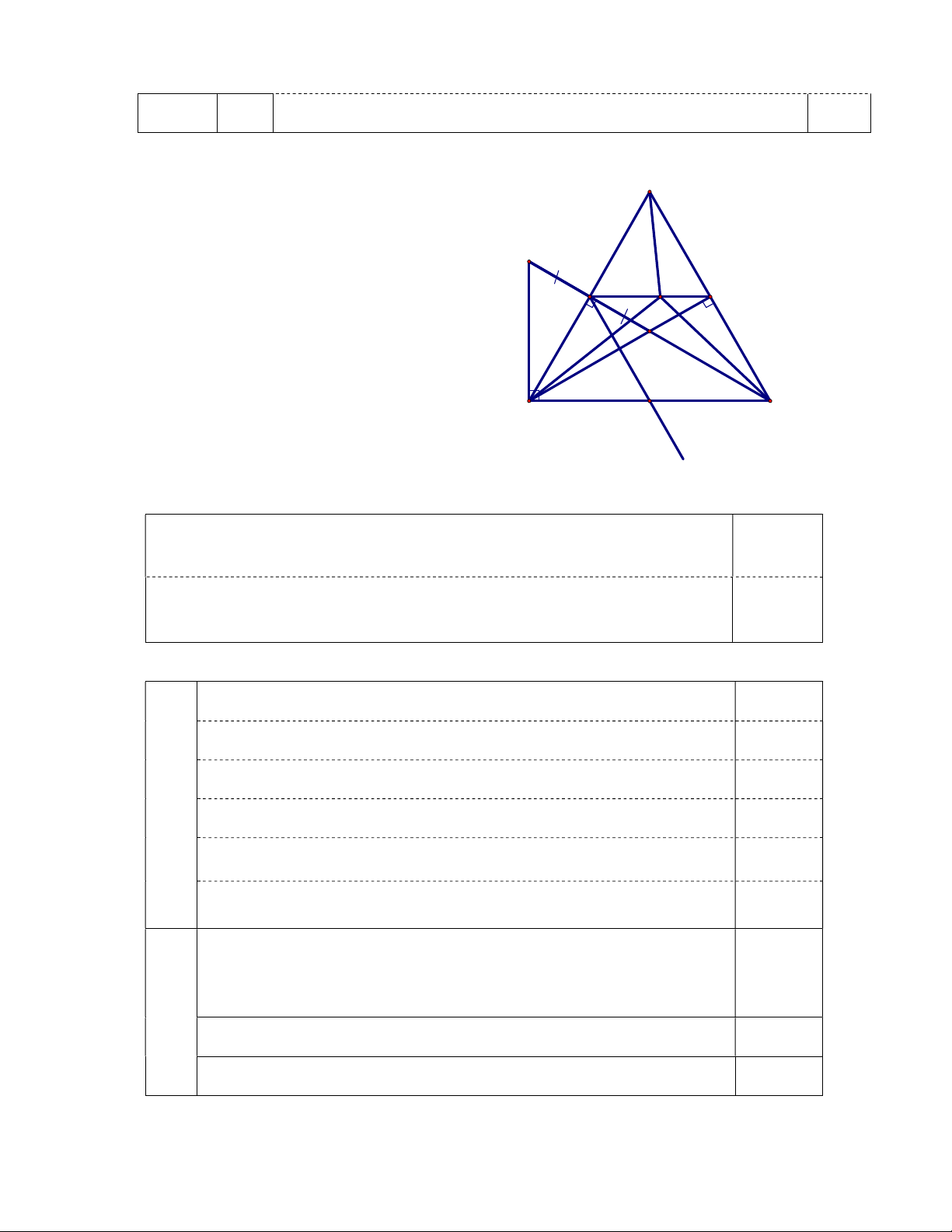
A  x  x  x  x  x  x 1 Câu 4 (8,0 điểm) Cho A  BC vuông tại A có  B  2
C. Kẻ AH  BC(H  BC) . Trên tia
HC lấy D sao cho HD  HB . Từ C kẻ đường thẳng CE vuông góc với đường thẳng AD (E  AD) .
a) Tam giác ABD là tam giác gì? Vì sao?
b) Chứng minh DH  DE; HE / / AC c) So sánh 2 HE và 2 2 (BC  AD ) : 4
d) Gọi K giao AH và CE , lấy điểm I bất kì thuộc đoạn thẳng HE  3
I khác H ; I khác E  . Chứng minh AC  IA  IK  IC 2 Câu 5 (2 điểm)
Tìm x nguyên biết : x 1  x  2  x 3 ... x 90  2025
_____________Hết_____________
HÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM THI CHỌN HỌC SINH GIỎI HUYỆN TRỰC NINH NĂM HỌC 2020-2021 MÔN TOÁN LỚP 7
(Thời gian làm bài 120 phút, không kể thời gian giao đề) Câu Ý Hướng dẫn Điểm Câu 1 10 10 10 10 10 7.14 .2 1024.21.7 7.(2.7) .2  2 .3.7.7 (4  8 9 5 6 8 9 2 2 5 6 điểm) 10.2 .7 .98  28 .7 5  .2.2 .7 .2.7  0,5 (2 .7) .7 10 10 10 10 11 11 10 11 7.2 .7 .2  2 .3.7.7 2 .7  2 .3.7 a   8 9 2 2 5 6 10 11 10 11 5  .2.2 .7 .2.7  (2 .7) .7 5  .2 .7  0,5 2 .7 10 11 2 .7 (2  3)  5   0,25 10 11 2 .7 ( 5  1) 4  1   1   1   1   1  3 8 15 9  9 1  20 1 . 1 . 1 ... 1 . 1  . . ... .            4   9  16  100  121  4 9 16 100 121 0,5
Nhận xét: Tích trên có chẵn các thừa số âm b 3.8.15...99.120 1.3.2.4.3.5...9.11.10.12   0,5
4.9.16...100.121 2.2.3.3.4.4...10.10.11.11 1.2.3...9.10 3.4.5...11.12 1 12  .  . 6  0,5
2.3.4...10.11 2.3.4...10.11 11 2 11  x 1 0; x x2 0; x Vì  .  ..................... x100 0; x  0,25
 x 1  x  2  x 3 ... x 100  0 ;x
Mà x 1  x  2  x  3 ... x 100  605x  605x  0 c  x 0x1x1 x2 x2 Khi đó  0,25 .  ..................... x100 x100 
Ta có x 1 x  2  x  3  ...  x 100  605x 0,25 (1100).100 100x   605x 0,25 2 (1100).100 100x   605x 2  505x=5050 0,25  x=10 KL: Câu 2
Áp dụng tính chất dãy tỉ số bằng nhau ta có (4 2x 1 3y  2 6x  3 6y  4
6x  3  6 y  4 6(x  y)  7 điểm)  =    0,5 5 3 15 6 15  6 21 6.2  7 5   (vì x + y = 2) 0,25 21 21 2x 1 5  23  x  a  5 21 42x  21  25 42x  46  21        0,5 3y  2 5  63y  42 15 63y  57 57   y   3 21  63  23 x   Vậy 21  0,25 57 y   63 xy yz zx Từ   ay  bx bz  cy cx  az xyz yzx zxy 0,25    ayz  bxz bzx  cyx cxy  azy
(vì x, y, z là các số khác 0) ayz  bxz  bzx  cyx b  zx  y c x  cxy  azy 0,25 ayz  bxz  cxy  azy  b ayz  y c x az  x c    b  zx  azy  b
 x  ay (vì x, y, z là các số khác 0) 0,25 b  xz cxy b   z  cy    x z  a c   y x x y z       0,25 b a a b c   z y  c b x  ak x y z  Đặt 
  k (k  0)  y  bk thay vào đề bài ta có 0,25 a b c z  ck  2 2 2 ak.bk (ak)  (bk)  (ck)  2 2 2 abk  bak a  b  c 0,5 2 2 2 2 k k (a  b  c ) 2    k 2 2 2 2 a  b  c 2 1
k  2k  k(1 2k)  0  k  vì k  0 0,5 2  1 x  a  2   1  y  b 0,25đ 2   1 z  c  2 2021 10  539 Chứng minh rằng
có giá trị là một số tự nhiên. 9 0,25 2021 10
 539 100...00000  539 100...00539 Ta có   a 9 9 9
Trong đó số 100…00539 là số có tổng các chữ số chia hết cho
9 nên số đó chia hết cho 9. 2021 10  539 0,5 Vậy
có giá trị là một số tự nhiên 9 12 9 8 7 6 3        Câu 3 A x x x x x x 1 Ta có x12; x8; x6 (2  0 với mọi x (*) 0.25 điểm) 12 9 12 9 x  x  x  x  0   +) Nếu x  1 khi đó 8 7 8 7
x  x   x  x  0  suy ra 0,25 6 3  6 3 x x x x 0       b 12 9 8 7 6 3
A  x  x  x  x  x  x 1  1>0
+) Nếu x  0 khi đó –x9; -x7; -x3  0 kết hợp với (*) ta có 0,25 12 9 8 7 6 3
A  x  x  x  x  x  x 1  1>0
+) Nếu 0 < x < 1 ta có 12 9 8 7 6 3
A  x  x  x  x  x  x 1= 12 8 9 6 7 3
x  x  x  x  x 1 x = 12 8 6 3
x  x (1 x)  x (1  x) 1 x 0,25
Vì 0 < x < 1 nên 1-x >0, 1-x3 > 0 kết hợp với (*) suy ra 12 9 8 7 6 3
A  x  x  x  x  x  x 1>0
Vậy đa thức đã cho không có nghiệm với mọi x 0,25
Câu 4 (8,0 điểm) Hình vẽ: K B H I E D A M C x
Câu a) ABD là tam giác gì? Vì sao? (1,5 điểm)
Chứng minh ABD có đường vuông góc AH đồng thời là đường trung 0,75
tuyến ứng với cạnh BD suy ra ABD cân tại A Tính được góc  0
B  60 suy ra ABD cân có một góc bằng 0 60 là tam 0,75 giác đều.
Câu b) Chứng minh DH  DE , HE / / AC (2,5 điểm) Tính được  0 C  30 (1) 0,25 Tính được  0 CAD  30 (2) 0,25
Từ (1) và (2) suy ra ADC cân tại D 0,25 1,5 Suy ra DA  DC 0,25
Chứng minh được AHD  C
 ED (cạnh huyền - góc nhọn) 0,25 Suy ra DH  DE 0,25 Tính được  0 ADC 120 Ta có  ADC   HDE (đối đỉnh) 0,25 Suy ra  0 HDE 120 Tính được  0 DHE  30 (3) 0,25 1,0 Từ (1), (3) suy ra  ACD   DHE 0,25 Ta có  ACD   DHE (cmt)    HE / / AC 0,25
mµ hai gãc nµy ë vÞ trÝ so le trong
(Dấu hiệu nhận biết hai đường thẳng song song)
Câu c) (2,0 điểm) So sánh 2 HE và 2 2 (BC  AD ) : 4
Chứng minh AHE cân tại H (tam giác có 2 góc bằng 0 30 0,5 Suy ra HA  HE (4) Trong góc 
AHC kẻ tia Hx cắt AC tại M sao cho  0 AHM  60 Chứng minh được H  MC cân tại M 0,25 Suy ra MH  MC (5) Chứng minh được A  HM đều 0,25 Suy ra AH  HM  MA (6) 2 Từ (4), (5) và (6) suy ra AC  AC 2  HE   HE    0,25 2  2  2 2 2 2 2 Ta có lại có BC  AD AB  AC  AD  (vì 2 2 2 BC  AB  AC ) 4 4 0,5 2 2 AC  AC      (Vì 2 2 AB  AD ) 4  2  2 2 Suy ra BC  AD 2 HE  0,25 4
Câu d) (2 điểm) Chứng minh 3 AC  IA  IK  IC 2
Chứng minh KAC đều (tam giác có 2 góc bằng 0 60 ) 0,5 Suy ra AK  KC  AC
Xét IKA có IK  IA  AK (bất đẳng thức  ) Xét I
 KC có IK  IC  KC (bất đẳng thức  ) 0,5  Xét I
 CA có IC  IA  AC (bất đẳng thức  )
Suy ra IK  IA  IK  IC  IC  IA  AK  KC  AC 0,5
=> 2.IA 2.IK  2.IC  3.AC (vì AC  AK  KC )
=> 2.(IA  IK  IC)  3.AC 0,5 => 3
IA  IK  IC  AC . Vậy 3 .AC  IA  IK  IC (ĐPCM) 2 2
Câu 5. Tìm x nguyên sao cho: x 1  x 2  x 3 ... x 90  2025
Câu 5 x 1  x 1 ;x  (2,0  điểm)
x  2  x  2 ;x  ..........................   x  45  x  45 ; x   0,25
x  46  46 x ;x
x  47  47 x ;x  ........................... 
x 90 90 x ;x
 x 1  x  2  x  3  ...  x  90  0,25đ
x 1 x  2  ...  x  45  46  x  47  x  ...  90  x ; x  (1 45).45 (46  90).45
 x 1  x  2  x  3  ...  x  2020    2 2 0,5đ
 x 1  x  2  x  3  ...  x  90  2025
Dấu bằng xảy ra khi và chỉ khi x 1  x 1  x10    x 2 x 2      x   2 0    ..........................    .............    x  45  x  45  x   450     45 x  46 x  46  46 x  x  46  0       x     47 0 x 47 47 x      0,5  .............. 
...........................       x     90 0 x 90 90 x  
Mà x là số nguyên suy ra x45;;4  6 0,5đ
Chú ý: - Học sinh làm cách khác đúng vẫn cho điểm tối đa.