Đề thi học sinh giỏi Toán 9 cấp tỉnh năm 2016 – 2017 sở GD&ĐT Lai Châu

UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2016-2017 Môn thi: Toán ĐỀ THI SỐ 1
Thời gian: 150 phút (không kể thời gian phát đề)
(Đề thi có 01 trang)
Ngày thi: 9/4/2017 Câu 1: (4,0
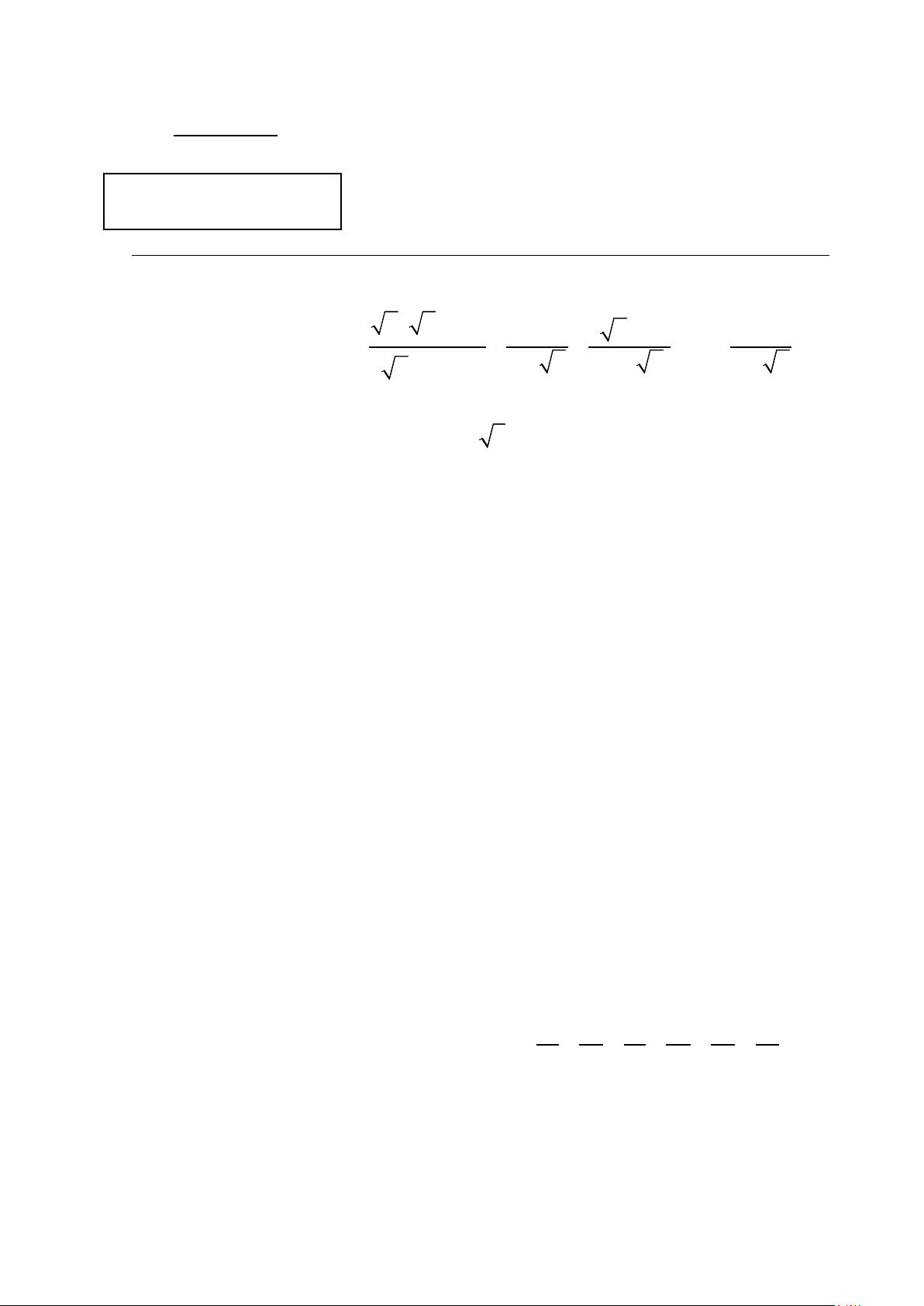
điểm)   x ( x 2)2  +
Cho biểu thức: P = 4 8 x + 32  2  x x x x  ( x + ) − + :1− 2 + 2 8  − −  2   1 3 +   a) Rút gọn P;
b) Tính giá trị của P với x = 9 − 4 5 ;
c) Tìm các giá trị chính phương của x để P có giá trị nguyên.
Câu 2: (4,0 điểm)
2.1. Chứng minh với mọi n là số tự nhiên chẵn thì 20n + 16n - 3n - 1  323
2.2. Tìm các số nguyên x,y thỏa mãn: 2x2 + y2 + 3xy + 3x + 2y + 2 = 0
Câu 3: (4,0 điểm)
3.1. Cho phương trình: x2 - (m + 5)x + 3m + 6 = 0. Tìm m để phương trình
có hai nghiệm x1, x2 là độ dài hai cạnh tam giác vuông có cạnh huyền bằng 5. 2 2
y + xy = 6x
3.2. Giải hệ phương trình sau:  2 2 2 1
 + x y = 5x
Câu 4: (6,0 điểm)
Cho đường tròn (O). Qua điểm A nằm ngoài đường tròn kẻ hai tiếp tuyến
AM, AN (M, N là hai tiếp điểm) và cát tuyến ABC với đường tròn (B nằm giữa
A và C). Gọi I là trung điểm của BC.
a) Chứng minh: A, M, O, I, N thuộc một đường tròn;
b) Chứng minh: IA là tia phân giác của  MIN ;
c) Vẽ dây CD song song MN, H là giao điểm của BD và MN. Chứng minh: HM = HN.
Câu 5: (2,0 điểm) Cho x, y, z > 0 và x + y + z = 1.
Tìm giá trị nhỏ nhất của biểu thức: Q = 1 1 1 1 1 1 + + + + + 2 2 2 x y z xy yz xz
--------------------Hết------------------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm. Trang 1/1. UBND TỈNH LAI CHÂU
KỲ THI CHỌN HỌC SINH GIỎI LỚP 9 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2016-2017 HƯỚNG DẪN CHẤM Môn: Toán ĐỀ THI SỐ 1 (Gồm: 05 trang)
Thời gian: 150 phút (không kể thời gian phát đề)
Ngày thi: /4/2017
Người ra đề: Chung HƯỚNG DẪN CHẤM Câu Ý Đáp án Thang điểm
ĐKXĐ của P là : x > 0 và x ≠ 4 0,25
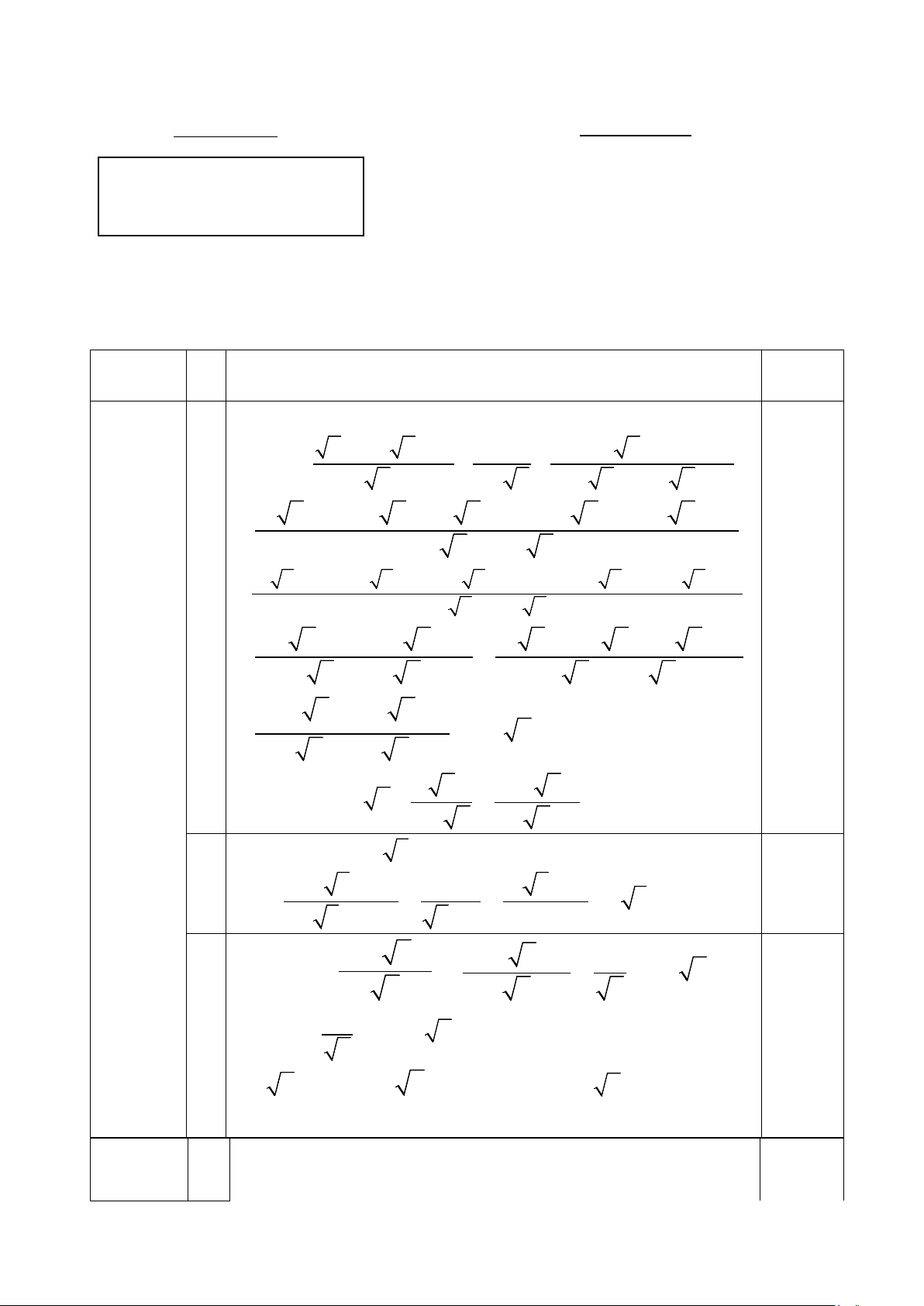
x(x + 4 x + 4) 4 8 x + 32 Đặt: A = − + x + 2 x +1+ 3
2 − x (2 − x)(4 + 2 x + x) 0,5
(x x + 4x + 4 x)(2 − x) − 4(x + 2 x + 4) + 8 x + 32 = (2
− x)(x + 2 x + 4) 3 2 3
2( x) + 8x + 8 x − x − 4( x) − 4x − 4x −8 x −16 + 8 x + 32 = 0,25 a
(2 − x)(x + 2 x + 4) 3 2 3 2( −
x) − x + 8 x +16 −( x) (2 + x) + 8( x + 2) = = 0,25 (2
− x)(x + 2 x + 4)
(2 − x)(x + 2 x + 4) 3 (2 + x) 8  − ( x)    Câu 1 = = 2 + x (2 0,25
− x)(4 + 2 x + x) (4 điểm) 2 x (2 + x) Vậy: P = (2 + x) : =
(x > 0 và x ≠ 4 ) 0,5 2 + x x
Thay x = 9 − 4 5 vào P ta được : b 2 (2 + 5 − 2) 5 5( 5 − 2) 0,5 P = = = = 5 5 −10 5 − 2 5 − 2 5 − 4 2 (2 + x) 4 + 4 x + x 4 Ta có: P = = = + 4 + x x x x 0,5
c P ∈ Z ⇔ 4 ∈ Z và x ∈Z 0,25 x
⇔ x ∈Ư (4) ⇔ x ∈{ 1 ± , 2 ± ,± } 4 và x ∈Z 0,25
⇔ x = 1 hoặc x = 16 thì P có giá trị nguyên. 0,5
Ta thấy 323 = 17.19 mà (17; 19) = 1 ta chứng minh
Xét B =20n +16n − 3n −1  17 và B  19 0,5 Trang 1/5.
ta có B = (20n - 3n) + (16n - 1)
có 20n - 3n = (20 - 3)M = 17M  17 2.1 0,5
16n - 1 = (16 + 1)N = 17N  17 ( n chẵn) ⇒ B  17 (1)
ta có: B = (20n - 1) + (16n - 3n) Câu 2
có 20n - 1 = (20 - 1)P = 19P  19 (4 điểm)
có 16n - 3n = (16 + 3)Q = 19Q  19 ( n chẵn) 0,5 ⇒ B  19 (2)
Từ (1) và (2) ⇒ B  323 0,5
2x2 + y2 + 3xy + 3x + 2y + 2 = 0
⇔ (2x + y + 1)(x + y + 1) = -1 0,5
⇒ 2x + y + 1 và x + y + 1 là các ước của -1 0,25 2.2 2x + y +1 = 1 x = 2 0,5 TH1:  ⇒ 
x + y +1 = −1 y = 4 −
2x + y +1 = −1 x = -2 TH2:  ⇒  0,5 x + y +1 = 1 y = 2
Kết luận (x,y) ∈{(2; - 4), (-2; 2)} 0,25
Phương trình có hai nghiệm x1, x2 là độ dài hai cạnh của
tam giác ⇒ Phương trình phải có hai nghiệm dương 0,25 2 2
(m + 5) − 4(3m + 6) ≥ 0 (m −1) ≥ 0  m 5 0  ⇔ + > ⇔ m > 5 − ⇔ m > 2 − 0,75   3.1 3m + 6 > 0 m > 2 −  
- Vì x1, x2 là độ dài hai cạnh của tam giác vuông có cạnh huyền bằng 5 nên: 2 2 2
x + x = 25 ⇔ (x + x ) − 2x x = 25 0,25 1 2 1 2 1 2
- Áp dụng định lí Vi-et ta được: 0,5
(m + 5)2 - 2(3m + 6) = 25 ⇔ m2 + 4m - 12 = 0 3
⇔ m = -6(loại); m = 2(thỏa mãn). Vậy m = 2. 0,25 (4điểm) y = 0 - Nếu x = 0 ⇒ (vô lí) 1   = 0 0,25
- Vậy x ≠ 0, khi đó chia hai vế của từng phương trình của hệ với x2 ta được: 3.2 2   1  1 y y . y .  + y = + =    6  6 2  x x  x  x   ⇔  0,25 2  1 2   1  1 + y = 5 + y − y = 2   2. . 5  x   x  x Trang 2/5.  1 S = +  y S.P = 6 Đặt:  x 
(ĐK: S2 ≥ 4P) khi đó: 1  0,25  2 P = . S − 2P = 5  y  x S.P = 6 S.P = 6 ⇔  ⇔ 0,25 3  2
S − 5S −12 = 0
(S − 3)(S + 3S + 4) = 0 S.P = 6 S = 3 TH1: 1  ⇔
⇒ và y là nghiệm của phương S 3 0  − = P = 2 x 0,25 trình: X2 - 3X + 2 = 0 x =1, y = 2 ⇔ X =1, X = 2  ⇒ 1 2 1  0,25 x = , y =1  2 S.P = 6 TH2:  (Vô nghiệm) 0,25 2 S  + 3S + 4 = 0
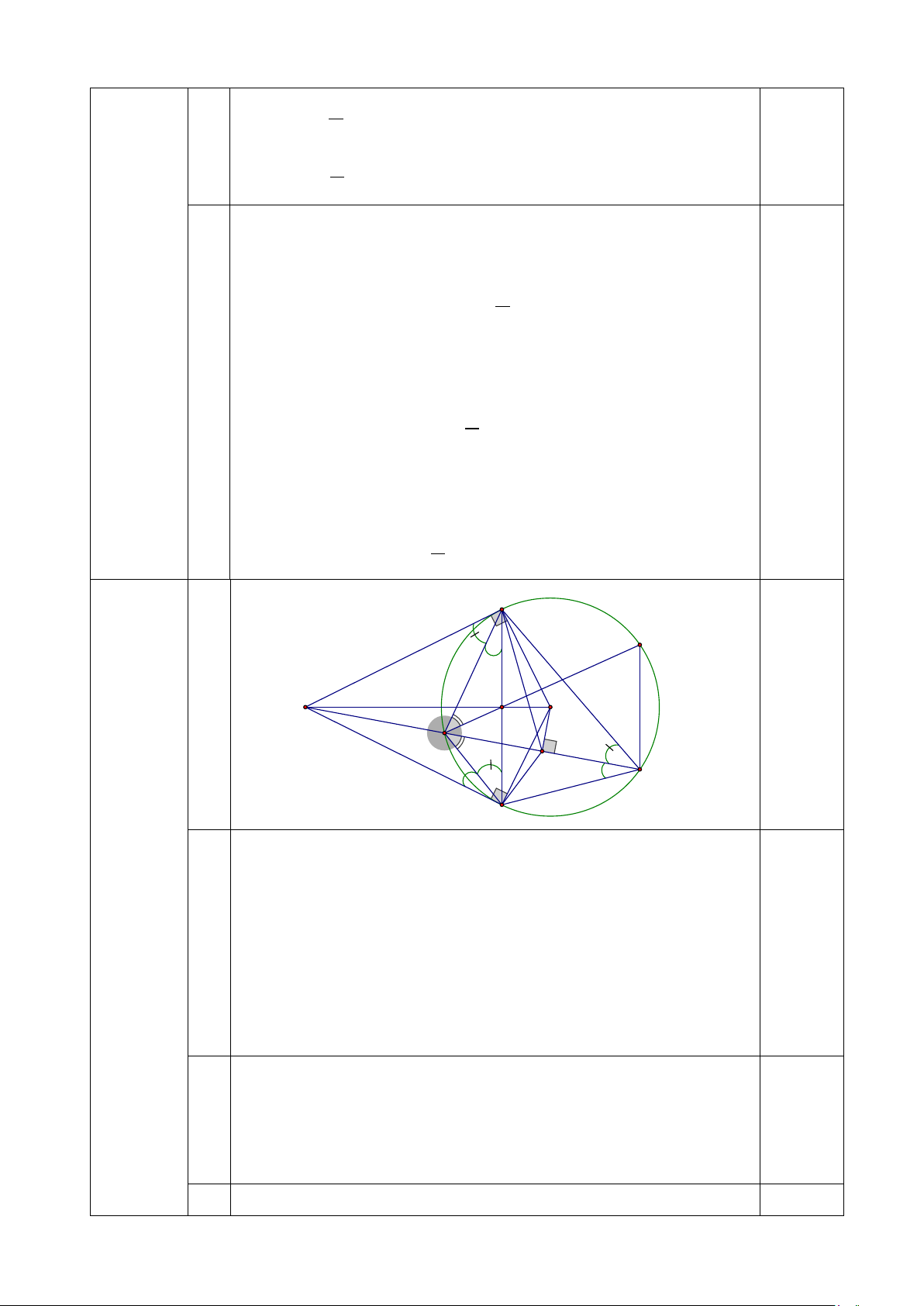
Vậy (x, y) ∈ {(1; 2), ( 1 ; 1)}. 0,25 2 Vẽ hình đúng, khoa học M D H A O 0,5 B I C N - Vì  =  0
AMO ANO = 90 (tính chất tiếp tuyến) ⇒  +  0
AMO ANO =180 ⇒ AMON nội tiếp đường tròn 0,5 6 đường kính AO (1)
(6điểm) a - Vì I là trung điểm của BC ⇒ OI⊥ BC ⇒  0 OIA = 90 ⇒  +  0
AMO AIO =180 ⇒AMOI nội tiếp đường tròn 0,5 đường kính AO (2)
- Từ (1) và (2) ⇒ A, M, O, I, N thuộc đường tròn đường kính AO 0,5
- Vì AMOI nội tiếp ⇒  = 
AIM AOM (cùng chắn cung AM) 0,5 b -  = 
AOM AON(Tính chất 2 tiếp tuyến cắt nhau) 0,5
- Vì AOIN nội tiếp ⇒  = 
AON AIN (cùng chắn cung AN) 0,5 ⇒  = 
AIM AIN hay IA là tia phân giác của  MIN 0,5 c - Vì MN//CD ⇒  =  MBD NBC mà  =  BMH BCN (cùng 0,5 Trang 3/5. chắn 
BN )⇒∆BHM # ∆BNC(g.g) ⇒ HB NB = (3) HM NC - Vì MN/ CD ⇒  =  NBH CBM mà  =  BNH BCM (cùng chắn 
BM ⇒∆BNH #∆BCM(g.g) ⇒ HB MB = (4) 0,5 HN MC - Vì ∆ABN #∆ANC (g.g) NB AB ⇒ = 0,25 NC AN - Vì ∆ABM #∆AMC (g.g) MB AB ⇒ = 0,25 MC AM
mà AM = AN(t/c hai tiếp tiến cắt nhau) ⇒ NB MB = (5) 0,25 NC MC - Từ (3), (4), (5) ⇒ HB HB = ⇒ HM = HN 0,25 HM HN
Áp dụng bất đẳng thức: 1 1 1 9 + + ≥ A B C A + B + C 0,25 (với A, B, C > 0)
Với x, y, z > 0 ta có: 1 1 1 9 + + ≥ xy yz zx xy + yz + zx ⇒ 1 9 Q ≥ + 2 2 2 x + y + z xy + yz + zx 0,25 1 1 1 7 Câu 5 Q ≥ ( + + )+ 2 2 2
x + y + z xy + yz + zx xy + yz + zx xy + yz + zx (2 điểm) 9 7 ≥ + 2 2 2
x + y + z +2xy + 2yz + 2zx xy + yz + zx 0,5 = 9 7 9 21 + ≥ + ≥ 30 2 2 2
(x + y + z) xy + yz + zx (x + y + z) (x + y + z) 0,5
(Do 3(xy + yz + zx) ≤ (x + y + z)2 và x + y + z = 1)
Dấu "=" xẩy ra khi và chỉ khi và 1 x = y = z = 3 0,5 Vậy Qmin = 30⇔ = = = 1 x y z 3
Lưu ý: - Điểm bài thi là tổng điểm của các câu thành phần. Thang điểm toàn bài là
20 điểm, không được làm tròn (điểm lẻ từng ý trong một câu nhỏ nhất là 0,25).
- Thí sinh làm bài bằng cách khác, lập luận chặt chẽ, logic, ra kết quả đúng vẫn cho
điểm tối đa.
-------------Hết------------ Trang 4/5.
Document Outline

• DE 1
• HUONG DAN CHAM DE 1