Đề thi học sinh giỏi Toán 9 năm 2018 – 2019 sở GD&ĐT TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chọn học sinh giỏi môn Toán năm 2018 – 2019 sở GD&ĐT TP HCM giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.
Preview text:
STAR-EDUCATION
16/2 Trần Thiện Chánh, P.12, Q.10
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KÌ THI HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ HỒ CHÍ MINH THÀNH PHỐ Khóa thi ngày 13/3/2019 Môn thi: TOÁN ——————
Thời gian làm bài: 90 phút, không kể thời gian phát đề —————— Bài 1. (4 điểm) 2 1 1 x2 y2
Cho x, y là các số thực sao cho − =
. Tính giá trị của biểu thức + . x y 2x + y y2 x2 Bài 2. (3 điểm)
Cho a, b, c là ba số thực sao cho a + b = c − 2 và ab = 2c2 − 3c + 1. Tìm giá trị lớn nhất
của biểu thức P = a2 + b2 Bài 3. (3 điểm)
An khởi hành từ Sài Gòn đi Biên Hòa. Sau đó 5 phút, Bình và Cường khởi hành từ Biên
Hòa về Sài Gòn. Trên đường đi, An gặp Cường ở địa điểm C rồi gặp Bình ở địa điểm
D. Tính vận tốc của mỗi người, biết rằng quãng đường Sài Gòn - Biên Hòa dài 39 km 3
CD = 6 km; Vận tốc của An bằng 1,5 lần vận tốc của Bình và bằng vận tốc của Cường. 4 Bài 4. (6 điểm)
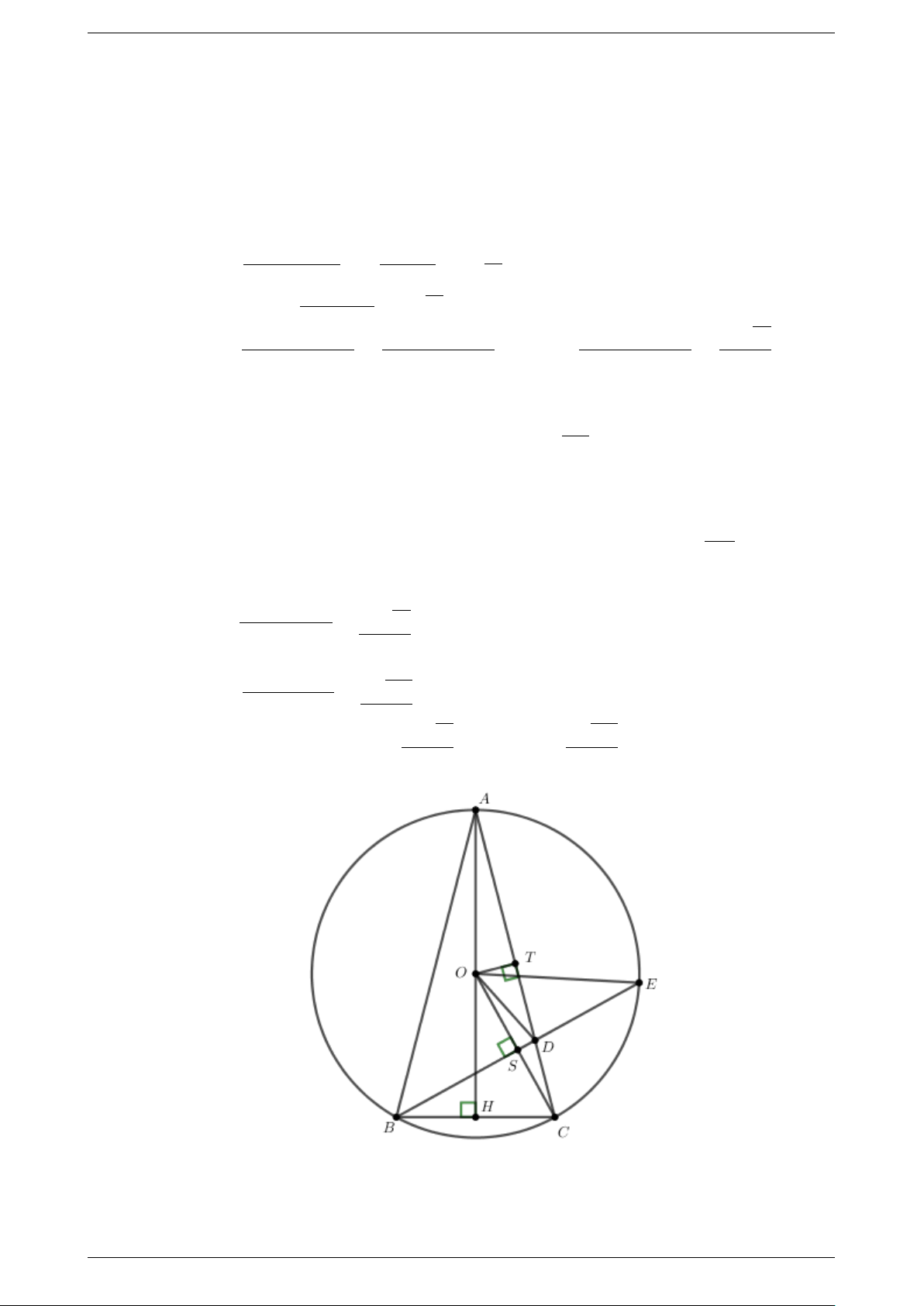
Cho 4ABC cân tại A, nội tiếp đường tròn (O). Từ B kẻ đường thẳng vuông góc với
OC, đường thẳng này cắt AC tại D và cắt (O) tại E (E khác B). Cho biết AB = 8cm
và BC = 4 cm, tính độ dài các đoạn thẳng DE, OA và OD. Bài 5. (4 điểm)
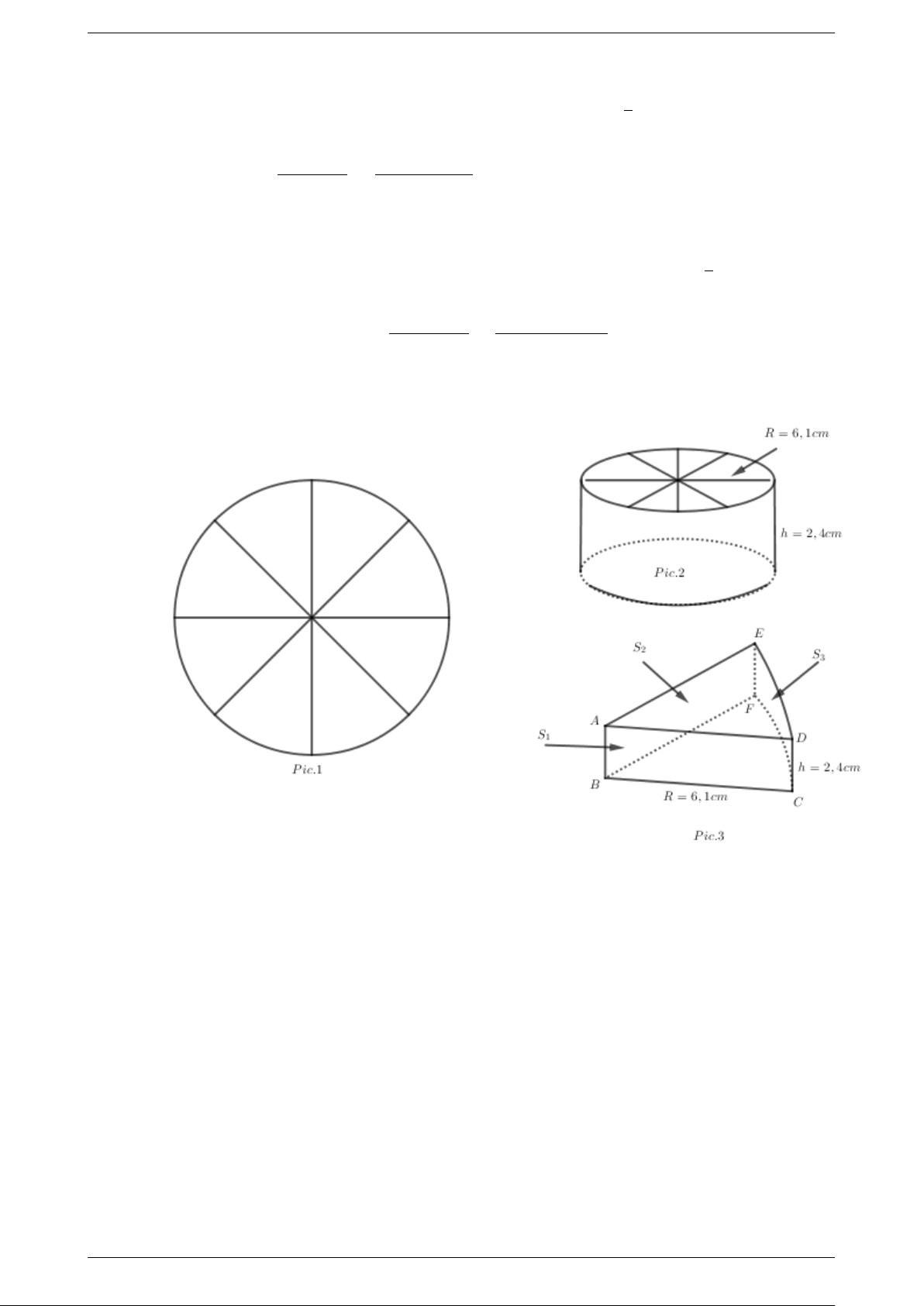
Hộp phô mai có dạng hình trụ, đường kính đáy 12,2 cm và chiều cao 2,4 cm.
a) Biết rằng 8 miếng phô mai được xếp sát bên trong hộp và độ dày của giấy gói từng
miếng không đáng kể. Hỏi thể tích của một miếng phô mai là bao nhiêu?
b) Tính diện tích giấy gói được sử dụng cho một miếng phô mai.
(Ghi kết quả gần đúng chính xác đến 1 chữ số thập phân sau dấu phẩy) – HẾT –
www.star-education.net - Hotline: 0868.733.730 STAR TEAM STAR-EDUCATION
16/2 Trần Thiện Chánh, P.12, Q.10 STAR-EDUCATION
KÌ THI HỌC SINH GIỎI LỚP 9 CẤP THÀNH PHỐ Khóa thi ngày 13/3/2019 Môn thi: TOÁN LỜI GIẢI
Đây là lời giải minh họa môn Toán kì thi học sinh giỏi cấp thành phố của đội ngũ giáo viên
trẻ ở trung tâm “ Star Education”.
Bài 1. Điều kiện: xy 6= 0; y 6= −2x. 2 1 1 2y − x 1 Từ giả thiết: − = ⇔ = ⇔ (2y − x)(2x + y) = xy x y 2x + y xy 2x + y
⇔ 4xy + 2y2 − 2x2 − xy = xy ⇔ 2xy + 2y2 − 2x2 = 0 ⇔ xy + y2 − x2 = 0(∗). y x
Vì xy 6= 0 nên chia phương trình (∗) cho xy, ta được: 1 + − = 0 x y x y x y 2 x2 y2 x2 y2 ⇔ − = 1 ⇔ − = 1 ⇔ + − 2 = 1 ⇔ + = 3 y x y x y2 x2 y2 x2
Bài 2. Ta có: P = a2 + b2 = (a + b)2 − 2ab.
Dùng phương pháp thế, ta được:
P = (c − 2)2 − 2(2c2 − 3c + 1) = c2 − 4c + 4 − 4c2 + 6c − 2 = −3c2 + 2c + 2 2 2 1 1 7 1 2 7 7 = −3 c2 − c − = −3 c2 − 2 · c · + − = −3 c − + ≤ . 3 3 3 9 9 3 3 3 7
Vậy giá trị lớn nhất của P là . 3 −5 1 a + b =
Dấu ” = ” xảy ra ⇔ c = ⇔ 3 3 2 ab = 9 5 2
Hay a, b là nghiệm của phương trình X2 − SX + P = 0 ⇔ X2 + X + = 0 √ √ 3 9 −5 + 17 −5 − 17 a = a = ⇔ 6√ hoặc 6√ −5 − 17 −5 + 17 b = b = 6 6 1 Bài 3. 5 phút = giờ. 12
Gọi vA, vB, vC(vA, vB, vC > 0) lần lượt là vận tốc của An, Bình và Cường. 2vA vB = ⇒ 3 4vA v C = 3
Đặt s(s > 0) là quãng đường mà An đã đi được khi gặp Cường. Kết hợp với CD =
6km ta suy ra quãng đường mà An đã đi được khi gặp Bình là 39 − (s + 6) = 33 − s.
Theo đề, ta có hệ phương trình: s 39 − s 1 − = 4v s 117 − 3s 1 v A 12 A − = 3 vA 4vA 12 s + 6 33 − s 1 ⇔ s + 6 99 − 3s 1 − = − = v 2v 12 v 2v 12 A A A A 3
www.star-education.net - Hotline: 0868.733.730 STAR TEAM STAR-EDUCATION
16/2 Trần Thiện Chánh, P.12, Q.10 12s − 351 + 9s = v 21s − v ⇔ A ⇔ A = 351 12s + 72 − 594 + 18s = vA 30s − vA = 522 v ⇒ v B = 32 A = 48 (t/m) ⇒ vC = 64
Vậy vận tốc của An là 48 km/h; vận tốc của Bình là 32 km/h; vận tốc của Cường là 64 km/h
Bài 4. Gọi AH là đường cao của 4ABC suy ra H là trung điểm của BC.
Theo định lí Pitago vào 4AHB vuông tại H, ta có: √ √ √ AH = AB2 − BH2 = 82 − 22 = 2 15 (cm). AH · BH √ Suy ra SABC = = 4 15 (cm2) 2 √ AB · AC · BC AB · AC · BC AB · AC · BC 16 15 SABC = = ⇒ OA = = (cm). 4R 4 · OA 4 · SABC 15
Gọi S là giao điểm của OC và BE. T là trung điểm của AC ⇒ OT ⊥AC.
Các tứ giác BOSH, OT DS nội tiếp nên: 8
CH · CB = CD · CT (= CS · CO) = 8 ⇒ CD = = 2 (cm) CT
Nên D là trung điểm của CT và AD = 6 cm.
Vậy BC2 = CD · CA(= 16) nên 4ABC v 4BCD(c · g · c) nên 4BCD cũng cân tại B ⇒ BC = BD = 4 (cm). 12
Lại có 4DBC v 4DAE(g · g) ⇒ BD · DE = CD · AD ⇒ DE = = 3(cm). BD
Ta có S là trung điểm của BE nên SE = 3, 5 (cm) ⇒ SD = 0, 5 (cm).
Áp dụng định lí Pitago vào 4OSE vuông tại S, ta có: √ √ 17 15 OS = OE2 − SE2 = (cm). 30
Áp dụng định lí Pitago vào 4OSD vuông tại S, ta có: √ √ 2 285 OD = SD2 + OS2 = (cm). 15 √ √ 16 15 2 285 Vì vậy: DE = 3(cm); OA = (cm); OD = (cm). 15 15
www.star-education.net - Hotline: 0868.733.730 STAR TEAM STAR-EDUCATION
16/2 Trần Thiện Chánh, P.12, Q.10 Bài 5.
a) Bán kính đáy của hình trụ là R = 12, 2 : 2 = 6, 1 (cm). 1
Nhận thấy rằng thể tích của một miếng phô mai bằng
thể tích của cả hộp phô 8 mai.(hình 1 và hình 2). π · R2 · h π · 6, 12 · 2, 4 Nên Vpiece = = ≈ 35, 1(cm3). 8 8
b) Ở hình 3, ta nhận thấy rằng phần diện tích giấy gói một miếng bằng tổng của: 2 lần
diện tích quạt AED(2S2), 2 lần diện tích hình chữ nhật ABCD(2S1) và 1 lần diện 1
tích hình chữ nhật EF DC(S3) là hình chữ nhật có diện tích bằng diện tích xung 8
quanh của cả hộp phô mai. 2 · π · 6, 12 2 · 6, 1 · 2, 4 · π
Nên Spiece = 2 · 2, 4 · 6, 1 + + ≈ 70(cm2). 8 8
www.star-education.net - Hotline: 0868.733.730 STAR TEAM