Đề thi học sinh giỏi Toán 9 năm 2020 – 2021 sở GD&ĐT Ninh Bình

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 9 THCS TỈNH NINH BÌNH NĂM HỌC 2020 - 2021 Môn: TOÁN
ĐỀ THI CHÍ NH THỨC Ngày thi: 09/ 03/2021
Thời gian làm bài: 150 phút (không kể thời gian giao đề)
Đề thi gồm 05 câu, trong 01 trang
Họ và tên thí sinh:................................................................... Số báo danh:......................................
Họ và tên, chữ ký: Giám thị thứ nhất:................................................................................................
Giám thị thứ hai:..................................................................................................
Câu 1 (5,0 điểm) 1. Cho phương trình: 2 2
x − 2(m +1)x + 4m − m = 0 (1) ( x là ẩn, m là tham số).
a) Tìm m để phương trình (1) có hai nghiệm dương phân biệt.
b) Giả sử x , x là hai nghiệm của phương trình (1). Tìm giá trị nhỏ nhất của biểu thức A = x - x . 1 2 1 2  x + 2021− y = 4042
2. Giải hệ phương trình  .  2021− x + y = 4042
Câu 2 (5,0 điểm) 1. Cho đa thức ( ) 2
f x = x + ax + b(a,b∈ ) thỏa mãn f ( ) 1 =1 và f (0) > 3.
a) Chứng minh phương trình f (x) = x có hai nghiệm phân biệt.
b) Tìm số nghiệm của phương trình f (f (x)) = x .
2. Cho hai số thực dương x, y thỏa mãn xy =1. Chứng minh 1 1 2 + + ≥ 3⋅ x y x + y
Câu 3 (7,0 điểm) Cho đường tròn tâm O bán kính R . Dây cung BC cố định, không đi qua tâm O .
Trên tia đối của tia BC lấy điểm A ( A khác B ). Từ A kẻ hai tiếp tuyến AM và AN với đường tròn
(O) (M và N là các tiếp điểm). Gọi I,H lần lượt là trung điểm của BC và MN, BC cắt MN tại K .
1. Chứng minh bốn điểm O,M, N,I cùng thuộc một đường tròn và HK là tia phân giác của  BHC .
2. Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở E . Chứng minh M, N,E thẳng hàng.
3. Đường thẳng ∆ qua điểm M và vuông góc với đường thẳng ON, cắt đường tròn (O) tại điểm
thứ hai là P . Xác định vị trí của điểm A trên tia đối của tia BC để tứ giác AMPN là hình bình hành.
Câu 4 (3,0 điểm)
1. Tìm các số nguyên x, y thoả mãn: 2 y x − 5x + 7 = 3 .
2. Cho một bảng ô vuông m× n (gồm m dòng và n cột). Cho
quy tắc tô màu bảng ô vuông như sau: Mỗi ô vuông đơn vị được tô
bằng màu đỏ hoặc màu xanh sao cho bất kì bảng ô vuông 2×3 hoặc
3× 2 nào cũng có đúng hai ô được tô màu đỏ.
a) Hãy chỉ ra một cách tô màu theo quy tắc trên cho bảng ô vuông 4×6 (Điền chữ Đ vào ô được
tô màu đỏ, chữ X vào ô được tô màu xanh).
b) Người ta đã tô bảng ô vuông 2021× 2022 theo quy tắc trên. Hỏi bảng ô vuông này có bao nhiêu ô được tô màu đỏ?
-------------Hết------------
SỞ GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM TỈNH NINH BÌNH
ĐỀ THI CHỌN HSG LỚP 9 THCS CẤP TỈNH NĂM HỌC 2020 - 2021
Môn: Toán - Ngày thi 09/3/2021
(Hướng dẫn chấm này gồm 07 trang)
I. Hướng dẫn chung
1. Bài làm của học sinh đúng đến đâu cho điểm đến đó.
2. Học sinh có thể sử dụng kết quả câu trước làm câu sau.
3. Đối với bài hình, nếu vẽ sai hình hoặc không vẽ hình thì không cho điểm những phần có
liên quan đến hình sai hoặc thiếu đó.
4. Nếu thí sinh làm bài không theo cách nêu trong đáp án mà đúng vẫn cho điểm đủ từng
phần như hướng dẫn, thang điểm chi tiết do tổ chấm thống nhất.
5. Việc chi tiết hoá thang điểm (nếu có) so với thang điểm trong hướng dẫn phải đảm bảo
không sai lệch và đảm bảo thống nhất thực hiện trong toàn hội đồng chấm.
6. Điểm toàn bài thi lẻ đến 0.25.
II. Hướng dẫn chi tiết Câu Đáp án Điểm
1. ( 3 điểm) Cho phương trình: 2 2
x − 2(m +1)x + 4m − m = 0 (1) ( x là ẩn, m là tham số).
a) Tìm m để phương trình (1) có hai nghiệm dương phân biệt.
b) Giả sử x , x là hai nghiệm của phương trình (1). Tìm giá trị nhỏ nhất của biểu thức 1 2 A = x - x . 1 2 a) ( 1.5 điểm) Ta có: 2 2 2
Δ'=(m +1) − (4m − m )=2m − 2m +1. 0.25 2  1  1 =2 m − + >  0 , m ∀ ∈    2  2 0.25
Nên phương trình luôn có hai nghiệm phân biệt với m ∀ ∈  . S  > 0 2(m +1) > 0
Do đó phương trình có hai nghiệm dương phân biệt ⇔  ⇔  0.5 P > 0 2 4m − m > 0 Câu 1 (5.0 m > 1 − ⇔  ⇒ < < điểm) 0 m 4. 0.5 0 < m < 4 b) ( 1.5 điểm)
Theo chứng minh trên phương trình đã cho luôn có hai nghiệm phân biệt x ,x với 1 2 x + x =2(m +1) m ∀ ∈  và 1 2  . 2 x x =4m −  m 1 2 Ta có: 2 2
A = x − x = (x − x ) = (x + x ) − 4x x 0.5 1 2 1 2 1 2 1 2 2 2 = 4(m +1) − 4(4m − m ) 2 = 8m −8m + 4 0.5 2 = 2(2m −1) + 2 ≥ 2
Dấu bằng xảy ra khi và chỉ khi 1 m = . 2 0.5
Vậy giá trị nhỏ nhất của biểu thức A bằng 2 khi 1 m = . 2 2  x + 2021− y = 4042
2. (2.0 điểm) Giải hệ phương trình  .  2021− x + y = 4042  ≤ ≤ Điều kiện 0 x 2021  0.25 0 ≤ y ≤ 2021
Cách 1. Áp dụng bất đẳng thức Cauchy-Schwarz có = ( + − )2 4042 x
2021 y ≤ 2(x + 2021− y) 0.5 ⇒ x − y ≥ 0 (1)
Đẳng thức xảy ra khi và chỉ khi x = 2021− y ⇔ x = 2021− y . 0.25
Áp dụng bất đẳng thức Cauchy-Schwarz có = ( + − )2 4042 y 2021 x ≤ 2(y + 2021− x) 0.25 ⇒ x − y ≤ 0 (2)
Đẳng thức xảy ra khi và chỉ khi y = 2021− x ⇔ y = 2021− x 0.25
Từ (1) và (2) suy ra x = y . Từ đó suy ra 2021 x = y =
(thỏa mãn điều kiện). 0.25 2
Hệ phương trình đã cho có một nghiệm  2021 2021 (x;y)  ;  = . 0.25 2 2   
Cách 2. Từ 2 phương trình của hệ ta có: x + 2021− y = 2021− x + y 0.5 (*)
⇔ x − 2021− x = y − 2021− y 0.25
Câu 1 Xét phương trình (*) : (5.0
• Nếu x > y thì − 2021− x > − 2021− y ⇒ VT > VP ( mâu thuẫn ). 0.25 điểm)
• Nếu x < y ⇒ VT < VP ( mâu thuẫn ). 0.25
• Nếu x = y . Hệ phương trình đã cho trở thành x = y x = y   ⇔   x + 2021− x = 4042 2 x (2021− x) = 2021   2021 0.25 x x y = =    2 ⇔  ⇔ 
(thỏa mãn điều kiện). (  2x −  )2 2021 = 0 2021 y =  2  
Hệ phương trình đã cho có một nghiệm 2021 2021 (x;y) =  ; . 0.25 2 2   
Cách 3. Từ 2 phương trình của hệ ta có: x + 2021− y = 2021− x + y 0.5
⇔ ( x − y) + ( 2021− y − 2021− x ) = 0 0.25 x − y ⇔ ( x − y) + = 0 2021− y + 2021− x
( vì (x;y) = (2021;2021) không phải là nghiệm của hệ phương trình đã cho nên nếu hệ
phương trình có nghiệm (x;y) thì 2021− y + 2021− x ≠ 0 ) 0.5  +  x y ⇔ ( x − y)1+  = 0  2021 y 2021 x  − + −   3 x + y ⇔ = > x y ( vì 1+ 0 ) 0.25 2021− y + 2021− x
Hệ phương trình đã cho trở thành x = y x = y   ⇔   x + 2021− x = 4042 2 x (2021− x) = 2021   2021 0.25 x x y = =    2 ⇔ ( ⇔ 
(thỏa mãn điều kiện).  2x −  )2 2021 = 0 2021 y =  2
Hệ phương trình đã cho có một nghiệm  2021 2021 (x;y) ;  =  . 0.25 2 2    Câu 2
1. ( 3.0 điểm) Cho đa thức ( ) 2
f x = x + ax + b(a,b∈ ) thỏa mãn f ( ) 1 =1 và f (0) > 3.
a) Chứng minh phương trình f (x) = x có hai nghiệm phân biệt.
b) Tìm số nghiệm của phương trình f (f (x)) = x . a) 2.0 điểm f ( ) 1 =1 1  + a + b =1 a = −b Vì ( ) 2 f x =x +ax+b nên ta có  ⇔  ⇔ 0.5  f  (0) > 3 b > 3 b > 3 ( ) 2 2
f x = x ⇔ x + ax + b = x ⇔ x − (b +1)x + b = 0 (*) 0.5
Ta có 1+[−(b +1)]+ b = 0 nên phương trình (*) có hai nghiệm x =1;x =b 1 2 Mà b > 3 nên x ≠ x 2 1 0.5 =
Do đó phương trình f (x) x có hai nghiệm phân biệt. 0.5 b) 1.0 điểm Câu 2 (5.0 ( ( )) 2 = ⇔ ( )+ ( ) 2 f f x x
f x af x + b = x ⇔ f (x) − bf (x) + b − x = 0 0.25 điểm) 2 ⇔ ( ) 2 − − ( ) 2 f x x
bf x + bx + x − bx + b − x = 0 ⇔ f  (x) − x f
  (x) + x − b +1 = 0  ⇔ f  (x) 2
− x x − bx + b + x − b +1 = 0    0.25 2 ⇔ f  (x) − x x −  (b − )1x +1 = 0   f (x) − x = 0 ⇔  2 x −  (b − )1x +1= 0
Phương trình f (x) = x (1) có hai nghiệm phân biệt là 1 và b. Xét phương trình 2 x − (b − )
1 x +1=0 (2) có ∆ = ( − )2 b 1 − 4=(b + )
1 (b − 3) > 0 (vì b>3) 0.25
Nên phương trình (2) có hai nghiệm phân biệt.
Ta lại có x =1; x = b không là nghiệm của phương trình (2)
Vậy phương trình f (f (x)) = x có 4 nghiệm phân biệt. 0.25 4 2. ( 2.0 điểm)
Cho hai số thực dương x, y thỏa mãn xy =1. Chứng minh 1 1 2 + + ≥ 3⋅ x y x + y x + y x + y 2 Ta có: 1 1 2 xy xy 2 2 + + = + + = x + y + = + ( + ) 0.5 x y x + y x y x + y x + y 2 2 x + y Câu 2 + +
Áp dụng bất đẳng thức AM-GM ta có: x y x y ≥ xy ⇔ ≥ 1 (1) ( vì xy =1) 0.5 (5.0 2 2
điểm) Tương tự áp dụng bất đẳng thức AM-GM ta có: x + y 2 x + y 2 x + y 2 + ≥ 2 ⋅ ⇔ + ≥ 2 (2) 0.5 2 x + y 2 x + y 2 x + y Từ (1) và (2) suy ra: 1 1 2 + +
≥ 3⋅ Đẳng thức xảy ra khi x = y =1 x y x + y 0.5
Câu 3 (7.0 điểm) Cho đường tròn tâm O bán kính R . Dây cung BC cố định, không đi qua
tâm O . Trên tia đối của tia BC lấy điểm A ( A khác B ). Từ A kẻ hai tiếp tuyến AM và
AN với (O) ( M và N là các tiếp điểm). Gọi I,H lần lượt là trung điểm của BC và MN , BC cắt MN tại K .
1. Chứng minh 4 điểm O,M, N,I cùng thuộc 1 đường tròn và HK là tia phân giác của  BHC .
2. Hai tiếp tuyến của (O) tại B và C cắt nhau ở E . Chứng minh M, N,E thẳng hàng.
3. Đường thẳng ∆ qua điểm M và vuông góc với đường thẳng ON, cắt đường tròn (O) tại
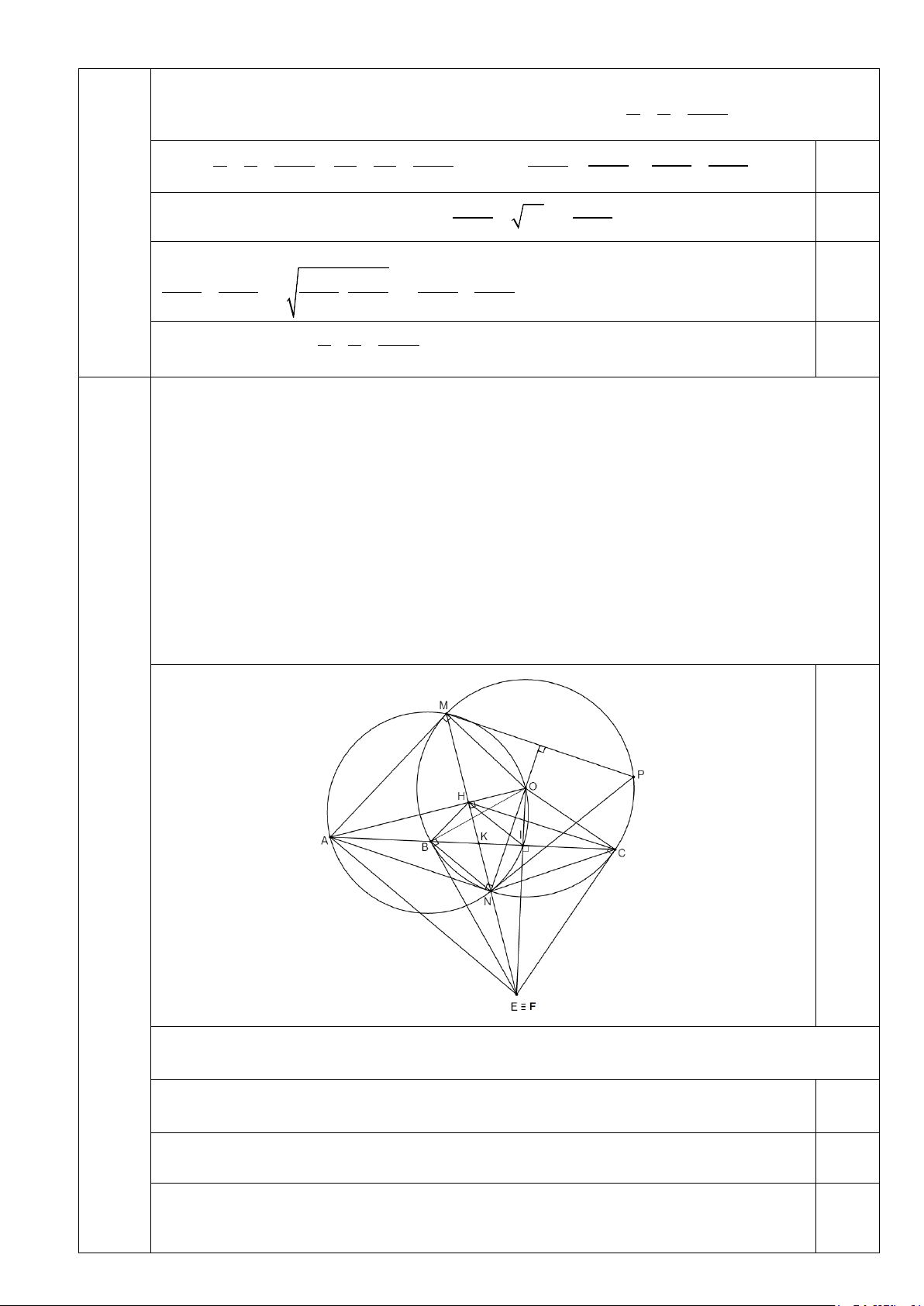
điểm thứ hai là P . Xác định vị trí của điểm A trên tia đối của tia BC để tứ giác AMPN là hình bình hành. Câu 3 (7.0 điểm)
1.( 3.0 điểm)
Chứng minh 4 điểm O,M, N,I cùng thuộc 1 đường tròn và HK là tia phân giác của  BHC .
*) Ta có: AM ⊥ OM ( tính chất tiếp tuyến) ⇒ AM ∆ O vuông tại M
⇒ Ba điểm A,M,O cùng thuộc đường tròn đường kính AO (1) 0.5
Chứng minh tương tự suy ra: ba điểm A,N,O cùng thuộc đường tròn đường kính AO (2) 0.5
Mặt khác ta có: I là trung điểm của BC (giả thiết)
⇒ OI ⊥ BC ( Quan hệ vuông góc giữa đường kính và dây cung) ⇒ A
∆ IO vuông tại I ⇒ Ba điểm A,I,O cùng thuộc đường tròn đường kính AO (3) 0.5 5
Từ (1), (2) và (3) suy ra: 4 điểm O,M, N,I cùng thuộc 1 đường tròn. 0.5
*) Ta có: OM = ON(= R) ⇒ O∈ đường trung trực của MN (4)
AM = AN ( tính chất hai tiếp tuyến cắt nhau) ⇒ A ∈ đường trung trực của MN (5)
HM = HN(gt) ⇒ H ∈ đường trung trực của MN (6)
Từ (4), (5) và (6) suy ra O,H,A thẳng hàng và OA là đường trung trực của MN 0.25 Xét AN ∆
O vuông tại N có NH ⊥ AO ( OA là đường trung trực của MN ) 2
⇒ AN = AH ⋅AO ( Hệ thức lượng trong tam giác vuông) (*)
Chứng minh ΔABN∽ΔANC(g.g) AB AN 2 ⇒ = ⇒ AN = AB⋅AC (**) AN AC Từ (*) và (**) suy ra: AB AO AB⋅AC = AH ⋅AO ⇒ = 0.25 AH AC
ΔABH∽ΔAOC( .cg.c) ⇒  =  AHB ACO (7)
⇒ Tứ giác BHOC nội tiếp ⇒  =  CHO CBO 0.25 Mà:  =  BCO CBO ( O
∆ BC cân tại O ) Nên ⇒  =  CHO BCO (8)
Từ (7) và (8) suy ra: ⇒  =  ⇒  =  AHB CHO
KHB CHK ( phụ với hai góc bằng nhau) 0.25
⇒ HK là tia phân giác của góc  BHC . 2. ( 2.0 điểm)
Hai tiếp tuyến của đường tròn (O) tại B và C cắt nhau ở E . Chứng minh M, N,E thẳng hàng
Câu 3 Cách 1. Chỉ ra O,I,E thẳng hàng 0.25 (7.0 2 điểm) ON = OH⋅OA Ta có 
( Hệ thức lượng trong tam giác vuông) 0.5 2 OB = OI⋅OE ⇒ OH ⋅OA = OI⋅OE 0.25
Suy ra tứ giác AHIE nội tiếp. 0.25 Suy ra  = 
AHE AIE = 90 ⇒ HE ⊥ AO tại H . 0.25
Lại có MN vuông góc với AO tại H 0.25 Nên M,N,E thẳng hàng. 0.25
Cách 2. Gọi F là giao điểm của MN với OI . Chỉ ra ΔAIO∽ΔFHO(g.g) 0.5 OI OA ⇒ =
⇒ OI⋅OF = OA ⋅OH 0.25 OH OF Mà: 2 2 OH ⋅OA = ON = OC 0.25 Nên: 2
OI.OF = OC ⇒ ΔOCF∽ΔOIC( .cg.c) 0.5 ⇒  = 
FCO CIO = 90 ⇒ FC ⊥ OC tại C .Suy ra FC là tiếp tuyến của đường tròn (O) 0.25
Chứng minh tương tự FB là tiếp tuyến của đường tròn (O)
Do đó F là giao điểm hai tiếp tuyến của đường tròn (O) tại B và C . 0.25
Vậy E ≡ F , ta có điều phải chứng minh. 3.(2.0 điểm)
Đường thẳng ∆ qua điểm M và vuông góc với đường thẳng ON, cắt đường tròn (O) tại
điểm thứ hai là P . Xác định vị trí của điểm A trên tia đối của tia BC để tứ giác AMPN là hình bình hành. MO ⊥ NP
Cách 1: Tứ giác AMPN là hình bình hành thì suy ra  . 0.25 NO ⊥ MP
Suy ra O vừa là trực tâm vừa là tâm đường tròn ngoại tiếp tam giác MNP 0.25 ⇒ M
∆ NP là tam giác đều. 0.25 6
Do bán kính đường tròn ngoại tiếp tam giác MNP bằng R nên MP = R 3 = AN 0.25
Xét tam giác vuông ANO ta có 2 2 AO = AN + NO = 2R . 0.25
⇒ A là giao điểm của đường tròn (O;2R) với tia đối của tia BC. 0.25
Khi A là giao điểm của đường tròn (O;2R) với tia đối của tia BC, chứng minh tứ 0.25
giác AMPN là hình bình hành.
Vậy A là giao điểm của đường tròn (O;2R) với tia đối của tia BC thì tứ giác 0.25 AMPN là hình bình hành.
Câu 3 Cách 2: Tứ giác AMPN là hình bình hành ⇒ APđi qua trung điểm H của MN (7.0
⇒ Tứ giác AMPN là hình thoi (hình bình hành có hai đường chéo vuông góc) 0.5 điểm)
⇒ A,H,O,P thẳng hàng và  =  MAP MPA 0.25 Xét (O;R) có   MOA MPA =
( hệ quả góc nội tiếp) 0.25 2 ⇒   MOA =  0 MAO MAO 30 ⇒ = ( AM ∆ O vuông tại M ) 0.25 2 AO ⇒ MO =
( cạnh đối diện với góc 0
30 trong tam giác vuông) ⇒ OA = 2R 0.25 2
Khi A là giao điểm của đường tròn (O;2R) với tia đối của tia BC, ta chứng minh 0.25
được tứ giác AMPN là hình bình hành.
Vậy A là giao điểm của đường tròn (O;2R) với tia đối của tia BC thì tứ giác
AMPN là hình bình hành. 0.25 Câu 4 − + =
1. (1.0 điểm) Tìm các số nguyên x, y thoả mãn: 2 y x 5x 7 3 (*) + Nếu y ≤ 0 ta có: 2 2
x − 5x + 7 ≤1 ⇔ x − 5x + 6 ≤ 0 ⇔ 2 ≤ x ≤ 3
Do x nguyên nên ta có x ∈{2; } 3 . 0.25
Lần lượt thay giá trị của x vào phương trình (*) tìm được (x,y)∈{(2;0);(3; } 0) x =1
+ Nếu y =1 thì phương trình (*) trở thành: 2 2
x − 5x + 7 = 3 ⇔ x − 5x + 4 = 0 ⇔  x = 4 0.25 ⇒ (x,y)∈{(1;1);(4; }
1) thỏa mãn phương trình (*) + Nếu y ≥ 2 thì y 3 9
Cách 1. Ta xét VT (*) theo các trường hợp số dư của x khi chia cho 3
Câu 4 - Nếu x = 3k (k∈) thì 2 2
x − 5x + 7 = 9k −15k + 7 không chia hết cho 3 (3.0
điểm) nên phương trình (*) vô nghiệm
- Nếu x = 3k +1 (k ∈) thì 2 2 2
x − 5x + 7 = (3k +1) − 5(3k +1) + 7 = 9k − 9k + 3 không
chia hết cho 9 nên phương trình (*) vô nghiệm
- Nếu x = 3k + 2 (k ∈) thì 2 2 2
x − 5x + 7 = (3k + 2) − 5(3k + 2) + 7 = 9k − 3k +1 không 0.25
chia hết cho 3 nên phương trình (*) vô nghiệm.
Cách 2. Ta có 2 y 2 y
x − 5x + 7 = 3 ⇔ x − 5x + 7 − 3 = 0 (1)
Coi phương trình (1) là phương trình bậc hai ẩn x, tham số y có: y y y 1 −
∆ = 25 − 4(7 − 3 ) = 4.3 − 3 = 3(4 ⋅3 −1) Vì y 1
4⋅3 − −1/3 nên ∆ không phải là số chính phương.
Với y nguyên, y ≥ 2 phương trình (1) là phương trình bậc hai có hệ số nguyên mà ∆
không phải là số chính phương nên phương trình (1) không có nghiệm nguyên.
Vậy (x, y)∈{(2;0);(3;0);(1;1);(4;1 } ) 0.25 7
2. ( 2.0 điểm) Cho một bảng ô vuông m× n (gồm m dòng và n cột). Cho quy tắc tô màu bảng
ô vuông như sau: Mỗi ô vuông đơn vị được tô bằng màu đỏ hoặc màu xanh sao cho bất kì bảng
ô vuông 2×3 hoặc 3× 2 nào cũng có đúng hai ô được tô màu đỏ.
a) Hãy chỉ ra một cách tô màu theo quy tắc trên cho bảng ô vuông 4×6 (Điền chữ Đ vào ô
được tô màu đỏ, chữ X vào ô được tô màu xanh).
b) Người ta đã tô bảng ô vuông 2021× 2022 theo quy tắc trên. Hỏi bảng ô vuông này có bao
nhiêu ô được tô màu đỏ?
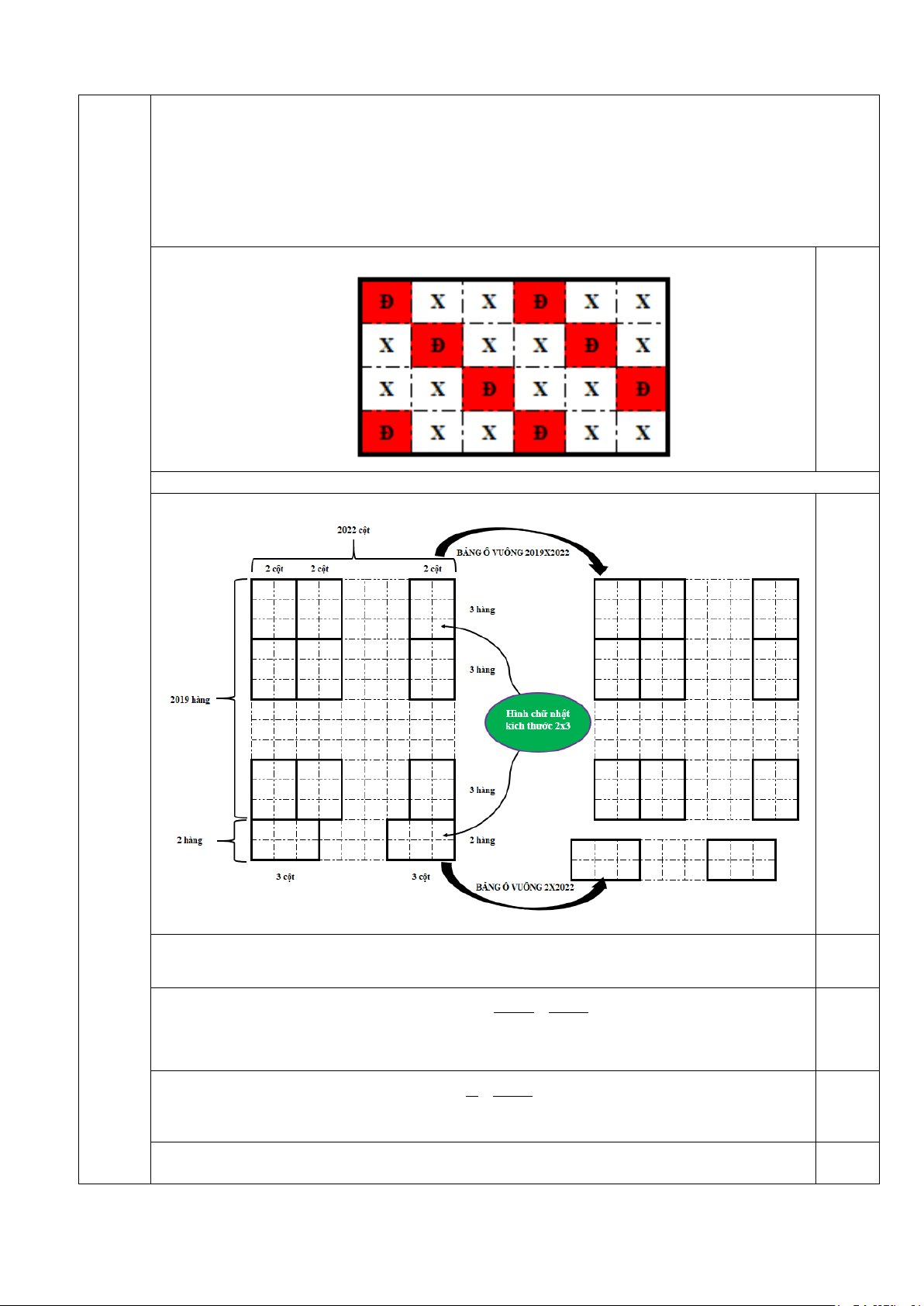
a) 1.0 điểm: Chỉ ra 1 cách tô đúng Ví dụ 1.0 b) 1.0 điểm Câu 4 (3.0 điểm)
Chia bảng ô vuông ban đầu thành hai bảng ô vuông 2019× 2022 và 2× 2022 ( xem hình vẽ minh họa) 0.25
Bảng ô vuông 2019× 2022 được chia thành 2022 2019 × = 680403 bảng ô vuông 2 3 0.25
3× 2. Trong bảng ô vuông 2019× 2022 có 680403⋅2 =1360806 ô được tô màu đỏ.
Bảng ô vuông 2× 2022 được chia thành 2 2022 ×
= 674 bảng ô vuông 2×3. Trong 2 3 0.25
bảng ô vuông 2× 2022 có 674⋅2 =1348 ô được tô màu đỏ.
Bảng ô vuông ban đầu có: 1360806 +1348 =1362154 ô được tô màu đỏ. 0.25
-----------Hết---------
Document Outline

• TOAN-HSG9-2021
• HDC TOAN-HSG 9-2021