Đề thi học sinh giỏi Toán 9 năm 2022 – 2023 phòng GD&ĐT thành phố Thái Nguyên

UBND THÀNH PHỐ THÁI NGUYÊN
THI CHỌN HỌC SINH GIỎI LỚP 9
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2022 – 2023
MÔN THI : TOÁN ĐÁP ÁN
(Thời gian 150 phút không kể thời gian giao đề)
(Đề thi gồm có 01 trang) 3 3 3 3 2 7 2 10 3 4 3 2 1
Bài 1 (3 điểm). Rút gọn biểu thức A + + + − − = 5 + 2 +1 Lời giải: 3 3 3 3
2 + 7 + 2 10 + 3 4 − 3 2 −1 A = 5 + 2 +1 3 2 + ( 2 + 5)2 3 3 3 2 3 3 + 1− 3 2 + 3 2 − 2 = 5 + 2 +1 3 2 + ( 2 + 5)2 3 3 3 + (1− 2) = 5 + 2 +1 3 3 2 + 2 + 5 +1− 2 2 + 5 +1 = = = 1 5 + 2 +1 5 + 2 +1 Vậy A=1  x + 2 x 1  x −1
Bài 2 (6 điểm). Cho biểu thức B =  + +  : .
x x −1 x + x +1 1−  x 2 
a. Rút gọn biểu thức B. 2
b. Tìm giá trị của x để B = . 7
c. Tìm giá trị nguyên của x để giá trị của biểu thức B là số nguyên. d. So sánh 2 B và 2B . Lời giải: a.  x + 2 x 1  x −1 B =  + +  :
x x −1 x + x +1 1−  x 2   (x + 2) x( x −1) (x + x +1)  x −1 =  + −  :
( x −1)(x + x +1) ( x −1)(x + x +1) ( x −1)(x + x +  1) 2  2 x − 2 x +1 2 2( x −1) 2 = . = = 2
( x −1)(x + x +1) x −1 ( x −1) (x + x +1) x + x +1 2 Vậy B =
Với x ≥ 0; x ≠1. x + x +1 b. Ta có 2 2 2 B = ⇔
= ⇔ x + x +1= 7 7 x + x +1 7
⇔ x + x − 6 = 0 ⇔ ( x + 3)( x − 2) = 0   x + 3 = 0  x = 3( − loai) ⇔  ⇔   x − 2 = 0  x = 2 ⇔ x = 4( dkxd tm )
c. Do x ≥ 0; x ≠1 nên x + x +1≥1 x ∀ 2 2 Do đó 0 ≤
≤ = 2 mà B∈ Z ⇒ B∈{1; } 2 x + x +1 1 2 +) Nếu B =1⇔
=1⇔ x + x +1= 2 x + x +1 2  1  5
⇔ x + x −1= 0 ⇔ x + = 1  mà ( x + > 0) 2    4 2 1 5 5 −1 3 − 2 5 ⇔ x + = ⇔ x = ⇔ x = (tm). 2 2 2 2 2 +) Nếu B = 2 ⇔
= 2 ⇔ x + x +1=1 x + x +1
⇔ x + x = 0 ⇔ x ( x + )
1 = 0 mà ( x +1> 0)
⇔ x = 0 ⇔ x = 0(tm).  3 − 2 5  Vậy để B Z x 0;  ∈ ⇔ ∈ .  2   2 2( − x + x)
d. Xét hiệu B − 2 = − 2 = < 0 x + x +1 x + x +1
Vì x ≥ 0; x ≠1⇒ x + x > 0 và x + x +1> 0 Ta có 2
B − 2B = B(B − 2) < 0 do B > 0 Vậy 2 B < 2B . Bài 3 (3 điểm).
a. Trong mặt phẳng toạ độ Oxy, cho đường thẳng (d) : y = (m − 2)x + 3 (m ≠ 3). Tìm
tất cả các giá trị của tham số m để đường thẳng (d) cắt Ox tại điểm A, cắt Oy tại điểm B sao cho  = o ABO 30 . 2 2  x + 4y = 5
b. Giải hệ phương trình:  2 2
4x y + 8xy + 5x +10y =1 Lời giải:
a. Cho x = 0; y = 3 ta được B(0;3)∈Oy 3 − Cho y = 0; x = ta được m − 2 3 ( − A ;0)∈Ox m − 2 3 − Suy ra, ta có: OA = ; OB = 3 m − 2 Ta có:  OA 3 − 0 3 tanOBA = ⇒ :3 = tan30 = OB m − 2 3  m = 3 + 2 ⇒ m − 2 = 3 ⇒  m = − 3 + 2 2 2  x + 4y = 5 b.  2 2
4x y + 8xy + 5x +10y = 1 2
(x + 2y) − (4xy + 5) = 0 ⇔ 
 (x + 2y)(4xy + 5) = 1
 x + 2y = a Đặt  4xy + 5 = b 2 a − b = 0 a = 1
Ta có hệ phương trình  ⇔   ab = 1 b = 1  x + 2y = 1  x =1− 2y  x =1− 2y Ta có  ⇔  ⇔  2 4xy + 5 = 1
4y(1− 2y) + 5 = 1  8
− y + 4y + 4 = 0  x = 1; − y =1   1 − x = 2; y =  2 1 − Vậy ( ; x y)thoả mãn là ( 1 − ;1); (2; ) 2
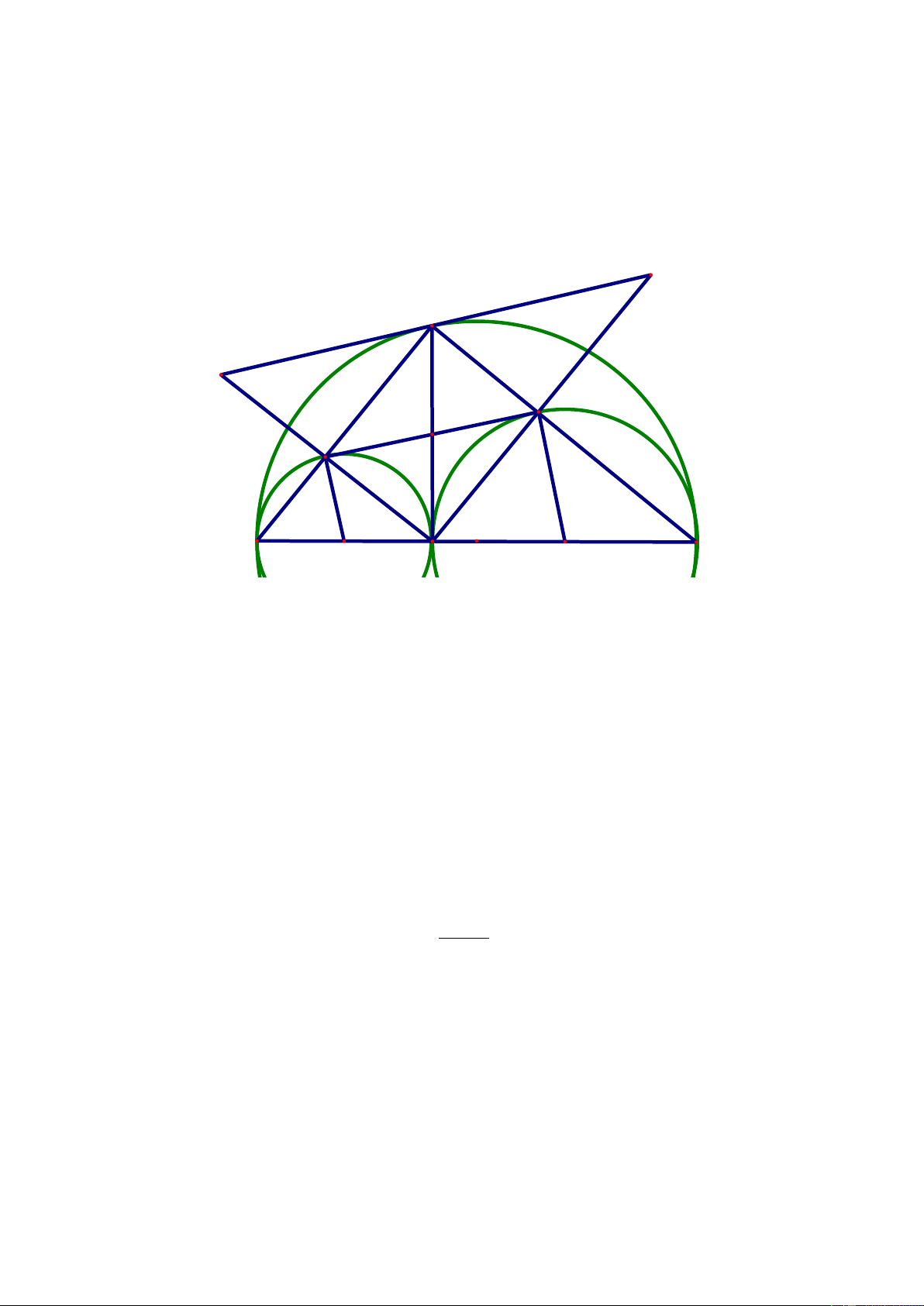
Bài 4 (6 điểm). Cho nửa đường tròn tâm O , đường kính AB , điểm M di động trên nửa
đường tròn đó (M ≠ ,
A M ≠ B) . Gọi điểm H là hình chiếu vuông góc với điểm M trên
đường thẳng AB. Vẽ đường tròn đường kính AH, đường tròn đường kính BH. Đường thẳng
MA cắt đường tròn đường kính AH tại điểm E (E ≠ )
A . Đường thẳng MB cắt đường tròn
đường kính BH tại điểm F (F ≠ B) .
e. Chứng minh: ME.MA = MF.MB .
f. Gọi K, G lần lượt là hai điểm đối xứng của điểm H qua các đường thẳng ,
MA MB . Chứng minh rằng ba điểm M, K, G thẳng hàng. g. Chứng minh : 3 MH = A . B AE.BF
h. Gọi I, J lần lượt là tâm của đường tròn đường kính AH và BH. Cho AB = 2R .
Xác định vị trí của điểm M để diện tích tứ giác IEFJ đạt giá trị lớn nhất. Tính giá trị đó theo R. Lời giải G M K F E D A I H O B J
a) Xét ∆AHM vuông tại H có HE ⊥ AM (Vì 
AEH là góc nội tiếp chắn nửa đường tròn đường kính AH nên  o
AEH = 90 ), áp dụng hệ thức về cạnh góc vuông và hình chiếu của nó
trên cạnh huyền ta có: MH2 = ME.MA
Xét ∆BHM vuông tại H có HF ⊥ BM (Vì 
BFH là góc nội tiếp chắn nửa đường tròn đường kính BH nên  o
BFH = 90 ), áp dụng hệ thức về cạnh góc vuông và hình chiếu của nó trên
cạnh huyền ta có: MH2 = MF.MB
⇒ ME.MA = MF.MB (Vì cùng bằng MH2)
b) Có K đối xứng với H qua AM ⇒ AM là đường trung trực của KH
⇒ KM = KH, MA ⊥ KH tại E ⇒ ∆MKH cân tại M, có ME là đường cao nên cũng là đường KMH phân giác của       KMH ⇒ KME = EMH = ⇒ KMH = 2.EMH 2 CMTT ta có MG = MH,   GMH = 2.FMH
Xét đường tròn (O) đường kính AB, có 
AMB là góc nội tiếp chắn nửa đường tròn nên  o AMB = 90 ⇒        o o
KMH + GMH = 2.EMH + 2.FMH = 2(EMH + FMH) = 2.AMB = 2.90 = 180 ⇒ K, M, G thẳng hàng.
c) Áp dụng một số hệ thức về cạnh và đường cao trong tam giác vuông ta có:
AM.BM = MH.AB; AH2 = AE.AM; BH2 = BF.BM; MH2 = AH.HB
⇒ MH4 = AH2.HB2 = (AE.AM). (BF.BM) = (AM.BM).AE.BF = MH.AB.AE.BF ⇒ MH3 = AB.AE.F
d) Tứ giác MEHF có    o
M = E = F = 90 nên là hình chữ nhật. Gọi D là giao điểm của MH và
EF ⇒ EF = MH; DE = DH (Tính chất đường chéo hình chữ nhật)
Xét ∆DEI và ∆DHI, có: EI = HI, DI chung, DE = DH ⇒ ∆DEI = ∆DHI   o ⇒ DEI = DHI = 90 CMTT ta có:   o DFJ = DHJ = 90 ⇒   o
IEF = JFE = 90 ⇒ Tứ giác IEFJ là hình thang vuông (EI + FJ).EF
⇒ Diện tích tứ giác IEFJ: S = IEFJ 2 AH HB ( + ).EF Mà 1 1 EI AB.EF 2R.MH R.MH = ⋅ AH;FJ = ⋅ HB⇒ 2 2 S = = = = 2 2 IEFJ 2 4 4 2
Diện tích tứ giác IEFJ lớn nhất khi và chỉ khi MH lớn nhất ⇔ M nằm chính giữa cung AB. 2 Khi đó MH = R R.MH R ⇒ S = = IEFJ 2 2 2
Vậy diện tích tứ giác IEFJ lớn nhất bằng R khi M nằm chính giữa cung AB. 2 Bài 5 (2 điểm).
a. Cho số tự nhiên n bất kỳ. Tìm tất cả các số nguyên tố p sao cho số 2
A = 2026n +1014(n + p) luôn viết được dưới dạng hiệu hai số chính phương.
b. Tìm các số nguyên x, y thoả mãn phương trình: 2 3
x − 2x = 27y Lời giải : a. Giả sử 2 2
A = a − b = (a − b)(a + b) với *
(a,b∈ N )
Do a − b và a + b có cùng tính chẵn lẻ mà A2 nên a − b và a + b đều là số chẵn
⇒ (a + b)(a − b)4hay A4. Mặt khác, 2 2 2
A = 2026n +1014(n + p) = 2028n +1016(n + p) − 2(n + n + p) Vì A4 2 2
⇒ 2(n + n + p)4 ⇒ n + n + p2 mà 2
n + n = n(n +1)2 n ∀ ∈ N
⇒ p2mà p là số nguyên tố nên p = 2. b. Ta có 2 3 2 3
x − 2x = 27y ⇔ (x −1) = 27y +1 2 2
⇔ (x −1) = (3y +1)(9y − 3y +1) (1) Đặt 2 *
(3y +1;9y − 3y +1) = d (d ∈ N ) 2
⇒ 9y − 3y +1− 3y (3y +1)d ⇒ 6
− y +1d mà 6y + 2d nên 3d ⇒ d ∈{1; } 3
Mặt khác, 3y +1không chia hết cho 3 nên d =1 2
⇒ (3y +1;9y − 3y +1) =1 2  3y +1= a
Khi đó từ (1) suy ra ta có: * 
(a,b∈ N ) 2 2 9
 y − 3y +1 = b 2 2 2 2
⇒ b = (a −1) − (a −1) +1 2 4 2 2 4 2
⇔ b = a − 3a + 3 ⇔ 4b = 4a −12a +12 2 2 2
⇔ 4b = (2a − 3) + 3 2 2
⇔ 3 = (2b − 2a + 3)(2b + 2a − 3) Mà 2 *
2b + 2a − 3 > 0 do a,b∈ N Ta có bảng giá trị sau: 2 2b − 2a + 3 1 3 2 2b + 2a − 3 3 1 a 2 1 b 1 1
Từ bảng trên ta thấy a = b =1⇒ y = 0 x = 0 2
⇒ x − 2x = 0 ⇔  x = 2 Vậy cặp ( ;
x y)thoả mãn là: (0;0); (2;0)
Document Outline

• Doc1
• HSG Toán 9 22-23Thái Nguyên