Đề thi học sinh giỏi Toán THCS cấp tỉnh năm 2020 – 2021 sở GD&ĐT Sơn La

SỞ GD&ĐT SƠN LA
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH NĂM HỌC 2020 - 2021 Môn thi: Toán ĐỀ CHÍNH THỨC Ngày thi: 14/3/2021 (Đề thi có 01 trang)
Thời gian làm bài: 150 phút, không kể thời gian phát đề 2 x x 1 3 11 x x  3
Câu 1 (4,0 điểm). Cho hai biểu thức A    và B  x  3 x  3 9  x x 1 (với x  0; x  9). 2 2
a) Tính giá trị của B tại x   .
545  2021 545  2021 b) Rút gọn A.
c) Tìm tất cả các số nguyên x để P = A.B nhận giá trị nguyên.
Câu 2 (4,0 điểm). Trong mặt phẳng tọa độ Oxy, cho đường thẳng d  : y  2m   1 x  2m và parabol P : 2 y  x ( m là tham số).
a) Tìm tọa độ các giao điểm của d  và P khi m  2 .
b) Tìm m để d  và P cắt nhau tại hai điểm phân biệt có hoành độ x , x sao cho 1 2 biểu thức 2 2
E  x  x  x x đạt giá trị nhỏ nhất. 1 2 1 2 Câu 3 (4,0 điểm). 2 2
y  2xy  8x  6x 1
a) Giải hệ phương trình  . 2 3 2
y  x  8x  x 1
b) Tìm nghiệm nguyên của phương trình 2 2
x  2 y  2xy  3y  4  0.
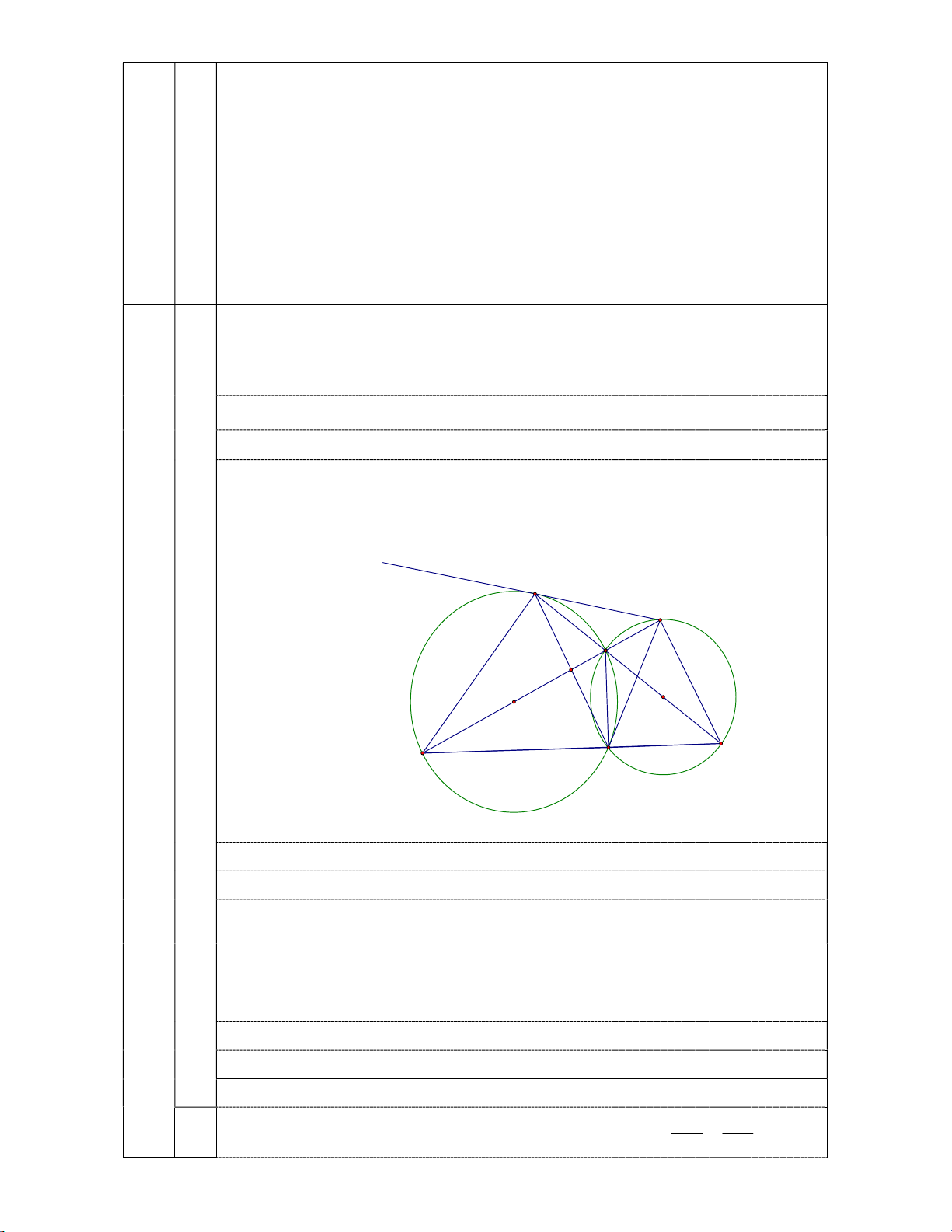
Câu 4 (6,0 điểm). Cho tam giác ABC có góc A tù. Vẽ đường tròn O đường kính AB và
đường tròn O' đường kính AC . Đường thẳng AB cắt đường tròn O' tại điểm thứ hai là
D, đường thẳng AC cắt đường tròn O tại điểm thứ hai là E .
a) Chứng minh bốn điểm B,C, D, E cùng nằm trên một đường tròn.
b) Gọi F là giao điểm thứ hai của hai đường tròn O và O' ( F khác A). Chứng
minh ba điểm B, F, C thẳng hàng và FA là phân giác của góc EF . D
c) Gọi H là giao điểm của AB và EF. Chứng minh BH.AD  AH.BD . 1 1 1
Câu 5 (2,0 điểm). Cho 3 số thực dương a, b, c thỏa mãn  
 1. Tìm giá trị nhỏ nhất 2 2 2 a b c 2 2 2 2 2 2 b c c a a b của biểu thức P    . 2 2 2 2 2 2
a(b  c ) b(c  a ) c(a  b )
-------------Hết-------------
Thí sinh không sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh:……………………………………………..Số báo danh: …………... SỞ GD&ĐT SƠN LA HƯỚNG DẪN CHẤM
KỲ THI CHỌN HỌC SINH GIỎI THCS CẤP TỈNH NĂM HỌC 2020 - 2021 ĐỀ CHÍNH THỨC Môn: Toán (HD chấm có 04 trang) Câu Ý Nội dung Điểm Ta có: 2 2 x  
545  2021 545  2021
245  2021  245  2021     90 2 2021 90 2 2021  0,5 52025  202  1.a
545  202145  2021 1 180   9 20
Thay x  9 vào biểu thức B ta được: x  3 9  3 3  3 B     0 0,5 x 1 9 1 3 1 2 x x 1 3 11 x A    x  3 x  3 9  x
2 x  x  3   x   1  x  3 11 x  3 0,5  1  x 3 x 3 1.b
2x  6 x  x  3 x  x  3 11 x  3   0,5 x  3 x  3 3 x x  x  x 3 3 9   3 x    với x  0, x  9 0,5
x  3 x  3  x  3 x  3 x  3 3 x x  3 3 x 3 x   1  3 Ta có: P  . A B  . = = = x  3 x 1 x 1 x 1 0,5 3 3  x 1 1.c  3 P là số nguyên 
là số nguyên  3 x   1 0,5 x 1 Hay  x   1 Ư(3) = {  1;  3 } 0,5 ...  x 0;  4
Khi m  2 đường thẳng (d) có dạng: y  5x  4 0,25
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình:   0,25 2 2.a x 1 2 2
x  5x  4  x  5x  4  0   x  4
Với x  1  y  1; x  4  y  16 . 0,25
Vậy tọa độ giao điểm của d  và P là: (1;1) ; 4;16 . 0,25
Hoành độ giao điểm của (d) và (P) là nghiệm của phương trình: 0,25 2 x  2m   1 x  2m 2  x  2m   1 x  2m  0
Tính được    m  2 2 1 0,25 1
* (P) và (d) cắt nhau tại hai điểm phân biệt    0  m  0,5 2 x  x  2m 1
* Áp dụng hệ thức Vi-ét, ta có: 1 2  x .x  2m 0,5  2b 1 2 Do đó: 2 2
E  x  x  x .x   m  2 2 2 1  3.2m  4m  2m 1 0,5 1 2 1 2 2  1  3 3 0,5  2m      , với mọi m   .  2  4 4 3 1 0,5 Min E  khi m  4 4 2 2
y  2xy  8x  6x 1 (1) a)  2 3 2
y  x  8x  x 1 (2)
Từ phương trình (1) cộng vào 2 vế với 2 x , ta được: 0,5 2 2 2
y  2xy  x  9x  6x 1
 x  y2   x  2  x  y2   x  2 3 1 3 1  0 0,5  x  y  3x   1  x  y  3x  
1  0  1 2x  y4x  y   1  0 1   2x  y  0  y  1 2x    4x y 1 0      y  4x 1
3a + Trường hợp 1: y  4x1 thế vào phương trình (2) ta được:  x  2 3 2 2 3 2 4
1  x  8x  x 1  16x  8x 1  x  8x  x 1 0,5 x  0 3 2 x 8x 7x 0       x  1  x  7 
Ta tìm được nghiệm  ;
x y là (0; - 1); (1; 3); (7; 27)
+ Trường hợp 2: y  1 2x thế vào phương trình (2) ta được: 0,5   x2 3 2 1 2  (x  8x  x 1) x  0 2 3 2 3 2 4x 4x 1 x 8x x 1 x 4x 3x 0              x  1  x  3  Tìm được nghiệm  ;
x y là: (0; 1); (-1; 3); (-3; 7)
Vậy hệ phương trình có tập nghiệm là: S  
 0; 1; 0; 1; 1;3;  1  ;3; 7;27;  3  ;7
Biến đổi phương trình: 2 2
x  y  xy  y     2 2 x  xy  y  2 2 2 3 4 0 2  y  3y  4  0 0,5 2
  x  y   y   1  y  4  0 3
  y   y     x  y2 1 4  0 0,5
3b   4  y 1, vì y nguyên nên y4;3;2;1;0; 1 0,5 Suy ra các cặp  ;
x y nguyên thỏa mãn phương trình là: 4; 4;  1  ; 
1 ; 5; 3; 1; 3; 2; 0;  2  ; 0 0,5 Hình vẽ đúng: x E D A H O O' 0,5 4a B C F 4 Lập luận có  0 AEB  90 0,5 Lập luận có  0 ADC  90 0,5
Suy ra bốn điểm B, C, D, E cùng nằm trên một đường tròn đường 0,5 kính BC. Ta có  AFB   0
AFC  90 (Góc nội tiếp chắn nửa đường tròn) suy ra  AFB   0 AFC  180 0,5
Suy ra ba điểm B, F, C thẳng hàng 4b  AFE   ABE (cùng chắn  AE ) và  AFD   ACD (cùng chắn  AD ) 0,5 Mà  ECD   EBD (cùng chắn 
DE của tứ giác BCDE nội tiếp) 0,5 Suy ra:  AFE  
AFD => FA là phân giác của góc  EFD 0,5 AH EH
4c C/m được EA là phân giác của tam giác DHE và suy ra  0,5 AD ED (1)
Xét tam giác HED có EA là phân giác trong của tam giác. Mặt khác 0,5
BE  EA nên BE là phân giác ngoài của tam giác HED BH EH
EB là phân giác ngoài của tam giác DHE suy ra  (2) 0,5 BD ED AH BH Từ (1), (2) ta có:   AH.BD  BH.AD 0,5 AD BD 1 1 1 Ta có: P     1 1   1 1   1 1  a  b  c  0,5  2 2   2 2   2 2   c b   c a   a b  1 1 1 Đặt  ; x  y;  z thì 2 2 2
x  y  z  1 và 0  x, y, z  1. a b c 0,5 2 2 2 x y z x y z P       2 2 2 2 2 2 2 2 2 y  z z  x x  y x(1 x ) y(1 y ) z(1 z )
Áp dụng bất đẳng thức Côsi cho 3 số dương ta có: 3 2 2 2       2 2 2 1 2 2 2 1 2x 1 x 1 x 4
x (1 x )  .2x (1 x )(1 x )     2 2 3 27   5 5 2 0,5 2 2 x 3 3 2  x(1 x )    x (1) 2 3 3 x(1 x ) 2 2 2 y 3 3 z 3 3 Tương tự: 2 2  y (2);  z (3) 2 2 y(1 y ) 2 z(1 z ) 2 3 3 3 3 Từ (1); (2); (3) ta có 2 2 2 P  (x  y  z )  2 2 1
Đẳng thức xảy ra  x  y  z  hay a  b  c  3 3 0,5 3 3
Vậy giá trị nhỏ nhất của P là
xảy ra khi a  b  c  3 2
(Lưu ý: Học sinh làm theo đáp án khác và đúng thì giáo viên vẫn chấm điểm đối đa)
-------------Hết-------------