Đề thi HSG Toán 9 lần 2 năm 2023 – 2024 trường THCS Đắk Ơ – Bình Phước

TRƯỜNG THCS ĐĂK Ơ
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
Năm học: 2023 - 2024 ĐỀ CHÍNH THỨC
Đề thi môn : Toán - LẦN 2 (Đề thi gồm 01 trang)
Thời gian: 150 phút ( không kể thời gian giao đề) Câu 1. (5,0 điểm)  −   − − −  1. Cho biểu thức x 3 x x 3 x 2 9 = 1−  : x A  + −   x 9   2 x 3 x x x 6  − − + + −    
a) Tìm x để biểu thức A có nghĩa và rút gọn biểu thức A .
b) Tính giá trị của A khi x = 22+12 2 2. Cho x y
x; y thỏa mãn 0  x 1; 0  y 1 và   1 . 1 x 1 y
Tính giá trị của biểu thức 2 2
P  x  y  x  xy  y .
3. Cho ba số dương a, b, c là các số thực dương. Chứng minh rằng: a b c 3 + + ≥
b + c c + a b + a 2 Câu 2. (5,0 điểm) 3 2
1. Giải phương trình: 3x −17x −8x + 9 + 3x − 2 − 7 − x = 0 2 2  2x 2 y + =  1
2. Giải hệ phương trình: ( y + )2 1 ( x + )2 1 3 
 xy − x − y = 1
Câu 3: ( 5,0 điểm) Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) và trực tâm là H.
Lấy điểm M thuộc cung nhỏ BC.
a) Xác định vị trí của điểm M sao cho tứ giác BHCM là hình bình hành.
b) Với M lấy bất kì thuộc cung nhỏ BC; gọi N, E lần lượt là các điểm đối xứng của M qua AB
và AC. Chứng minh tứ giác AHBN nội tiếp.
c) Chứng minh ba điểm N, H, E thẳng hàng.
d) Xác định vị trí của điểm M thuộc cung nhỏ BC để cho NE có độ dài lớn nhất.
Câu 4. (2,0 điểm) Cho tam giác ABC nhọn nội tiếp đường tròn (O) . Một điểm M di động trên cung
nhỏ BC . Từ M kẻ MH,MK lần lượt vuông góc AB, AC (H ∈ AB, K ∈ AC) .
1. Chứng minh MB ∆
C đồng dạng MH ∆ K
2. Tìm vị trí của M để HK lớn nhất. Câu 5. (3,0 điểm)
1. Tìm tất cả các nghiệm nguyên của phương trình 2 2 2
x + 2022x + 2023y + y = xy + 2023xy + 2024 .
2. Tìm các số nguyên dương sao cho 2 2
n + 2n + n + 2n +18 + 9 là số chính phương. - - - HẾT - - -
• Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
• Giám thị coi thi không giải thích gì thêm.
TRƯỜNG THCS ĐĂK Ơ
KỲ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
Năm học: 2022 - 2023
Đề thi môn : Toán
ĐÁP ÁN VÀ THANG ĐIỂM Câ Ý LỜI GIẢI Điểm u 1  x − x   x − x − − x  Cho biểu thức 3 3 2 9 A = 1−  :  + −   x 9    −
2 − x 3+ x x + x −    6 
a) Tìm x để biểu thức A có nghĩa và rút gọn biểu thức A . 1 x ≥ 0  x −2 ≠  0 x ≥ 0 +) ĐK:   0,5 x − 9 ≠ 0 ⇔ x ≠ 4 (*)   − − − x ≠  9  x 3 x 2 9 x + − ≠ 0
2− x 3+ x x + x −6  x ( x −3)  +)
( x + 3)( x − 3) + ( x + 2)(2 − x) + 9 1 − x A 1,5  (  = − 
x − 3)( x +3) : 
(2 − x)( x + 3)  3 x − 2 3 = : = x + 3 3+ x x − 2
b) Tính giá trị của A khi x = 22 +12 2 3 3 3 1 2 0,5 A = = = = = 22 +12 2 − 2 (2+3 2)2 2 + 3 2 − 2 2 2 − 2 0,5 2 Cho x y
x; y thỏa mãn 0  x 1; 0  y 1 và   1 . 1 x 1 y
Tính giá trị của biểu thức 2 2
P  x  y  x  xy  y . 0,25
Ta có P  x  y  x  xy  y  x  y  x  y2 2 2  3xy . x y Thay 
 1 2x  2y 1 3xy vào biểu thức P ta được 1 x 1 y
P  x  y  x  y2  x  y  x  y  x  y 2 2 1
1  x  y  x  y 1  1 0,5
(vì x y 1). Giải thích x  y 1.
Từ giả thiết ta có x ; y là các số dương mà x y   1 , nên ta 1 x 1 y 1 x 1 y 0,25  x 2x1     1 1   0 x  có 1x  1x  2     
 x  y 1.  y 2y 1  1  1   0  1  1 y y  y      2 Vậy P 1.
3 Cho ba số dương a, b, c là các số thực dương. Chứng minh rằng: a b c 3 + + ≥
b + c c + a b + a 2
Bất đằng thức trên luôn đúng vì Ta có bđt phụ sau với x,y,z > 0 ta chứng minh được. 0,25 1 1 1
(x + y + z)( + + ) ≥ 9 x y z ⇔ ( x y + ) + ( x z + ) + ( y z + ) ≥ 6 y x z x z y / / / x y + ≥ 2; x z + ≥ 2; y z luon dung vi + ≥ 2 y x z x z y
Dấu = xay ra khi x = y = z (*) a b c 3 a b c 3 0,25 + + ≥ ⇔ +1+ +1+ +1≥ + 3
b + c c + a b + a 2 b + c c + a b + a 2 1 1 1 1 9
⇔ [(b + c) + (c + a) + (b + a)][ + + ] ≥ 2
b + c c + a b + a 2 0,25 1 1 1
⇔ [(b + c) + (c + a) + (b + a)][ + + ] ≥ 9
b + c c + a b + a
Bất đằng thức luôn đúng vì theo BĐT (*) Dấu = xảy ra khi a = b = c. 0,25
2 1 Giải phương trình 3 2
3x −17x −8x + 9 + 3x − 2 − 7 − x = 0
. ĐKXĐ: 2≤x≤7. 0,5 3
PT (1)⇔ ( x − − )−( − x − ) 3 2 3 2 4 7
1 + 3x −17x −8x +12 = 0
⇔ ( 3x −2 −4)−( 7− x − )1+(3x −2)(x −6)(x +1) = 0 0,5 3x −18 6 − x ⇔ −
+ (3x − 2)(x − 6)(x +1) = 0 3x − 2 + 4 7 − x +1 (x ) 3 1 6 (3x 2)(x 1) ⇔ − + + − + =   0 0,5  3x − 2 + 4 7 − x +1  Vì 2 ≤ x ≤ 7 nên 3 1 +
+ (3x − 2)(x +1) > 0 0,5 3 3x − 2 + 4 7 − x +1
Suy ra x −6 = 0 ⇔ x = 6(t / m) 0,25
KL: PT (1) có nghiệm duy nhất x = 6. 0,25 2 2  2x 2y 2 + =  1
Giải hệ phương trình: ( y + )2 1 (x + )2 1 . 3 
 xy − x − y = 1 x ≠ 1, − y ≠ 1 − 0.25 ( )
⇔ xy = xy + x + y + ⇔ xy = (x + )( y + ) x y 1 2 4 1 4 1 1 ⇔ ⋅ = y +1 x +1 4 0,5 Đặt x = ; y a = b y +1 x +1  0,5 2 2 1 a + b =  1  a = b = 2   2  Ta có 1 a + b = Giải hệ ta có  1  4 b = a = −  2
Với a=b =1/2 ta tìm được ( x,y) = (1;1); 0,5
Với a=b = -1/2 ta tìm được ( x,y) = (-1/3;-1/3) 0,5
KL: Hệ phương trình có 2 nghiệm (1;1); (-1/3;-1/3) 0,25 3
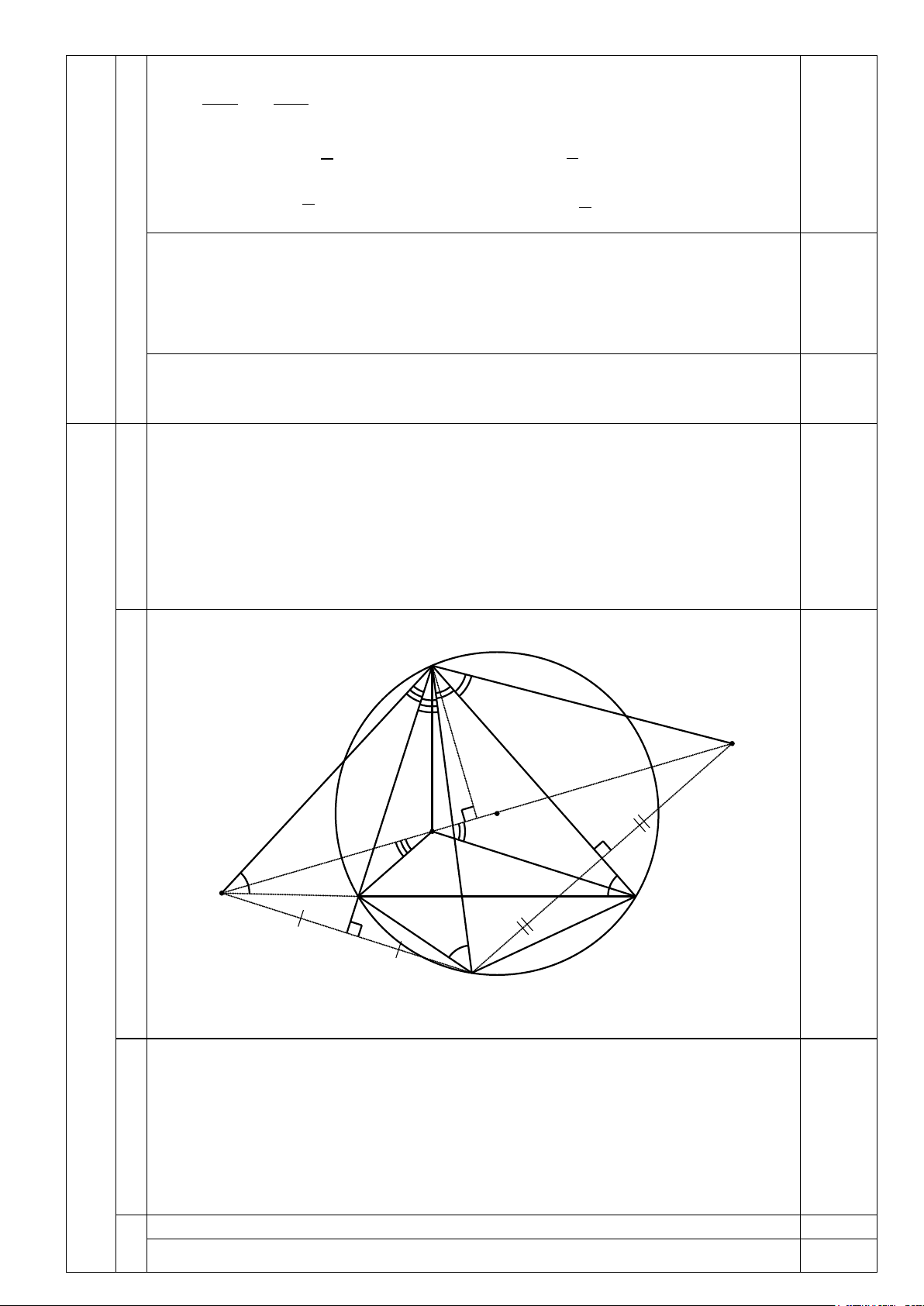
Cho tam giác ABC có ba góc nhọn nội tiếp đường tròn (O) và trực tâm là H. Lấy
điểm M thuộc cung nhỏ BC.
a) Xác định vị trí của điểm M sao cho tứ giác BHCM là hình bình hành.
b) Với M lấy bất kì thuộc cung nhỏ BC; gọi N, E lần lượt là các điểm đối xứng
của M qua AB và AC. Chứng minh tứ giác AHBN nội tiếp.
c) Chứng minh ba điểm N, H, E thẳng hàng.
d) Xác định vị trí của điểm M thuộc cung nhỏ BC để cho NE có độ dài lớn nhất. A 4 1 3 2 E K 2 O 1 H 1 1 B N C 1 M 1
a) Xác định vị trí của điểm M sao cho tứ giác BHCM là hình bình hành.
Ta có: BH ⊥ AC; CH ⊥ AB (vì H là trực tâm tam giác ABC) 0,5
Tứ giác BHCM là hình bình hành ⇔ BH // MC và CH // MB 0,5 ⇔ AC ⊥ MC và AB ⊥ MB 0,5
⇔ AM là đường kính của (O) 0,5
⇔ M là điểm đối xứng của A qua O.
2 b) Chứng minh tứ giác AHBN nội tiếp. Ta có:  =  M
N (T/c đối xứng trục) 0,25 1 1  =  M
C (góc nội tiếp cùng chắn cung AB) 0,25 1 1 ⇒  =  N C , mà  +  0 AHB C =180 1 1 1 0,25 Do đó:  +  0
AHB N =180 ⇒ Tứ giác NAHB nội tiếp. 0,25 1
3 c) Chứng minh ba điểm N, H, E thẳng hàng.
Tứ giác NAHB nội tiếp ⇒  =  H A , mà  = 
A A (T/c đối xứng trục)⇒  =  H A . 0,25 1 1 1 2 1 2 0,25
Chứng minh tương tự, ta cũng có:  =  H A 2 3 Ta có:  +  0 BAC BHC =180 0,25 Do đó:  =  +  +  NHE H H CHB =  +  +  A A CHB =  +  0
BAC BHC =180 ⇔ N, H, E 1 2 2 3 thẳng hàng 0,25
4 d) Xác định vị trí của điểm M thuộc cung nhỏ BC để cho NE có độ dài lớn nhất. Ta có:  = 
NAE 2BAC . Kẻ AK ⊥ NE tại K 0,25
Ta có: AM = AN; AM = AE (Tính chất đối xứng trục)
⇒ AE = AN ⇒ ∆ ANE cân. Mà: AK là đường cao
⇒ AK là trung tuyến, là phân giác ⇒  = 
NAE 2NAK; NE = 2NK NE ⇒ NK = 2 0,25 Do đó:  =  BAC NAK
Tam giác KAN vuông tại K ⇒ NK = AN.sin  NAK Do đó: NE = 2AN. sin  NAK = 2AM.sin  BAC ≤  2 .
R sin BAC (vì AM ≤  2 ; R sin BAC : 0,25 Không đổi)
Do đó: NE lớn nhất ⇔ AM lớn nhất
⇔ AM là đường kính của đường tròn (O)
⇔ M đối xứng với A qua O 0,25
Vậy khi M là điểm đối xứng của A qua O thì NE lớn nhất. 4
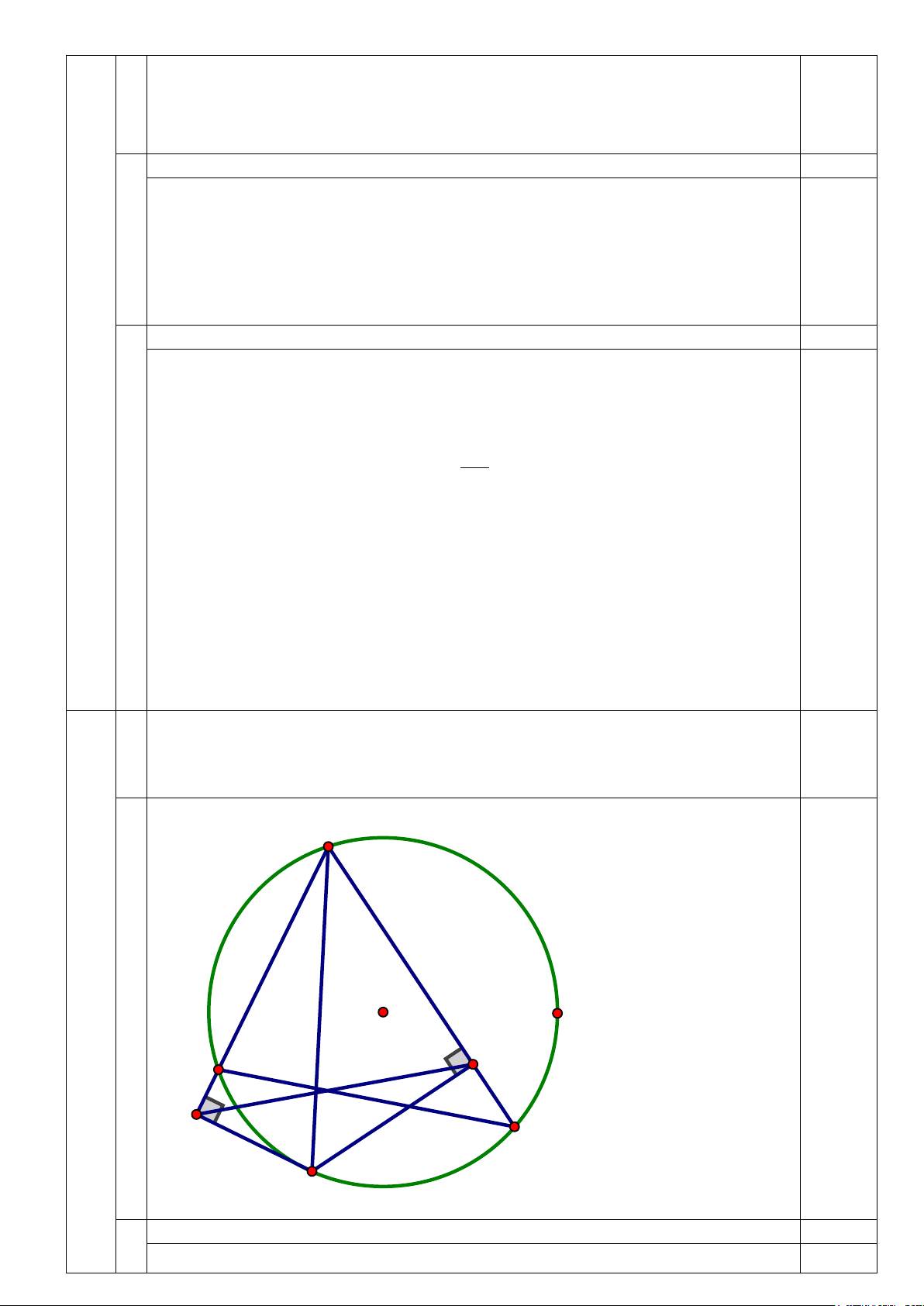
Cho tam giác ABC nhọn nội tiếp đường tròn (O) . Một điểm M di động
trên cung nhỏ BC . Từ M kẻ MH,MK lần lượt vuông góc AB, AC
(H ∈ AB, K ∈ AC) . A O B K H C M
1 Chứng minh MB ∆
C đồng dạng MH ∆ K
+) Tứ giác AHMK nội tiếp suy ra  =  =  MBC MAC MHK 0,50
+) Tứ giác ABMC nội tiếp suy ra  =  =  MCB MAB MKH 0,50 +) Suy ra MB ∆
C đồng dạng MH ∆ K 0,25
2 Tìm vị trí của M để HK lớn nhất. 0,50
CM câu trên suy ra BC MB = mà BC MB ≥ MH ⇒
≥ 1⇒ BC ≥ HK 0,50 HK MH HK
Đẳng thức xảy ra khi H trùng B⇒  0
ABM = 90 hay M đối xứng với A qua O. 0,25
5 1 Tìm tất cả các nghiệm nguyên của phương . trình 2 2 2
x + 2022x + 2023y + y = xy + 2023xy + 2024 (1) ( ) 1 ⇔ ( 2
x + 2022x − 2023) 2
− 2023y (x − ) 1 − y (x − ) 1 =1 0,25 ⇔ (x − ) 1 ( 2
x + 2023− 2023y − y) =1 0,25
Vì x,y nguyên nên các thừa số của vế trái là ước của 1 do đó ta có hai trường hợp: x = 2 x −1 = 1 +)  x = 2  ⇔  ⇔ 0,50 2 2024 
x + 2023 − 2023y − y = 1
y = 1∨ y = − (l) y =1  2023 x = 0 x −1 = 1 −  x = 0 +)  ⇔  ⇔ 2 2024  0,50
x + 2023 − 2023y − y = 1 −
y = 1∨ y = − (l) y =1  2023
Vậy phương trình có hai nghiệm: (2; ) 1 ,(0; ) 1 .
2 Tìm các số nguyên dương sao cho 2 2
n + 2n + n + 2n +18 + 9 . là số chính phương. Do 2 2
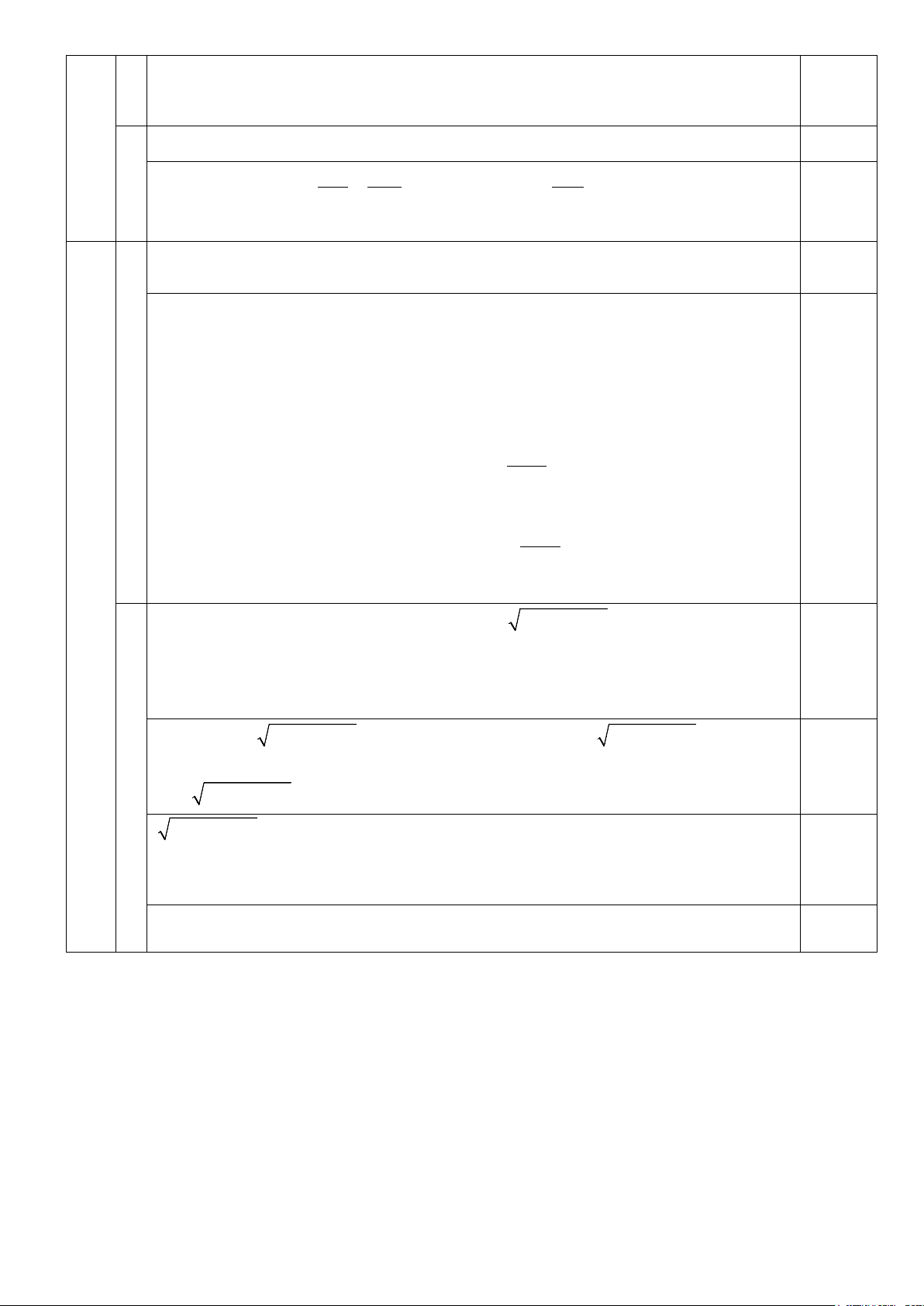
n + 2n + n + 2n +18 + 9 là số chính phương nên 2n + 2n +18 là số tự nhiên 0,50 Đặt 2
n + 2n +18 = k2 (k là số tự nhiên) 2 2
n + 2n +18 = k ⇔ (k + n +1)(k − n −1) =17 0,75 k = 9 ⇒  n = 7
KL: n = 7 thỏa mãn bài toán. 0,25 - - - HẾT - - -