Đề thi HSG Toán 9 năm 2016 – 2017 phòng GD&ĐT thị xã Giá Rai – Bạc Liêu

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chọn học sinh giỏi môn Toán năm 2016 – 2017 phòng GD&ĐT thị xã Giá Rai – Bạc Liêu giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.

18 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

4 trang 6 tháng trước

Tác giả:

Profile Hà Việt Anh
Họ và tên thí sinh:……………………..………….. Chữ ký giám thị 1:
Số báo danh:……………………………..………... …………….………………..
PHÒNG GD&ĐT THỊ XÃ GIÁ RAI KỲ THI CHỌN HSG LỚP 9 VÒNG THỊ XÃ
NĂM HỌC 2016 - 2017
* Môn thi: TOÁN
* Ngày thi: 25/12/2016
* Thời gian: 150 phút (Không kể thời gian giao đề)
ĐỀ
Câu 1: (5 điểm)
a) Chứng minh rằng tích của 4 số nguyên dương liên tiếp không thể là một số
chính phương.
b) Cho:
5. 5 1 6. 3 2
nn nn n
M
. Chứng minh: 91;
Mn
Câu 2: (5 điểm)
a) Giải phương trình:
32
10 x + 1 = 3 x + 2
b) Giải hệ phương trình:
3
3
x + 1 = 2y
y + 1 = 2x
Câu 3: (5 điểm)
a) Cho biểu thức:
21
1

B
x
x
. Chứng minh: 322B với 01
x
b) Cho hai số dương a, b thỏa mãn:
22ab
. Tìm giá trị nhỏ nhất của biểu
thức:
11
ab
P
.
Câu 4: (5 điểm)
Cho đường tròn (O; R); AB và CD là hai đường kính khác nhau của đường tròn.
Tiếp tuyến tại B của đường tròn (O; R) cắt các đường thẳng AC, AD thứ tự tại E và F.
a) Chứng minh tứ giác ACBD là hình chữ nhật.
b) Chứng minh

A
CD CBE∽
đồng dạng với nhau.
c) Chứng minh tứ giác CDFE nội tiếp.
d) Gọi S; S
1
; S
2
theo thứ tự lần lượt là diện tích của
,,
A
EF BCE BDF
.
Chứng minh:
12
SS S.
--- HẾT ---
(Gồm 01 trang)
ĐỀ CHÍNH THỨC
PHÒNG GD&ĐT THỊ XÃ GIÁ RAI KỲ THI CHỌN HSG LỚP 9 VÒNG THỊ XÃ
NĂM HỌC 2016 - 2017
* Môn thi: TOÁN
HƯỚNG DẪN CHẤM
Câu Nội dung
Số
điểm
1
(5 điểm)
a)
Gọi:
;1;2;3 nn n n
là 4 số nguyên dương liên tiếp
Ta có:
123 Ann n n
22
332 nnnn
0,25đ
2
22
323 nn nn
1,0đ
22
22
331 nnAnn
1,0đ
Vậ
y
: A khôn
g
thể là một số chính phươn
g
0,25đ
b)
Ta có:
5. 5 1 6. 3 2
nn nn n
M
25 18 12 5 7
nn nn
1,0đ
Và:
25 12 18 5 13
nn nn
M
1,0đ
Mà:
7;13 1
0,25đ
Vậy: 91;
Mn
0,25đ
2
(5 điểm)
a)
ĐK:
1x
0,25đ
Đặt:
2
1
;0,0
1



ax
ab
bxx
22 2
2ab x
0,25đ
22
10 3ab a b
0,25đ
33 0 abab
0,25đ
3
3
ab
ba
0,25đ
Với:
3ab
, thì:
2
13 1
x
xx
2
91080xx
(pt vô nghiệm)
0,5đ
Với:
3ba
, thì:
2
31 1
x
xx
2
10 8 0 xx
533x
0,5đ
(Gồm 03 trang)
ĐỀ CHÍNH THỨC
Vậy:
533S
0,25đ
b)
Ta có:
3
3
12
12


x
y
yx
33
2
x
yyx
0,25đ


22
20 xyx xyy
0,25đ
Mà:
2
2
22
3
220
24

 


yy
xxyy x
0,25đ
0xy
0,25đ

xy
0,25đ
Ta có phươn
g
t
r
ình:
3
210xx
2
110 xxx
0,25đ
2
10
10


x
xx
0,25đ
1
15
2

x
x
0,5đ
Vậ
y
: Hệ phươn
g
t
r
ình có 3 n
g
hiệm
15 15
1
22
;;
1
15 15
22

 




 




xx
x
y
yy
0,25đ
3
(5 điểm)
a)
Ta có:
21
1

B
x
x
21
213
1




xx
1,0đ
21
3
1

xx
xx
0,75đ
Áp dụng bất đẳng thức Côsi cho 2 số dương
21
;
1
x
x
x
x
. Ta được:
21
2. 3322
1

xx
B
xx
0,5đ
Vậy:
322;0 1
B
x
0,25đ
Ta có:
 
22
04ab ab ab
0,25đ
4

ab
ab a b
0,5đ
11 4

abab
0,25đ
b)
4

P
ab
0,25đ
Mà: 22ab
0,25đ
2P
. Dấu “=” xảy ra

2
0
22


ab
ab
0,5đ
2ab
0,25đ
Vậy: 22MinP a b
0,25đ
4
(5 điểm)
0,25đ
a)
Ta có:
0
90ACB ADB DAC
(góc nội tiếp chắn nửa (O))
0,5đ
A
CBD
là hình chữ nhật (tứ giác có 3 góc vuông)
0,5đ
b)
Ta có :
A
DCB
(ACBD là hình chữ nhật)
0,25đ

A
DCB
(liên hệ giữa cung và dây cung)
0,25đ

A
CD CBE (góc nội tiếp với góc tạo bởi tia tiếp tuyến và dây chắn
2 cun
g
bằn
g
nhau)
0,25đ

vuông
A
CD ∽
vuông
CBE
(1 góc nhọn)
0,75đ
c)
Ta có :
vuông
A
CD ∽
vuông
CBE
(chứng minh trên)
0,25đ

A
DC CEB
0,5đ
CDFE
nội tiếp
0,25đ
d)
Ta có:
//CB AF
 CBE AFE∽
0,25đ
2
1
2

S
EB
SEF
1

S
EB
SEF
0,25đ
Tươn
g
tự :
2
S
BF
SEF
0,25đ
12
1
SS
SS
0,25đ
12
SS S
0,25đ
-- HẾT---
F
E
D
B
O
A
C
| 1/4
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Họ và tên thí sinh:……………………..…………..
Chữ ký giám thị 1:
Số báo danh:……………………………..………...
…………….………………..
PHÒNG GD&ĐT THỊ XÃ GIÁ RAI KỲ THI CHỌN HSG LỚP 9 VÒNG THỊ XÃ
NĂM HỌC 2016 - 2017 ĐỀ CHÍNH THỨC * Môn thi: TOÁN (Gồ m 01 tran g)
* Ngày thi: 25/12/2016
* Thời gian: 150 phút (Không kể thời gian giao đề) ĐỀ Câu 1: (5 điểm)
a) Chứng minh rằng tích của 4 số nguyên dương liên tiếp không thể là một số chính phương. b) Cho:
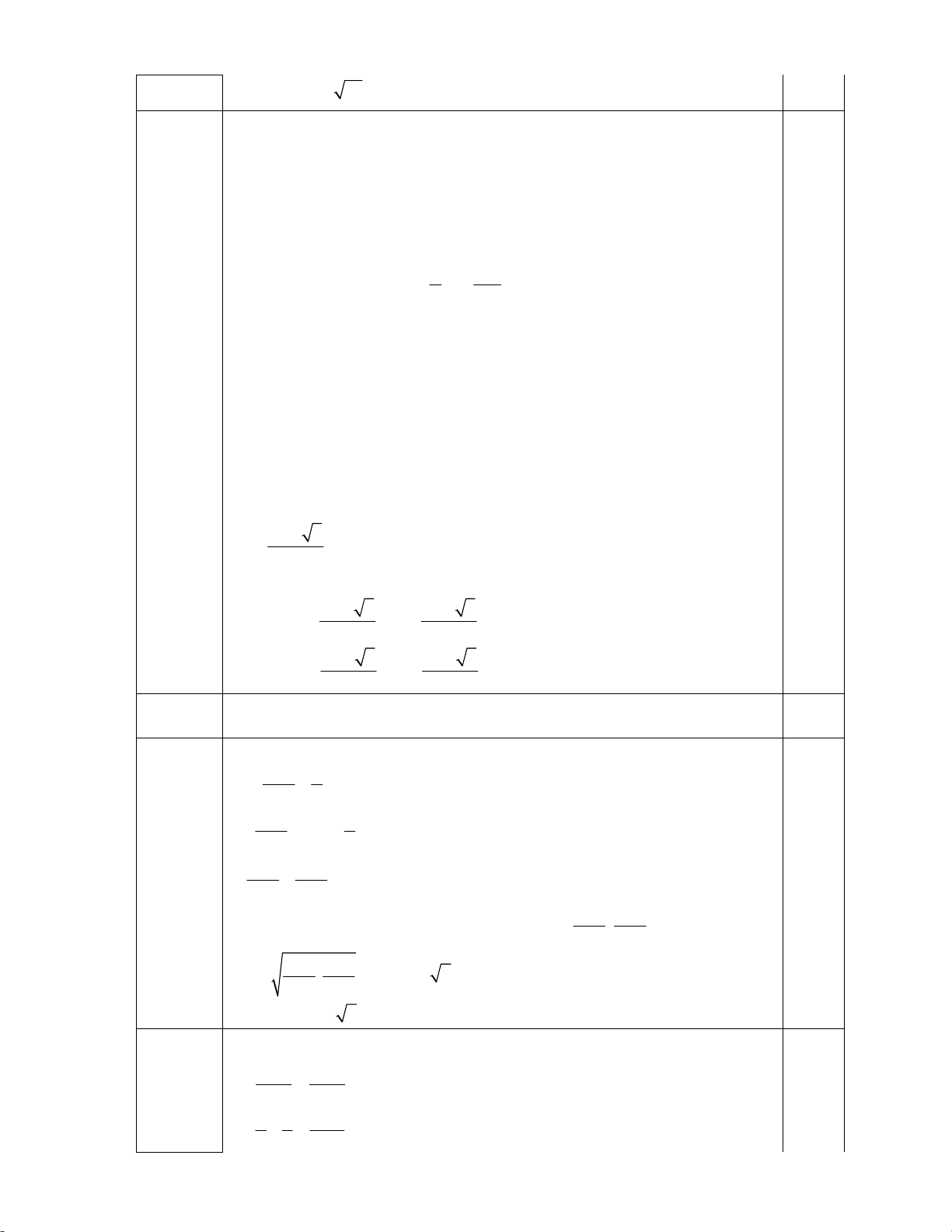
 5n.5n  
1  6n.3n  2n M
. Chứng minh: M91;  n Câu 2: (5 điểm) a) Giải phương trình: 3  2 10 x + 1 = 3 x + 2 3 x + 1 = 2y
b) Giải hệ phương trình:  3 y + 1 = 2x Câu 3: (5 điểm) a) Cho biểu thức: 2 1 B
 . Chứng minh: B  3 2 2 với 0  x 1 1 x x
b) Cho hai số dương a, b thỏa mãn: a b  2 2 . Tìm giá trị nhỏ nhất của biểu thức: 1 1 P   . a b Câu 4: (5 điểm)
Cho đường tròn (O; R); AB và CD là hai đường kính khác nhau của đường tròn.
Tiếp tuyến tại B của đường tròn (O; R) cắt các đường thẳng AC, AD thứ tự tại E và F.
a) Chứng minh tứ giác ACBD là hình chữ nhật.
b) Chứng minh ACD ∽ CBE đồng dạng với nhau.
c) Chứng minh tứ giác CDFE nội tiếp.
d) Gọi S; S1; S2 theo thứ tự lần lượt là diện tích của AEF, BCE, BDF .
Chứng minh: S  S  S . 1 2 --- HẾT ---
PHÒNG GD&ĐT THỊ XÃ GIÁ RAI KỲ THI CHỌN HSG LỚP 9 VÒNG THỊ XÃ
NĂM HỌC 2016 - 2017 ĐỀ CHÍNH THỨC * Môn thi: TOÁN (Gồ m 03 trang) HƯỚNG DẪN CHẤM Số Câu Nội dung điểm 1 (5 điểm) Gọi: ;
n n 1;n  2;n  3 là 4 số nguyên dương liên tiếp Ta có:
A nn  
1 n  2n  3   2 n n 2 3
n  3n  2 a) 0,25đ
 n n2 2   2 3 2 n  3n 1,0đ
 n n2  A  n n  2 2 2 3 3 1 1,0đ
Vậy: A không thể là một số chính phương 0,25đ Ta có:
 5n.5n  
1  6n.3n  2n M
 25n 18n  12n 5n 7 1,0đ b) Và:
 25n 12n  18n  5n M  13 1,0đ Mà:7;13 1 0,25đ Vậy: M 91;  n 0,25đ 2 (5 điểm) ĐK: x  1  0,25đ
a x 1 Đặt: 
;a  0,b  0 2
b x x 1 2 2 2
a b x  2 0,25đ  ab   2 2 10 3 a b  0,25đ
 a 3b3a b  0 0,25đ a  3b a)   0,25đ b  3a
Với: a  3b , thì: 2
x 1  3 x x 1 2
 9x 10x  8  0 (pt vô nghiệm) 0,5đ
Với: b  3a , thì: 2
3 x 1  x x 1 2
x 10x  8  0  x  5 33 0,5đ
Vậy: S  5 33 0,25đ Ta có: 3
x 1 2y  3
y 1  2x 3 3
x y  2 y x 0,25đ
 x y 2 2
x xy y  2  0 0,25đ 2 2 Mà:  y  3y 2 2
x xy y  2  x    2  0   0,25đ  2  4
x y  0 0,25đ  x y 0,25đ Ta có phương trình: 3
x  2x 1  0 2 b)  x  
1 x x   1  0 0,25đ x 1  0  0,25đ 2
x x 1  0 x 1  1   5  0,5đ x   2
Vậy: Hệ phương trình có 3 nghiệm  1 5  1 5 x  x  x  1  2  2  ;  ;  0,25đ  y  1  1 5  1 5 y y   2    2 3 (5 điểm) Ta có: 2 1 B   1 x x  2   1    2  1  3     1,0đ 1 x   x  2x 1 x a)    3 0,75đ 1 x x x
Áp dụng bất đẳng thức Côsi cho 2 số dương 2 1 x ; . Ta được: 1 x x 2x 1  x B 2 .  3  3 2 2 0,5đ 1 x x
Vậy: B  3  2 2 ;0  x  1 0,25đ
Ta có: a b2   a b2 0  4ab 0,25đ a b 4   0,5đ ab a b 1 1 4    0,25đ a b a b 4  P 0,25đ a b b)
Mà: a b  2 2 0,25đ
a b2  0
P  2 . Dấu “=” xảy ra   0,5đ
a b  2 2
a b  2 0,25đ
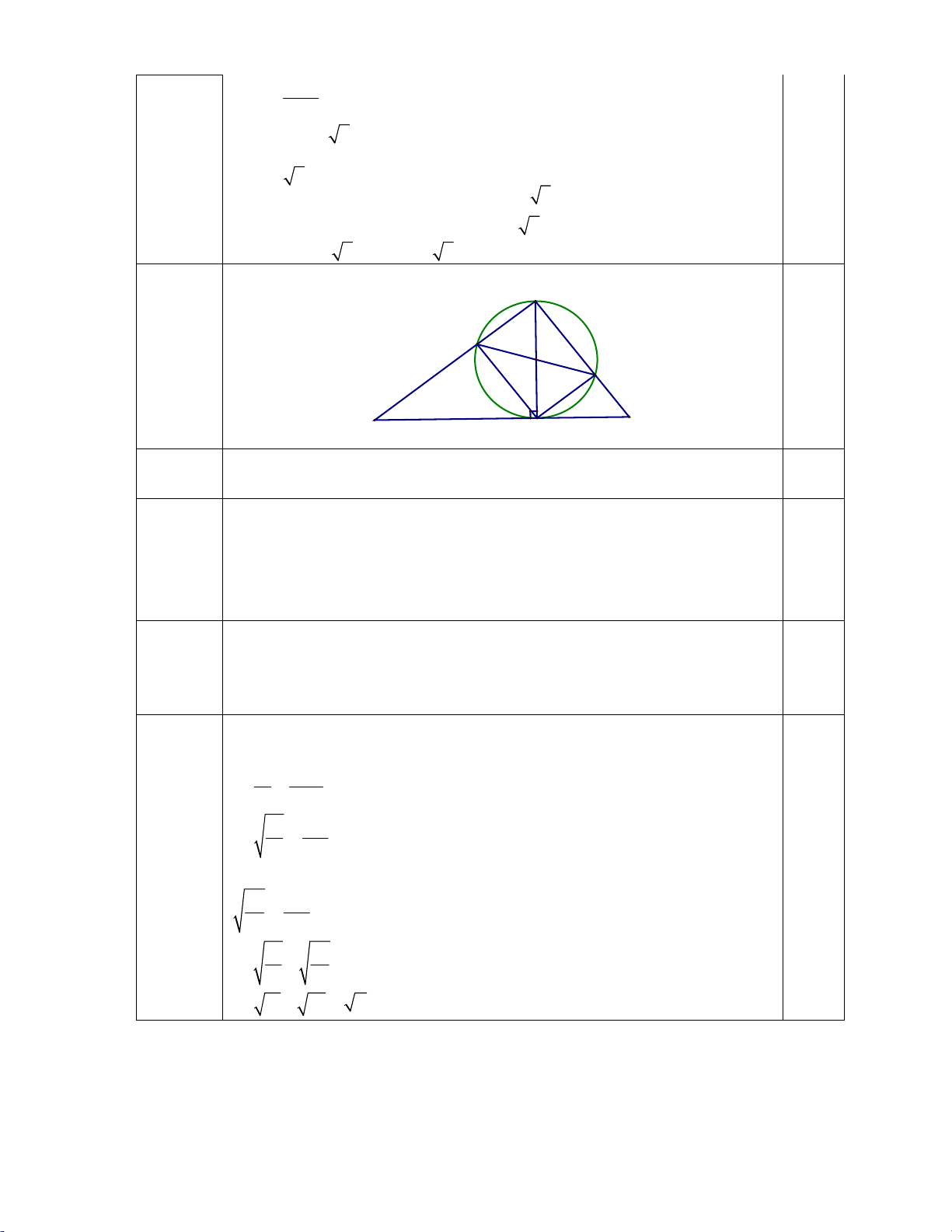
Vậy: MinP  2  a b  2 0,25đ 4 (5 điểm) A C O 0,25đ D E F B a) Ta có:    0
ACB ADB DAC  90 (góc nội tiếp chắn nửa (O)) 0,5đ
ACBD là hình chữ nhật (tứ giác có 3 góc vuông) 0,5đ
Ta có : AD CB (ACBD là hình chữ nhật) 0,25đ  
AD CB (liên hệ giữa cung và dây cung) 0,25đ b)  
ACD CBE (góc nội tiếp với góc tạo bởi tia tiếp tuyến và dây chắn 0,25đ 2 cung bằng nhau)
  vuông ACD ∽  vuôngCBE (1 góc nhọn) 0,75đ Ta có :
 vuông ACD ∽  vuôngCBE (chứng minh trên) 0,25đ c)  
ADC CEB 0,5đ  CDFE nội tiếp 0,25đ
Ta có: CB / / AF
 CBE ∽ AFE 0,25đ 2 S EB 1   2 S EF S EB 1   0,25đ S EF d) Tương tự : S BF 2  0,25đ S EF S S 1 2   1 0,25đ S S
S S S 0,25đ 1 2 -- HẾT---