Đề thi HSG Toán 9 năm 2019 – 2020 phòng GD&ĐT Buôn Ma Thuột – Đắk Lắk

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi chọn học sinh giỏi môn Toán năm 2019 – 2020 phòng GD&ĐT Buôn Ma Thuột – Đắk Lắk giúp bạn ôn tập kiến thức, chuẩn bị tốt kì thi sắp tới. Mời bạn đọc đón xem.

23 12 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 9

Môn: Toán 9

Thông tin:

5 trang 7 tháng trước

Tác giả:

Profile Hà Việt Anh
P
HÒNG GIÁO
C
VÀ
ÀO O
T
P BUÔN MA THU T
---------
THI CH C
SINH
I THCS
C
P THÀNH
PH
C
2019-2020
MÔN: TOÁN
Th i gian: 150 phút (không tính giao )
Ngày thi: 09/01/2020
Bài 1
: (3,
0
Cho
bi
2
2
2 1 1 2020
3 1
2 1 2 1
1 1
3 3
M
x
x x
.
a)
Rút g
M
.
b) Tìm
giá tr
M
.
Bài
2
: (5,
0
a)
Ch
5 4 3 2
3 6 3 9 6P x x x x x x
không th
à
s
ng
uyên.
b)
P x
chia cho
1x 3x
Tìm
s
P x
cho
1 3x x
.
c) Tìm nghi ên c ình sau:
5 10 2x y z t xyzt
.
d) Cho
,a b
là hai s
ãn
2 2
2a b
,
hãy tìm giá tr
th
3 2 3 2M a b a b b a b a
.
Bài
3
: (4,0
Cho
hàm s
2
1y m x m
a)
Tìm
m
àm
s
ên
t
b) Tìm
m
àm
s
ành
t
c)
Tìm
m
àm
s
2
; 2 1
y
x y x
v
à
2
1y m x m
quy.
d)
Tìm
m
àm
s
à
tr
ành
m
2.
Bài 4
: (2,0
Cho hình vuông ABCD có c K AB, MF
BC (E
AB, F
Bài
5
: (6,0
Cho òn ;O
R
và
;O
r
ti
ài
t
.
Ti
ài
AD c
,A
O D O
. Ti G à
hình chi
c
a) Ch
E
H EA
;
b) Tính
A
H
theo
R
và
O
P d
;
c) Tính
theo
R
và
r
;
d) Gi
4
AD
DM cm
,
tính
R
và
r
;
e) G
1
1
;O
R
ti
ài
v
;O
R
và
;O
r
.
Ch
m
inh r
1
1
1 1
R R r
.
-
--------------- H
-
---------------
BÀI GI
B
ài 1
:
a)
Rút g
M
(
0x
)
2
2
2 2
2 1 1 2020 2 3 3 2020
3 1 3 1
4 4 4 4 4 4
2 1 2 1
1 1
3 3
2 1
1010 1 1 1010 2020 2020
1 1 1
1 1
1
1 1
M
x x
x x x x
x x
x
x x x x
x x x x
x x
x x x x
b) T
ìm giá tr
M
.
Vì
2
2
2020
0 1 1 2020
1
x x x M
x x
. D y ra
0x
V
2
020MaxM
khi
0x
B
ài 2
:
(5,0
a)
Gi
x a a Z
là nghi
ê
n c
P x
5
4 3 2
3 6 3 9 6 0P a a a a a a
+
) N
3a
thì
5
4 3 2
3 6 3 9 9; 6 9 9a a a a a P a
(mâu thu
ì
0 9P a
)
+) N
3a
thì
4
3 2 5
3 6 3 9 6 3; 3 3a a a a a P a
(mâu thu ì
0 3P a
)
V
P x
không th i à s ên.
b) Vì
P x
chia cho
1x
ê
n
1 4 1 4P x x E x P
Vì
P x
chia cho
3x
ê
n
3 14 3 14P x x F x P
Gi
1
4 5
1 3
3 3 3 14 1
P a b
a b a
P x x x Q x ax b
P a b a b b
V
P x
cho
1 3x x
là
5
1x
.
c)
Không m
1x y z t
T
a có
2 5 10 5 4 10 20 10xyzt x y z t x x
10 5 10 5 15
xyzt x x x x
(vì
1
5 5x x
)
15yzt
M
à
3
yzt ttt t
3
15 2 1; 2t t t
T
H 1:
1t
; ta có
15yz
, mà
2
2
15 3 1; 2; 3yz zz z z z z
+
) V
1
z
,
ta có:
5 2 10 2 2 5 2 5 65x y xy x y
.
Do
2 5 2 5
x y
;
6
5 65 1 13 5
.
Nên ta có:
2 5 65 35
2 5 1 3
x x
y y
ho
2 5 13 9
2 5 5 5
x x
y y
+) V
2
z
, ta có:
5 3 10 4 4 5 4 5 125x y xy x y
.
Do
2 5 2 5
x y
;
125 125 1 25 5
.
Nên ta có:
65
4 5 125
2
4 5 1 3
2
x Z
x
y
y Z
ho
15
4 5 25
2
4 5 5 5
2
x Z
x
y
y Z
+
) V
3z
,
ta có:
5 4 10 6 6 5 6 5 205x y xy x y
.
Do
2 5 2 5
x y
;
2
05 205 1 41 5
.
Nên ta có:
6 5 205 35
6 5 1 1
x x
y y
ho
23
6 5 41
3
6 5 5 5
3
x Z
x
y
y Z
T
H 2:
2t
;
ta có
2 15 7yz yz
,
mà
2
2
7 2 1; 2yz zz z z z z
M
à
2
2z t z
7 2 7 3yz y y
.
L
2 2; 3y z y
+
) V
2y
,
ta có:
40
5 6 10 16
11
x x x Z
.
+
) V
3y
,
ta có:
45
5 7 10 24
19
x x x Z
.
V ình
có nghi
; ; ; 35; 3;1;1 ; 9; 5;1;1x y z t
và các hoán v
2
4
nghi
.
d)
Áp d 0, 0
2
A B
AB A B .
Ta có:
2
2
3 2 3 2 3 2 3 2M a b a b b a b a ab a ab ab b ab
2
2 2 2
3 2 3 2 10
2 10
1 5
2 2 2 2
ab a ab ab b ab a b ab
ab
ab
(vì
2
2
2a b
)
M
2
2
2 2 1a b ab ab
.
Nên
1
5 1 5 6M ab
D
2
2
2
2
2
1
3 2
3 2
a b
a b
a b
ab a ab
ab b ab
. V
6M
axM
khi
1a
b
Bài 3:
a) Hàm s
2
0 2m m
à
m s
2 1y m x m
c à
nh t
à
nh
à
m s
2 1y m x m
5
3; 0 0 3 2 1
4
m m m
c) T
2; 2 1
y x y x
là nghi
2 3 3 1
2 1 2 1
y x x x
y x y x y
à
m s
2; 2 1y x y x
và
2 1y m x m
2 1y m x m 1;1 1 2 1 2 4 2m m m m
2 1y m x m
t à tr ành m
l
à
2 0 2
1 0 1
m m
m m
.
2 1y m x m
c
à
nh t
1
; 0
2
m
A
m
và c
tr
0; 1B m
.
2
2
2
1 4 2
1 1
2 2 1 4 1 4 2
2 2
1 4 2
OA
B
m m
m
S OA OB m m m
m
m m
2
2
2
1 7 0
1
6 7 0
7
2 9 0
1 8 0
m m
m
m m
m
m m
m VN
B
ài 4
:
Vì
ABCD là hình vuông c
2a AC a 0 2AM x x a
A
EM vuông cân t
2 2
AM x
AE ME
2
x
BE AB AE a
T à hình ch
2 2
x x
BF ME CF BC BF a
2
1
2
2 2 2 2
D
EF ABCD ADE BEF CDF
x x x x
S S S S S a a a a a
2
2
2
2
2
1 1 1 3 3
4 2 2 8 8
2 2 2 2
a a a a
x x a x
.
D
1 2
2 2 2
2 2 2
a a a AC
x x AM
Bài 5:
a)
Ch
E
H EA
;
G à
BP.
Ta có: PA = PB (PA, PB là hai ti
;
OA
= OB (bán kính)
OP
là trung tr
OP
AB
L
AB
C n
ò
n
0
90BAC
hay AC
AB.
Xét BCK:
2
BC
OB OC (bán kính (O)); OP // CK (OP // AC)
2
BK
PB PK
T
a có: AH
BC (gt); BK
BC (BK là ti
AH // BK
BCP có: EH // BP (AH // BK)
EH CE
PB CP
(h
PC
K có: EA // KP (AH // BK)
EA CE
PK CP
(h
EH EA
PB PK
mà PB = PK (cmt)
EH EA
b)
Tính
A
H
theo
R
và
O
P d
;
OBP,
0
2 2 2 2 2 2
90 2 2OBP PB OP OB d R BK PB d R
B
CK:
2
BC
OB OC
;
2
BK
PB PK
(cmt),
ình
B
CK
2
2CK OP d
B
CK:
0
90CBK
,
B
A CK
(cmt)
2 2 2
2
4 2
2
BC R R
BC AC CK AC
CK d d
B
CK: AH // BK (cmt)
2
2 2 2 2 2
2
2 2 2
2
AH AC AC BK R d R R d R
AH
BK CK CK d d d
c)
Tính
theo
R
và
r
;
T
a có: PO là phân giác
APB
(PA, PB là ti
PO’ là phân giác
DPB
(PD, PB là ti ’))
a
x
F
E
B
A
D
C
M
E
K
H
C
P
M
D
A
O
O'B
L
APB
và
DPB
k bù
0
90OPO
OPO’:
0
90OPO
(
cmt), PB
OO
’ (cmt)
2
PB OB O B Rr PB Rr
M A
D = PA + PD = 2PB =
2 Rr
.
d) Gi
4
AD D
M cm
,
tính
R
và
r
;
Ta
có
2AD Rr
2 4
4
Rr
Rr a
M MO
A: O’D // OA (cùng vuông góc v
4 1
2
4 4 2
O D MD r
R r b
OA MA R
T
2
2 4 2 ; 2 2 2r r cm R r cm
e) Ch
1
1 1
1
R R r
.
O
1
N
C
M
D
A
O
O'B
G à ti
1
O
. Áp d
Vì
AN là ti
ài
c
;O R
v
à
1 1 1
; 2O R AN RR
Vì
DN là ti
ài
c
;O r
v
à
1 1 1
; 2O
R DN rR
1 1
1
1 1 1
2 2 2AD AN DN Rr RR rR
R r R
---------------- H ----------------
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GIÁO C VÀ ÀO O THI CH C SINH I THCS TP BUÔN MA THU T C P THÀNH PH C 2019-2020 --------- MÔN: TOÁN
Th i gian: 150 phút (không tính giao ) Ngày thi: 09/01/2020 Bài 1: (3,0 2 1 1 2020 Cho bi M . 2 2 3 x 1 2 x 1 2 x 1 1 1 3 3 a) Rút g M . b) Tìm giá tr M . Bài 2: (5,0 a) Ch 5 4 3 2 P x x 3x 6x 3x 9x 6 không th à s nguyên. b)
P x chia cho x 1 x 3 Tìm s
P x cho x 1 x 3 . c) Tìm nghi ên c ình sau: 5 x y z t 10 2xyzt .
d) Cho a, b là hai s ãn 2 2 a b 2 , hãy tìm giá tr th M a 3b a 2b b 3a b 2a . Bài 3: (4,0 Cho hàm s y m 2 x m 1 a) Tìm m àm s ên t b) Tìm m àm s ành t c) Tìm m àm s y x 2; y 2x 1 và y m 2 x m 1 quy. d) Tìm m àm s à tr ành m 2. Bài 4: (2,0 Cho hình vuông ABCD có c K AB, MF BC (E AB, F Bài 5: (6,0 Cho òn ;
O R và O ; r ti ài t . Ti ài AD c A O , D O . Ti G à hình chi c a) Ch EH EA ;
b) Tính AH theo R và OP d ;
c) Tính AD theo R và r ; d) Gi AD DM
4cm , tính R và r ; e) G O ; R ti ài v ;
O R và O ; r . Ch 1 1 1 1 1 minh r . R R r 1 ---------------- H ---------------- BÀI GI Bài 1: a) Rút g M ( x 0 ) 2 1 1 2020 2 3 3 2020 M 2 2 3 x 1 3 4x 4 x 4 4x 4 x 4 x 1 2 x 1 2 x 1 1 1 3 3 1010 1 1 1010 2 x 1 2020 2020 2 2 x 1 x x 1 x x 1 x 1 x x 1 x x 1 x 1 x x x 1 b) Tìm giá tr M . 2020 Vì 2 x 0 x x 1 1 M 2020 . D y ra x 0 2 x x 1 V MaxM 2020 khi x 0 Bài 2: (5,0 a) Gi x a a Z là nghi ên c P x 5 4 3 2 P a a 3a 6a 3a 9a 6 0 +) N a 3 thì 5 4 3 2 a 3a 6a 3a 9a 9; 6 9 P a 9 (mâu thu ì P a 0 9 ) +) N a 3 thì 4 3 2 5 3a 6a 3a 9a 6 3; a 3 P a 3 (mâu thu ì P a 0 3 ) V P x không th i à s ên.
b) Vì P x chia cho x 1 ên P x x 1 E x 4 P 1 4
Vì P x chia cho x 3 ên P x x 3 F x 14 P 3 14 P 1 a b a b 4 a 5 Gi P x
x 1 x 3 Q x ax b P 3 3a b 3a b 14 b 1 V
P x cho x 1 x 3 là 5x 1 . c) Không m x y z t 1
Ta có 2xyzt 5 x y z t 10 5 4x 10 20x 10 xyzt
10x 5 10x 5x 15x (vì 1 x 5 5x ) yzt 15 Mà 3 yzt ttt t 3 t 15 t 2 t 1; 2
TH 1: t 1; ta có yz 15 , mà 2 2 yz zz z z 15 z 3 z 1; 2; 3 +) V z 1, ta có: 5 x y 2 10 2xy 2x 5 2 y 5 65 .
Do 2x 5 2y 5 ; 65 65 1 13 5 . Nên ta có: 2x 5 65 x 35 2x 5 13 x 9 ho 2 y 5 1 y 3 2 y 5 5 y 5 +) V z 2 , ta có: 5 x y 3 10 4xy 4x 5 4 y 5 125 .
Do 2x 5 2y 5 ; 125 125 1 25 5 . Nên ta có: 65 15 x Z x Z 4x 5 125 2 4x 5 25 ho 2 4 y 5 1 3 4 y 5 5 5 y Z y Z 2 2 +) V z 3 , ta có: 5 x y 4 10 6xy 6x 5 6 y 5 205 .
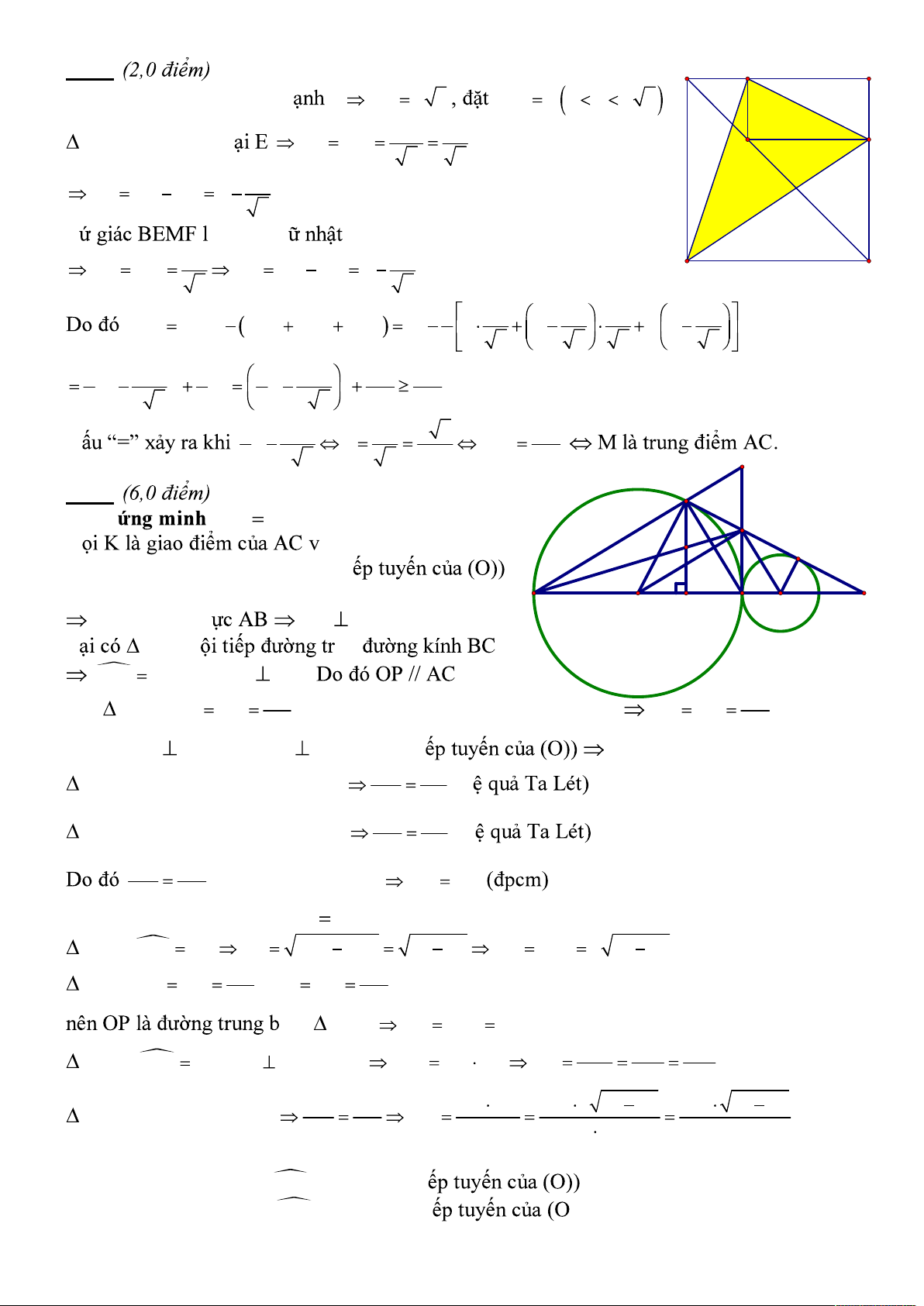
Do 2x 5 2y 5 ; 205 205 1 41 5 . Nên ta có: 23 x Z 6x 5 205 x 35 6x 5 41 ho 3 6 y 5 1 y 1 6 y 5 5 5 y Z 3 TH 2: t 2 ; ta có 2 yz 15 yz 7 , mà 2 2 yz zz z z 7 z 2 z 1; 2 Mà z t 2 z 2 yz 7 2 y 7 y 3 . L y z 2 y 2; 3 40 +) V y 2 , ta có: 5 x 6 10 16x x Z . 11 45 +) V y 3 , ta có: 5 x 7 10 24x x Z . 19 V ình có nghi ; x ; y z; t 35; 3; 1; 1 ; 9; 5;1; 1 và các hoán v 24 nghi . A B d) Áp d AB A 0, B 0 . 2 Ta có: 2 2 M a 3b a 2b b 3a b 2a 3ab a 2ab 3ab b 2ab 2 2 2 2 3ab a 2ab 3ab b 2ab a b 10ab 2 10ab 1 5ab (vì 2 2 a b 2 ) 2 2 2 2 M 2 2 2 a b 2ab 1 ab . Nên M 1 5ab 1 5 6 a b 2 2 a b 2 D a b 1 . V MaxM 6 khi a b 1 2 3ab a 2ab 2 3ab b 2ab Bài 3: a) Hàm s m 2 0 m 2 àm s y m 2 x m 1 c ành t ành 5 àm s y m 2 x m 1 3; 0 0 3 m 2 m 1 m 4 c) T y x 2; y 2x 1 là nghi y x 2 3x 3 x 1 y 2x 1 y x 2 y 1 àm s y x 2; y 2x 1 và y m 2 x m 1 y m 2 x m 1 1; 1 1 m 2 m 1 2m 4 m 2 y m 2 x m 1 t à tr ành m m 2 0 m 2 1 m là . y m 2 x m 1 c ành t A ; 0 và c m 1 0 m 1 m 2 tr B 0; m 1 . 2 1 1 m m 1 4 m 2 2 S 2 OA OB 2 m 1 4 m 1 4 m 2 OAB 2 2 m 2 m 1 4 m 2 2 m 1 m 7 0 m 6m 7 0 m 1 2 2 m 2m 9 0 m 1 8 0 VN m 7 Bài 4: A E B Vì ABCD là hình vuông c a AC a 2 AM x 0 x a 2 x AM x AEM vuông cân t AE ME F 2 2 a M x BE AB AE a 2 T à hình ch x x BF ME CF BC BF a D C 2 2 1 x x x x 2 S S S S S a a a a a DEF ABCD ADE BEF CDF 2 2 2 2 2 2 2 2 1 a 1 1 a 3a 3a 2 2 x x a x . 4 2 2 2 2 2 2 8 8 1 a a a 2 AC D x x AM 2 2 2 2 2 2 K Bài 5: A a) Ch EH EA ; P G à BP. E D
Ta có: PA = PB (PA, PB là hai ti ; OA = OB (bán kính) C O H B O' M OP là trung tr OP AB L ABC n òn 0 BAC 90 hay AC AB. BC BK Xét BCK: OB OC
(bán kính (O)); OP // CK (OP // AC) PB PK 2 2
Ta có: AH BC (gt); BK BC (BK là ti AH // BK EH CE BCP có: EH // BP (AH // BK) (h PB CP EA CE PCK có: EA // KP (AH // BK) (h PK CP EH
EA mà PB = PK (cmt) EH EA PB PK
b) Tính AH theo R và OP d ; OBP, 0 2 2 2 2 2 2 OBP 90 PB OP OB d R BK 2PB 2 d R BC BK BCK: OB OC ; PB PK (cmt), 2 2 ình BCK CK 2OP 2d 2 2 2 BC 4R 2R BCK: 0 CBK 90 , BA CK (cmt) 2 BC AC CK AC CK 2d d 2 2 2 2 2 2 AH AC AC BK 2R 2 d R 2R d R BCK: AH // BK (cmt) AH 2 BK CK CK d 2d d
c) Tính AD theo R và r ;
Ta có: PO là phân giác APB (PA, PB là ti
PO’ là phân giác DPB (PD, PB là ti ’)) L
APB và DPB k bù 0 OPO 90 OPO’: 0 OPO 90 (cmt), PB OO’ (cmt) 2 PB OB O B Rr PB Rr M
AD = PA + PD = 2PB = 2 Rr . d) Gi AD DM
4cm , tính R và r ; Ta có AD 2 Rr 2 Rr 4 Rr 4 a M
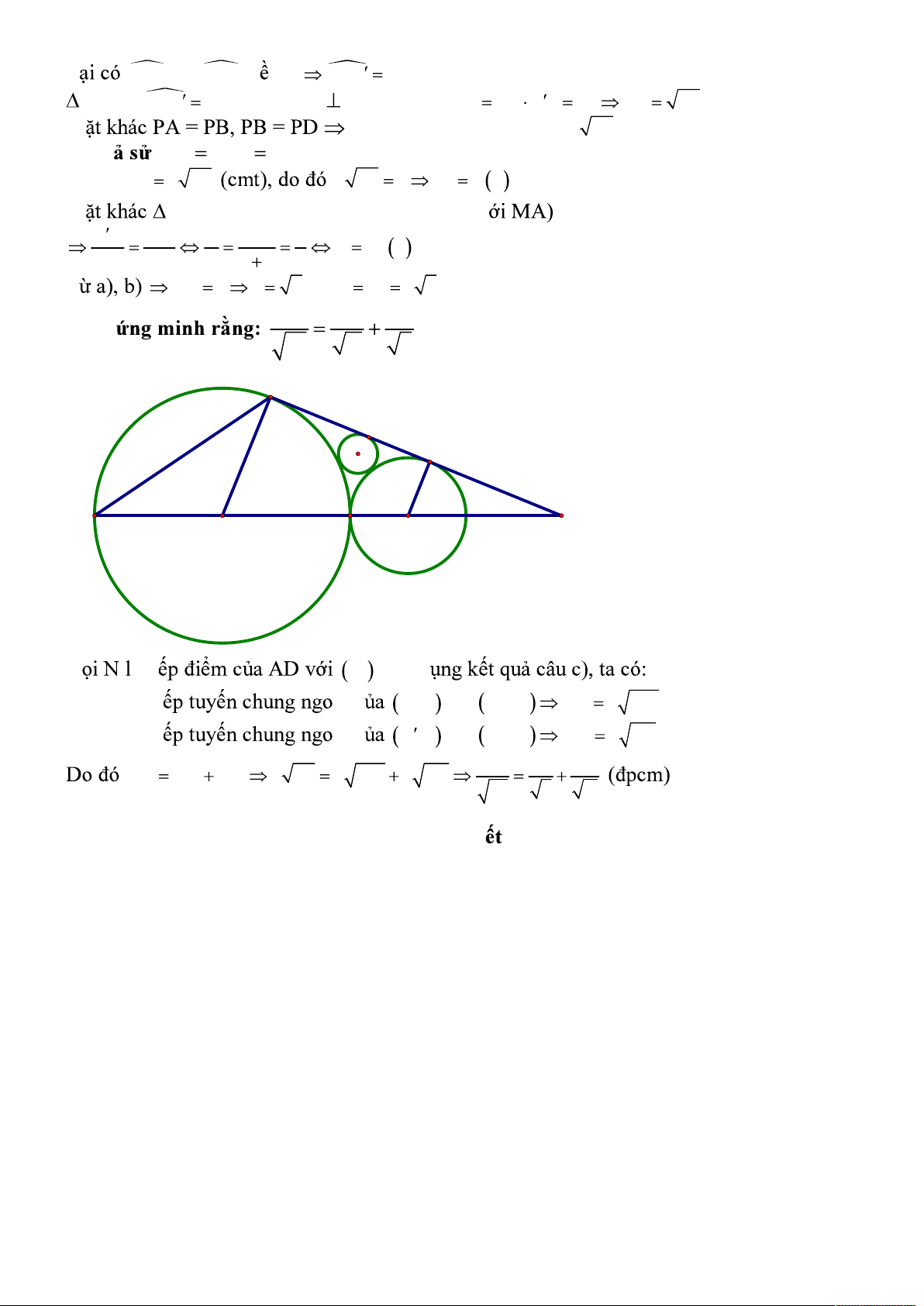
MOA: O’D // OA (cùng vuông góc v O D MD r 4 1 R 2r b OA MA R 4 4 2 T 2 2r 4 r 2 ; cm R 2r 2 2 cm 1 1 1 e) Ch . R R r 1 A N D O1 C O B O' M G à ti O . Áp d 1 Vì AN là ti ài c ;
O R và O ; R AN 2 RR 1 1 1 Vì DN là ti ài c
O ; r và O ; R DN 2 rR 1 1 1 1 1 1 AD AN DN 2 Rr 2 RR 2 rR 1 1 R r R 1 ---------------- H ----------------