Đề thi HSG Toán 9 năm 2019 – 2020 phòng GD&ĐT thị xã Sa Pa – Lào Cai

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ SA PA
LỚP 9, NĂM HỌC 2019 - 2020
Môn thi: Toán
Thời gian làm bài: 150 phút, không kể thời gian giao đề
ĐỀ THI CHÍNH THỨC
(Đề thi gồm có 01 trang,05 câu) Ngày thi: 04/01/2020 Câu 1. (2,0 điểm):
a) Tìm số tự nhiên n để A = n2012 + n2002 + 1 là số nguyên tố.
b) Tìm các số nguyên x và y thỏa mãn 2 x + 2 2
y + 2xy = y + 2 . Câu 2. (4,0 điểm): Cho biểu thức:  x + 2 1  4 = −  . x P  x x +1 x +1 3 a) Rút gọn P;
b) Tìm các giá trị của x để 8 P = ; 9
c) Tìm giá trị lớn nhất của P, giá trị nhỏ nhất của P. (  m − ) 1 x + y = 3m − 4
Câu 3. (4,0 điểm): Cho hệ phương trình với tham số m:  x +  (m − )1y = m
a) Giải và biện luận hệ phương trình theo m;
b) Tìm các giá trị nguyên của m để nghiệm của hệ phương trình là các số nguyên;
c) Tìm các giá trị của m để hệ phương trình có nghiệm dương duy nhất. Câu 4. (4,0 điểm):
4.1: Cho các số dương x, y, z thoả mãn điều kiện: xy + yz + zx = 671. Chứng minh rằng: x y z 1 + + ≥ 2 2 2
x − yz + 2013 y − zx + 2013 z − xy + 2013 x + y + z
4.2: Cho đường thẳng (d) có phương trình: 2(1− m) 2 y = .x +
(với m tham số, m ≠ 2). m − 2 m − 2
a) Tìm điểm cố định mà đường thẳng (d) luôn đi qua;
b) Xác định giá trị tham số m để khoảng cách từ gốc toạ độ O đến đường thẳng (d) là lớn nhất. Câu 5. (6,0 điểm):
Đường tròn (O) đường kính AB = 2R. Gọi M là một điểm bất kỳ thuộc đường tròn
tâm O khác A,B. Các tiếp tuyến của đường tròn tâm O tại A và M cắt nhau tại E. Vẽ MP
vuông góc với AB(P∈ AB), vẽ MQ vuông góc với AE (Q∈ AE).
a) Chứng minh rằng: bốn điểm A,E,M,O cùng thuộc một đường tròn và tứ giác APMQ là hình chữ nhật;
b) Gọi I là trung điểm của PQ. Chứng minh O,I,E thẳng hàng;
c) Gọi K là giao điểm của EB và MP. Chứng minh ∆EAO đồng dạng với ∆ MPB và K là trung điểm của MP;
d) Đặt AP = x. Tính MP theo x và R.Tìm vị trí của điểm M trên đường tròn (O) để
hình chữ nhật APMQ có diện tích lớn nhất. --------Hết--------
Cán bộ coi thi không giải thích gì thêm. PHÒNG GD&ĐT
KỲ THI CHỌN HỌC SINH GIỎI CẤP THỊ XÃ THỊ XÃ SA PA
LỚP 9, NĂM HỌC 2019 – 2020 Môn thi: Toán
HƯỚNG DẪN CHẤM CHÍNH THỨC
(Hướng dẫn chấm, thang điểm gồm có 06 trang)
A. Hướng dẫn chấm:
- Cho điểm lẻ tới 0,25 điểm.
- Tổng điểm toàn bài không làm tròn.
- Vẫn cho điểm tối đa nếu học sinh làm chính xác bằng cách khác. B. Đáp án: CÂU NỘI DUNG ĐIỂM
Xét n = 0 thì A = 1 không phải nguyên tố; n =1 thì A = 3 0,25 nguyên tố.
Xét n > 1 có A = n2012 – n2 + n2002 – n + n2 + n + 1 0,25
= n2[(n3)670 – 1] + n.[(n3)667 – 1] + (n2 + n + 1)
1.a) Mà [(n3)670 – 1] chia hết cho n3 - 1, suy ra (n3)670 – 1 chia hết (1 đ) cho n2 + n + 1 0,25
Tương tự: (n3)667 – 1 chia hết cho n2 + n + 1
Do đó A chia hết cho n2 + n + 1 > 1 nên A là hợp số khi n > 1 0,25 Câu 1
Vậy số tự nhiên cần tìm n = 1. (2 đ) Ta có: 2 2
x + 2y + 2xy = y + 2 ⇔ (x + y)2 2 = −y + y + 2 0,25 ⇔ (x + y)2 = (1+ y)(2 − y) Do ( + )2 x y ≥ 0 x,
∀ y nên (1+ y)(2 − y) ≥ 0 ⇔ 1 − ≤ y ≤ 2 . 1.b) Suy ra y∈{ 1; − 0; 1; } 2 0,25
(1 đ) Với y = 1
− , PT trở thành x2 − 2x +1 = 0 ⇔ x = 1∈ Z
Với y = 0 , PT trở thành x2 − 2 = 0 ⇒ x ∉ Z 0,25
Với y =1, PT trở thành x2 + 2x −1 = 0 ⇒ x ∉ Z
Với y = 2 , PT trở thành x2 + 4x + 4 = 0 ⇔ x = −2∈ Z .
Vậy có 2 cặp (x; y) thỏa mãn đề bài (1;− ) 1 ;( 2 − ;2). 0,25
T×m ®­îc §K: x ≥ 0 0,25  x + 2 1  4 x  − . 0,25
( x +1)(x − x +1) x +1 3 Câu 2 2.a) (4 đ) (2 đ)
 x + 2 − (x − x +1)  4 = x  .
( x +1)(x − x + 0,5  1) 3  x +1 4 = . x
( x +1)(x − x +1) 3 0,5 1 4 0,25 = x 3(x − x +1) 0,25 Vậy P 4 = x với x ≥ 0 3(x − x +1)
b) Với x ≥ 0 ta được P 4 = x . Ta có 3(x − x +1)
P = 8 ⇔ 2x −5 x + 2 = 0 (TM§K) 0,25 2.b) 9
(1 đ) Giải PT 2x −5 x + 2 = 0 ra được 1 0,5
x = 4; x = (TM§K) 1 2 4 Vậy 1
x = 4; x = thỏa mãn đề bài. 0,25 1 2 4
* Víi x ≥ 0; 3(x − x +1) > 0 ⇒ P ≥ 0 , min P = 0 khi x = 0 0,25 4 * Víi x > 0 thì P = 1 3( x + −1) 0,25 x 1 2.c)
Theo bất đẳng thức Cô-si có 1 x + ≥ 2 nªn x + −1≥1. x x (1 đ) 4 0,25 Do ®ã P ≤ . 3 4
DÊu “=” x¶y ra khi x = 1. Do đó maxP = khi x = 1 0,25 3 Vậy 4
maxP = khi x = 1; min P = 0 khi x = 0. 3 (  m − ) 1 x + y = 3m − 4 ( ) 1 a)  x +  (m − )1y = m (2)
Rút y từ (1) rồi thay vào (2) và rút gọn 0,5
được m(m − 2)x = (m − 2)(3m − 2) 0,25
Với m ≠ 0, m ≠ 2 hệ có một nghiệm duy nhất 0,25  3m − 2 m − 2 ;   m m    0,25 Câu 3 3
Với m = 0, hệ vô nghiệm 0,25 (4,0 đ) (4,0
Với m = 2, hệ vô số nghiệm: (x; 2 – x) với x ∈ R 0,5
đ) b) Với m = 1 thì nghiệm là (1; -1). 0,25
Với m = - 1 thì nghiệm là (5; 3) 0,25
Với m = - 2 thì nghiệm là (4; 2). 0,25
Với m = 2 thì nghiệm là (x; 2 – x) với x ∈ Z. 0,25
c) Với m ≠ 0, m ≠ 2 hệ có một nghiệm duy nhất 0,25  3m − 2 m − 2 ;   m m    Ta thấy 2 3m − 2 m − 2 x = = + 2 = y + 2 m m 0,25
Từ đó y > 0 thì x > 0 0,25 m − 2 y =
> 0 ⇒ m < 0 hoặc m > 2. m 0,25
Vậy m < 0 hoặc m > 2 thỏa mãn đề bài.
Trước tiên ta chứng minh bất đẳng thức: Với ∀ a, b, c ∈ R và a b c
(a +b + c)2 2 2 2 x, y, z > 0 ta có + + ≥ (*) x y z x + y + z 0,25
Dấu “=” xảy ra ⇔ a b c = = x y z
Thật vậy, với a, b ∈ R và x, y > 0 ta có a b (a +b)2 2 2 + ≥ (**) x y x + y ⇔ ( 2 2
a y + b x)(x + y) ≥ xy(a + b)2
⇔ (bx − ay)2 ≥ 0 (luôn đúng)
Áp dụng bất đẳng thức (*) ta có x y z VT = + + 2 2 2
x − yz + 2013 y − zx + 2013 z − xy + 2013 2 2 2 x y z 0,25 = + + 4.1 x( 2 x − yz +
) y( 2y − zx+ ) z( 2 2013 2013 z − xy + 2013) (2 đ) 2 0,25 Câu 4
(x + y + z) VT ≥ (1) (4,0 đ) 3 3 3
x + y + z − 3xyz + 2013(x + y + z)
Theo đề bài xy + yz + zx = 671 nên x( 2
x − yz + 2013) = x( 2
x + xy + zx +1342) > 0 , tương tự 0,25 y ( 2
y − zx + 2013) > 0, z( 2
z − xy + 2013) > 0 Mà 3 3 3
x + y + z − xyz = (x + y + z)( 2 2 2 3
x + y + z − xy − yz − zx) 0,25
= (x + y + z) (x + y + z)2 − 3(xy + yz + zx)   (2)
= (x + y + z)(x + y + z)2 −3.671+ 2013   = ( + + )3 x y z (3) 0,25 Từ (1) và (3) ta suy ra
(x + y + z)2 1 VT ≥ = ( 0,25
x + y + z)3 x + y + z 0,25
Dấu “=” xảy ra ⇔ x = y = z = 2013 . 3 − m 4.2 (d) : 2(1 ) 2 y = .x +
; với m tham số, m ≠1; m ≠ 2 m − 2 m − 2 (2 đ)
Gọi (x ; y ) là điểm cố định (d) luôn đi qua. Thay vào PT của 0 0 3 (d) ta có: 0,25 2(1− m) 2 y = .x + , Với mọi m 0 0 m − 2 m − 2
⇔ my − 2y = 2x − 2mx + 2 , m ∀ 0 0 0 0
⇔ m(y + 2x ) − 2y − 2x − 2 = 0;∀m 0,25 0 0 0 0 y + 2x = 0 x =1 0 0 0 ⇔  ⇔ 2y 2x 2 0  − − − = y =  2 −  0,25 0 0 0
Vậy điểm cố định mà đường thẳng (d) luôn đi qua là (1; - 2)
b) Nhận thấy (d) không đi qua O
Tìm được tọa độ giao điểm A của đồ thị hàm số với trục Ox: A 1 0,25 ;0   m 1  − 
Giao điểm B của đồ thị hàm số với trục Oy: B 2 0;    m 2  −  0,25
Ta có: ∆ AOB vuông tại O và có khoảng cách từ O đến (d) là OH (đường cao) nên: 1 1 1 = + Hay 2 2 2 OH OA OB 2 1 1 1 1 2 (m − 2) = + ⇔ = (m −1) + 2 2 2 2 OH x y OH A B 4 2 4 2 ⇔ OH = ⇔ OH = 0,25 2 2 2
4(m −1) + (m − 2) 5m −12m + 8 2 2 ⇔ OH = ≤ = 5 ; Dấu “=” xẩy ra 6 x = . 5 0,25 2 6 2 4 4 5(m − ) + 5 5 5
Xét m =1⇒ y = 2
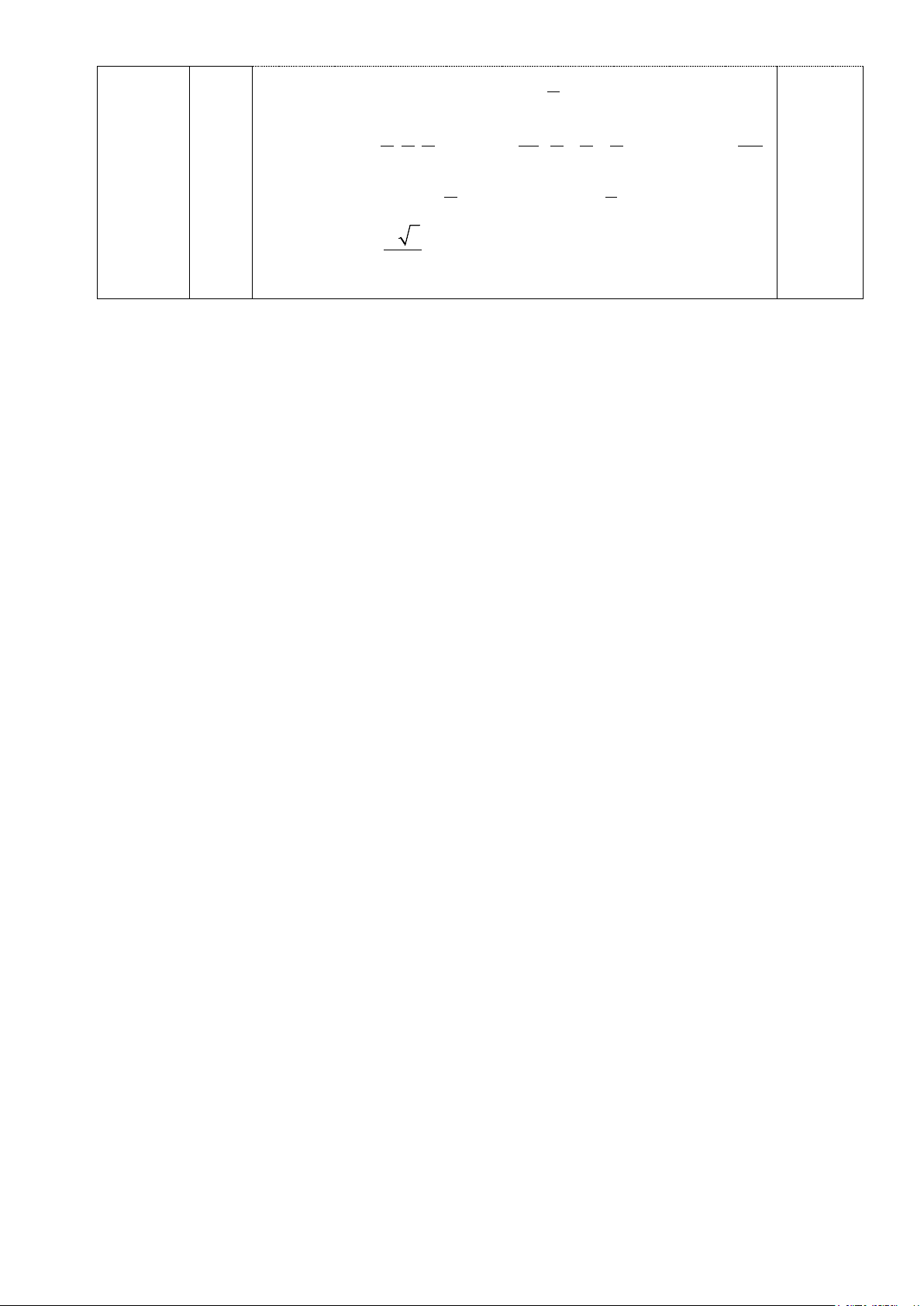
− ; K/c từ O đến (d) bằng 2 0,25 Vậy 6 OH = khi x m 5 = ax 5 Câu 5 5 (6 đ) I M Q E 4 K I B A O P x 0,25
a) Vì AE là tiếp tuyến của đường tròn (O) tại A ⇒ AE⊥ AO
⇒ ∆OEA vuông ở A ⇒O, E, A ∈ đường tròn đường kính OE 0,25 (1)
Vì ME là tiếp tuyến của đường tròn (O) tại M ⇒ ME ⊥ MO
⇒ ∆MOE vuông ở M ⇒ M, O, E ∈ đường tròn đường kính 0,25 OE (2)
Từ (1) và (2) ⇒ Bốn điểm A, M, O, E cùng thuộc một đường 0,25 tròn * Tứ giác APMQ có  0,25 =  =  o EAO APM PMQ = 90 0,25
=> Tứ giác APMQ là hình chữ nhật
b) Ta có I là giao điểm của 2 đường chéo AM và PQ của hình 0,25 chữ nhật APMQ
nên I là trung điểm của AM. (3) 0,25
Mà E là giao điểm của 2 tiếp tuyến tại M và tại A. Dễ chứng
minh được OE là đường trung trực của đoạn thẳng AM. (4) 0,25
Từ (3) và (4) suy ra: O, I, E thẳng hàng. 0,25
c) Hai tam giác AEO và PMB đồng dạng vì chúng là 2 tam giác vuông và  = 
AOE ABM (so le trong của OE // BM). 0,5 => AO AE = (5) BP MP 0,25
Mặt khác, vì KP//AE, nên ta có tỉ số KP BP = (6) 0,25 AE AB
Từ (5) và (6) ta có : AO.MP = AE.BP = KP.AB mà AB = 2.OA => MP = 2.KP 0,25
Vậy K là trung điểm của MP. 0,25
d) Ta dễ dàng chứng minh được : 4 abcd  a + b + c + d  ≤ 
(*) (theo bất đẳng thức Cô-si) 4    0,25
Dấu “=” xảy ra khi và chỉ khi a = b = c = d 0,25 0,25 MP = 2 2 2 2 2
MO − OP = R − (x − R) = 2Rx − x Ta có: S = S 0,25 APMQ = 2 3
MP.AP = x 2Rx − x = (2R − x)x S đạt max ⇔ 3
(2R − x)x đạt max ⇔ x.x.x(2R – x) đạt max 0,25 ⇔ x x x . . (2R − x) đạt max 3 3 3 5
Áp dụng (*) với a = b = c = x , 3 4 4 Ta có : x x x 1  x x x  R . . (2R − x) ≤ + + +  (2R − x) = 4 3 3 3 4 3 3 3    16 0,25
Do đó S đạt max ⇔ x = (2R − x) ⇔ 3 x = R . 3 2 0,25
Vậy khi MP = R 3 thì hình chữ nhật APMQ có diện tích lớn 2 0,25 nhất. --------Hết-------- 6
Document Outline

• TOAN 9-CHINH THUC
• TOAN9-HDC CHINH THUC