Đề Thi HSG Toán 9 Sở GD Bến Tre 2025-2026 Có Lời Giải Chi Tiết

SỞ GD&ĐT BẾN TRE
ĐỀ THI CHỌN HỌC SINH GIỎI ĐỀ CHÍNH THỨC MÔN: TOÁN LỚP 9
Thời gian làm bài: 150 phút (không kể thời gian giao đề) Câu 1. (5,0 điểm).
a) Tính giá trị biểu thức: A = 4 + 15 + 4 − 15 − 2 3 − 5 .
x − 5 + 2 x + 6 x + 9
b) Rút gọn biểu thức: B =
(x  0) và tìm x sao cho 2022 B = . x + 3 x + 2 2023 2 2 x + y 85
Câu 2. (3,0 điểm). Tìm tất cả các cặp số nguyên ( ; x y) thỏa = . x + y 13 2 2 2  x − 2   x + 2   x − 4 
Câu 3. (3,0 điểm). Giải phương trình: 9 + −10       = 0 . 2  x +1   x −1  x −1  
Câu 4. (3,0 điểm). Cho a,b,c là các số thực không âm. Chứng minh rằng 2 2 2 2 2 2 2
a 3a + 6b + b 3b + 6c + c 3c + 6a  (a + b + c) .
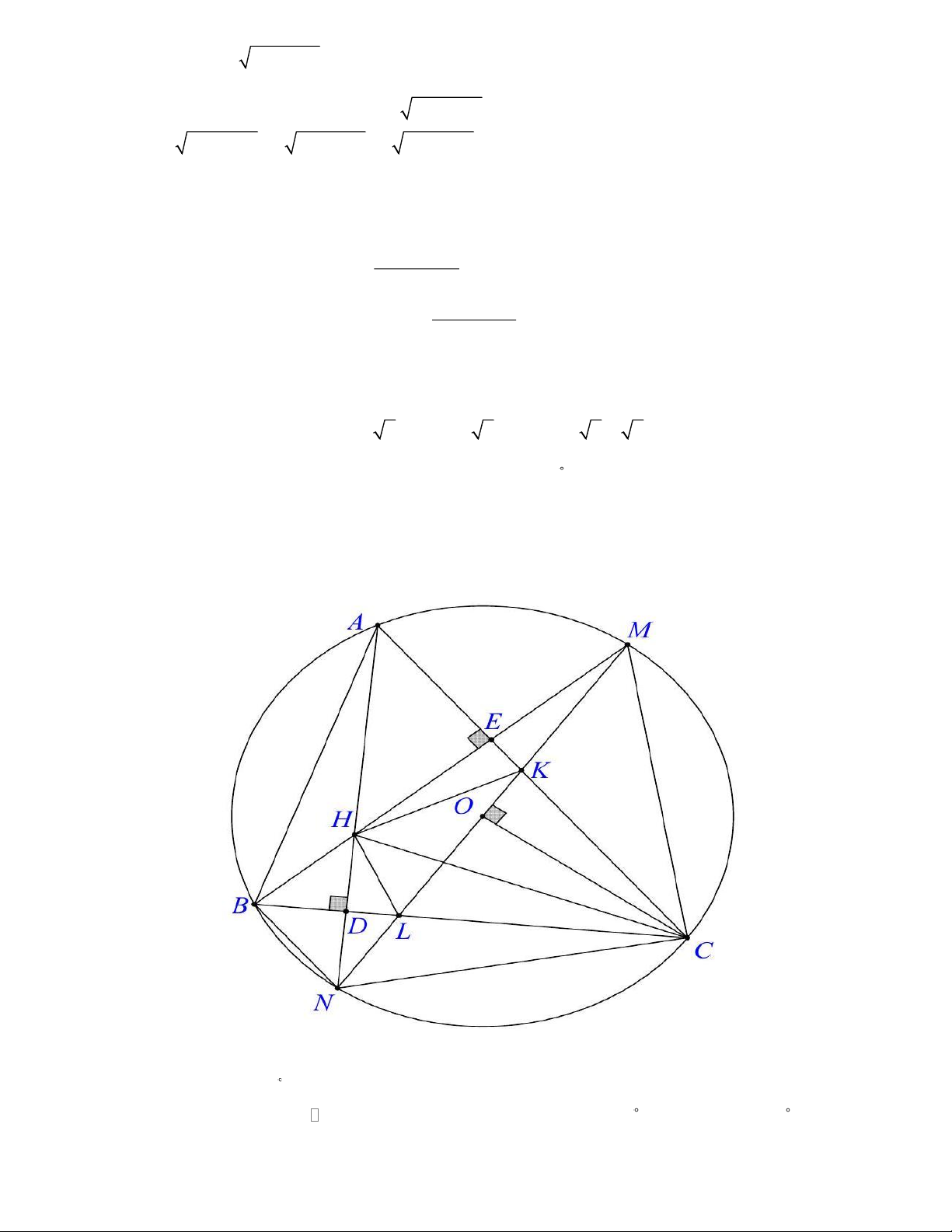
Câu 5. (3,0 điểm). Cho tam giác ABC có ACB = 45 , gọi O là tâm đường tròn
ngoại tiếp và H là trực tâm của tam giác ABC . Đường thẳng qua O và vuông góc
với CO cắt AC và BC lần lượt tại điểm K và L . Chứng minh chu vi của tam
giác HKL bằng với đường kính của (O) .
Câu 6. (3,0 điểm). Cho hai đường tròn (O và (O tiếp xúc ngoài nhau tại điểm 2 ) 1 )
T . Hai đường tròn này nằm trong đường tròn (O và tiếp xúc với (O lần lượt 3 ) 3 )
tại điểm M (M (O và điểm N ( N (O ). Tiếp tuyến chung tại T của (O 1 ) 2 ) 1 ))
và (O cắt O tại điểm P(P và O nằm cùng phía của đường thẳng MN) . Đường 2 ) 3 3
thẳng PM cắt (O tại A( A  M ) , đường thẳng PN cắt O tại D(D  N ) và 1 ) 2
đường thẳng MN cắt (O và O lần lượt tại B(B  M ) và C (C  N ) . Gọi E là 1 ) 2
giao điểm của AB và CD .
a) Tứ giác AEDP là hình gì? Giải thích.
b) Chứng minh rằng: EBC = EDA . ---HẾT--- LỜI GIẢI: Câu 1. (5,0 điểm).
a) Tính giá trị biểu thức: A = 4 + 15 + 4 − 15 − 2 3 − 5 .
x − 5 + 2 x + 6 x + 9
b) Rút gọn biểu thức: B =
(x  0) và tìm x sao cho 2022 B = . x + 3 x + 2 2023 Lời giải 8 + 2 15 8 − 2 15
a) A = 4 + 15 + 4 − 15 − 2 3 − 5 = + − 2  6 − 2 5 2 2 Trang 1 5 + 3 + 5 − 3 = − 2 ( 5 − ) 1 = 2 2
b) Với x  0 , khi đó ta có: 2
x − 5 + 2 x + 3 x − 5 + 2
x − 5 + 2 x + 6 x + 9
x − 5 + 2 ( x + 3) ( x +3) B = = = = x + 3 x + 2 x + 3 x + 2 x + 3 x + 2 x + 3 x + 2 2 x + 2 x +1 ( x +1) x +1 = = = x + x + ( x + )1( x +2) . 3 2 x + 2 2022 x +1 2022 B =  =
 2023 x + 2023 = 2022 x + 4044 2023 x + 2 2023  x = 2021 2
 x = 2021  x = 4084441 (nhan). + Vậy, với x x  0 thì 1 B = và 2022 B = tại x = 4084441. x + 2 2023 2 2 x + y 85
Câu 2. (3,0 điểm). Tìm tất cả các cặp số nguyên ( ; x y) thỏa = . x + y 13 Lời giải
Vì x, y  Z nên 2 2
x + y  Z; x + y  Z 2 2 x + y 85 517  x + y 2 2 ( ) Ta có : =  x + y = x + y 13 13
Vì 5.17 không chia hết 13 nên 2 2
x + y  Z khi ( x + y) 13
 x + y = 13k (k Z)
 y = 13k − x Thay (2) vào (1) ta có: 2 x + ( 2
13k − x ) = 85k 2 2
 2x − 26kx +169k − 85k = 0 Ta có 2  = k − ( 2 Δ (13 )
2 169k − 85k ) = k (170 −169k ) Để (*) có nghiệm thì Δ  0
 k (170 −169k )  0 170 1  0  k  = 1+ 169 169  k = 1 x + y =13
Với k = 1 ta có hệ phương trình  2 2 x + y = 85
Giải hệ phương trình này, ta được x = 6; y = 7 hoặc x = 7; y = 6 . Vậy các cặp số ( ;
x y) thoả mãn là x = 6; y = 7 hoặc x = 7; y = 6 Trang 2 2 2 2  −   +   − 
Câu 3. (3,0 điểm). Giải phương trình: x 2 x 2 x 4 9 + −10       = 0 . 2  x +1   x −1  x −1   Lời giải ĐK : x  1  2 2 2  x − 2   x + 2   x − 4  9 + −10       = 0 2  x +1   x −1  x −1   2 2  x − 2 
x − 2 x + 2  x + 2   9 −10  + = 0      x +1 
x +1 x −1  x −1  − + Đặt x 2 x 2 = ; a
= b . Ta có phương trình: x +1 x −1 2 2
9a −10ab + b = 0  ( 2
9a − 9ab) − ( 2 ab − b ) = 0 
9a (a − b) − b(a − b) = 0 
( a −b)(9a −b) = 0  a − b = 0   9a − b = 0
+) Nếu a − b = 0 thì: x − 2 x + 2 − = 0 x +1 x −1
 ( x − 2)( x − )
1 − ( x + 2)( x + ) 1 = 0 2 2
 x − 3x + 2 − x − 3x − 2 = 0  6 − x = 0
 x = 0 (thoa mãn).
+) Nếu 9a − b = 0 thì: x − 2 x + 2 9. − = 0 x +1 x −1
 9( x − 2)( x − )
1 − ( x + 2)( x + ) 1 = 0 2 2
 9x − 27x +18 − x − 3x − 2 = 0 2
 8x − 30x − 25 = 0 15 + 5 17 15 − 5 17  x = (thoa mãn) ; x = (thoa mãn) 1 1 8 8 
Vậy phương trình đã cho có 3 nghiệm là: 15 5 17 x = ; x = 0 . 1,2 3 8
Câu 4. (3,0 điểm). Cho a,b,c là các số thực không âm. Chứng minh rằng 2 2 2 2 2 2 2
a 3a + 6b + b 3b + 6c + c 3c + 6a  (a + b + c) . Lòi giải Cách 1. Với a, , b c  0 Ta có: 2 2 2 2 2 2 2 2 2
3a + 6b = 2a − 4ab + 2b + a + 4ab + 4b = 2(a − b) + (a + 2b)  (a + 2b) 2
vì (a − b)  0, a  ,b 2 2 2
 a 3a + 6b  a (a + 2b) = a (a + 2b) 2 = a + 2ab Trang 3 Tương tự: 2 2 2
b 3b + 6c  b + 2bc 2 2 2
c 3c + 6a  c + 2ca 2 2 2 2 2 2 2 2 2 2
 a 3a + 6b + b 3b + 6c + c 3c + 6a  a + 2ab + b + 2bc + c + 2ca = (a + b + c)
Dấu "=" xảy ra khi và chỉ khi a = b = c Cách 2. 2 + + Áp dụng BĐT: (x y z) 2 2 2
x + y + z  3 + + Ta có: a b b
3a + 6b = 3(a + b + b ) 2 ( ) 2 2 2 2 2 2  3 = (a + 2b) 3 Cách 3. Áp dụng ( 2 2 m + n )( 2 2 x + y ) 2 BĐT :
 (mx + ny) Ta có:
a + b = (a + b ) = ( 2 2 2 2 2 2 + )( 2 2 a + b ) 2 2 3 6 3 2 1 2 (
2)  (1.a + 2 b 2) = (a + 2b)
Câu 5. (3,0 điểm). Cho tam giác ABC có ACB = 45 , gọi O là tâm đường tròn
ngoại tiếp và H là trực tâm của tam giác ABC . Đường thẳng qua O và vuông góc
với CO cắt AC và BC lần lượt tại điểm K và L . Chứng minh chu vi của tam
giác HKL bằng với đường kính của (O) . Lời giải
Đường thẳng vuông góc với CO cắt đường tròn (O) tại hai điểm M , N . Ta có
CAN = CMN = 45 (tam giác OMC vuông cân).
Do AH ⊥ BC suy ra CAD là tam giác vuông cân ( ABC = 45 ) suy ra CAD = 45 .
Từ đó suy ra CAN = CAH nên ,
A H , N thẳng hàng. Trang 4
Gọi AD và BE là hai đường cao của tam giác ABC .
Ta có tứ giác ABDE nội tiếp (hai đỉnh D và E kề nhau cùng nhìn cạnh AB dưới cùng một góc 90 )
 CAN = HBC mà CAN = CBN suy ra HBC = NBC
Xét BHN có BD vừa là đường cao vừa là phân giác nên BHN cân tại B
 BD là đường trung trực của HN .
Do L thuộc BD nên LH = LN . Chứng minh tương tự ta có KH = KM .
Như vậy chu vi tam giác HKL là HL + KL + HK = NL + LK + KM = MN là đường kính của (O).
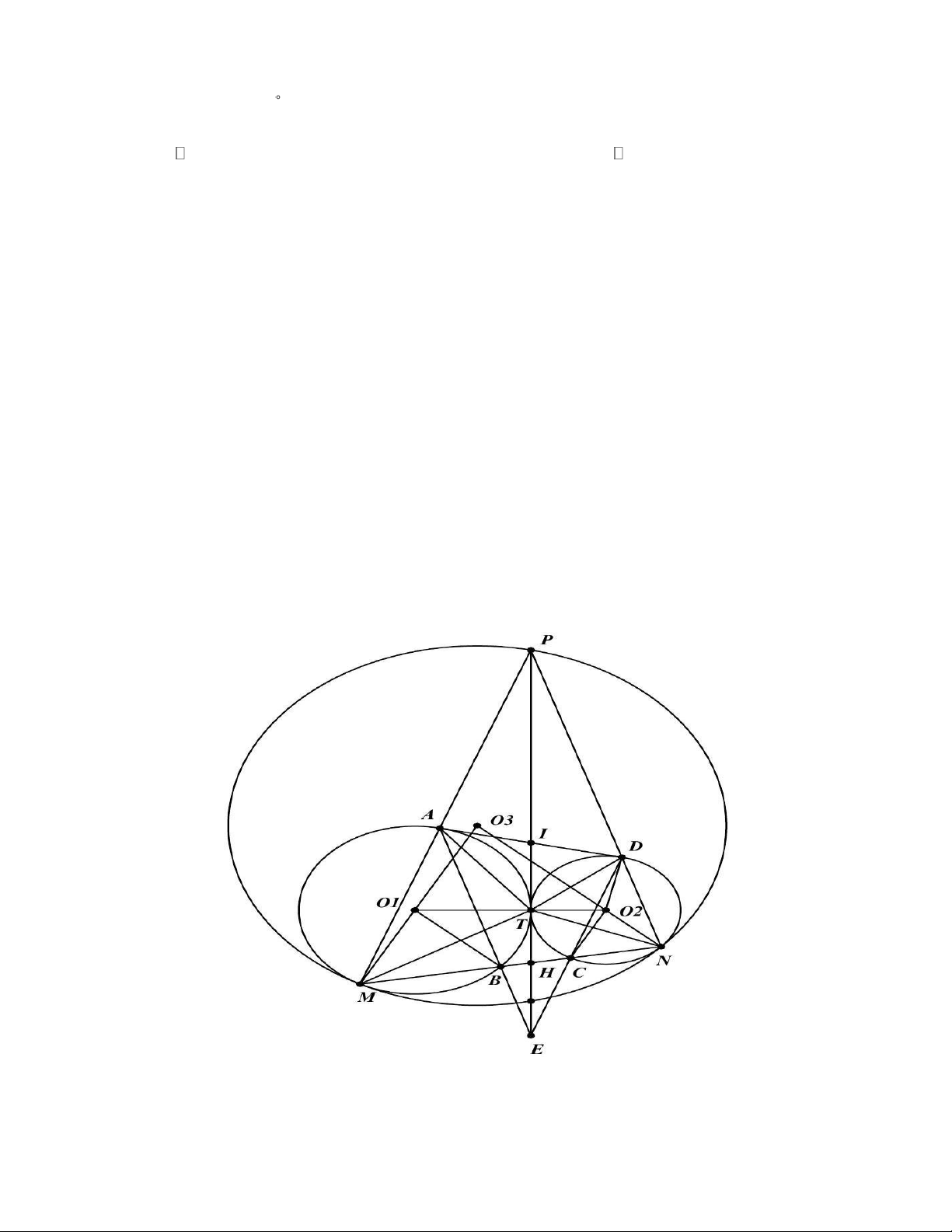
Câu 6. (3,0 điểm). Cho hai đường tròn (O và (O tiếp xúc ngoài nhau tại điểm 2 ) 1 )
T . Hai đường tròn này nằm trong đường tròn (O và tiếp xúc với (O lần lượt 3 ) 3 )
tại điểm M (M (O và điểm N (N (O ). Tiếp tuyến chung tại T của (O và 1 ) 2 ) 1 ))
(O cắt O tại điểm P ( P và O nằm cùng phía của đường thẳng MN). Đường 2 ) 3 3
thẳng PM cắt (O tại A( A  M ) , đường thẳng PN cắt O tại D(D  N ) và 1 ) 2
đường thẳng MN cắt (O và O lần lượt tại B(B  M ) và C (C  N ) . Gọi E là 1 ) 2
giao điểm của AB và CD .
a) Tứ giác AEDP là hình gì? Giải thích. b) Chứng minh rằng: EBC = EDA . Lời giải
a) Tứ giác AEDP là hình gì? Giải thích.
Ta có (O tiếp xúc trong với (O tại M  O ,O , M thẳng hàng; 3 ) 1 ) 1 3
Ta có (O tiếp xúc trong với (O tại N  O ,O , N thẳng hàng; 3 ) 2 ) 1 3
ΔMO B,ΔMO N là các tam giác cân có ˆ
M chung nên MO B = MO N ; 1 3 1 3
ΔNO C,ΔNO M là các tam giác cân có ˆ
N chung nên NO C = NO M ; 2 3 2 3 Trang 5 Lại có : 1 1 MAB = MO ;
B MPN = MO N (các góc nội tiếp và góc ở tâm cùng chắn 1 3 2 2 một cung)
 MAB = MPN  AE / /PD( có cặp góc đồng vị bằng nhau) ; 1 1
NDC = NO C; NPM = NO M (các góc nội tiếp và góc ở tâm cùng chắn một 2 3 2 2 cung)
 NDC = NPM  DE / /PA (có cặp góc đồng vị bằng nhau)
Tứ giác AEDP có các cạnh đối song song nên là hình bình hành.
b) Chứng minh rằng: EBC = EDA .
Ta có PT là tiếp tuyến của (O ) 2
 PT = PA PM ; 1
PT là tiếp tuyến của (O ) 2
 PT = PD  PN ; 2   =  ( 2 = ) PA PN PA PM PD PN PT  = ( ) 1 PD PM
Gọi H là giao điểm của PE và MN , vì BE / /PN;CE / / AM nên theo hệ quả của định lý Ta-let, ta có : BE EH CE EB PN = =  = (  
2) Từ (1) và (2), ta có : EB PA PN = =   , mà PN HP PM EC PM EC PD  PM 
AEDP là hình bình hành EB ED  PA = E ; D PD = EA  = ; EC EA
Xét EBC và EDA có : ˆ E chung ; EB ED = (chứng minh trên); EC EA
 EBC  EDA( .
c g.c)  EBC = EDA. Trang 6