-
Thông tin
-
Hỏi đáp
Đề Thi Khảo Sát Chất Lượng Năm 2024 Sở Giáo Dục Và Đào Tạo Sở Hải Dương | Học viện Hành chính Quốc gia
Hàm số nào dưới đây có đồ thị như hình vẽ sau? Cho hình trụ T có chiều cao gấp đôi bán kính đáy và thể tích bằng 16pi. Tính diện tích toàn phần của hình trụ đó Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Lịch sử nhà nước và pháp luật (NAPA) 62 tài liệu
Học viện Hành chính Quốc gia 766 tài liệu
Đề Thi Khảo Sát Chất Lượng Năm 2024 Sở Giáo Dục Và Đào Tạo Sở Hải Dương | Học viện Hành chính Quốc gia
Hàm số nào dưới đây có đồ thị như hình vẽ sau? Cho hình trụ T có chiều cao gấp đôi bán kính đáy và thể tích bằng 16pi. Tính diện tích toàn phần của hình trụ đó Tài liệu giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời đọc đón xem!
Môn: Lịch sử nhà nước và pháp luật (NAPA) 62 tài liệu
Trường: Học viện Hành chính Quốc gia 766 tài liệu
Thông tin:
Tác giả:
Preview text:
lOMoARcPSD|498 307 39 y y
Câu 2: Số phức liên hợp của số phức z i 1 2i có iểm biểu diễn là iểm nào dưới ây? A. H 1;2 B. F 2;1 C. G 1;2 D. E 2; 1
Câu 3: Cho hai hàm số f x , g x liên tục trên oạn a b; và số thực k tùy ý. Trong các khẳng ịnh sau, khẳng ịnh nào sai? b b b b A. f x dx f x dx . B. f kx dx k f x dx . a a a a b b b b b C. kf x dx k f x dx . D. f x g x dx f x dx g x dx a a a a a
Câu 4: Cho hình chóp S ABC. có áy là tam giác ều cạnh bằng a , cạnh bên SA vuông góc với mặt phẳng áy và
SA a 2 . Thể dch của khối chóp S ABC. bằng 2a33 6a3 6a3 A. . B. 2a . C. . D. . 312 4
Câu 5: Cho mặt cầu S : x2 y2 z2 2x 4y 2z 3 0 . Tính bán kính R của mặt cầu S . A. R 3 . B. R 3. C. R 3 3 . D. R 9. 1
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39
Câu 6: Cho hàm số y f x có bảng biến thiên như sau: x 1 3 f 0 0 x 3 f x 2
Hàm số ạt cực ại tại A. x 1. B. x 3. C. x 2. D. x 2. y
Câu 7: Hàm số nào dưới ây có ồ thị như hình vẽ sau? A. y x 2x 1 4 2x2 1. B. y . x 1 C. y x3 3x2 1. D. y x4 2x2 1. Câu 8: Cho hàm số y
2x2 1 . Mệnh ề nào dưới ây úng?
A. Hàm số nghịch biến trên khoảng 0;
B. Hàm số nghịch biến trên khoảng 1;1
C. Hàm số ồng biến trên khoảng ;0
D. Hàm số ồng biến trên khoảng 0;
Câu 9: Cho số phức z thỏa mãn z 2z 6 2i. Điểm biểu diễn số phức z có tọa ộ là A. 2; 2 B. 2;2 C. 2; 2 D. 2;2
Câu 10: Cho hai số phức z1 1 2i z; 2 3 4i . Tìm phần ảo của số phức w 2z1 3z2 . A. 6 . B. 8 . C. 5 . D. 3 .
Câu 11: Cho hàm số y f x có bảng biến thiên: x 1 3 f 0 0 x 2
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39 2 f x 2
Hàm số ã cho ồng biến trên khoảng A. 3; B. 1;3 C. ; 1 D. 2;2
Câu 12: Đồ thị hàm số y 2x 1 có {ệm cận ngang là x 3 A. y 3 B. y C. y 2 D. y
Câu 13: Trong không gian Oxyz , cho các iểm A 1;0;2 , B 1;2;1 , C 3;2;0 và D 1;1;3 . Đường thẳng i
qua A và vuông góc với mặt phẳng BCD có phương trình là x 2 t x 1 t x 1 t x 1 t A. y 4 4t . B. y 2 4t . C. y 4 . D. y 4t . z 4 2t z 2 2t z 2 2t z 2 2t
Câu 14: Cho hàm số f x có ạo hàm f x x2 x
x 2 2 2x 4 , x . Số iểm cực trị của hàm số f x là A. 4 B. 1 C. 2 D. 3
Câu 15: Diện dch xung quanh của hình nón có bán kính áy là R và ường sinh bằng l là A. 2 Rl . B. Rl C. Rl . D. Rl .
Câu 16: Cho cos3xdx F x C . Khẳng ịnh nào dưới ây úng? A. F x 3sin3x . B. F x sin3x . C. F x cos3x . D. F x 3sin3x . 3
Câu 17: Giả sử a b, là các số thực dương tùy ý thỏa mãn a b2 3 256 . Mệnh ề nào sau ây úng? 3
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39
A. 2log2a 3log2b 4. B. 2log2a 3log2b 4 . C. 2log2a 3log2b 8. D. 2log2a 3log2b 8.
Câu 18: Cho hình trụ T có chiều cao gấp ôi bán kính áy và thể dch bằng 16 . Tính diện dch toàn phần của hình trụ ó. A. 24 . B. 16 . C. 8 . D. 32 .
Câu 19: Với a b, là các số thực dương tùy ý và a 1,log 1 bằng 1a b3 A. 3logab . B. 3logab . C. logab. D. logab.
Câu 20: Tìm tập nghiệm S của phương trình 2x 1 8. A. S 1 . B. S 4 . C. S 1 . D. S 2 .
Câu 21: Cho hình lăng trụ ứng ABCD A B C D. có áy ABCD là hình vuông cạnh a AA, 2a . Thể dch của
khối lăng trụ ã cho bằng 2 3 3 4a3 3 A. a . B. 4a . C. . D. 2a . 3 3 x 1 y 2 z
Câu 22: Trong không gian với hệ trục tọa ộ Oxyz , cho ường thẳng d : . Điểm nào dưới ây 2 1 2 thuộc ường thẳng d ? A. M 1;1;2 . B. M 1; 2; 0 . C. M 3;3;2 . D. M 2;1; 2 .
Câu 23: Từ các chữ số 1;2;3;4;5;6;7;8;9 có thể lập ược bao nhiêu số tự nhiên có 3 chữ số ôi một khác nhau. A. A 3 3 9 B. 39 C. 93 D. C9
Câu 24: Trong không gian với hệ trục tọa ộ Oxyz , cho iểm A 3; 1; 1 . Gọi A là hình chiếu của A lên trục Oy . Tính ộ dài oạn OA . A. OA 2 . B. OA 1. C. OA 10 . D. OA 11 .
Câu 25: Cho biết số phức liên hợp của số phức z là z 3 i . Số phức z là 4
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39 A. z 3 i . B. z 3 i . C. z 1 3i . D. z 1. 3 i
Câu 26: Cho hình hộp chữ nhật ABCD A B C D có AB a BC, 2a và AA 3a . Khoảng cách giữa hai
ường thẳng BD và A C bằng A. 2a. B. 2a. C. a . D. 3a .
Câu 27: Cho hình chóp ều S ABCD.
có AB 2a SA, a 5 . Góc giữa hai mặt phẳng SAB và ABCD bằng A. 45 B. 60 C. 75 D. 30
Câu 28: Trong không gian với hệ tọa ộ Oxyz , viết phương trình mặt phẳng qua iểm M 2; 3; 4 và nhận
2;4;1 làm vectơ pháp tuyến. n A. 2x 4y z 10 0. B.2x 4y z 12 0. C. 2x 4y z 12 0. D. 2x 4y z 11 0. 2 2 2
Câu 29: Cho f x dx 3 và g x dx 1. Giá trị f x 5g x x dx bằng 0 0 0 A. 10 . B. 8 . C. 12 . D. 0 .
Câu 30: Trong không gian Oxyz , có tất cả bao nhiêu giá trị nguyên của tham số m ể x2 y2
z2 2 m 2 x 2 m 1 z 3m2 5 0 là phương trình của một mặt cầu? A. 4 . B. 6 . C. 7 . D. 5 .
Câu 31: Hàm số nào sau ây ồng biến trên tập xác ịnh của nó? A. y 13 x . B. y e x. C. y log x. D. y lnx.
Câu 32: Giá trị lớn nhất của hàm số y x3 12x 2 trên oạn 3;0 bằng A. 16 . B. 18 . C. 2 . D. 11 .
Câu 33: Tìm tập nghiệm S của bất phương trình log 1 2x 0. A. S 0; 13 . B. S 0; 12 . C. S 0; . D. S ; 12 . 5
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39
Câu 34: Cho cấp số nhân un có u2 3;u3 9 . Công bội q của cấp số nhân ã cho bằng A. 3 . B. 2 . C. . D. . Câu 35: x2024dx bằng A. x2023 C . B. 2024x2023 C . C. x2025 C . D. x2025 C .
Câu 36: Trong một lớp học có hai tổ. Tổ 1 gồm 8 học sinh nam và 7 học sinh nữ. Tổ 2 gồm 5 học sinh nam và 7
học sinh nữ. Chọn ngẫu nhiên mỗi tổ hai em học sinh. Xác suất ể trong bốn em ược chọn có 2 nam và 2 nứ bằng A. B. C. D.
Câu 37: Cho f x là hàm số liên tục trên oạn 1;2 . Biết F x là một nguyên hàm của f x trên 1;2 thỏa 2
mãn F 1 2 và F 2 4. Khi ó f x dx bằng 1 A. -6 . B. 2 . C. 6 . D. -2 .
Câu 38: Tập xác ịnh của hàm số y log0,2 4 x2 là A. 4;4 . B. 1;1 . C. 2;2 . D. 2;2 .
Câu 39: Cho hình lăng trụ ABC A B C. có áy ABC là tam giác vuông tại A AB, a AC, a 3 . Hình chiếu vuông
góc của ỉnh A lên ABC trùng với tâm của ường tròn ngoại {ếp của tam giác ABC . Trên cạnh AC lấy
iểm M sao cho CM 2MA. Biết khoảng cách giữa hai ường thẳng AM và BC bằng a
. Tính thể dch V của khối lăng trụ ã cho. 2 A. V 3a 2a 3 a 3 3 . B. V 3 . C. V a3 . D. V 3 . 2 3 2
Câu 40: Cho hai số phức z w,
thỏa mãn z 2w 3, 2z 3w 5 và z 3w 4 . Tính giá trị của biểu thức P z.w z.w A. 1 . B. 2 . C. 3 . D. 4 . 6
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39
Câu 41: Cho các số thực dương a b, khác 1 thỏa mãn log2a log 16b và ab 64 . Giá trị của biểu thức log2 ab 2 bằng A. 20 . B. . C. 32 . D. 25 .
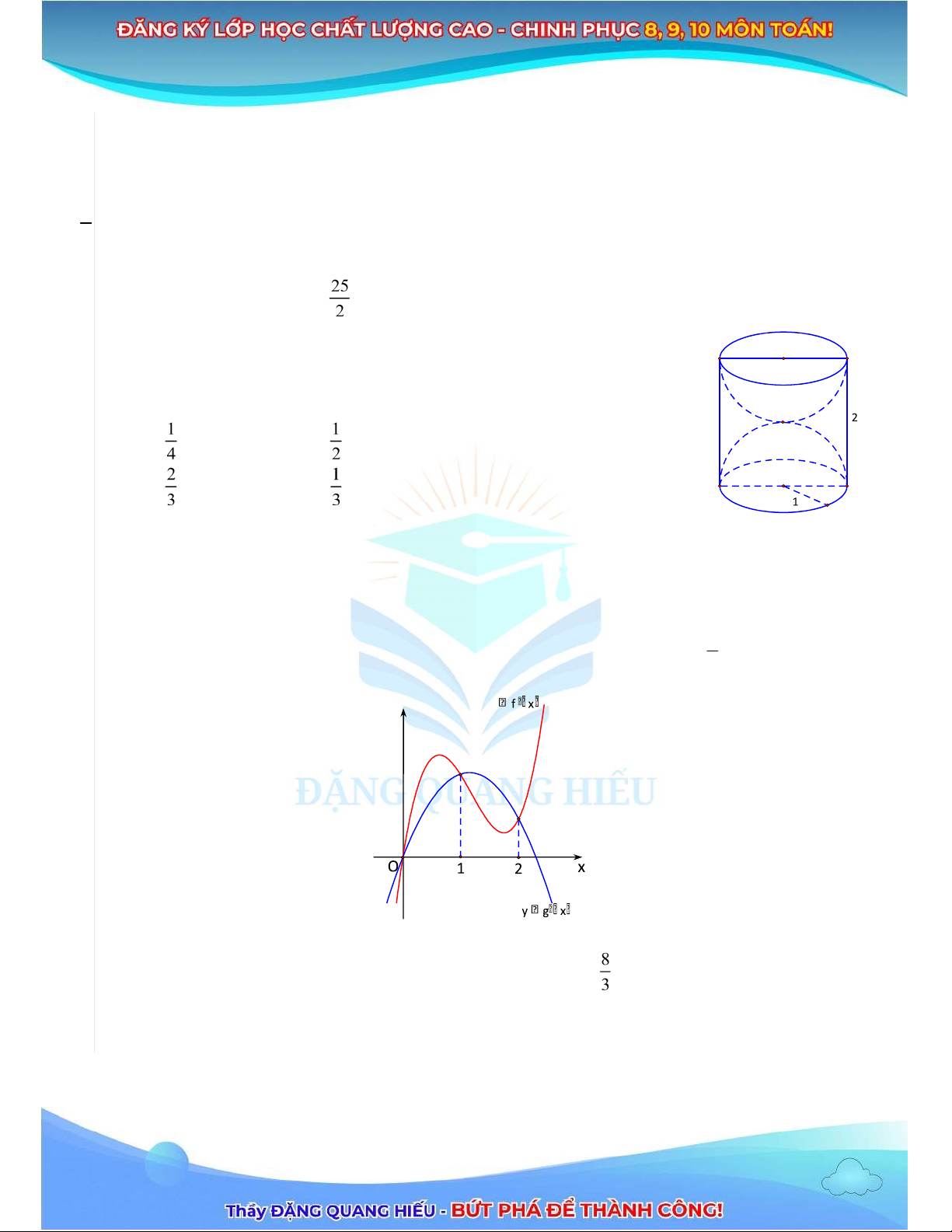
Câu 42: Một khối gỗ hình trụ tròn xoay có bán kính áy bằng 1, chiều cao bằng 2. Người
ta khoét từ hai ầu khối gỗ hai nửa khối cầu mà ường tròn áy của khối gồ là
ường tròn lớn của mỗi nửa khối cầu. Tỉ số thể dch phần còn lại của khối gỗ và cả khối gỗ ban ầu là A. . B. . C. . D. . Câu
43: Cho hai hàm số f x và g x liên tục trên và hàm số
f x ax3 bx2 cx d g, x qx2 nx p với a q, 0 có ồ thị như hình vẽ. Biết diện dch hình
phẳng giới hạn bởi hai ồ thị hàm số y f x và y g x bằng 10 và f 2 g 2 . Biết diện
dch hình phẳng giới hạn bởi hai ồ thị hàm số y f x và y g x bằng a (với a b, và a b,
nguyên b tố cùng nhau). Tính a b. y y A. 13 . B. 18 . C. 19 . D. 20 .
Câu 44: Có bao nhiêu giá trị nguyên dương của tham số m ể hàm số y x3 2lnx mx ồng biến trên khoảng 0;1 ? 7
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39 A. 6 . B. 7 . C. 5 . D. Vô số.
Câu 45: Trong không gian với hệ tọa ộ Oxyz , cho mặt cầu S : x 1 2 y 2 2 z 3 2 25 và hình nón
H có ỉnh A 3;2; 2 và nhận AI làm trục của hình nón, với I là tâm mặt cầu. Một ường sinh của
hình nón H cắt mặt cầu tại hai iểm M N, sao cho AM 3AN . Viết phương trình mặt cầu ồng tâm
với mặt cầu S và {ếp xúc với các ường sinh của hình nón H . A. x 1 2 y 2 2 z 3 2 . B. x 1 2 y 2 2 z 3 2 . C. x 1 2 y 2 2 z 3 2 . D. x 1 2 y 2 2 z 3 2 .
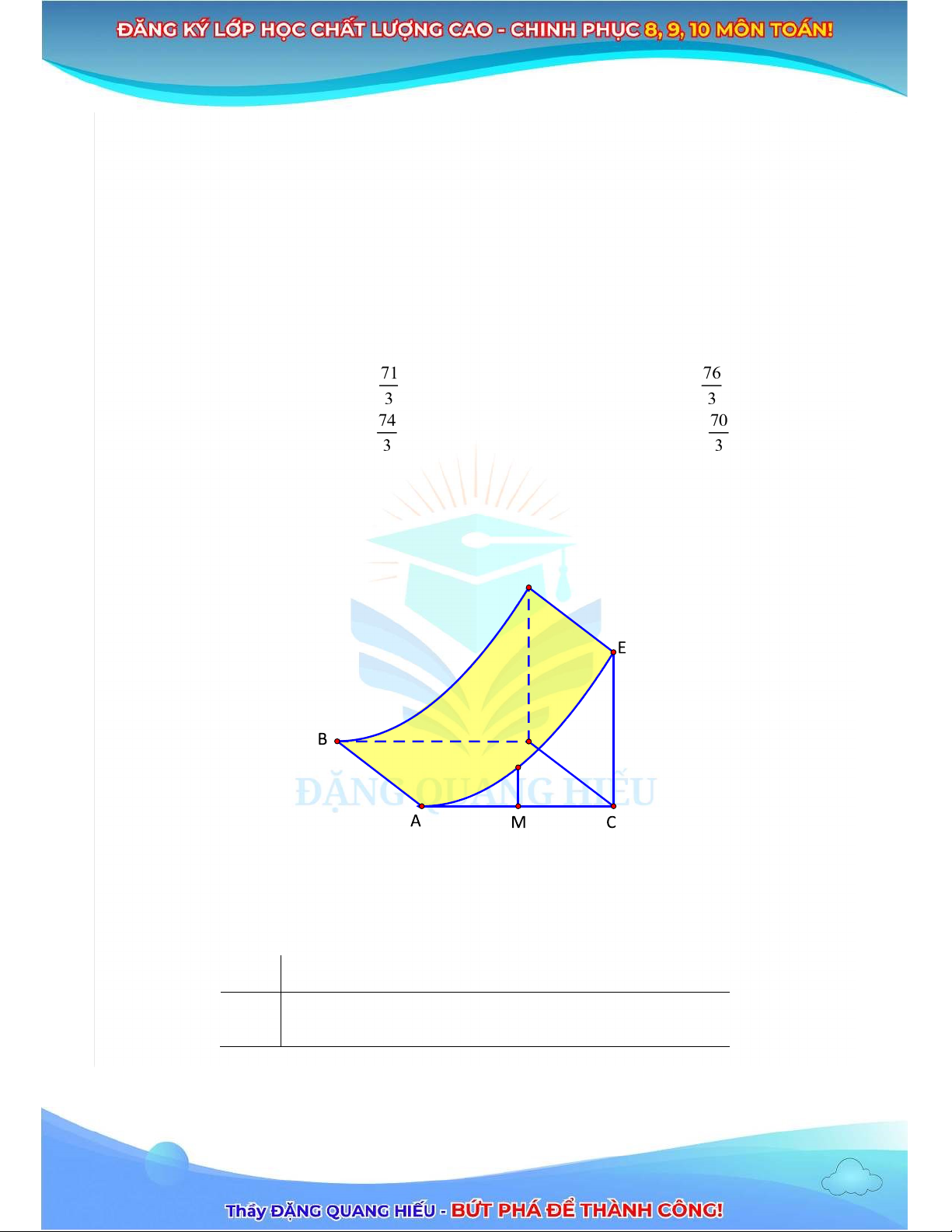
Câu 46: Chướng ngại vật "tường cong" trong một sân thi ấu X là một khối bê tông có chiều cao từ mặt ất lên
là 3 m . Giao của mặt tường cong và mặt ất là oạn thẳng AB 2 m . Thiết diện của khối tuờng cong cắt
bởi mặt phẳng vuông góc với AB tại A là một hình tam giác vuông cong ACE với AC 4m , CE 3m và
cạnh cong AE nằm trên một ường Parabol có trục ối xứng vuông góc với mặt ất. Tại vị trí M là trung
iểm của AC thì tường cong có ộ cao 1m.
Thể dch bê tông cần sử dụng ể tạo nên khối tường cong ó gần nhất với số nào dưới ây? A. 9,3m3 . B. 10m3 . C. 9,5m3 . D. 10,5m3 .
Câu 47: Cho hàm số y f x liên tục trên và có bảng biến thiên dưới ây x 1 0 2 f 0 0 0 x 8
Downloaded by ncc ncc (nnc1@gmail.com) lOMoARcPSD|498 307 39 f x 3 2 4
Có bao nhiêu giá trị nguyên của tham số m ể hàm số y f 6x 5 2024 m có 4 iểm cực {ểu? A. 5 . B. 7 . C. 6 . D. 4 .
Câu 48: Trong không gian với hệ tọa ộ Oxyz , cho hình nón N có ỉnh O 0;0;0 , có ộ dài ường sinh là
4 2 và ường tròn áy nằm trên mặt phẳng P : x 2y 2z 12 0 . Gọi C là giao tuyến của mặt
xung quanh của N với mặt phẳng Q : x z 4 0 và M là một iểm di ộng trên ường cong
C . Giá trị nhỏ nhất của ộ dài oạn thẳng OM thuộc khoảng nào dưới ây. A. 52;3 . B. 3; 72 . C. 32;2 . D. 2; 52 .
Câu 49: Cho a b c, , là các số thực thỏa mãn iều kiện a 1,b 0,c 0 và bất phương trình ax2.(b 4 )c 2 3x 1
có tập nghiệm là . Biết rằng biểu thức T 16a 1 1 ạt giá trị nhỏ nhất tại a m b, n c, p . Khi 3 b c ó, tổng m n p bằng A. . B. . C. . D. .
Câu 50: Giả sử z z1, 2 là hai trong các số phức z thỏa mãn z 1i 2 và z1 z2 z1 z2 . Khi biểu thức
P z1 2z2 ạt giá trị nhỏ nhất thì số phức z1 có dch phần thực và phần ảo bằng A. . B. . C. . D. 0 . 9
Downloaded by ncc ncc (nnc1@gmail.com)