Đề thi mẫu giữa kỳ môn Đại số tuyến tính có hướng dẫn giải

lOMoARcPSD| 36782889
Câu 1: Cho tham số 𝑚 và hệ phương trình tuyến tính sau 𝑥1 + 𝑥2 − 𝑥3 =3 {4𝑥1 +3𝑥2 −2𝑥3 + 𝑚𝑥4 =7
6𝑥1 +4𝑥2 −2𝑥3 +(𝑚+1)𝑥4 =11
a) Giải hệ phương trình khi 𝑚=2.
b) Tìm iều kiện của 𝑚 ể hệ phương trình vô nghiệm.
Hướng dẫn: a)
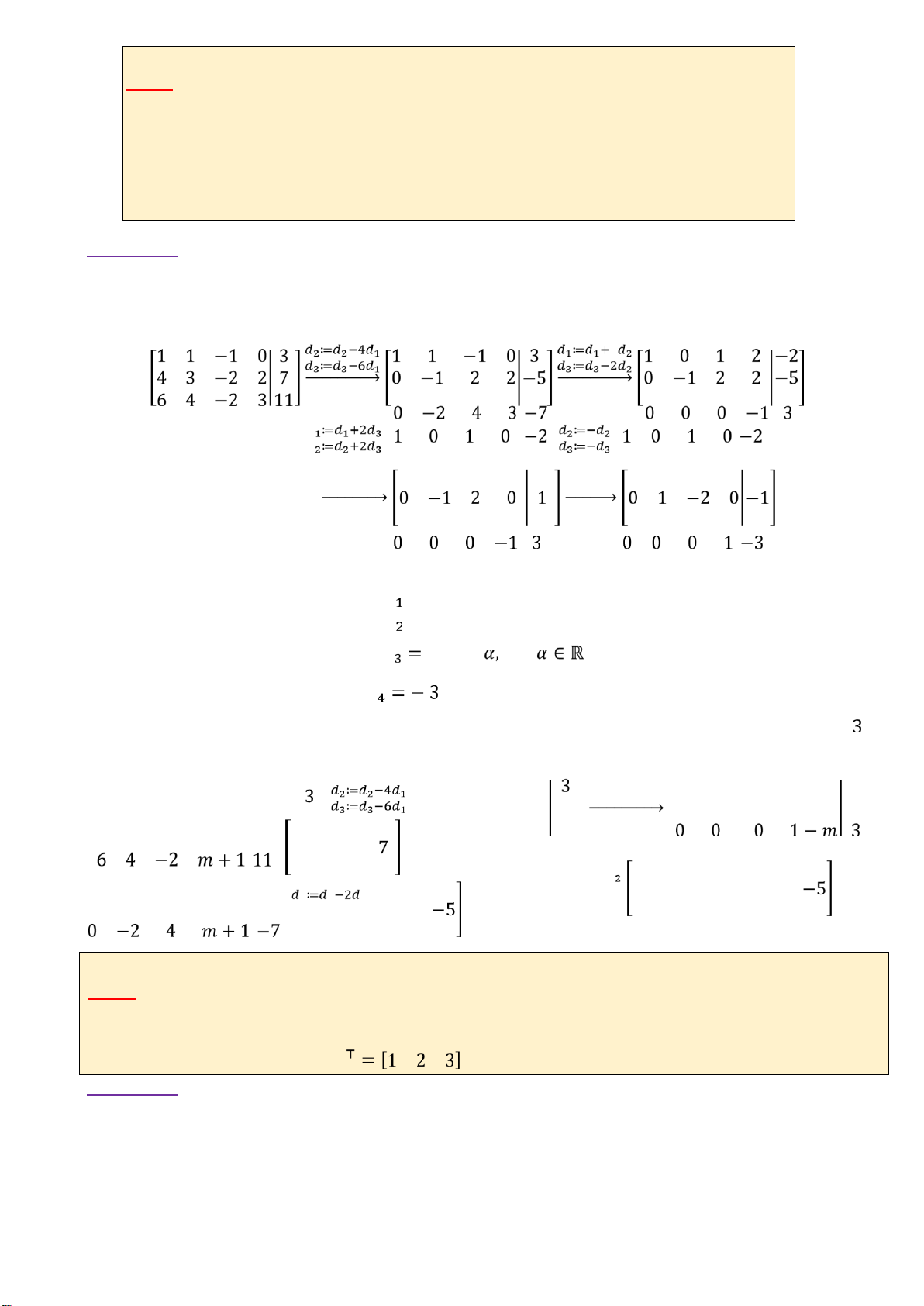
Với 𝑚=2. Áp dụng Gauss-Jordan ta có 𝑑 𝑑 → Vậy ta có Hệ phương trình vô nghiệm thì 𝑥 = 4− 𝛼 𝑥 =−1+2𝛼 1−𝑚=0 { 𝑥 ⇒𝑚 =1 𝑥 Vậy với 𝑚=1 thì hệ b) phương trình vô nghiệm. Áp dụng Gauss ta có 1 1 −1 0 1 1 −1 0 1 1 −1 0 4 3 −2 𝑚 | → &[0 −1 2 𝑚 0 −1 2 𝑚 2 1 2
Câu 2: Cho ma trận 𝐴=[1 1 1]. 1 3 0
a) Chứng tỏ 𝐴 khả nghịch và tìm ma trận nghịch ảo của 𝐴.
b) Tìm ma trận 𝑋 thỏa iều kiện 𝑋𝐴 . Hướng dẫn: a)
Cách 1: Dùng biến ổi sơ cấp lOMoARcPSD| 36782889 𝑑 → 𝑑 →
Vậy ma trận 𝐴 khả nghịch và 3 −6 1 𝐴−1 =[−1 2 0] −2 5 −1
Cách 2: Dùng ịnh thức Ta có det𝐴=| Vậy
. Nên ma trận 𝐴 khả nghịch.
Xét ma trận phụ hợp của 𝐴 bằng cách tìm các giá trị 𝑐𝑖𝑗 như sau 𝑐𝑖𝑗 𝑖+𝑗 det𝐴 𝑐
|=−3 𝑐23 =(−1)2+3 |2 1|=−5 1 3 𝑐
|=1 𝑐31 =(−1)3+1 |1 21 1|=−1 ⇒𝑐 |=2 𝑐32 =(−1)3+2 |2 2|=0 1 1 𝑐 |=6 𝑐33 =(−1)3+3 |2 1|=1 1 1 𝑐 ⇒𝐶=[ ⇒adj lOMoARcPSD| 36782889 ⇒𝐴 b) 𝑋𝐴 ⇒𝑋𝐴 ⇒𝑋 = ⇒𝑋 = ⇒𝑋 = ⇒𝑋 = 1112 2322
Câu 3 : Tìm giá tr ị c ủ a 𝑚 ể ma tr ậ n 𝐵=[ ] không kh ả ngh ị ch. 2441 345 𝑚 Hướng dẫn: Ta có 1 1 1 2 det𝐵=| | 3 4 5 𝑚 0 1 2 𝑚−6 |=|| 1 2 𝑚−6 1 2 𝑚−6 (𝑚−6)
Để ma trận không khả nghịch thì det𝐵 =0 ⇒2𝑚−10=0 ⇒𝑚 =5
Câu 4: Cho hai ma trận 𝐶=[1 1 2] và 𝐷=[𝑚 1 3]. Tìm giá trị của 𝑚 ể 𝐶 tương ương dòng 1 2 2 1 0 2 với 𝐷. Hướng dẫn: Ta có lOMoARcPSD| 36782889 𝐶=[
Để 𝐷 là ma trận tương ương dòng của 𝐶 thì 𝑚=
Câu 5: Cho 𝐴 là một ma trận thỏa iều kiện 𝐴⊤𝐴=𝐴. Chứng minh rằng 𝐴 là ma trận ối xứng và 𝐴3 =𝐴. Hướng dẫn: Ta có
𝐴⊤ =(𝐴⊤𝐴)⊤ =𝐴⊤(𝐴⊤)⊤ =𝐴⊤𝐴=𝐴
Vậy 𝐴 là ma trận ối xứng. Vậy suy ra 𝐴⊤𝐴 =𝐴 ⇒𝐴∙𝐴=𝐴 ⇒𝐴2 =𝐴 Ta lại có
VT =𝐴3 =𝐴2 ∙𝐴=𝐴∙𝐴=𝐴2 =𝐴= VP ( pcm)