



Preview text:
PHÒNG GDĐT THANH OAI
KỲ THI OLYMPIC LỚP 6, 7, 8 Năm học 2023 - 2024 ĐỀ CHÍNH THỨC
Môn: Toán – Lớp: 7
Ngày thi: 02 tháng 4 năm 2024
Thời gian làm bài: 120 phút
(Đề thi gồm 01 trang) Câu 1. (5 điểm)
1. Tính giá trị biểu thức sau:
a) A (1.2 2.3 3.4 ... 19.20)( 169 2)( 169 3)( 169 4)...( 169 20) 15 9 20 9 5.4 .9 4.3 .8 b) B 10 19 29 6 5.2 .6 7.2 .27 x y z
2. Tìm ba số x, y, z thỏa mãn: và 2 2 x 2 2 y 3 2 z 1 00 . 3 4 5 Câu 2. (4 điểm)
1. Có hai chiếc hộp giống nhau. Trong mỗi hộp chứa 4 chiếc thẻ cùng loại, mỗi thẻ
được ghi một trong các số 1, 2, 3, 4 (hai thẻ khác nhau thì ghi hai số khác nhau). Rút
ngẫu nhiên một thẻ ở trong mỗi hộp. Tính xác suất để rút được hai thẻ ghi số giống
nhau trong cùng một lần rút? 2023
2. Cho các số x, y thỏa mãn 2024 x 3 (3y 1) 0 .
Tính giá trị của biểu thức 2 2
M 2x y 9xy Câu 3. (4 điểm)
1. Tìm số nguyên x, y biết 2xy 3 x y
2. Cho x, y, z là các số nguyên thỏa mãn 2 2 2
x y z 2xyz . Chứng minh xyz24 Câu 4. (6 điểm)
Cho tam giác ABC vuông tại A có AB = AC, có D là trung điểm BC. Trên đoạn
BD lấy E (khác B, D), trên tia đối của tia CB lấy điểm F sao cho BE = CF. Kẻ các
đường thẳng vuông góc với BC tại E cắt AB tại G, đường vuông góc với BC tại F cắt
AC tại H. Gọi giao điểm của GH với BC là I
a) Chứng minh BG = CH, IG = IH
b) Kẻ đường thẳng vuông góc với CA tại C, cắt AD tại M. Chứng minh MI vuông góc với GH
c) Đường thẳng vuông góc với DG tại D cắt AC tại K, chứng minh rằng: AK + AG ≤ DG + DK
Câu 5. (1 điểm) Tìm số tự nhiên m, n sao cho 2n 3m
4 là số chính phương - Hết -
Cán bộ coi thi không giải thích gì thêm. Học sinh không sử dụng máy tính.
Họ và tên: ……………………………………………………. Số báo danh: …………
Học sinh Trường THCS: ………………………………………………………………
HƯỚNG DẪN CHẤM MÔN TOÁN 7 Câu Nội dung Điểm 1
1. Do 169 13 0 nên A = 0 1 1 15 9 9 5. 1 2 2 . 2 3 2 20 2 .3 . 3 15 9 20 9 2 5.4 .9 4.3 .8 2. B 10 19 29 6 6 5.2 .6 7.2 .27 5.2 .2.319 10 29 7.2 . 3 3 2 29 18 2 .3 2 30 18 29 20 5.2 3 5.2 .3 2 .3 1 1 . 29 19 29 18 29 18 5.2 .3 7.2 .3 2 .3 5.3 7 8 x y z 3. Từ ta suy ra: 3 4 5 2 2 2 x y z 2 2 x 2 2 y 3 2 z 2 2 x 2 2 y 3 2 z 100 4 0,5 9 16 25 18 32 75 25 25 2 x 36 2 y 64 2 z 100 0,5 x 6 Suy ra: y 8
( Vì x, y, z cùng dấu) x 10 2 x 6 0,5 y 8 z 1 0
KL: Có hai bộ (x; y; z) thỏa mãn là : (6; 8 ;10) và (-6; -8;-10) 0,5 2
1. Có tất cả 4.4= 16 khả năng xảy ra. 0,5 1,5
Gọi A là biến cố: “Rút được hai thẻ ghi số giống nhau trong cùng 1 lần rút”
Các khả năng để biến cố A xảy ra là: 1-1, 2-2, 3-3, 4-4 : có 4 khả 0,5 năng 4 1
Xác suất để biến cố A xảy ra là: 16 4 0,5 2023 2024
2. Theo đề bài: x 3 (3y 1) 0
Vì |x – 3|2023 0; (3y – 1) 2024 0 với mọi x, y nên
|x – 3|2023 + (3y – 1) 2024 0 với mọi x, y. 0.5 2,5 2023 Mà theo đề bài: 2024 x 3 (3y 1) 0
Suy ra |x – 3|2023 + (3y – 1) 2024 = 0 0,5 1
Hay: x - 3 = 0 và 3y – 1 = 0 suy ra x = 3, y = . Khi đó tính 1 3 được: 2 2
M 2x y 9xy 9 . 0,5 3 1.
2xy 3 x y 2
Biến đổi được thành: (2x 1)(2 y 1) 5 1
Lập luận tìm được (x;y) là (0;3); (-1;-2); (2;1); (-3;0) 1 2. 2 2 2
x y z 2xyz
Giả sử xyz không chia hết cho 3 suy ra x, y, z đều không chia 0,5 hết cho 3, do đó 2 2 2
x , y , z đều chia 3 dư 1, nên 2 2 2
x y z 3, từ
giả thiết suy ra xyz3 (trái với điều giả sử). Nên điều giả sử sai, tức là xyz3 (1) 2 Từ giả thiết suy ra 2 2 2
x y z chẵn. Có 2 TH: 0,25
- TH1: Cả 3 số đều chẵn suy ra xyz8 (2) 0,25
- TH 2: Có 1 số chẵn, 2 số lẻ. Không mất tính tổng quát giả sử 0,25 2 x chẵn, 2 2
y , z lẻ, suy ra x chẵn, y và z lẻ. Kết hợp 2 2 2
x y z 2xyz suy ra VP⁝4, mà 2 x ⁝4 nên 0,25 2 2
y z 4 (*). Do y, z lẻ nên đều chia 4 dư 1, do đó 2 2 y z chia
4 dư 2 (vô lý với *). Nên không xảy ra trường hợp này.
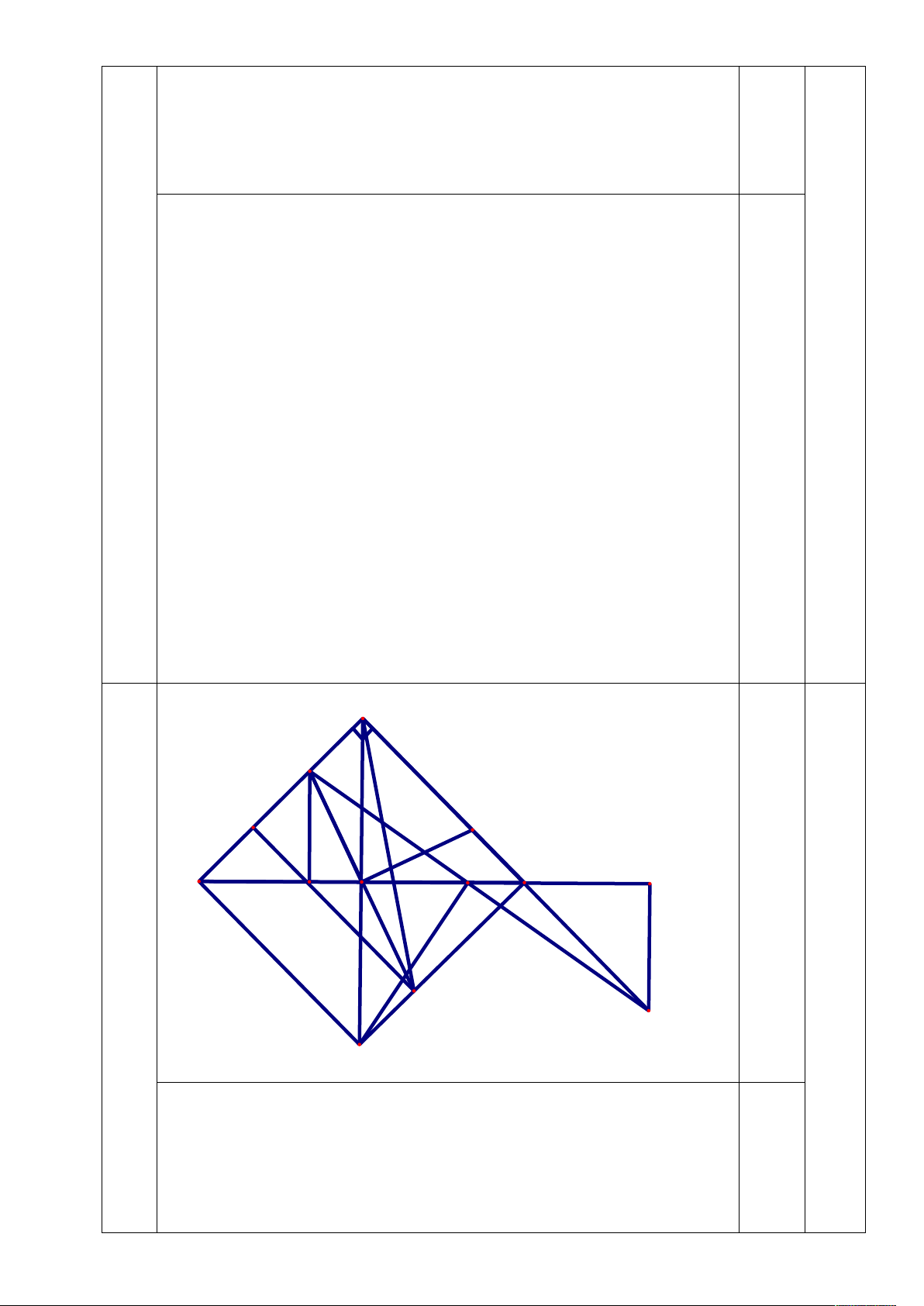
Từ (1), (2) và (3,8)=1 nên xyz24 (đpcm) 0,5 4 0,5 2,5 A G H K I C F B E D N H M
a) Chứng minh BG = CH, IG = IH
Chứng minh được góc ABD = góc FCH = 450 0,5
Chứng minh được ∆BGE = ∆CHF (g-c-g) nên BG = CH 0,5
Do GE//HF (cùng vuông góc với BC) nên góc EGI = góc FHI 0,5 ∆GEI = ∆HFI (g-c-g) suy ra đpcm 0,5
b) Chứng minh MI vuông góc GH 2
Do tam giác ABC cân A có AD là trung tuyến nên AD là đường
trung trực của BC do đó MB = MC 0,5 Chứng minh góc ABM = 900 0,25
Chứng minh được ∆GBM= ∆HCM (c-g-c) nên MG = MH 0,5 suy ra ∆GMH cân tại M, 0,25
lại có MI là đường trung tuyến nên MI vuông góc GH (đpcm) 0,5
c) Chứng minh DG + DK ≥ AG + AK 1,5
Do tam giác ADC vuông có 2 góc đáy 45 độ nên tam giác ADC 0,25 cân, suy ra AD = DC
Chứng minh được ∆AGD = ∆CKD (góc DAG = góc DCK= 450
,AD=DC, góc ADG = góc KDC do cùng phụ góc ADK). Do đó 0,25 DG = DK , AG = CK Kéo dài GD cắt MC tại N
chứng minh được ∆GBD = ∆NCD (g-c-g) suy ra GD = ND= DK 0,25
Từ đó có DG + DK = DG + DN = GN
Kẻ NH vuông góc AB tại H, chứng minh ∆AHN = ∆NCA (cạnh 0,25
huyền – góc nhọn), suy ra NH = AC.
Lại có AK + AG = AK + KC = AC= NH 0,25
Mà NH ≤ GN suy ra AK + AG ≤ DG + DK 0,25
Dấu “=” xảy ra khi E là trung điểm của BD 5 Đặt A = 2n 3m
4 . Xét các trường hợp sau: 1 - TH 1: n = 0 thì 3m A 5 + Nếu m = 0: loại + Nếu m 1 thì 3m A
5 chia 3 dư 2: A không phải số 0,25 chính phương: loại - TH2: n= 1 thì 3m A 6 + Nếu m= 0: loại + Nếu m = 1 thì 3m A 6 9: thỏa mãn 0,25
+ Nếu m 2 ; giả sử 3m 6 là số chính phương thì m 2
3 6 x , suy ra x chia hết cho 3 nên 2 x chia hết cho 9
mà VT không chia hết cho 9: vô lý, loại
- TH3: n =2 xét tương tự TH1 tìm được m = 0 0,25
- TH4: n 3 thì 2n 44 ,
+ Nếu m lẻ: chứng minh được 3m chia 4 dư 3 nên A chia 4
dư 3: A không là số chính phương (loại).
+ Nếu m chẵn: đặt m = 2p thì 2n 9 p A 4 , chứng 0,25
minh A chia 8 dư 5, nên A không là số chính phương Vậy ( ; m n) {(1;1);(0;2)}
(Học sinh có cách giải khác, đúng vẫn cho điểm tối đa).




