ĐỀ 1
Câu 1 (1,5 điểm) Tuổi thọ (Đv: năm) của một loài vật là biến ngẫu nhiên X có hàm mật độ xác suất: 2
f(x)={ k(4x − 𝑥 , khi x ∈ [0,4] 0 , khi x  [0,4] a.
Tính xác suất để sinh vật chết trước 1 năm? b.
Tính tuổi thọ trung bình của loài vật này?
Câu 2 (1,5 điểm) Để nắm tình hình đi học bằng phương tiện công cộng của sinh
viên, một trường đại học điều tra 144 sinh viên thì thấy có 40 sinh viên đi học bằng
xe Bus, với mức ý nghĩa 5%, có thể cho rằng tỉ lệ sinh viên của trường đi học bằng
xe Bus chiếm tối thiểu 30% hay không?
Câu 3 (3,5 điểm) Khảo sát trọng lượng X của một loại sản phẩm của một nhà máy,
người ta quan sát một mẫu gồm 165 sản phẩm trong kho và có kết quả như sau:
X (gam) (15 - 17] (17 - 21] (21 - 23] (23 - 25] (25 - 27] Số lượng 8 32 81 35 9 a.
Những sản phẩm có trọng lượng > 23g được gọi là sản phẩm loại 1. Hãy ước
lượng tỷ lệ sản phẩm loại 1 với độ tin cậy 95% b.
Có ý kiến cho rằng trọng lượng trung bình của sản phẩm tối đa là 24g. Với
mức ý nghĩa 5%, hãy kiểm định ý kiến trên? c.
Với độ tin cậy 95%, hãy ước lượng trọng lượng trung bình của sản phẩm trên?
Câu 4 (2 điểm) Một công ty có tỷ lệ nhân viên quê ở miền Bắc, Trung, Nam chiếm
tương ứng là 58%, 35%, 17%. Theo thống kê của công ty thì những nhân viên đạt
mức lương trên 1500$/tháng chiếm tương ứng theo quê là 15%, 11%, 17%. Chọn
ngẫu nhiên một nhân viên của công ty. a.
Tính xác suất để nhân viên đó có mức lương trên 1500$. b.
Biết nhân viên vừa chọn có mức lương trên 1500$. Tính xác suất để nhân viên đó quê ở miền Trung?
Câu 5 (1 điểm) Tỷ suất lợi nhuận (%/phiên giao dịch) của hai loại cổ phiếu A và B
lần lượt là biến ngẫu nhiên X, Y có bảng phân phối xác suất như sau: X -3 -1 5 Y -4 0,1 0,13 0,1 -1 0,15 0,2 0,12 6 0,02 0,12 0,06
Nếu tỷ suất lợi nhuận của cổ phiếu B là -1%/phiên thì tỷ suất lợi nhuận trung bình
của cổ phiếu A là bao nhiêu? ĐỀ 2
Câu 1 (2 điểm) Ở một trường đại học có 45% sinh viên đi làm bằng xe máy, 155
sinh viên đi làm bằng xe đạp, số còn lại đi làm bằng xe buýt, Khả năng đi học đúng
giờ dự kiến của sinh viên đi làm bằng xe máy, xe đạp, xe buýt tương ứng là 98%; 95% và 90%, a.
Tính tỷ lệ sinh viên đến trường đúng giờ dự kiến, b.
Trong số sinh viên đến trường đúng giờ dự kiến, tỷ lệ sinh viên đi làm bằng xe buýt là bao nhiêu?
Câu 2 (1,5 điểm) Điểm số môn Toán cao cấp (kí hiệu: X) và Điểm số môn xác suất
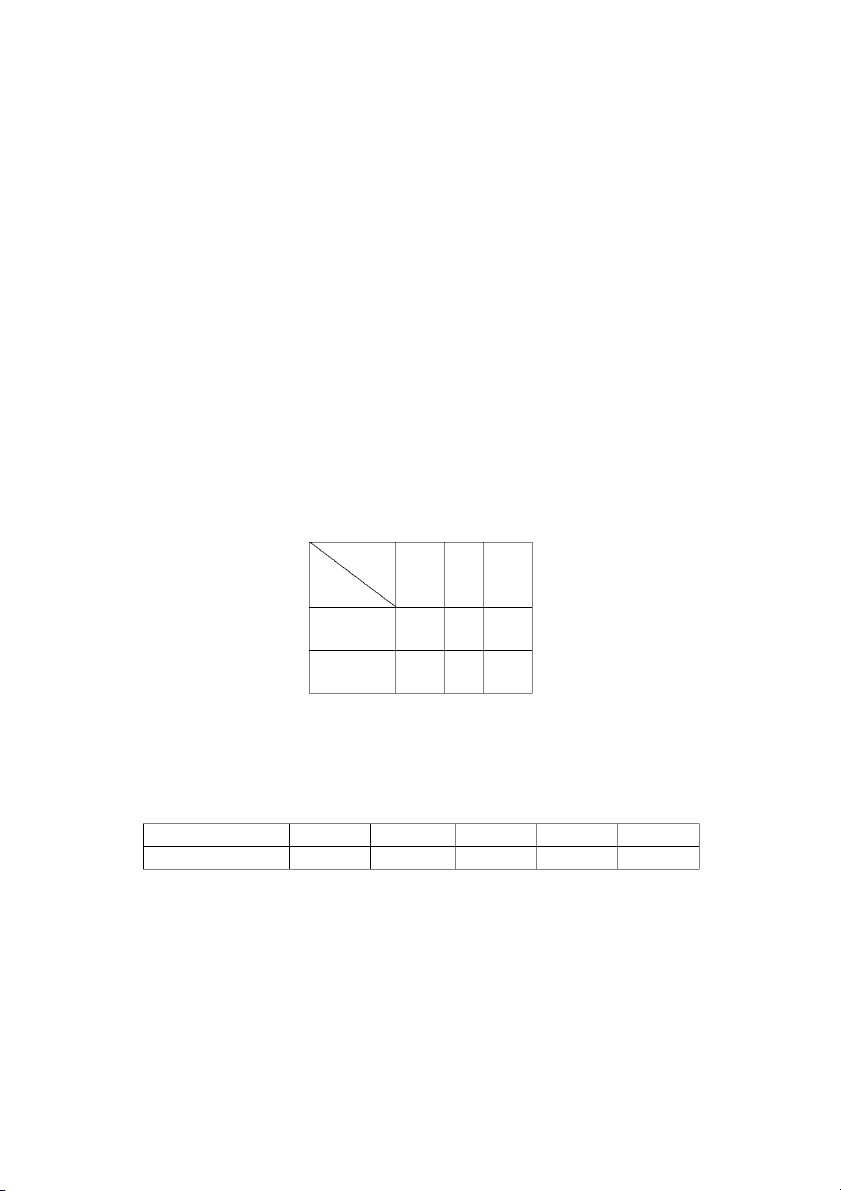
thống kê (kí hiệu: Y) là các biến ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: X 4 7 9 Y 3 0,05 0,1 0,15 6 0,1 0,2 0,15 8 0,1 0,1 0,05
Tìm điểm trung bình môn Xác suất thống kê của những bạn sinh viên có điểm môn Toán cao cấp bằng 4?
Câu 3 (2 điểm) Tuổi thọ (Đv: năm) của một loại Laptop là một biến ngẫu nhiên
liên tục có hàm mật độ như sau:
f(x) = {k(𝑥2 − 8x, khi x ∈ [0,8] 0 , khi x  [0,8] a.
Tính xác suất để Laptop không hỏng trước 6 năm? b.
Một người mua 4 Laptop loại này về dùng. Tính xác suất để có đúng 2 chiếc
không hỏng trước 6 năm?
Câu 4 (1,5 điểm) Để khảo sát tỷ lệ học sinh THPT ở Hà Nội nghiện chơi games,
người ta điều tra150 học sinh thấy có 80 em nghiện chơi games. Có ý kiến cho rằng
tỷ lệ học sinh THPT nghiện games tối thiểu là 60%. Với mức ý nghĩa 5%, hãy kiểm
định xem ý kiến đó có chính xác không?
Câu 5 (3,5 điểm) Giá một loại trà sữa (đv: nghìn/cốc) là một biến ngẫu nhiên có
phân phối chuẩn. Điều tra ngẫu nhiên 100 cửa hàng bán loại trà sữa đó thu được số liệu: Giá bán 28 29 30 31 32 33
Số cửa hàng 5 10 35 33 9 8 a.
Với độ tin cậy 95% hãy ước lượng giá bán trung bình loại trà sữa đó trên thị trường b.
Những cửa hàng bán giá lớn hơn 30 nghìn/cốc được gọi là “bán giá cao”.
Với độ tin cậy 95% hãy ước lượng tỷ lệ cửa hàng “bán giá cao” c.
Với mức ý nghĩa 5%, hãy kiểm định ý kiến cho rằng giá bán trung bình loại
trà sữa này tối đa là 31 nghìn/cốc ĐỀ 3
Câu 1 (1,5 điểm) Khảo sát 225 sinh viên về thời gian lướt Facebook trong ngày
(giờ/ngày) thấy thời gian lướt Facebook trung bình là 3 giờ/ngày và độ lệch chuẩn
là 1,5 giờ/ngày. Một nghiên cứu trước đó cho rằng thời gian lướt Facebook trung
bình của sinh viên tối thiểu là 2,5 giờ/ngày. Với mức ý nghĩa 5% hãy kiểm định xem
tài liệu đó có chính xác không, biết rằng thời gian lướt Facebook của sinh viên là
biến ngẫu nhiên có phân phối chuẩn
Câu 2 (2 điểm) Doanh thu (đơn vị: triệu đồng) hàng tháng của một cửa hàng là biến
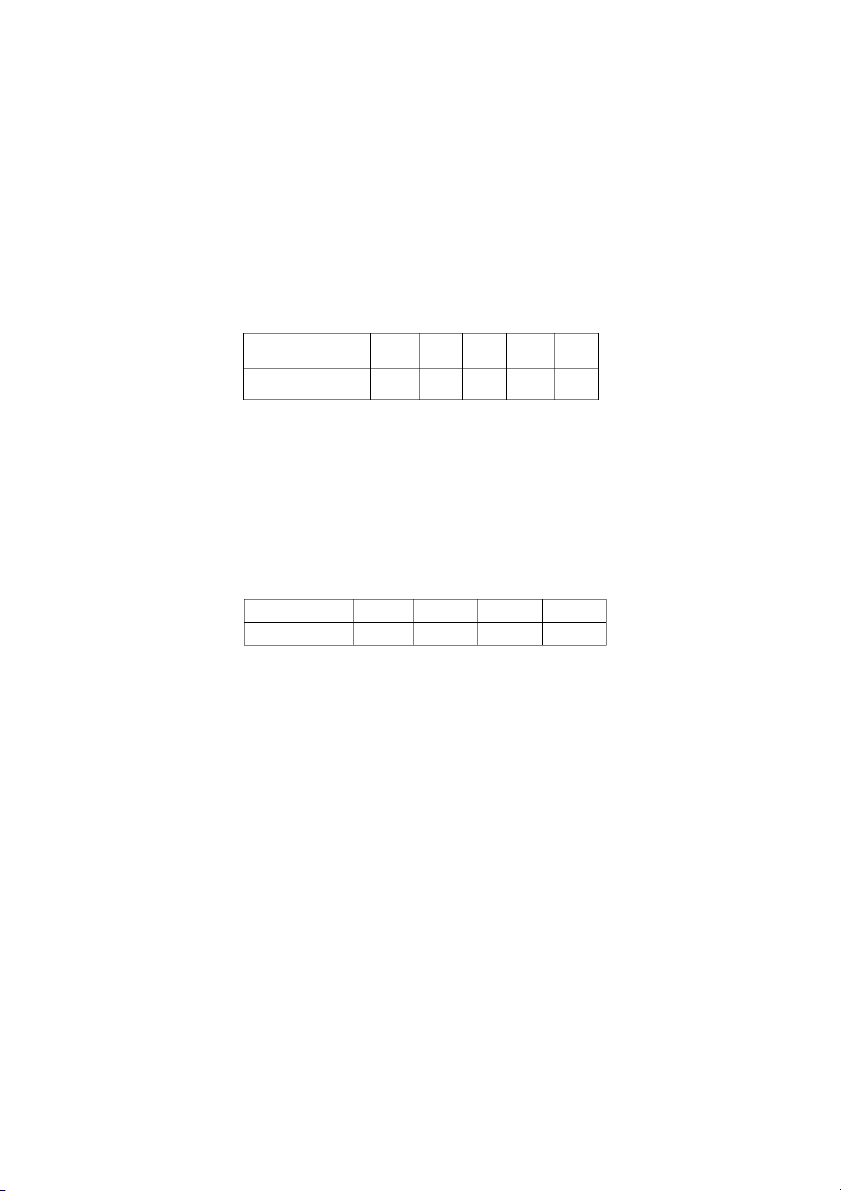
ngẫu nhiên X có bảng phân phối xác suất như sau:
Doanh thu (X) 100 105 110 115 120 P 0,15 0,2 0,4 0,15 0,1
Tính doanh thu trung bình của cửa hàng đó? Tính xác suất để cửa hàng đó có
lãi, biết chi phí cố định và chi phí khả biến lần lượt bằng 52 triệu và bằng một nửa doanh thu?
Câu 3 (3,5 điểm) Khối lượng gạo được bán hàng tháng tại các cửa hàng có quy mô
tương tự nhau trong một thành phố là một biến ngẫu nhiên phân phối chuẩn. Người
ta chọn ngẫu nhiên 36 cửa hàng để khảo sát, kết quả được cho trong bảng sau (đơn vị tấn)
Khối lượng (1- 2] (2 - 3] (3 - 4] (4 - 5] Số cửa hàng 5 12 13 6 a.
Với độ tin cậy 95%, khối lượng gạo trung bình được bán hàng tháng tối đa sẽ là bao nhiêu? b.
Theo tài liệu năm trước khối lượng gạo trung bình được bán hàng tháng tại
các cửa hàng là 3,2 (tấn). Có ý kiến cho rằng năm nay kinh doanh tốt hơn. Với mức
ý nghĩa 5%, hãy kiểm định ý kiến trên? c.
Những cửa hàng bán được khối lượng gạo nhỏ hơn hoặc bằng 2 (tấn/tháng)
được gọi là “cửa hàng kinh doanh thua lỗ”. Với độ tin cậy 95%, hãy ước lượng số
cửa hàng kinh doanh thua lỗ trên địa bàn thành phố, biết thành phố có 2000 cửa hàng kinh doanh gạo.
Câu 4 (1điểm) Tuổi thọ (đv: năm) của một loại Tivi tuân theo phân phối chuẩn với
tuổi thọ trung bình là 5 và độ lệch chuẩn 2. Thời gian bảo hành là 3 năm. Hãy xác
định tỷ lệ bảo hành của loại Tivi này?
Câu 5 (2 điểm) Giả sử bạn đầu tư vào hai cổ phiếu A và B có lãi suất theo tháng
(đv:%) được cho dưới dạng bảng phân phối xác suất đồng thời như sau: B -2 -1 3 4 A -1 0,01 0,04 0,1 0,05 3 0,05 0,25 0,15 0,1 5 0,1 0,05 0,1 0
Tính lãi suất trung bình khi đầu tư vào cổ phiếu A nếu lãi suất cổ phiếu B bằng 3% ĐỀ 4
Câu 1 (2 điểm) Tuổi thọ (tính theo năm) của một loại Bếp điện tử là biến ngẫu nhiên
tuân theo phân phối chuẩn với tuổi thọ trung bình là 5 năm và độ lệch chuẩn là 2
năm. Thời gian bảo hành là 3 năm. a.
Tìm tỷ lệ bảo hành của loại Bếp điện tử đó b.
Một người mua 5 bộ Bếp để tặng cho gia đình bạn bè. Tính xác suất để có
đúng 2 bộ bếp phải bảo hành.
Câu 2 (2 điểm) Khi đầu tư vào thị trường Vàng và Ngoại tệ thì lãi suất X và Y
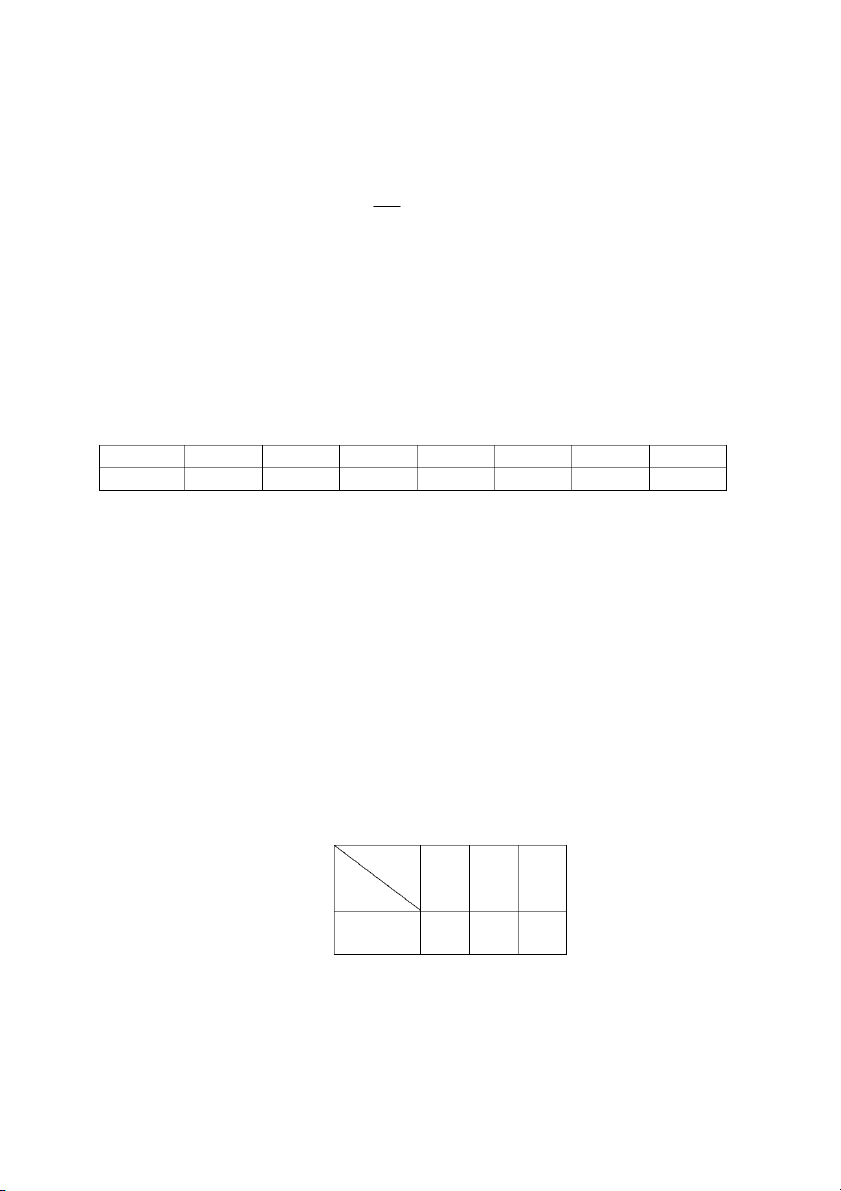
(đv:%) là các biến ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: X -3 2 4 Y -2 0,05 0,1 0,15 2 0,1 0,2 0,15 5 0,1 0,1 0,5
Tính lãi suất trung bình khi đầu tư vào thị trường ngoại tệ biết năm đó lãi suất thị trường vàng bằng 2%
Câu 3 (1 điểm) Tuổi thọ (Đv: năm) của một loại bóng đèn là một biến ngẫu nhiên
liên tục có hàm mật độ như sau: 3
f(x)= { 𝑥2 , 𝑘ℎ𝑖 𝑥 ∈ [0,2] 8 0 , khi x [0,2]
Tìm tuổi thọ trung bình của loại bóng đèn này?
Câu 4 (1,5 điểm) Để khảo sát tỷ lệ sinh viên của một trường đại học tham gia bán
hàng ĐA CẤP, người ta điều tra 100 sinh viên thấy có 21 em tham gia. Có ý kiến
cho rằng có tối thiểu 15% sinh viên tham gia bán hàng ĐA CẤP. Với mức ý nghĩa
5% hãy kiểm định xem ý kiến đó có chính xác không?
Câu 5 (3,5 điểm) Giá một loại trà sữa (đv: nghìn/cốc) là một biến ngẫu nhiên có
phân phối chuẩn. Điều tra ngẫu nhiên 64 cửa hàng bán loại trà sữa đó thu được số liệu: Giá bán 30 32 34 36 38 Số cửa hàng 6 15 18 17 8 a.
Với độ tin cậy 95% hãy ước lượng giá bán trung bình loại trà sữa đó trên thị trường b.
Những cửa hàng bán giá lớn hơn 35 nghìn/cốc được gọi là “bán giá cao”. Với
độ tin cậy 95% hãy cho biết có tối đa bao nhiêu phần trăm cửa hàng “bán giá cao”? c.
Những cửa hàng bán giá nhỏ hơn 31 nghìn/cốc được gọi là “bán phá giá”. Một
chuyên gia trong lĩnh vực trà sữa cho rằng có hơn 10% tổng số cửa hàng bán phá
giá. Với mức ý nghĩa 5%, hãy kiểm định ý kiến trên? ĐỀ 5
Câu 1 (1,5 điểm) Một doanh nghiệp sản xuất khẩu trang y tế để xuất khẩu có ba
phân xưởng 1,2 và 3 sản xuất với sản lượng chiếm tỷ lệ tương ứng là 35%, 20% và
45%. Tỷ lệ khẩu trang đạt tiêu chuẩn xuất khẩu của phân xưởng 1,2 và 3 lần lượt là
90%, 92% và 95%. Tính tỷ lệ khẩu trang đạt tiêu chuẩn xuất khẩu của nhà máy.
Câu 2 (2 điểm) Trọng lượng của một loại sản phẩm do nhà máy sản xuất có phân
phối chuẩn với trọng lượng trung bình 10kg và độ lệch chuẩn là 0,2kg. Một sản phẩm
được gọi là đạt chuẩn nếu có trọng lượng từ 9,6kg đến 10,4kg a.
Tính tỷ lệ sản phẩm đạt chuẩn do nhà máy sản xuất. b.
Lấy ngẫu nhiên 8 sản phẩm của nhà máy, tính xác suất lấy được ít nhất 6 sản phẩm đạt chuẩn.
Câu 3 (1,5 điểm) Doanh thu (đv: triệu đồng) hàng tháng của một cửa hàng là biến
ngẫu nhiên X có hàm phân phối xác suất như sau:
Doanh thu (X) 100 120 140 160 180 P 0,05 0,35 0,3 0,2 0,1 a.
Tính doanh thu trung bình của cửa hàng đó? b.
Chi phí cố định của cửa hàng là 35 triệu đồng, chi phí khả biến bằng một
phần hai doanh thu. Tính xác suất để cửa hàng lãi hơn 40 triệu?
Câu 4 (3,5 điểm) Số lượng gạo bán hàng ngày tại một cửa hàng là biến ngẫu nhiên
có phân phối chuẩn. Tiến hành khảo sát số lượng gạo bán hàng ngày tại một cửa
hàng, người ta thu được bảng số liệu sau:
SL gạo (kg) (110 - 125] (125- 140] (140- 155] (155- 170] (170- 185] (185- 200] Số ngày 12 28 76 79 21 9 a.
Những ngày bán được lượng gạo >170kg được gọi là ngày “cao điểm”. Ước
lượng tỷ lệ những ngày cao điểm với độ tin cậy 95%. b.
Chủ cửa hàng cho rằng trung bình mỗi ngày không bán quá 160kg. Từ số
liệu điều tra trên với mức ý nghĩa 5% hãy cho biết chủ cửa hàng nói có đúng không? c.
Ước lượng lượng gạo trung bình bán được hàng ngày với độ tin cậy 98%?
Câu 5 (1,5 điểm) Theo báo cáo của một tổ chức giáo dục thì tỷ lệ sinh viên thích
học online là 80%. Để kiểm tra tính chính xác của báo cáo này, cơ quan quản lý
giáo dụ cho điều tra 121 sinh viên đang học theo hình thức online thì thấy có 92
sinh viên thích hình thức học này. Với mức ý nghĩa 5%, hãy cho biết tính chính xác của báo cáo trên? ĐỀ 6
Câu 1 (2 điểm) Một cửa hàng kinh doanh đồ điện tử trong đó sản phẩm laptop được
sản xuất bởi 3 hãng A,S và D với cơ cấu sản phẩm như sau: hãng A chiếm 45%,
hãng S chiế 35% và phần còn lại là của hãng D. Tỷ lệ sản phẩm bị lỗi của các hãng
A, S, D lần lượt là 1,5%, 2% và 3%. a.
Chọn ngẫu nhiên một chiếc laptop, hãy tính xác suất để chiếc laptop đó mắc lỗi b.
Tính xác suất để trong 15 chiếc laptop được chọn, có nhiều hơn 1 chiếc mắc lỗi.
Câu 2 (2 điểm) Tuổi thọ (đv: năm) của một loại sản phẩm điện tử tuân theo phân
phối chuẩn với tuổi thọ trung bình là 3 và độ lệch chuẩn 1, Thời gian bảo hành là 2 năm. a.
Tỷ lệ bảo hành của loại sản phẩm điện tử này là bao nhiêu? b.
Mua 8 sản phẩm, tính xác suất để có ít nhất một sản phẩm phải bảo hành
Câu 3 (1,5 điểm) Gọi X là biến ngẫu nhiên thể hiện giới tính (X=0 nếu là nữ, X=1
nếu là nam), Y là biến ngẫu nhiên biểu diễn thời gian (giờ) lướt Facebook trong một
ngày của sinh viên và (X;Y) có bảng phân phối đồng thời như sau: X 1 Y 2 3 0 0,15 0,2 0,2 1 0,2 0,1 0,15
Hãy cho biết thời gian lướt Facebook trung bình của sinh viên nữ có lớn hơn
thời gian lướt Facebook trung bình của sinh viên nam hay không?
Câu 4 (2,5 điểm) Khảo sát cân nặng của 130 con gia cầm của trang trại thu được bảng sau:
Số cân nặng (kg) (2,2 - 2,3] ( 2,3 - 2,4] (2,4 - 2,5] (2,5 - 2,6] (2,6 - 2,7] Số con 5 40 60 21 4
Biết trọng lượng mỗi con gia cầm tuân theo phân phối chuẩn. a.
Với độ tin cậy 95%, hãy ước lượng trọng lượng trung bình của những con gia
cầm trong trang trại này. b.
Những con gia cầm có trọng lượng nhỏ hơn hoặc bằng 2,4kg được gọi là chậm
lớn. Với mức ý nghĩa 5%, hãy kiểm định ý kiến cho rằng: “tỷ lệ những con gia cầm
chậm lớn của trang trại này nhỏ hơn 35%”.
Câu 5 (2 điểm) Trong một đợt vận động bầu cử tổng thống người ta phỏng vấn ngẫu
nhiên 2000 cử tri thì được biết 1335 người trong số đó sẽ bỏ phiếu cho ứng viên A. a.
Với độ tin cậy 95%, hãy ước lượng tỉ lệ tối thiểu số phiếu ủng hộ ứng viên A? b.
Với mức ý nghĩa 5%, hãy kiểm định ý kiến cho rằng tỷ lệ cử tri ủng hộ ứng viên A là trên 70%? ĐỀ 7
Câu 1 (2 điểm) Mức tiêu hao nhiên liệu của một loại xe hơi là biến ngẫu nhiên tuân
theo phân phối chuẩn với mức tiêu hao nhiên liệu trung bình  = 8 lít/100km và độ
lệch chuẩn  = 1,5 lít/100km. a.
Tìm xác suất để mua được một chiếc xe có mức tiêu hao nhiên liệu nhỏ hơn 7 lít/100km b.
Một người mua 5 chiếc xe hơi đó, tính xác suất để người này mua được ít nhất
2 xe có mức tiêu hao nhiên liệu nhỏ hơn 7 lít/100km.
Câu 2 (2 điểm) Khi đầu tư vào hai thị trường A và B lãi suất XA và XB (đv: %/phiên)
là các biến ngẫu nhiên có bảng phân phối xác suất đồng thời như sau: XA -4 X -1 6 B -3 0,05 0,1 0,15 -1 0,1 0,2 0,15 5 0,1 0,1 0,05
Tìm lãi suất trung bình khi đầu tư vào thị trường B biết năm đó lãi suất thị trường A là 6%
Câu 3 (1 điểm) Tuổi thọ (Đv: năm) của một loại động vật là một biến ngẫu nhiên
liên tục có hàm mật độ xác suất như sau: 1
f(x)= { 𝑥2 , 𝑘ℎ𝑖 𝑥 ∈ [0,3] 9 0 , khi x [0,3]
Tìm tuổi thọ trung bình của loại động vật này?
Câu 4 (1,5 điểm) Giá bán nhà (đv: triệu/ m2) ở khu vực ngoại ô Hà Nội là một biến
ngẫu nhiên tuân theo quy luật phân phối chuẩn. Một công ty bất động sản điều tra
ngẫu nhiên 25 ngôi nhà được bán gần đây thu được giá trung bình là 22 triệu/m2, với
mức ý nghĩa 5% hãy kiểm định ý kiến trên.
Câu 5 (3,5 điểm) Giá một loại bánh (đv: nghìn/1 hộp) là một biến ngẫu nhiên có
phân phối chuẩn. Điều tra ngẫu nhiên 400 cửa hàng bán loại bánh đó thu được số liệu: Giá bán 83 85 87 89 91 93 95 97 99 101 Số cửa hàng 15 31 36 65 110 60 33 21 17 12 a.
Với độ tin cậy 95% hãy ước lượng giá bán trung bình của loại bánh đó. b.
Với độ tin cậy 95% nhưng muốn độ chính xác của ước lượng nhỏ hơn 0,2 thì
cần điều tra một mẫu với kích thước tối thiểu là bao nhiêu? c.
Những cửa hàng bán giá lớn hơn hoặc bằng 92 nghìn/1 hộp được gọi là “bán
giá cao”. Với mức ý nghĩa 5% hãy kiểm định ý kiến cho rằng tỷ lệ cửa hàng “bán giá cao” lớn hơn 20%. ĐỀ 8
Câu 1 (1 điểm) Cho tuổi thọ của một loài sinh vật A là biến ngẫu nhiên X có hàm
mật độ xác xuất như sau: 4 f(x)= { , 𝑘ℎ𝑖 𝑥 ∈ [1,4] 3𝑥2 0 , khi x [1,4]
Tìm tuổi thọ trung bình của loài sinh vật A?
Câu 2 (1,5 điểm) Trọng lượng đóng gói đường loại 500g một gói trên máy tự động
là một biến ngẫu nhiên có phân phối chuẩn. Kiểm tra 100 gói thu được trọng lượng
trung bình là 495g và độ lệch chuẩn là 10g. Với mức ý nghĩa 5% có thể cho rằng
trọng lượng trung bình của những gói đường đó bị đóng thiếu hay không?
Câu 3 (3,5 điểm) Khảo sát trọng lượng X của một loại sản phẩm của một nhà máy,
người ta quan sát một mẫu gồm 400 sản phẩm trong kho và có kết quả như sau:
X (gam) (11- 15] (15- 19] (19- 23] (23- 27] (27- 31] (31- 35] (35- 39] Số lượng 30 40 65 90 85 50 40 a.
Những sản phẩm có trọng lượng ≤23g được gọi là sản phẩm loại II. Hãy ước
lượng ti lệ sản phẩm loại II với độ tin cậy 95%. b.
Có ý kiến cho rằng tỷ lệ sản phẩm loại II tối đa là 35%, với mức ý nghĩa 5%
hãy kiểm định ý kiến trên? c.
Ước lượng trọng lượng trung bình tối thiểu của sản phẩm trên với độ tin cậy 95%
Câu 4 ( 2 điểm) Một lô hàng được phân làm 3 loại. Loại I chiếm 2/3 số sản phẩm
của lô hàng, loại 2 chiếm 1/4 còn lại là loại III. Trong các thùng loại I có 80% sản
phẩm đạt tiêu chuẩn, loại II có 60% sản phẩm đạt tiêu chuẩn, loại III có 40% sản
phẩm đạt tiêu chuẩn. Lấy ngẫu nhiên 1 sản phẩm của lô hàng. a.
Tính xác suất để lấy được sản phẩm đạt tiêu chuẩn. b.
Tính xác suất để sản phẩm đạt tiêu chuẩn đó là của thùng loại I?
Câu 5 (2 điểm) Tỷ suất lợi nhuận (%/phiên giao dịch ) của hai loại cổ phiếu A và B
lần lượt là biến ngẫu nhiên X, Y có bảng phân phối xác suất như sau: X -3 Y -1 5 -4 0,1 0,13 0,1 -1 0,15 0,2 0,12 6 0,02 0,12 0,06
Nếu tỷ suất lợi nhuận của cổ phiếu B là -1%/phiên thì tỷ suất lợi nhuận trung bình
của cổ phiếu A là bao nhiêu? ĐỀ 9
Câu 1 (1,5 điểm) Khảo sát 196 sinh viên về thời gian tự học trong ngày (giờ/ ngày),
thấy thời gian tự học trung bình là 2 giờ/ngày và độ lệch chuẩn là 1,5 giờ/ngày. Một
nghiên cứu trước đó cho rằng thời gian tự học bình quân của sinh viên tối thiểu là
2,3 giờ/ngày. Với mức ý nghĩa 5%, hãy kiểm định xem tài liệu đó có chính xác
không, biết rằng thời gian tự học của sinh viên là biến ngẫu nhiên phân phối chuẩn.
Câu 2 (2 điểm) Doanh thu (đv: triệu đồng) hàng tháng của một cửa hàng là biến
ngẫu nhiên X có bảng phân phối xác suất như sau:
Doanh thu (X) 100 105 110 115 120 P 0,15 0,2 0,4 0,15 0,1
Tính doanh thu trung bình của cửa hàng đó? Tính xác suất để cửa hàng đó có lãi hơn
15 triệu/tháng, biết chi phí cố định và chi phí khả biến lần lượt bằng 40 triệu và bằng một nửa doanh thu?
Câu 3 (3,5 điểm) Khối lượng bột mì được bán hàng tháng tại các đại lý có quy mô
tương tự nhau trong một tỉnh là một biến ngẫu nhiên phân phối chuẩn. Người ta khảo
sát ngẫu nhiên 100 đại lý để khảo sát, kết quả được cho trong bảng sau (đơn vị tấn)
Khối lượng (1- 2] (2 - 3] (3 - 4] (4 - 5] Số cửa hàng 11 42 38 9 a.
Với độ tin cậy 95%, khối lượng bột mì trung bình được bán hàng tháng tối đa sẽ là bao nhiêu? b.
Theo tài liệu năm trước khối lượng gạo trung bình được bán hàng tháng tại
các đại lý là 3,2 (tấn). Có ý kiến cho rằng năm nay kinh doanh tốt hơn. Với mức ý
nghĩa 5%, hãy kiểm định ý kiến trên? c.
Những đại lý bán được khối lượng bột mì nhỏ hơn hoặc bằng 2 (tấn/tháng)
được gọi là “đại lý kinh doanh thua lỗ”. Với độ tin cậy 95%, hãy ước lượng số đại
lý kinh doanh thua lỗ trên địa bàn tỉnh, biết tỉnh có 1000 đại lý kinh doanh bột mì.
Câu 4 (1 điểm) Tuổi thọ (đv: năm) của một loại Điện thoại tuân theo phân phối
chuẩn với tuổi thọ trung bình là 5 và độ lệch chuẩn 2. Thời gian bảo hành 3 năm.
Hãy xác định tỉ lệ bảo hành của loại Điện thoại này?
Câu 5 (2 điểm) Giả sử bạn đầu tư vào hai cổ phiếu A và B có lãi suất theo tháng
(đv:%) được cho dưới dạng bảng phân phối xác suất đồng thời như sau: B -2 A -1 3 4 -1 0,01 0,04 0,1 0,05 3 0,05 0,25 0,15 0,1 5 0,1 0,05 0,1 0
Tính lãi suất trung bình khi đầu tư vào cổ phiếu A nếu lãi suất cổ phiếu B bằng 3% ĐỀ 10
Câu 1 (2 điểm) Thời gian từ lúc vay đến lúc trả của một khách hàng tại ngân hàng
Seabank là đại lượng ngẫu nhiên có phân phối chuẩn với thời gian trung bình từ lúc
vay đến lúc trả là 18 tháng và độ lệch chuẩn là 4 tháng. a.
Tính tỷ lệ khách hàng có thời gian từ lúc vay đến lúc trả là trên 2 năm b.
Tính xác suất để trong 5 khách hàng, có đúng 2 khách hàng có thời gian từ lúc
vay đến lúc trả là trên 2 năm.
Câu 2 (1,5 điểm) Tỷ suất lợi nhuận trên vốn đầu tư của hai loại cổ phiếu A, B trên
thị trường chứng khoán Việt Nam (đv: %) tương ứng là các đại lượng ngẫu nhiên X,
Y và có bảng phân phối xác suất đồng thời như sau: Y -2 X 0 5 10 0 0 0,05 0,05 0,1 4 0,05 0,1 0,25 0,15 6 0,1 0,05 0,1 0
Tính lãi suất lợi nhuận trung bình khi đầu tư vào cổ phiếu B, biết tỷ suất lợi nhuận cổ phiếu A bằng 4%
Câu 3 (1,5 điểm) Một cửa hàng điện máy nhập lô hàng bao gồm: 8 sản phẩm loại
1; 7 sản phẩm loại 2 và 5 sản phẩm loại 3. Biết rằng xác suất để mỗi sản phẩm loại
1, 2, 3 tương ứng bị hỏng trong quá trình vận chuyển là 1%; 1,5%; và 1,8%. Sau khi
lô hàng đó vận chuyển về kho của cửa hàng, người ta lấy ra ngẫu nhiên một sản
phẩm để kiểm tra. Tính xác suất để sản phẩm lấy ra này bị hỏng?
Câu 4 (2,5 điểm) Để nghiên cứu năng suất lao động của công nhân nhà máy Z,
người ta chọn ngẫu nhiên 81 công nhân ở nhà máy đó để xem năng suất lao động
của họ, thấy năng suất trung bình là 17,2 (sản phẩm/ngày); độ lệch chuẩn là 2,4 (sản phẩm/ngày). a.
Với độ tin cậy 0,95, hãy ước lượng năng suất lao động trung bình của công nhân nhà máy Z b.
Có ý kiến cho rằng năng suất trung bình của công nhân nhà máy Z tối thiểu là
16 (sản phẩm/ngày). Với mức ý nghĩa 5%, hãy kiểm định ý kiến trên?
Câu 5 (2,5 điểm) Giá một loại bánh (đv; nghìn/1 hộp) là một biến ngẫu nhiên có
phân phối chuẩn. Điều tra ngẫu nhiên một số cửa hàng bán loại bánh đó thu được số liệu: Giá bán 85 87 89 91 93 95
Số cửa hàng 5 15 65 63 17 6 a.
Những cửa hàng bán giá lớn hơn 92 nghìn/1 hộp được gọi là “bán giá cao”.
Với mức ý nghĩa 5% hãy kiểm định ý kiến cho rằng tỷ lệ cửa hàng “bán giá cao” lớn hơn 20% b.
Những cửa hàng bán giá thấp hơn 88 nghìn/1 hộp được gọi là “bán giá thấp”.
Với độ tin cậy 95%, hãy ước lượng tỷ lệ cửa hàng “bán giá thấp”. ĐỀ 11
Câu 1 (1,5 điểm) Tuổi thọ (đv: năm) của một loại Điện thoại tuân theo phân phối
chuẩn với tuổi thọ trung bình là 5 và độ lệch chuẩn 2. Thời gian bảo hành là 3 năm.
Hãy xác định tỷ lệ bảo hành của loại điện thoại này?
Câu 2 (1,5 điểm) Để nắm được nhu cầu thuê trọ của sinh viên khi chuyển sang cơ
sở mới, một trường đại học đã tiến hành điều tra khảo sát 200 sinh viên của họ, thấy
có 124 sinh viên có nhu cầu thuê trọ. Với mức ý nghĩa 5% có thể cho rằng có ít nhất
55% sinh viên của trường đại học này có nhu cầu thuê trọ hay không?
Câu 3 (3,5 điểm) Khối lượng bột mì được bán hàng tháng tại các đại lý có quy mô
tương tự nhau trong một tỉnh là một biến ngẫu nhiên phân phối chuẩn. Người ta khảo
sát ngẫu nhiên 100 đại lý để khảo sát, kết quả được cho trong bảng sau (đơn vị tấn)
Khối lượng (1- 2] (2 - 3] (3 - 4] (4 - 5] Số cửa hàng 8 41 39 12 a.
Với độ tin cậy 95%, khối lượng bột mì trung bình được bán hàng tháng tối đa sẽ là bao nhiêu? b.
Theo tài liệu năm trước khối lượng gạo trung bình được bán hàng tháng tại
các đại lý là 3,2 (tấn). Có ý kiến cho rằng năm nay kinh doanh tốt hơn. Với mức ý
nghĩa 5%, hãy kiểm định ý kiến trên? c.
Những đại lý bán được khối lượng bột mì nhỏ hơn hoặc bằng 2 (tấn/tháng)
được gọi là “đại lý kinh doanh thua lỗ”. Với độ tin cậy 95%, hãy ước lượng số đại
lý kinh doanh thua lỗ trên địa bàn tỉnh, biết tỉnh có 1000 đại lý kinh doanh bột mì.
Câu 4 (2 điểm) Một lô hàng được phân làm 2 loại thùng. Thùng loại I chiếm 60%
số sản phẩm của lô hàng. Trong các thùng loại I có chứa 80% sản phẩm đạt tiêu
chuẩn, loại II có 70% sản phẩm đạt tiêu chuẩn. Lấy ngẫu nhiên một thùng rồi sau đó
lấy ngẫu nhiên một sản phẩm từ thùng đó. a.
Tính xác suất để lấy được sản phẩm đạt tiêu chuẩn. b.
Tính xác suất để sản phẩm đạt tiêu chuẩn đó là của thùng loại II?
Câu 5 (1,5 điểm) Tỷ suất lợi nhuận (%/phiên giao dịch) của hai loại cổ phiếu A và
B lần lượt là biến ngẫu nhiên X, Y có bảng phân phối xác suất như sau: X -4 Y -1 5 -4 0,1 0,13 0,1 -2 0,1 0,2 0,12 6 0,04 0,12 0,09
Nếu tỷ suất lợi nhuận của cổ phiếu B là 6%/phiên thì tỷ suất lợi nhuận trung bình
của cổ phiếu A là bao nhiêu?