
Preview text:
TT Mã câu Nội dụng câu hỏi Đáp Loại Cố Nhóm hỏi án câu định 1 C1-1- D Nhóm 1 001
Một sinh viên lên bốc thăm 2 trong số 20 câu hỏi
để trả lời. Cho biết sinh viên này chỉ nắm được
kiến thức của 15 trong số 20 câu hỏi đó. Tính
xác suất sinh viên này trả lời được ít nhất một câu hỏi: A. 15/19 B. 16/19 C. 17/19 D. 18/19 2 C1-1-
Một hộp đựng 10 quả cầu gồm: 2 quả màu đỏ, 3 Nhóm 1 002
quả vàng và 5 quả xanh. Chọn ngẫu nhiên từ hộp A
đó ra 4 quả cầu. Xác suất chọn được 1 quả màu
đỏ, 1 quả vàng và 2 quả xanh là: A. 0,2857 B. 0,1793 C. 0,1097 D. 0,0973. 3 C1-1-
Một hộp có 5 sản phẩm trong đó có 2 sản phẩm B Nhóm 1 003
tốt. Chọn ngẫu nghiên 2 sản phẩm. Xác suất để
lấy được 2 sản phẩm tốt là: A. 0,2 B. 0,1 C. 0,3 D. 0,05 4 C1-1-
Trên giá sách có 4 quyển sách toán, 3 quyển sách A Nhóm 1 004
lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển
sách. Tính xác suất để 3 quyển được lấy ra thuộc 3 môn khác nhau: A. 2/7 B. 1/21 C. 37/42 D. 5/42 5 C1-1-
Một hộp đựng 10 quả cầu gồm: 2 quả màu đỏ, 3 B Nhóm 1 005
quả vàng và 5 quả xanh. Chọn ngẫu nhiên từ hộp
đó ra 4 quả cầu. Xác suất chọn được 2 quả màu xanh là: A. 0,2894 B. 0,4762 C. 0,0952 D. 0,0476 6 C1-1-
Có hai thùng, thùng 1 có 10 bi trắng và 5 bi đỏ; A Nhóm 1 006
thùng 2 có 8 bi trắng và 4 bi đỏ. Lấy ngẫu nhiên
lần lượt mỗi thùng một quả. Xác suất để lấy
được ít nhất một quả đỏ: A. 5/9 B. 7/9 C. 4/9 D. 1/9 7
Có hai thùng, thùng thứ nhất có 10 bi trắng và 5 D Nhóm 1
bi đỏ; thùng thứ hai có 8 bi trắng và 4 bi đỏ. Lấy C1-1-
ngẫu nhiên lần lượt mỗi thùng một quả. Xác suất 007
để lấy được hai quả cùng mầu: A. 2/9 B. 4/9 C. 7/9 D. 5/9 8 C2-1-
Lợi nhuận X (đơn vị: triệu đồng) thu được khi B Nhóm 2 008
đầu tư vào một dự án có bảng phân phối xác suất như sau: X -300 -200 -100 0 100 300 P 0,05 0,1 0,1 0,2 0,25 0,2
Lợi nhuận trung bình khi đầu tư vào dự án này là bao nhiêu? A. 70 B. 80 C. 100 D. 90 9 C2-1-
Lợi nhuận X (đơn vị: triệu đồng) thu được khi A Nhóm 2 009
đầu tư vào một dự án có bảng phân phối xác suất như sau: X -300 -200 -100 P 0,05 0,1 0,1
Khả năng dự án này thu được lợi nhuận nhiều
hơn 100 triệu đồng là bao nhiêu? A. 30% B. 40% C. 20% D. 35% 10 C2-1-
Số lượng xe ô tô TOYOTA (ký hiệu là X) mà D Nhóm 2 010
một đại lý bán được trong một tuần có bảng phân phôi xác suất như sau: X 0 1 2 P 0,05 0,13 0,12
Xác suất để đại lý đó bán được ít nhất 4 xe trong một tuần là: A. 0,32 B. 0,39 C. 0,07 D. 0,35 11 C2-1-
Tuổi thọ ( đơn vị: năm) của một loại thiết bị điện C Nhóm 3 011
tử là biến ngẫu nhiên có hàm mật độ: 2
k(x 3x) khi x 0,3 f (x) 0 khi x 0,3
Xác suất để thiết bị đó hỏng trước một năm là: A. 11/27 B. 5/27 C. 7/27 D. 8/27 12 C2-1-
Tuổi thọ ( đơn vị: năm) của một loại thiết bị điện A Nhóm 3 012
tử là biến ngẫu nhiên có hàm mật độ: 2
k(x 3x) khi x 0,3 f (x) 0 khi x 0,3
Xác suất để thiết bị đó không hỏng trước 2 năm là: A. 7/27 B. 8/27 C. 5/25 D. 11/27 13 C2-1-
Tuổi thọ (đơn vị: năm) của một loại thiết bị điện C Nhóm 3 013
tử là biến ngẫu nhiên có hàm mật độ: 2
k(x 3x) khi x 0,3 f (x) 0 khi x 0,3
Tuổi thọ trung bình của thiết bị đó là: A. 2 B. 1,8 C. 1,5 D. 1,2 14 C2-1-
Tuổi thọ (đơn vị: giờ) của một loại sản phẩm là A Nhóm 3 014
biến ngẫu nhiên có hàm mật độ: 0 khi x 100 4 f (x) 2.10 khi x 1 00 3 x
Tuổi thọ trung bình của loại sản phẩm này là: A.200 B.250 C.300 D.400 15 C2-1-
Tuổi thọ (đơn vị: giờ) của một loại sản phẩm là A Nhóm 3 015
biến ngẫu nhiên có hàm mật độ: 0 khi x 100 f (x) 4 2.10 khi x 1 00 3 x
Xác suất để loại sản phẩm này hỏng trước 200 giờ là: A. 75% B. 30% C. 20% D. 15% 16 C3-1-
Cho X ~B(5; 0,25). Khí đó giá trị P(X>3) bằng: C Nhóm 4 016 A.0,051625 B.0,056125 C.0,015625 D.0,025615 17 C3-1-
Thời gian X (tháng) từ lúc vay đến lúc trả tiền A Nhóm 4 017
của 1 khách hàng tại ngân hàng A là biến ngẫu
nhiên có phân phối chuẩn: N(18; 16). Tỉ lệ
khách hàng trả tiền cho ngân hàng A trong
khoảng từ 12 đến 16 tháng ? A. 24,17% B. 9,63% C. 25,17% D. 10,63% 18 C3-1-
Chiều cao của nam giới đã trưởng thành là biến D Nhóm 4 018
ngẫu nhiên X (cm) có phân phối chuẩn: N(165;
25). Tỉ lệ nam giới đã trưởng thành cao từ 1,65m đến 1,75m là: A. 1,6% B. 42,75% C. 45,96% D. 47,73% 19 C3-1-
Một lô hàng thịt đông lạnh đóng gói nhập khẩu D Nhóm 4 019
với tỉ lệ bị nhiểm khuẩn là 1,6%. Kiểm tra lần
lượt ngẫu nhiên 20 gói thịt từ lô hàng này. Tính
xác suất có từ 1 đến 3 gói thịt bị nhiểm khuẩn: A. 0,001522 B. 0,00522 C. 0,00922 D. 0,2755 20 C3-1-
Trong một kho lúa giống có tỉ lệ hạt lúa lai tạp là A Nhóm 4 020
2%. Tính xác suất sao cho khi chọn lần lượt
1000 hạt lúa giống trong kho thì có từ 17 đến 19
hạt lúa lai tạp ? (Poisson) A. 0,2492 B. 0,3492 C. 0,0942 D. 0,0342 21 C3-1-
Tỉ lệ thanh niên đã tốt nghiệp THPT của quận A B Nhóm 4 021
là 85%. Trong đợt tuyển quân đi nghĩa vụ quân
sự năm nay, quận A đã gọi ngẫu nhiên 32 thanh
niên. Tính xác suất để có từ 8 đến 14 thanh niên
bị loại do chưa tốt nghiệp THPT ? A. 13,79% B. 9,58% C. 26,32% D. 28,69% 22 C3-1-
Thống kê điểm thi X (điểm) môn XSTK của sinh D Nhóm 4 022
viên tại trường Đại học A cho thấy X là biến
ngẫu nhiên có quy luật phân phối chuẩn với giá
trị trung bình bằng 5,25 và độ lệch chuẩn bằng
1,25. Tỉ lệ sinh viên có điểm thi môn XSTK của
trường A từ 4 đến 6 điểm là: A. 56,71% B. 68,72% C. 64,72% D. 61,72% 23 C3-1-
Cho X ~B(10; 0,1). Khí đó giá trị P(1< X < 3) B Nhóm 4 023 bằng: A.0,29371 B. 0,19371 C. 0,39371 D.0,49371 24 C3-1-
Xác suất có bệnh của những người chờ khám D Nhóm 4 024
bệnh tại 1 bịnh viện là 72%. Khám lần lượt 61
người này, hỏi khả năng cao nhất có mấy người bị bệnh ? A. 41 người B. 42 người C. 43 người D. 44 người. 25 C3-1-
Một gia đình nuôi gà mái đẻ với xác suất đẻ C Nhóm 4 025
trứng của mỗi con gà trong 1 ngày là 0,75. Để
trung bình mỗi ngày có nhiều hơn 122 con gà
mái đẻ trứng thì số gà tối thiểu gia đình đó phải nuôi là: A. 151 con B. 162 con C. 163 con D. 175 con 26 C3-1-
Cho biến biến ngẫu nhiên X~ N(4; 2,25). Khi đó A Nhóm 4 026 P(X> 5,5) bằng: A.0,1587 B. 0,3413 C. 0,1916 D. 0,2707 27 C3-1-
Thời gian X (tháng) từ lúc vay đến lúc trả tiền A Nhóm 4 027
của 1 khách hàng tại ngân hàng A là biến ngẫu
nhiên có phân phối chuẩn: N(18; 16). Tỉ lệ
khách hàng trả tiền cho ngân hàng A sau 16 tháng ? A. 69,15% B. 59,63% C. 79,17% D. 49,63% 28 C3-1-
Tuổi thọ của sản phẩm là biến ngẫu nhiên phân C Nhóm 4 028
phối chuẩn với tuổi thọ trung bình là 4 năm và
độ lệch tiêu chuẩn là 1,5 năm. Thời gian bảo
hành sản phẩm được quy định là 3 năm. Tỷ lệ
sản phẩm phải bảo hành là: A. 15,14% B. 20,14% C. 25,14% D. 18,14% 29 C3-1-
Tuổi thọ của sản phẩm là biến ngẫu nhiên phân C Nhóm 4 029
phối chuẩn với tuổi thọ trung bình là 3 năm và
độ lệch tiêu chuẩn là 1,1 năm. Tỷ lệ sản phẩm hỏng trước 2,5 năm là: A. 28,82 % B. 23,82% C. 32,28% D. 38,22% 30 C7-1-
Trong bài toán kiểm định cho kỳ vọng của biến C Nhóm 5 030
ngẫu nhiên có phân phối chuẩn N(µ; σ ) (σ chưa 2
biết) với cặp giả thuyết: H : µ = µ 0 0 ; H : µ ≠ µ 1 0
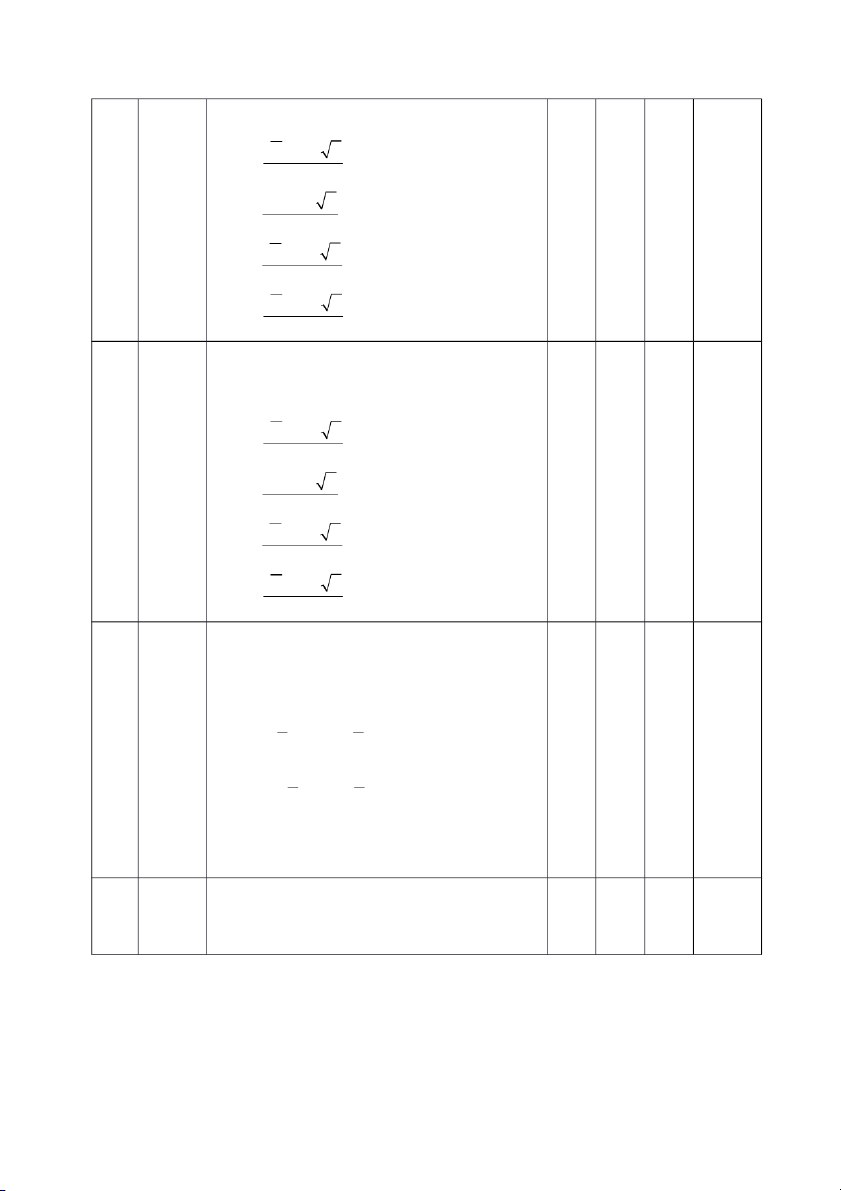
thì thống kê (tiêu chuẩn) kiểm định là: (X 0 ) n T A. (f 0 ) n T B. S (X 0 ) n T C. S (X 0 ) n T D. S 31 C7-1-
Trong bài toán kiểm định cho kỳ vọng của biến A Nhóm 5 031
ngẫu nhiên có phân phối chuẩn N(µ; σ ) (σ đã 2
biết) với cặp giả thuyết: H : µ = µ 0 0 ; H : µ < µ 1 0
thì thống kê (tiêu chuẩn) kiểm định là: (X 0 ) n T A. (f 0 ) n T B. S (X 0 ) n T C. (X 0 ) n T D. S 32 C7-1-
Trong bài toán kiểm định cho kỳ vọng của biến B Nhóm 5 032
ngẫu nhiên có phân phối chuẩn N(µ; σ ) (σ chưa 2
biết) với cặp giả thuyết: H : µ = µ 0 0 ; H : µ ≠ µ 1 0
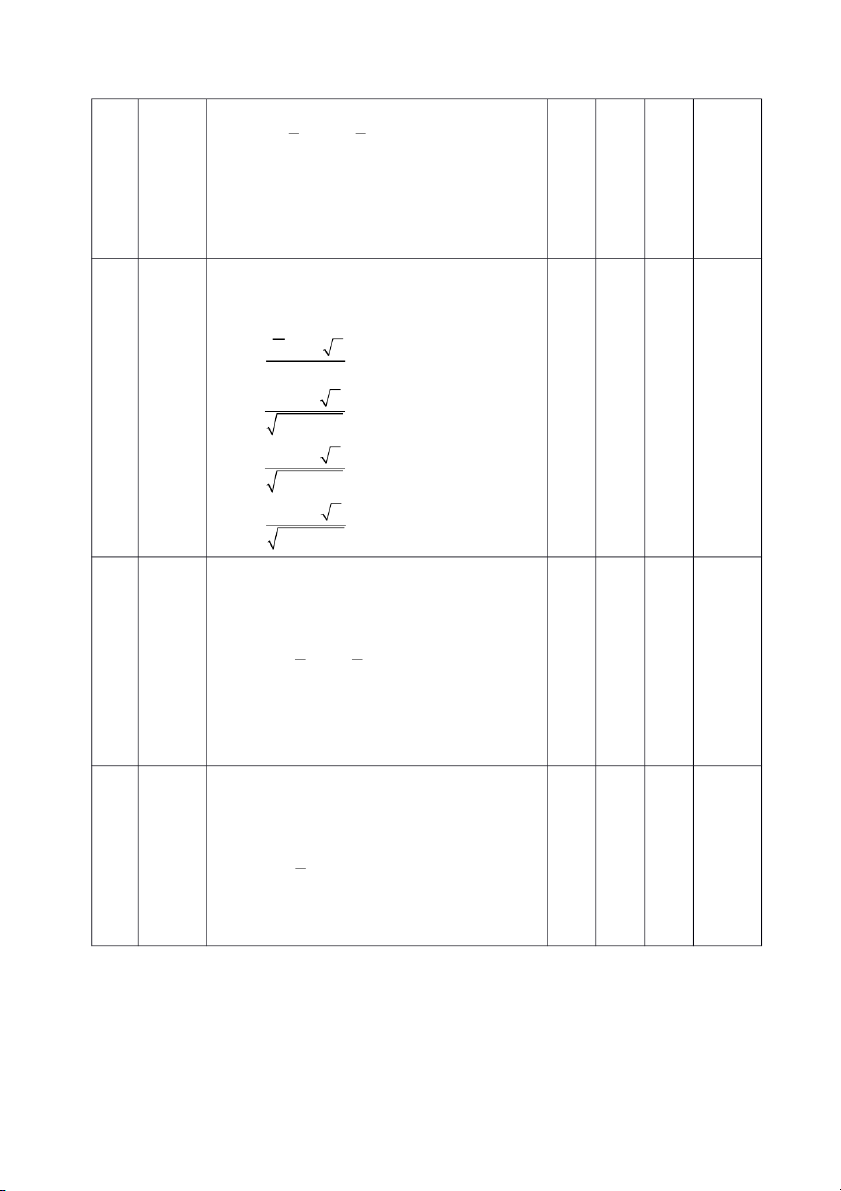
thì miền bác bỏ giả thuyết H là: 0 (n 1) (n 1) ( ; t ) ( t ; ) A. 2 2 (n 1) (n 1) ( ; t ) (t ; ) B. 2 2 (n 1) C. ( ; t ) (n 1) D. (t ; ) 33 C7-1-
Trong bài toán kiểm định cho kỳ vọng của biến D Nhóm 5 033
ngẫu nhiên có phân phối chuẩn N(µ; σ ) (σ chưa 2
biết) với cặp giả thuyết: H : µ = µ 0 0 ; H : µ > µ 1 0
thì miền bác bỏ giả thuyết H là: 0 (n 1) (n 1) ( ; t ) (t ; ) A. 2 2 (n 1) B. ( t ; ) (n 1) ( ; t ) C. (n 1) (t ; ) D. 34 C7-1-
Trong bài toán kiểm định cho tỷ lệ của tổng thể p B Nhóm 5 034
với kích thước mẫu n đủ lớn của cặp giả thuyết: H0 : p = p ; H 0 : p ≠ p 1
thì thống kê (tiêu chuẩn) 0 kiểm định là: (X 0 p ) n U A. (f p0) n U p (1 p ) B. 0 0 (f p0) n U C. p0(1 p0) (f p0) n U p (1p ) D. 0 0 35 C7-1-
Trong bài toán kiểm định cho tỷ lệ của tổng thể p A Nhóm 5 035
với kích thước mẫu n đủ lớn của cặp giả thuyết: H0 : p = p ; H 0 : p ≠ p 1
thì miền bác bỏ giả thuyết 0 H0 là:
( ; u ) ( u ; ) A. 2 2 B. ( ; u ) (u ; ) ( ; u ) C. (u ; ) D. 36 C7-1-
Trong bài toán kiểm định cho tỷ lệ của tổng thể p C Nhóm 5 036
với kích thước mẫu n đủ lớn của cặp giả thuyết: H0 : p = p ; H 0 : p < p 1
thì miền bác bỏ giả thuyết 0 H0 là: ( ; u ) A. 2 ( ; u ) (u ; ) B. ( ; u ) C. ( ; u ) D. 2 37 C1-2-
Trong một lớp học có 6 bóng đèn. Xác suất cháy B Nhóm 6 037
của mỗi bóng là 0,25. Lớp học đủ ánh sáng nếu
có ít nhất 4 bóng đèn sáng. Xác suất để lớp học không đủ ánh sáng là: A.17,95% B.16,95% C.18,95% D.19,95% 38 C1-2- C Nhóm 6 038
Có 3 người khách vào một trung tâm thương
mại, biết rằng khả năng để những người khách
này mua hàng tương ứng lần lượt là 0,6; 0,7 và
0,8. Tính xác suất để 3 người khách này đều mua hàng: A. 0,363 B. 0,633 C. 0,336 D. 0,233 39 C1-2- A Nhóm 6 039
Có 3 người khách vào một trung tâm thương
mại, biết rằng khả năng để những người khách
này mua hàng tương ứng lần lượt là 0,6; 0,7 và
0,8. Tính xác suất để 3 người khách này đều không mua hàng: A. 0,024 B. 0,24 C. 0,42 D. 0,204 40 C1-2- A Nhóm 6 040
Hai sinh viên cùng đi thi cuối kỳ môn toán. Xác
suất thi đỗ đối với từng sinh viên lần lượt là 0,72
và 0,8. Tính xác suất để có ít nhất một sinh viên thi đỗ: A. 0,944 B. 0,955 C. 0,966 D. 0,977 41 C1-2- D Nhóm 6 041
Hai sinh viên cùng đi thi cuối kỳ môn toán. Xác
suất thi đỗ đối với từng sinh viên lần lượt là 0,92
và 0,85. Tính xác suất để có đúng một trong hai sinh viên đó thi đỗ: A. 0,402 B. 0,306 C. 0,106 D. 0,206 42 C1-2-
Một công ty đầu tư 2 dự án A và B, dự án A đấu C Nhóm 6 042
thầu trước. Khả năng thắng thầu dự án A là
80% . Nếu dự án A thắng thầu thì khả năng thắng
thầu dự án B là 70% . Nếu dự án A không thắng
thầu thì khả năng thắng thầu dự án B là 60% .
Tìm xác suất để công ty thắng thầu ít nhất một dự án là: A. 0,75 B. 0,98 C. 0,92 D. 0,85 43 C1-2- A Nhóm 6 043
Xác suất để công ty A kinh doanh bị thua lỗ năm
tới là 0,2; công ty B kinh doanh bị thua lỗ năm
tới là 0,15; cả hai công ty trên đều thua lỗ năm
tới là 0,1. Xác suất để cả hai công ty trên đều
không bị thua lỗ trong năm tới là: A. 0,75 B. 0,57 C. 0,67 D. 0,76 44 C1-2- A Nhóm 6 044
Xác suất để công ty A kinh doanh bị thua lỗ năm
tới là 0,2; công ty B kinh doanh bị thua lỗ năm
tới là 0,15; cả hai công ty trên đều thua lỗ năm
tới là 0,1. Xác suất để có đúng một công ty kinh
doanh bị thua lỗ trong năm tới là: A. 0,15 B. 0,1 C. 0,2 D. 0,25 45 C1-2- C Nhóm 6 045
Một người đến công ty X để bán hàng 3 lần. Khả
năng lần đầu người đó bán được hàng là 0,8. Nếu
lần trước người đó bán được hàng thì khả năng để
lần tiếp theo bán được là 0,9; còn nếu lần trước
người đó không bán được thì khả năng để lần tiếp
theo bán được là 0,6. Tính xác suất để người đó
cả 3 lần đều bán được hàng là: A. 0,846 B. 0,468 C. 0,648 D. 0,486 46 C1-2-
Một trung tâm Tai–Mũi–Họng có tỉ lệ bịnh nhân D Nhóm 7 046
Tai, Mũi, Họng tương ứng là 25%, 40%, 35%; tỉ
lệ bệnh nặng phải mổ tương ứng là 1%, 2%, 3%.
Chọn ngẫu nhiên một bệnh nhân từ trung tâm
này thì được người bị mổ. Xác suất để người
được chọn bị bệnh về Họng là: A. 0,6 B. 0,4 C. 0,5 D. 0,3 47 C1-2-
Một trung tâm Tai–Mũi–Họng có tỉ lệ bệnh nhân B Nhóm 7 047
Tai, Mũi, Họng tương ứng là 25%, 40%, 35%; tỉ
lệ bệnh nặng phải mổ tương ứng là 1%, 2%, 3%.
Xác suất để chọn ngẫu nhiên được một bệnh
nhân phải mổ từ trung tâm này là: A. 0,008 B.0,021 C. 0,312 D. 0,381 48 C1-2-
Một trung tâm Tai–Mũi–Họng có tỉ lệ bệnh nhân D Nhóm 7 048
Tai, Mũi, Họng tương ứng là 25%, 40%, 35%; tỉ
lệ bệnh nặng phải mổ tương ứng là 1%, 2%, 3%.
Chọn ngẫu nhiên một bệnh nhân từ trung tâm
này thì được người bị mổ. Xác suất để người
được chọn bị bệnh Mũi là: A. 0,008 B. 0,021 C. 0,312 D.0,381 49 C1-2- C Nhóm 7 049
Một cửa hàng điện máy nhập lô hàng bao gồm: 8
sản phẩm loại 1; 7 sản phẩm loại 2 và 5 sản
phẩm loại 3. Biết rằng xác suất để mỗi sản phẩm
loại 1, 2, 3 tương ứng bị hỏng trong quá trình
vận chuyển là 1%; 1,5% và 1,8%. Sau khi lô
hàng đó vận chuyển về kho của cửa hàng, người
ta lấy ra ngẫu nhiên 1 sản phẩm để kiểm tra. Xác
suất để sản phẩm lấy ra này bị hỏng là: A. 0,05317 B. 0,03157 C. 0,01375 D. 0,07315 50 C1-2- A Nhóm 7 050
Tỷ lệ sinh viên nữ ở một trường đại học là 75%.
Biết rằng, trong số sinh viên nữ, tỷ lệ sinh viên
có học lực giỏi là 28%; còn trong số sinh viên
nam, tỷ lệ sinh viên có học lực giỏi là 20%. Xác
suất để khi chọn ngẫu nhiên một sinh viên ở
trường đó thì được sinh viên có học lực giỏi: A. 0,26 B. 0,46 C. 0,36 D. 0,16 51 C1-2-
Một nhà máy có ba phân xưởng I,II,và III cùng C Nhóm 7 051
sản xuất ra một loại sản phẩm. Phân xưởng
I,II,III sản xuất tương ứng 40%,35%, 25% sản
lượng của nhà máy với tỷ lệ phế phẩm tương
ứng là 0,12 ; 0,1 ; 0,08. Tìm tỷ lệ phế phẩm chung của nhà máy là: A. 0,303 B. 0,203 C. 0,103 D. 0,403 52 C8-2-
Năng suất lúa là một biến ngẫu nhiên có phân A Nhóm 8 052
phối chuẩn. Năng suất lúa trung bình của vụ
trước là 55 tạ/ha. Vụ lúa năm nay người ta áp
dụng phương pháp kỹ thuật mới cho toàn bộ diện
tích trồng lúa trong vùng. Điều tra 100ha thu
được năng suất trung bình là 57,5 tạ/ha và độ
lệch chuẩn là 8,3182 tạ/ha. Với mức ý nghĩa 5%
thì giá trị thống kê kiểm định ý kiến: “Phương
pháp mới làm tăng năng suất lúa của địa phương” là: A. Tqs = 3,0055 B. Tqs = 3,5050 C. Tqs = 3,5500 D. Tqs = 3,5055 53 C8-2-
Trọng lượng của sản phẩm là biến ngẫu nhiên A Nhóm 8 053
tuân theo quy luật phân phối chuẩn. Trọng lượng
của sản phẩm theo quy định là 6kg. Sau một thời
gian sản xuất người ta tiến hành kiểm tra 121 sản
phẩm thu được trọng lượng trung bình là
5,975kg và độ lệch chuẩn là 2,399kg. Sản xuất
được gọi là bình thường nếu trọng lượng sản
phẩm bằng trọng lượng quy định. Với mức ý
nghĩa 5%, hãy cho biết kết luận nào dưới đây là đúng:
A. Sản xuất là bình thường.
B. Sản xuất không bình thường.
C. Chưa thể có kết luận gì về tình hình sản xuất.
D. Cả ba đáp án đều sai. 54 C8-2-
Năng suất lúa là một biến ngẫu nhiên có phân A Nhóm 8 054
phối chuẩn. Năng suất lúa trung bình mọi vụ
trước là 55,5 tạ/ha. Vụ lúa năm nay người ta áp
dụng phương pháp kỹ thuật mới cho toàn bộ diện
tích trồng lúa trong vùng. Điều tra 100ha thu
được năng suất trung bình là 57,7 tạ/ha và độ
lệch chuẩn là 8,2765 tạ/ha. Với mức ý nghĩa 5%,
hãy cho biết khẳng định nào sau đay là đúng:
A. Phương pháp mới làm tăng năng suất lúa của địa phương.
B. Phương pháp mới làm giảm năng suất lúa của địa phương.
C. Phương pháp mới không làm thay đổi
năng suất lúa của địa phương.
D. Cả ba đáp án đều sai. 55 C7-2-
Trọng lượng của sản phẩm là biến ngẫu nhiên B Nhóm 9 055
tuân theo quy luật phân phối chuẩn. Người ta
tiến hành kiểm tra 121 sản phẩm thu được trọng
lượng trung bình là 5,975kg và độ lệch chuẩn là
2,399kg. Với độ tin cậy 95%, khoảng tin cậy của
trọng lượng trung bình của sản phẩm là: A. (5,892 ; 6,673) B. (5,548 ; 6,402) C. (5,821 ; 6,578) D. (5,121 ; 6,513) 56 C7-2- D Nhóm 9 056
Doanh thu hàng tháng của các đại lý này là đại
lượng ngẫu nhiên có phân phối chuẩn. Điều tra
ngẫu nhiên doanh thu (tỷ đồng/tháng) của 26 đại
lý kinh doanh sữa bột cho trẻ em tại một thành
phố của Việt Nam thu được doanh thu trung bình
là 8,23 tỷ/tháng và độ lệch chuẩn là 0,5427. Với
độ tin cậy 0,95 hãy ước lượng doanh thu bình
quân hàng tháng của các đại lý bán sữa bột cho
trẻ em tại thành phố đó: A. (8,315 ; 8,781) B. (8,254 ; 8,912) C. (7,823 ; 8,342 ) D. (8,011 ; 8,449) 57 C7-2- A Nhóm 9 057
Chiều cao của mỗi cây xoài giống Thái Lan sau
6 tháng trồng ở một nhà vườn xem như là đại
lượng ngẫu nhiên tuân theo quy luật phân phối
chuẩn. Chọn một mẫu gồm 25 cây tại nhà vườn
đó để đo chiều cao và tính được chiều cao trung
bình là 163 cm và độ lệch chuẩn là 3,2 cm. Với
độ tin cậy 90%, hãy xác định khoảng tin cậy khi
ước lượng chiều cao trung bình của toàn bộ các
cây xoài giống Thái Lan được trồng tại nhà vườn đó: A. ( 161,67 cm ; 164,32 cm) B. ( 162,67 cm ; 166,95 cm) C. ( 151,67 cm ; 171,95 cm) D. (154,05 cm ; 174,95 cm) 58 C7-2- C Nhóm 9 058
Cho X là khối lượng của một loại sản phẩm, 2 X ~ N( ;
). Cân thử 25 sản phẩm loại đó
thấy khối lượng trung bình là 126 gam và độ
lệch tiêu chuẩn là 17gam. Với độ tin cậy 95%,
hãy cho biết trọng lượng trung bình tối đa của sản phẩm là bao nhiêu? A. 129,382 kg B. 130,421 kg C. 131,936 kg D. 134,951 kg 59 C7-2- A Nhóm 9 059
Cho X là khối lượng của một loại sản phẩm, 2 X ~ N( ;
). Cân thử 25 sản phẩm loại đó
thấy khối lượng trung bình là 126 gam và độ
lệch tiêu chuẩn là 17gam. Với độ tin cậy 95%,
hãy cho biết trọng lượng trung bình tối thiểu của sản phẩm là bao nhiêu? A. 120,06 kg B. 123,06 kg C. 119,06 kg D. 122,06 kg 60 C7-2- A Nhóm 9 060
Trong 180 hộ gia đình được chọn ngẫu nhiên ở
một vùng thấy có 144 hộ gia đình có sử dụng
Internet. Với độ tin cậy 0,95 hãy ước lượng tỷ lệ
hộ gia đình có sử dụng Internet ở vùng đó: A. (74,16% ; 85,84%) B. (72,16% ; 81,84%) C. (73,16% ; 82,84%) D. (70,16% ; 83,84%) 61 C7-2- C Nhóm 9 061
Chọn ngẫu nhiên 200 công nhân ở một khu công
nghiệp thấy thu nhập (triệu đồng/tháng) của họ
thấy có 82 công nhân có mức thu nhập tối thiểu
8,6 triệu/tháng (công nhân có mức thu nhập
khá). Với độ tin cậy 92%, tỷ lệ công nhân có thu
nhập khá nằm trong khoảng nào: A. (36,91% ; 49,09%) B. (37,91% ; 48,09%) C. (34,91% ; 47,09%) D. (35,91% ; 49,09%) 62 C2-3- B Nhóm 062
Tỷ lệ người mắc bệnh viêm gam B ở một địa 10
phương năm trước là 10%. Năm nay, khám sức
khỏe ngẫu nhiên 400 người dân ở địa phương đó
thấy có 28 người mắc bệnh viêm gam B. Với
mức ý nghĩa 2,5% có thể cho rằng tỷ lệ người
mắc bệnh viêm gam B năm nay ở địa phương
này giảm xuống hay không?
A. Tỷ lệ người mắc bệnh viêm gam B năm
nay ở địa phương này không giảm xuống.
B. Tỷ lệ người mắc bệnh viêm gam B năm
nay ở địa phương này giảm xuống.
C. Tỷ lệ người mắc bệnh viêm gam B năm
nay ở địa phương này không thay đổi.
D. Chưa thể biết được. 63 C2-3-
Số lượng xe ô tô TOYOTA (ký hiệu là X) mà D Nhóm 063
một đại lý bán được trong một tuần có bảng phân 10 phôi xác suất như sau: X 0 1 2 P 0,05 0,13 0,12
Giả sử giá bán 500 triệu/xe. Chi phí cố định là
900 triệu/tuần và giá nhập xe là 400 triệu/xe.
Tìm xác suất để đại lý có lãi của đại lý mỗi tuần. A. 0,32 B. 0,39 C. 0,07 D. 0,35 64 C2-3-
Số lượng xe ô tô (ký hiệu là X) mà một đại lý C C Nhóm 064
bán được trong một tuần có bảng phân phôi xác 10 suất như sau: X 0 1 2 P 0,05 0,13 0,12
Giả sử giá bán 500 triệu/xe và tổng chi phí là
1,2tỷ/tuần. Xác suất để đại lý có lãi là: A. 0,92 B. 0,82 C. 0,7 D. 0,8 65 C2-3-
Số lượng xe ô tô (ký hiệu là X) mà một đại lý A Nhóm 065
bán được trong một tuần có bảng phân phôi xác 10 suất như sau: X 0 1 2 P 0,05 0,13 0,12
Giả sử giá bán 500 triệu/xe. Chi phí cố định là
250 triệu/tuần và giá nhập xe là 400 triệu/xe.
Xác suất để đại lý bị thua lỗ là: A. 30% B. 65% C. 18% D. 35% 66 C2-3-
Theo thống kê trung bình cứ 1.000 người dân ở C Nhóm 066
độ tuổi 40 thì sau 1 năm có 996 người còn sống. 10
Một công ty bảo hiểm nhân thọ bán bảo hiểm 1
năm cho những người ởđộ tuổi này với giá 1,5
triệu đồng, nếu người mua bảo hiểm chết thì số
tiền bồi thường là 300 triệu đồng. Giả sử công ty
bán được 40.000 hợp đồng bảo hiểm loại này
(mỗi hợp đồng ứng với 1 người mua bảo hiểm)
trong 1 năm. Hỏi trong 1 năm lợi nhuận trung
bình thu được của công ty về loại bảo hiểm này là bao nhiêu ? A. 1,2 tỉđồng B. 1,5 tỉđồng C. 12 tỉđồng D. 15 tỉđồng 67 C2-3-
Theo thống kê trung bình cứ 1.000 người đi xe D Nhóm 067
máy thì có 25 người bị tai nạn trong 1 năm. Một 10
công ty bảo hiểm bán bảo hiểm loại này cho
20.000 người trong 1 năm với giá 98 ngàn đồng
và mức chi trả khi bị tai nạn là 3 triệu đồng. Hỏi
trong 1 năm lợi nhuận trung bình thu được của
công ty về loại bảo hiểm này là bao nhiêu ? A. 445 triệu đồng B. 450 triệu đồng C. 455 triệu đồng D. 460 triệu đồng 68 C2-3-
Một cửa hàng điện máy bán 1 chiếc máy lạnh A D Nhóm 068
thì lời 850.000 đồng nhưng nếu chiếc máy lạnh 10
đó phải bảo hành thì lỗ 1.000.000 đồng. Biết xác
suất máy lạnh A phải bảo hành của cửa hàng là
15%, tính mức lời trung bình khi bán 1 chiếc máy lạnh A ? A. 722.500đồng B. 675.500đồng C. 605.500đồng D. 572.500đồng 69 C2-3-
Một cửa hàng điện máy bán 1 chiếc tivi thì lời B Nhóm 069
500.000 đồng nhưng nếu chiếc tivi đó phải bảo 10
hành thì lỗ 700.000 đồng. Tính xác suất tivi phải
bảo hành của cửa hàng để mức lời trung bình khi
bán 1 chiếc tivi là 356.000 đồng ? A. 10% B.12% C. 15% D. 23% 70 C1-3- D Nhóm 070
Một người đến công ty X để bán hàng 3 lần. Khả 10
năng lần đầu người đó bán được hàng là 0,8. Nếu
lần trước người đó bán được hàng thì khả năng để
lần tiếp theo bán được là 0,9; còn nếu lần trước
người đó không bán được thì khả năng để lần tiếp
theo bán được là 0,6. Tính xác suất để người đó
có đúng 2 lần bán được hàng là: A. 0,868 B. 0,288 C. 0,882 D. 0,828
Hà Nội, ngày 20 tháng 6 năm 2021 Phó trưởng khoa TS. Đàm Thanh Tú



