Đề thi thử môn Toán theo cấu trúc đề minh họa 2021 - Đề 2 (có lời giải và đáp án)
Đề thi thử môn Toán theo cấu trúc đề minh họa 2021 - Đề 2 có lời giải và đáp án. Tài liệu được biên soạn dưới dạng file PDF bao gồm 20 trang tổng hợp các kiến thức tổng hợp giúp các bạn tham khảo, ôn tập và đạt kết quả cao trong kỳ thi sắp tới. Mời các bạn đón xem!
Chủ đề: Đề thi THPTQG môn Toán năm 2021 60 tài liệu
Môn: Toán 2.2 K tài liệu
Tác giả:
Preview text:
ĐỀ THI THỬ CHUẨN CẤU
KỲ THI TỐT NGHIỆP TRUNG HỌC PHỔ THÔNG NĂM 2021 TRÚC MINH HỌA Bài thi: TOÁN ĐỀ SỐ 02
Thời gian làm bài: 90 phút không kể thời gian phát đề
(Đề thi có 08 trang)
Họ, tên thí sinh: …………………………………………………
Số báo danh: …………………………………………………….
Câu 1: Tập hợp M có 12 phần tử. Số tập con gồm 2 phần tử của M là A. 2 12 . B. 2 C . C. 10 A . D. 2 A . 12 12 12
Câu 2: Cho cấp số cộng (u có u = 12
− và u =18. Giá trị công sai của cấp số cộng đó là n ) 4 14 A. d = 4. B. d = 3. − C. d = 3. D. d = 2. −
Câu 3: Cho đường thẳng a song song với mặt phẳng (P). Có bao nhiêu mặt phẳng chứa a và vuông góc với (P)? A. Không có B. Có một C. Có vô số
D. Có một hoặc vô số
Câu 4: Cho hàm số f ( x) có bảng biến thiên như hình vẽ. x − 1 3 + f '( x) + 0 − 0 + f ( x) 1 − + − −3
Điểm cực đại của hàm số đã cho là: A. x = 3. −
B. x = 3. C. x = 1. −
D. x = 1. x +
Câu 5: Tiệm cận ngang của đồ thị hàm số 2 1 y = l là x −1 1 A. y = 1. −
B. y = 1. C. y = .
D. y = 2. 2
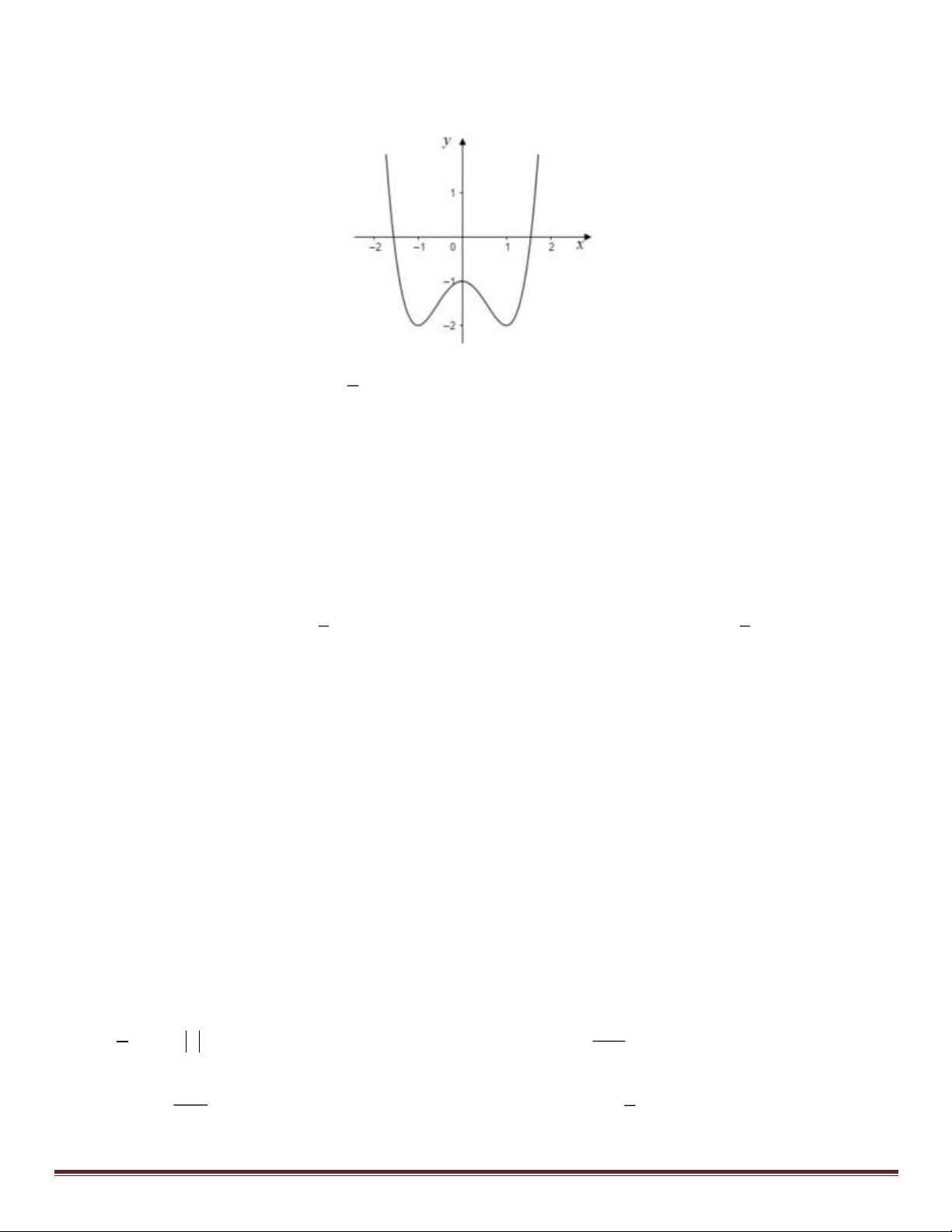
Câu 6: Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình bên? A. 4 2
y = −x + 2x . B. 2
y = x − 2x +1. Trang 1 C. 3
y = x − 3x +1. D. 3
y = −x + 3x +1.
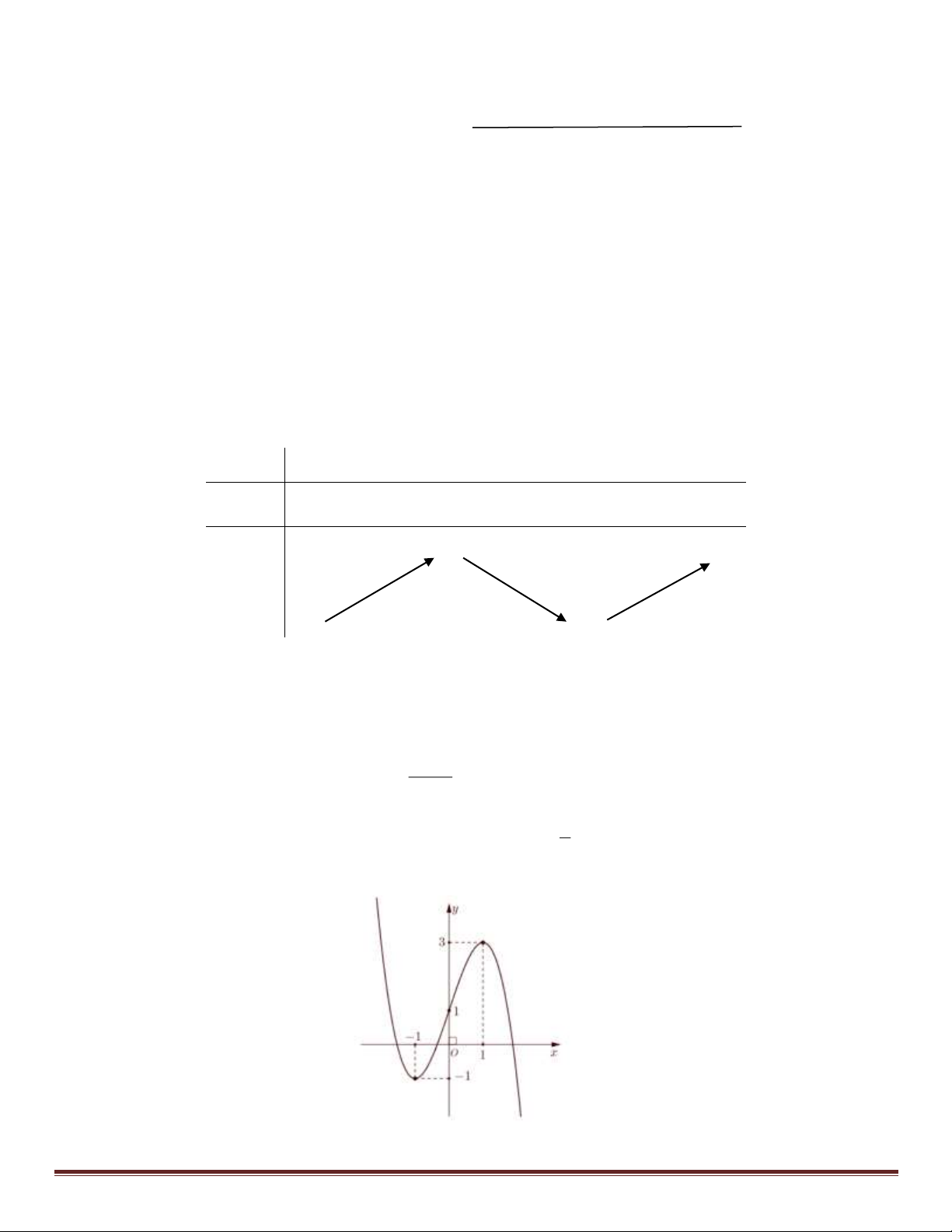
Câu 7: Cho hàm số bậc bốn y = f ( x) có đồ thị là đường cong trong hình bên.
Số nghiệm của phương trình f (x) 1 = − là 2 A. 2. B. 3. C. 4.
D. x = 1.
Câu 8: Cho hai số phức z = 5i và z = 2020 + .
i Phần thực của số z z bằng 1 2 1 2 A. 5. − B. 5. C. 10100. − D. 10100. 1 Câu 9: 3x 1 e + dx bằng 0 1 1 A. 3 e − . e B. ( 4 e + e). C. 4 e − . e D. ( 4
e − e). 3 3
Câu 10: Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P) : x − 2y + z − 5 = 0 . Điểm nào dưới đây thuộc ( P)? A. M (1;1;6). B. N ( 5 − ;0;0).
C. P (0;0 − 5). D. Q (2; 1 − ;5).
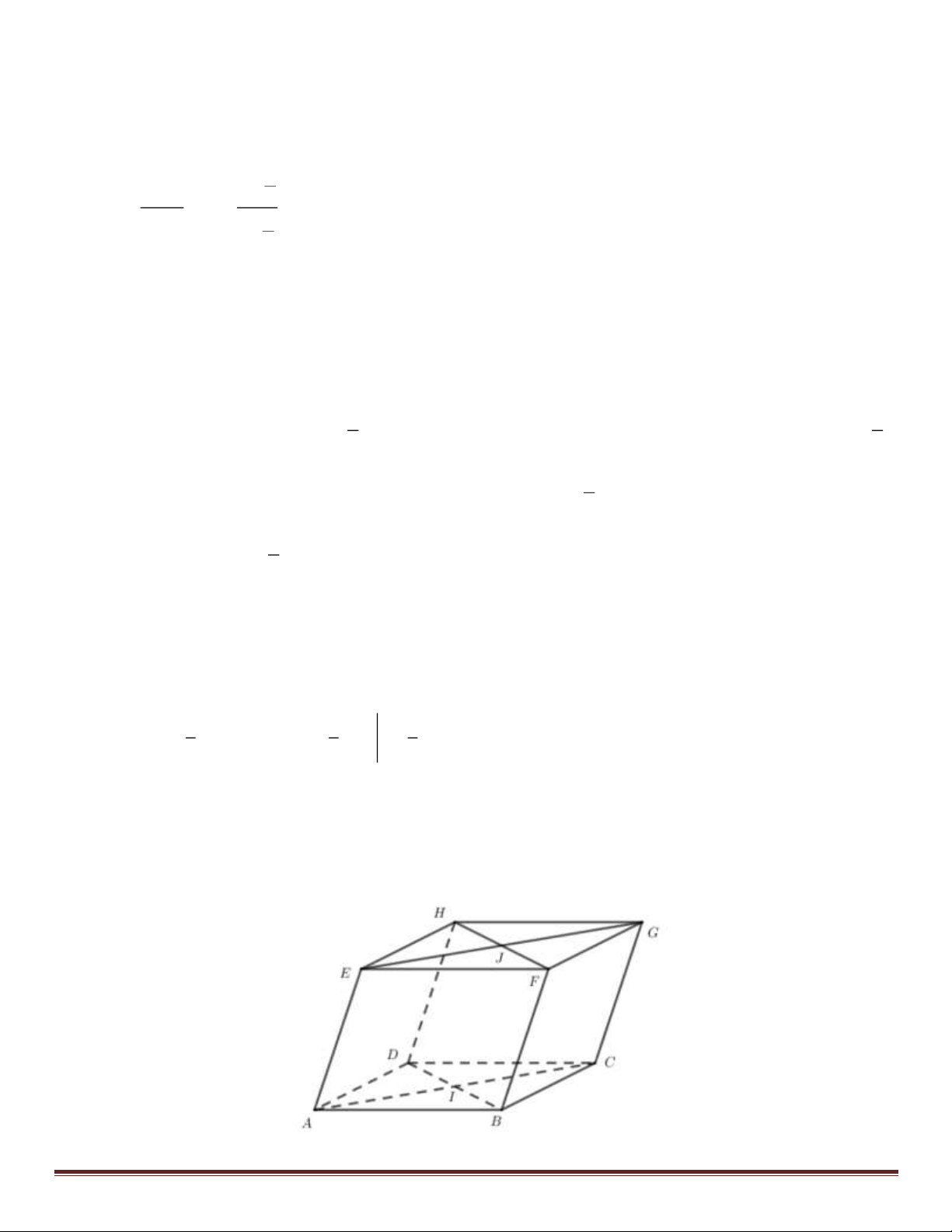
Câu 11: Cho hình hộp ABC .
D EFGH. Gọi I , J lần lượt là tâm của hình bình hành ABCD và EFGH. Khẳng
định nào sau đây là sai?
A. ( ABCD) // (EFGH ).
B. ( ABJ ) // (GHI ).
C. ( ACGE) // (BDHF ).
D. ( ABFE) // (DCGH ).
Câu 12: Cho khối chóp có diện tích đáy 2
B = 6a và chiều cao h = 2 .
a Thể tích khối chóp đã cho bằng: A. 3 12a . B. 3 2a . C. 3 4a . D. 3 6a .
Câu 13: Trong các khẳng định sau, khẳng định nào sai? + 1 e 1 x A. dx = ln x + . C B. e x dx = + C. x e +1 x 1 e + 1 C. x e dx = + C. D. cos 2xdx = sin 2x + C. x +1 2 Trang 2
Câu 14: Trong không gian Oxyz, cho a = ( 2
− ;2;0),b = (2;2;0),c = (2;2;2). Giá trị của a +b + c bằng A. 2 6. B. 11. C. 2 11. D. 6. −
Câu 15: Phương trình 2 x 2 3 x = 1 có nghiệm là
A. x = 0; x = 2. B. x = 1 − ; x = 3.
C. x = 0; x = 2 − .
D. x =1; x = 3 − . x − y + z −
Câu 16: Trong không gian Oxyz, cho đường thẳng 3 1 5 d : = =
. Vectơ sau đây là một vectơ chỉ 2 2 − 3
phương của đường thẳng d ? A. u = 1; 2 − ;3 . B. u = 2 − ; 4 − ;6 . 4 ( ) 2 ( ) C. u = 2;6; 4 − . D. u = 3; 1 − ;5 . 1 ( ) 3 ( )
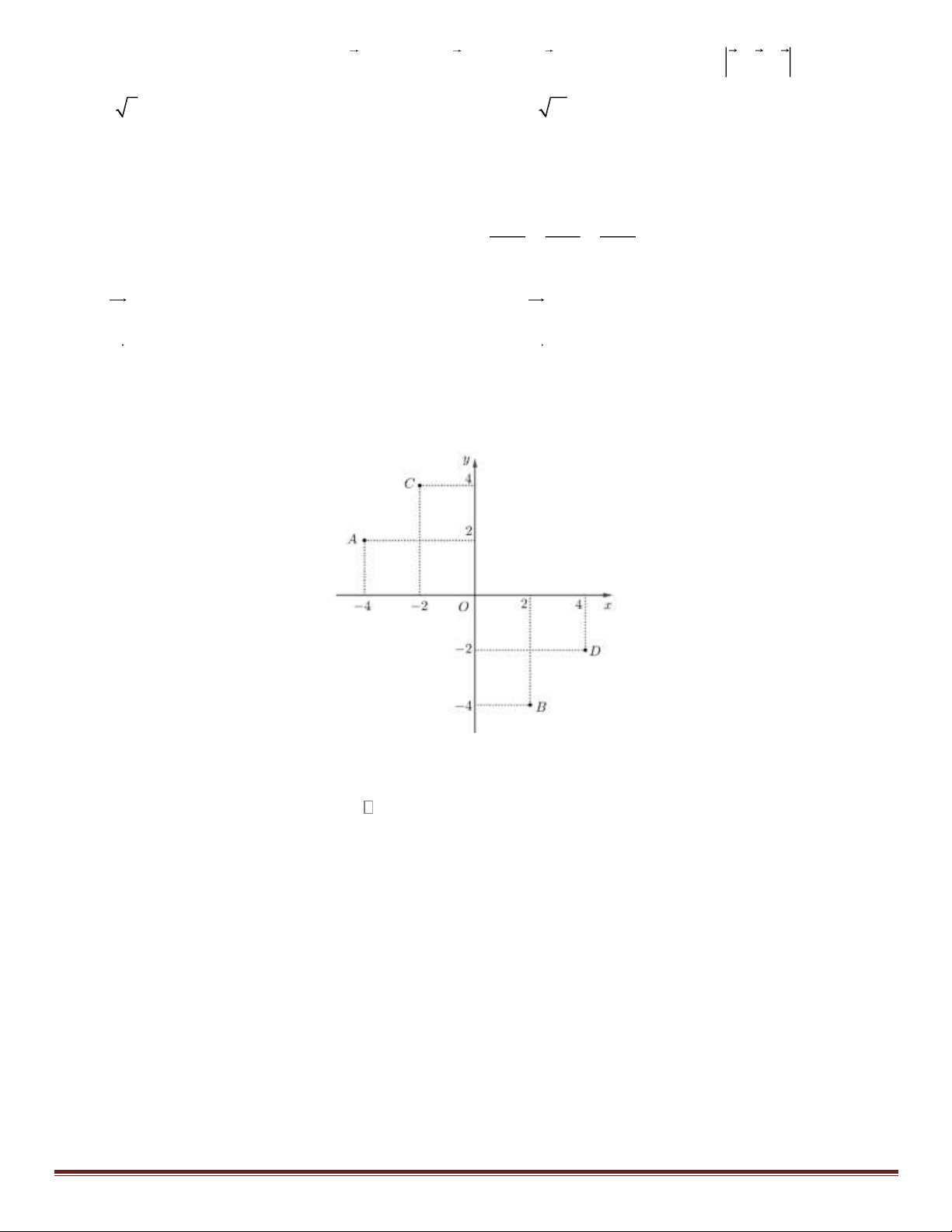
Câu 17: Trog mặt phẳng Ox ,
y số phức z = 2
− + 4i được biểu diễn bởi điểm nào trong các điểm ở hình vẽ duới đây?
A. Điểm C. B. Điểm . D C. Điểm . A D. Điểm . B 1 3 3
Câu 18: Cho hàm số f ( x) liên tục trên và thỏa mãn f
(x)dx = 2; f
(x)dx = 6. Tính I = f (x)dx . 0 1 0
A. I = 8.
B. I = 12.
C. I = 4.
D. I = 36.
Câu 19: Khối nón có chiều cao h = 4 và đường kính đáy bằng 6. Thể tích khối nón bằng A. 12 . B. 144 . C. 48. D. 24.
Câu 20: Cho khối hộp hình chữ nhật có ba kích thước 2;4;6. Thể tích của khối hộp đã cho bằng A. 8. B. 16. C. 48. D. 12.
Câu 21: Cho hai số phức z = 1− 2i và z = 2 + .
i Số phức z + z bằng 1 2 1 2 A. 3 − − .i B. 3 + . i C. 3 − . i D. 3 − + .i
Câu 22: Trong không gian Oxyz, cho mặt cầu (S ) 2 2 2
: x + y + z − 4x + 2y − 6z +1 = 0 . Tọa độ tâm I của mặt cầu là Trang 3 A. I (4; 2 − ;6). B. I (2; 1 − ;3). C. I ( 4 − ;2; 6 − ). D. I ( 2 − ;1;− ) 3 .
Câu 23: Cho hàm số y = f ( x) có bảng biến thiên như sau: x ' − 1 − 0 1 + y ' + 0 − − 0 + y 2 + + − − 4
Hàm số nghịch biến trong khoảng nào? A. (0 ) ;1 . B. ( 1 − ; ) 1 . C. (4;+). D. ( ; − 2).
Câu 24: Nghiệm của phương trình log x + 9 = 5 là 2 ( ) A. x = 41. B. x = 16. C. x = 23. D. x = 1. Câu 25: Cho ,
x y 0 và , . Khẳng định nào sau đây sai ? A. (
x ) = x .
B. x + y = ( x + y) . +
C. x .x = x . D. (
xy ) = x .y .
Câu 26: Cho hình trụ có bán kính đáy r = 2 và chiều cao h = 5. Diện tích xung quanh của hình trụ đã cho bằng A. 28. B. 20. C. 10 . D. 20.
Câu 27: Trong không gian Oxyz, cho các điểm A(1;0;2), B(1;2; )
1 ,C (3;2;0) và D(1;1;3). Đường thẳng đi
qua A và vuông góc với mặt phẳng ( BCD) có phương trình là x = 1− t x = 1+ t x = 1− t x = 2 + t
A. y = 4t . B. y = 4 .
C. y = 2 − 4t .
D. y = 4 + 4t . z = 2 + 2t z = 2 + 2t z = 2 − 2t z = 4 + 2t 3 1 + 2− 3 a .a
Câu 28: Rút gọn biểu thức P = ( với a 0. + a − ) 2 2 2 2 A. 4 P = a . B. 3 P = a . C. 5 P = a . D. P = . a 1 1 1 Câu 29: Cho f
(x)dx = 2 và g
(x)dx = 5. Tính ( f (x)−2g(x))dx. 0 0 0 A. 8. − B. 12. C. 1. D. 3. − Câu 30: Cho 2 f ( )
x = 3x + (1− 2 )
m x + 2m với m là tham số. Tìm m để F(x) là một nguyên hàm của f (x) và
F(0) = 3, F(1) = 3 − . Trang 4 5 15 15 1 A. m = − . B. m = . C. m = − . D. m = − . 2 2 2 2 x
Câu 31: Nghiệm của bất phương trình 2 log x log + 4 là: 2 2 4 1 1 A. x 0 . B. x 4 . C. 0 x . D. 0; 4;+ ) . 2 2
Câu 32: Một em bé có bộ 6 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 3 thẻ chữ T, một thẻ chữ N,
một thẻ chữ H và một thẻ chữ P. Em bé đó xếp ngẫu nhiên 6 thẻ đó thành một hàng ngang. Tính xác suất em bé
xếp được thành dãy TNTHPT. 1 1 1 1 A. . B. . C. . D. . 120 720 6 20
Câu 33: Tính (x − sin 2x) . dx cos 2x 2 x cos 2x A. 2 x + + C. B. + + C. 2 2 2 2 x 2 x C. + cos 2x + C. D. + sin x + C. 2 2
Câu 34: Cho số phức z thỏa mãn điều kiện (1+ i) z −1− 3i = 0. Tìm phần ảo của số phức w =1− iz + . z A. 1. − B. . i − C. 2. D. 2 − .i
Câu 35: Trong không gian Oxyz, cho hai điểm I (1;1; )
1 và A(1;2;3). Phương trình mặt cầu có tâm I và đi qua A là 2 2 2 2 2 2 A. ( x + ) 1 + ( y + ) 1 + ( z + ) 1 = 29. B. ( x − ) 1 + ( y − ) 1 + ( z − ) 1 = 25. 2 2 2 2 2 2 C. ( x − ) 1 + ( y − ) 1 + ( z − ) 1 = 5. D. ( x + ) 1 + ( y + ) 1 + ( z + ) 1 = 5. 2 2 x −3x−7 1 −
Câu 36: Số nghiệm nguyên của bất phương trình 2 x 21 3 là 3 A. 7. B. 6. C. vô số. D. 8. 2
Câu 37: Hàm số y =
nghịch biến trên khoảng nào dưới đây? 2 3x +1 A. ( 1 − ; ) 1 . B. ( ; − 0). C. (− ; +). D. (0;+).
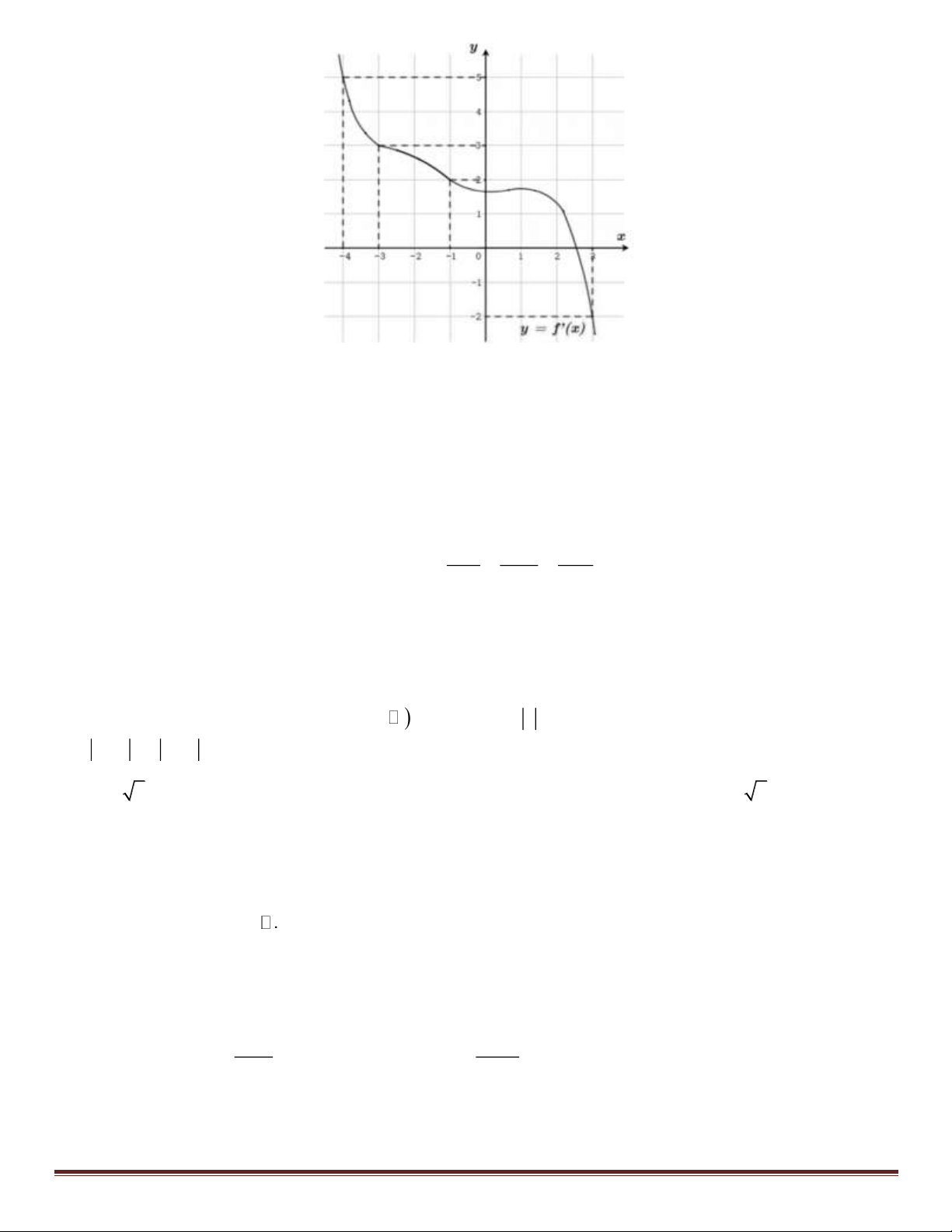
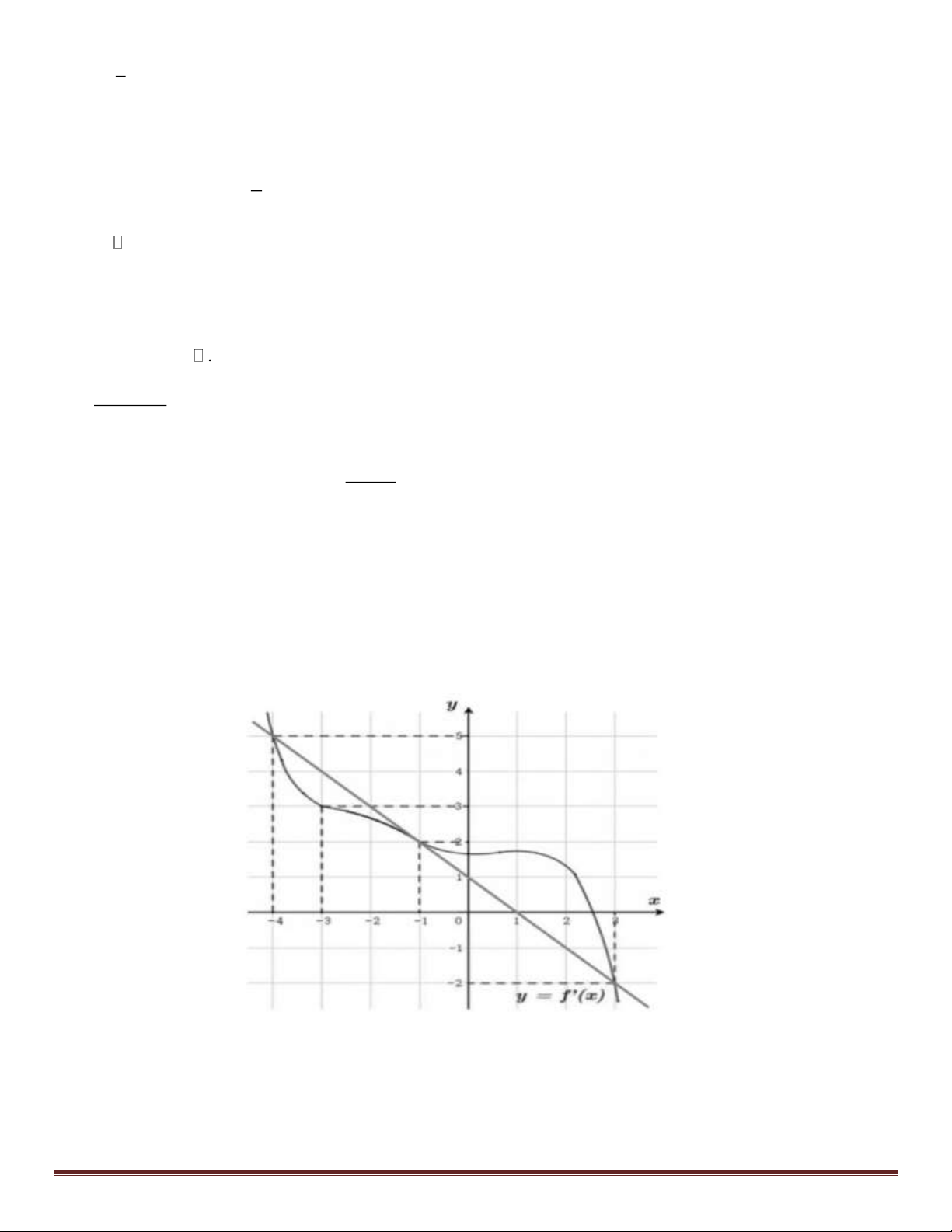
Câu 38: Cho hàm số f ( x). Biết hàm số f '( x) có đồ thị như hình dưới đây. Trên 4 − ; 3 , hàm số
g ( x) = f ( x) + ( − x)2 2 1
đạt giá trị nhỏ nhất tại điểm nào? Trang 5 A. x = 1. − B. x = 3. C. x = 4. − D. x = 3. −
Câu 39: Người ta muốn xây bể chứa nước dạng hình hộp chữ nhật không nắp có thể tích 3 200 m . Đáy bể là
hình chữ nhật có chiều dài gấp đôi chiều rộng. Giá thuê công nhân xây bể là 300.000 đồng/ 2 m . Chi phí thuê công nhân thấp nhất là A. 36 triệu đồng. B. 51 triệu đồng. C. 75 triệu đồng. D. 46 triệu đồng.
Câu 40: Trong không gian Oxyz, đường thẳng đi qua điểm M (1;2;2), song song với mặt phẳng ( x − y − z −
P) : x − y + z + 3 = 0 đồng thời cắt đường thẳng 1 2 3 d : = = có phương trình là 1 1 1 x =1− t x = 1+ t x = 1− t x = 1− t
A. y = 2 + t .
B. y = 2 − t .
C. y = 2 − t .
D. y = 2 − t . z = 2 z = 2 z = 2 − t z = 2
Câu 41: Cho số phức z = a + bi ( ,
a b ) thỏa mãn z =1. Tìm giá trị lớn nhất của biểu thức
A = z + 2 + 2 z − 2 . A.10 2. B. 7 C.10 D. 5 2
Câu 42: Cho hàm số f ( x) xác định và có đạo hàm f '( x) liên tục trên đoạn 1;
3 và f ( x) 0 với mọi x 1; 3 , đồng thời
f ( x) + ( + f ( x)) = ( f ( x)) (x − ) 2 2 2 ' 1 1 và f ( ) 1 = 1 − . Biết rằng 3 f
(x)dx = aln3+ ,ba,b . Tính tổng 2
S = a + b . 1 A. S = 1. − B. S = 2. C. S = 0. D. S = 4. − Câu 43: Có bao nhiêu bộ ( ;x y) với , x y nguyên và 1 , x y 2020 thỏa mãn ( +
xy + x + y + ) 2 y 2x 1 2 4 8 log
2x + 3y − xy − 6 log ? 3 ( ) 2 y + 2 x − 3 A. 4034. B. 2 . C. 2017 . D. 2017 2020 .
Câu 44: Đường cong 4 2 2
y = x − 2m x +1 có ba điểm cực trị A,B,C lập thành một tam giác đều. Giá trị của m là: Trang 6 A. 3 . B. 6 3 . C. 5 2 . D. 5 7 .
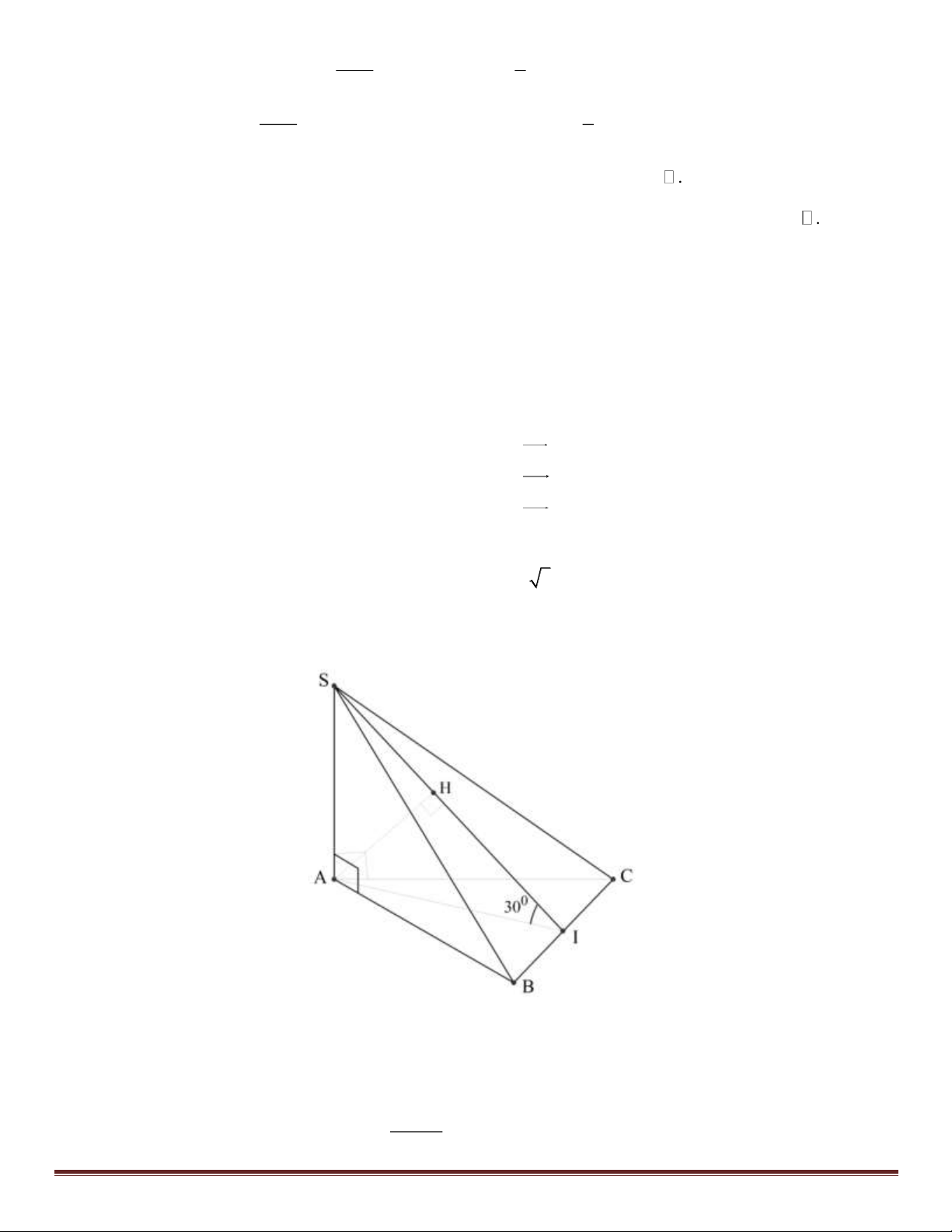
Câu 45: Cho hình chóp S.ABC có đáy ABC là tam giác đều, SA ⊥ ( ABC). Mặt phẳng (SBC) cách A một
khoảng bằng a và hợp với mặt phẳng ( ABC) góc 0
30 . Thể tích của khối chóp S.ABC bằng 3 8a 3 3a 3 4a 3 8a A. . B. . C. D. . 9 12 9 3
Câu 46: Cho hàm số f ( x) liên tục trên , có đồ thị như hình vẽ. Có tất cả 8x
bao nhiêu giá trị nguyên của tham số a để hàm số y = f + a −1
có giá trị lớn nhất không 2 x +1 vượt quá 20? A. 41. B. 31. C. 35. D. 29.
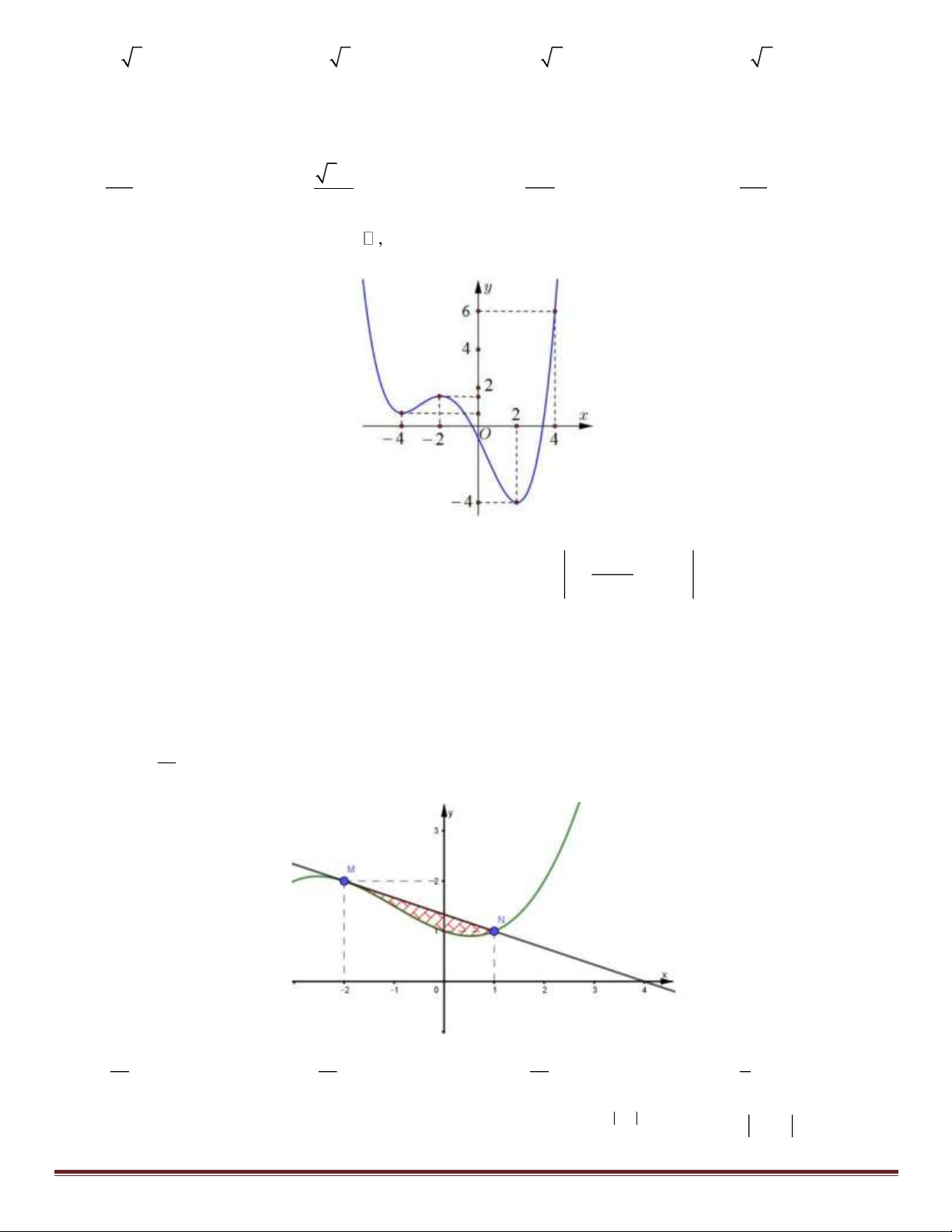
Câu 47: Cho f ( x) là hàm đa thức bậc 3 có đồ thị như hình vẽ. Tiếp tuyến của đồ thị hàm số tại điểm M có hoành độ bằng 2
− cắt đồ thị tại điểm thứ hai N (1; )
1 cắt Ox tại điểm có hoành độ bằng 4. Biết diện tích phần 1
gạch chéo là 9 . Tích phân f
(x)dx bằng 16 1 − 31 13 19 7 A. B. C. D. 18 6 9 3 2 − + − −
Câu 48: Tổng tất cả các giá trị của tham số m để phương trình x 2x 1 2 3 x m = log
2 x − m + 2 có đúng 2 x −2x+3 ( ) ba nghiệm phân biệt là Trang 7 A. 3 B. 0 C. 2 D. 1
Câu 49: Cho các số phức z = 1+ 3i, z = 5
− − 3i . Tìm điểm M ( ;
x y) biểu diễn số phức z , biết rằng trong mặt 1 2 3
phẳng phức điểm M nằm trên đường thẳng x − 2y +1= 0 và mô đun số phức w = 3z − z − 2z đạt giá trị nhỏ 3 2 1 nhất. 3 1 3 1 3 1 3 1 A. M ; B. M − ; − C. M ; − D. M − ; 5 5 5 5 5 5 5 5
Câu 50: Trong không gian Oxyz, cho ba điểm A(2; 2 − ;4), B( 3 − ;3;− ) 1 ,C ( 1 − ; 1 − ;− ) 1 và mặt phẳng
(P):2x− y +2z +8 = 0. Xét điểm M thay đổi thuộc (P), tìm giá trị nhỏ nhất của biểu thức 2 2 2
T = 2MA + MB − MC . A. 102 B. 35 C. 105 D. 30
---------------- HẾT --------------- BẢNG ĐÁP ÁN 1-B 2-C 3-B 4-D 5-D 6-D 7-A 8-A 9-D 10-A 11-C 12-C 13-C 14-C 15-A 16-A 17-A 18-A 19-D 20-C 21-C 22-B 23-A 24-C 25-B 26-D 27-D 28-C 29-A 30-C 31-D 32-A 33-B 34-A 35-C 36-A 37-D 38-A 39-B 40-D 41-D 42-A 43-A 44-B 45-A 46-B 47-B 48-A 49-D 50-A
HƯỚNG DẪN GIẢI CHI TIẾT Câu 1: Chọn B.
Số tập con thỏa mãn đề bài chính là số cách chọn 2 phần tử lấy trong tập hợp M có 12 phần tử. Số tập con gồm
2 phần tử của tập hợp M là 2 C . 12 Câu 2: Chọn C.
Ta có u = u +13d = u +10d = 18 d = 3. 14 1 4
Vậy công sai của cấp số cộng là d = 3. Câu 3: Chọn B.
Sử dụng tính chất của hai mặt phẳng vuông góc. Câu 4: Chọn D. Trang 8
Hàm số đạt cực đại tại điểm x mà f '( x) đổi dấu từ dương sang âm.
Từ bảng biến thiên ta thấy hàm số đạt cực đại tại x = 1. Câu 5: Chọn D. 1 2 + 2x +1 Ta có lim = lim
x = 2. Suy ra đồ thị hàm số có tiệm cận ngang là y = 2. x→ x −1 x→ 1 1− x Câu 6: Chọn D.
Đường cong có dạng của đồ thị hàm số bậc 3 với hệ số a 0 nên chỉ có hàm số 3
y = −x + 3x +1 thỏa yêu cầu bài toán. Câu 7: Chọn A. 1
Số nghiệm của phương trình f ( x) 1
= − bằng số nghiệm của đồ thị hàm số y = f (x) và đường thẳng y = − . 2 2 1
Dựa vào đồ thị ta thấy: đồ thị hàm số y = f ( x) và đường thẳng y = − cắt nhau tại 2 điểm. 2
Nên phương trình f (x) 1 = − có 2 nghiệm. 2 Câu 8: Chọn A.
Ta có: z z = 5i 2020 + i = 5
− +10100i Phần thực của số phức z z là 5. − 1 2 ( ) 1 2 Câu 9: Chọn D. 1 1 x+ 1 x+ 1 1 x+ 1 Ta có 3 1 3 1 e dx = e d (3x + ) 3 1 1 = e = ( 4 e − e). 3 3 0 3 0 0 Câu 10: Chọn A.
Ta có 1− 2.1+ 6 − 5 = 0 nên M (1;1;6) thuộc mặt phẳng ( P). Câu 11: Chọn C. Trang 9
Ta có ( ACGE) (BDHF ) = IJ nên khẳng định C sai. Câu 12: Chọn C. 1 1 Ta có 2 3 V = . B h =
6a .2a = 4a . 3 3 Câu 13: Chọn C. x 1 e + Ta có x e dx = + C sai vì x x
e dx = e + C. x +1 Câu 14: Chọn C.
Ta có: a + b + c = (2;6;2).
Vậy a + b + c = 2 11. Câu 15: Chọn A. = 2 2 x 0 − − Ta có x 2x x 2 x 0 2 3 =1 3
= 3 x − 2x = 0 . x = 2 Câu 16: Chọn A.
Ta thấy đường thẳng d có một vectơ chỉ phương có tọa độ u = 1; 2 − ;3 . 2 ( ) Câu 17: Chọn A. Số phức z = 2
− + 4i được biểu diễn bởi điểm C ( 2 − ;4). Câu 18: Chọn A. 3 1 3 Ta có I = f
(x)dx = f
(x)dx+ f
(x)dx = 2+6 =8. 0 0 1 Câu 19: Chọn D. 1 1
Khối nón có bán kính bằng 3 nên có thể tích là 2 3
V = r h = . .3 .4 = 12 . 3 3 Câu 20: Chọn C.
Thể tích của khối hộp đã cho bằng 2.4.6 = 48. Câu 21: Chọn C.
Ta có z + z = 1− 2i + 2 + i = 3 − . i 1 2
Thầy cô có nhu cầu mua trọn bộ đề thi thử theo minh họa mới năm 2021 môn Toán vui lòng liên hệ số điên thoại 096.458.1881 Câu 22: Chọn B. Trang 10
Từ phương trình mặt cầu suy ra tâm của mặt cầu là I (2; 1 − ;3). Câu 23: Chọn A.
Từ bảng biến thiên ta thấy hàm số đã cho nghịch biến trên khoảng (0 ) ;1 . Câu 24: Chọn C. Điều kiện: x 9 − Ta có: log ( x + 9) 5
= 5 x + 9 = 2 x = 23. 2 Câu 25: Chọn B.
Theo tính chất của lũy thừa thì đẳng thức x + y = ( x + y) sai. Câu 26: Chọn D.
Theo công thức tính diện tích xung quanh hình trụ S
= 2 rh = 2.2.5 = 20. xq Câu 27: Chọn D.
Đường thẳng đi qua A và vuông góc với mặt phẳng (BCD) nhận vectơ pháp tuyến của (BCD) là vectơ chỉ phương. Ta có BC = (2;0;− ) 1 , BD = (0; 1 − ;2).
u = n = BC, BD = ( 1 − ; 4 − ; 2 − ). d
Khi đó ta loại phương án A và B 1 = 2 + t t = 1 −
Thay điểm A(1;02) vào phương trình ở phương án D ta có 0 = 4 + 4t t = 1 − . 2 = 4 + 2t t = 1 −
Suy ra đường thẳng có phương trình tham số ở phương án C đi qua điểm A nên D là phương án đúng. Câu 28: Chọn C. 3 1 + 2− 3 3 1 + +2− 3 3 a .a a a Ta có 5 P = = = = ( − ) + ( − )( + ) a . 2 2 2 2 2 2 2 − 2 2 a a a Câu 29: Chọn A. 1 1 1
Ta có ( f (x) − 2g (x))dx = f
(x)dx−2 g
(x)dx = 2−2.5 = 8 − . 0 0 0 Câu 30: Chọn C. x Ta có: 2 3 F (x) = f (x)dx = 3 x + (1− 2 )
m x + 2m dx = x + (1− 2 )
m . + 2mx + C 2 Trang 11 C = 3 C = 3 F(0) = 3 Ta có: = 1 = 1 − 5 F(1) = 3 −
1+ (1− 2m). + 2m + C = 3 − m = 2 2 Câu 31: Chọn D.
Điều kiện: x 0 . BPT 2
= log x log x − log 4 + 4 = log x + 2 2 2 2 2 x 4 log x 2 2 (log x 2)(log x 1) 0 = − + = = 1 . 2 2 log x 1 − x 2 2 1 Vậy x 0; 4;+ ) . 2 Câu 32: Chọn A.
Xem ba chữ T riêng biệt ta có: n() = 6!.
Gọi A là biến cố “xếp ngẫu nhiên 6 thẻ đó thành dãy TNTHPT”, suy ra n( A) = 3!
(số hoán vị của T – T – T và N, H, P cố định).
Vậy xác suất của biến cố A P ( A) 3! 1 : = = . 6! 120 Câu 33: Chọn B. x x Ta có (x − x) 2 cos 2 sin 2
dx = xdx − sin 2xdx = + + . C 2 2 Câu 34: Chọn A. + i Ta có ( + i) 1 3 1
z −1− 3i = 0 z =
z = 2 + i z = 2 − .i 1+ i
Do đó w =1− iz + z =1− i (2 −i) + 2 + i = 2 − .i
Vậy phần ảo của số phức w = 1− iz + z là 1. − Câu 35: Chọn C. 2 2 2
Ta có R = IA = (1− ) 1 + (2 − ) 1 + (3 − ) 1 = 5.
Vậy phương trình mặt cầu tâm I và đi qua điểm A có phương trình là
(x − x )2 +( y − y )2 +(z − z )2 = R (x − )2 +( y − )2 + (z − )2 2 1 1 1 = 5. I I I Câu 36: Chọn A. Trang 12 2 2 x −3x−7 1 − − − x− ( 2 2 x 3x 7 2 21 ) Ta có 2 x−21 3 3 3 3 −( 2 x − x − ) 2 2 3 7 2x − 21 2
− x + 3x + 7 2x − 21 7 2 2
− x + x + 28 0 − x 4. 2
Do x nên x 3 − ; 2 − ; 1 − ;0;1;2; 3 .
Vậy bất phương trình đã cho có 7 nghiệm nguyên. Câu 37: Chọn D. Tập xác định D = . −12x y ' = ( 3x + ) . 2 2 1 2
Ta có y ' 0 x 0 nên hàm số y =
nghịch biến trên khoảng (0;+). 2 3x +1 Câu 38: Chọn A.
Xét hàm số g ( x) = f ( x) + ( − x)2 2 1 trên 4 − ; 3 .
Ta có: g '( x) = 2. f '( x) − 2(1− x).
g '( x) = 0 f '( x) =1− .
x Trên đồ thị hàm số f '( x) ta vẽ thêm đường thẳng y =1− . x x = 4 −
Từ đồ thị ta thấy f '( x) = 1− x x = 1 − . x = 3
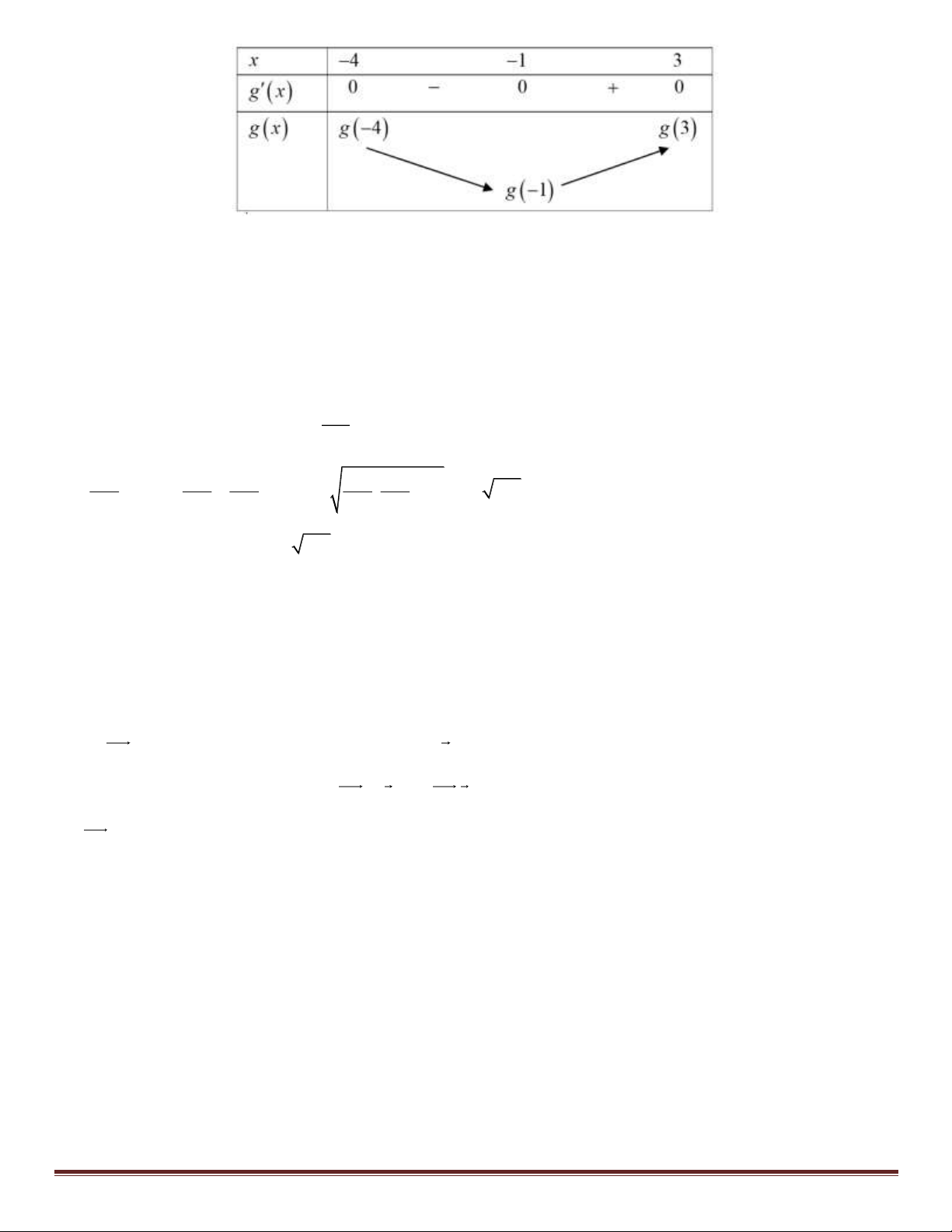
Bảng biến thiên của hàm số g ( x) như sau: Trang 13
Vậy min g ( x) = g (− ) 1 x = 1 − . 4 − ;3 Câu 39: Chọn B.
Gọi chiều rộng, chiều dài của đáy lần lượt là x và 2 , x chiều cao là . y
Diện tích các mặt bên và mặt đáy là 2
S = 6xy + 2x 100 Thể tích là 2
V = 2x y = 200 xy = . x 600 300 300 300 300 2 2 2 3 3 S = + 2x = + + 2x 3 . .2x = 30 180 x x x x x
Vậy chi phí thấp nhất là 3
T = 30 180.3000000 = 51 triệu. Câu 40: Chọn D. x =1+ t
Phương trình tham số của đường thẳng d : y = 2 + t z = 3+t
Gọi là đường thẳng cần tìm. Theo đề bài d cắt nên gọi I = d = I d suy ra I(1+ t;2 + t;3+ t) .
Ta có MI = (t;t;t +1) ; mặt phẳng (P) có VTPT là n = (1; −1;1) .
song song với mặt phẳng (P) nên MI ⊥ n = MI.n = 0 = 1.t + ( 1
− ).t +1.(1+ t) = 0 = t = −1 = MI = ( 1 − ; 1
− ;0) là 1 VTCP của đường thẳng và đi qua điểm M(1;2;2). x = 1− t '
Vật PTTS của đường thẳng cần tìm là y = 2 − t '. z = 2 Câu 41: Chọn D. Ta có: 2 2 2 2 2 2
| z + 2 | = (a + 2) + b ;| z − 2 | = (a − 2) + b 2 2 2 2 2 = |
z + 2 | + | z − 2 | = 2(a + b ) + 8 = 2 | z | 8 + =10 Ta có: 2 2 2 2 2 2 A = (| z + 2 | 2
+ | z − 2 |) (1 + 2 )(| z + 2 | + | z − 2 | ) = 50 . Trang 14
Vì A 0 nên từ đó suy ra A 50 = 5 2 .
Vậy giá trị lớn nhất của A là 5 2 . Câu 42: Chọn A. 2
f '(x)(1+ f (x)) Ta có: 2 2 2 2.
f '(x)(1+ f (x)) = [( f (x)) (x −1)] = = (x −1) 4 f (x) 2 +
Lấy nguyên hàm 2 vế ta được f '(x)(1 f (x)) 2
dx = (x −1) dx 4 f (x) 2
(1+ 2 f (x) + f (x)) f '(x) 2 =
dx = (x −1) dx 4 f (x) 3 1 1 1 (x −1) = + 2 +
d ( f (x)) = + C 4 3 2 f (x) f (x) f (x) 3 3 1 1 1 (x −1) = − − − = + C 3 2 3 f (x) f (x) f (x) 3 2 3
1+ 3 f (x) + 3 f (x) (x −1) = − = + C 3 3 f (x) 3 1− 3 + 3 1 Mà f (1) = 1 − = − = C = C = . 3 − 3 2 3
1+ 3 f (x) + 3 f (x) (x −1) 1 = − = + 3 3 f (x) 3 3 2 3
1+ 3 f (x) + 3 f (x) 1 (x −1) = + = − 3 3 f (x) 3 3 3 (1+ f (x)) 3 = = −(x −1) 3 f (x) 3 1 3 = 1+ = (1− x) f (x) 1 − = f (x) = . x 3 3 1 − 3 Vậy f (x)dx =
dx = − ln | x | = −ln 3 . Suy ra a = 1
− ;b = 0 hay a + b = 1 − . x 1 1 1 Câu 43: Chọn A , x y N*: , x y 2020 , x y N*: , x y 2020 Điều kiện 2x +1 2 y = . 0, 0
x 3, y 0 x − 3 y + 2 x + 4 y − 2
BPT cho có dạng (x − 3)( y − 2) log
+1 + (x + 4)(y + 2)log +1 0(*). 2 3 x − 2 y + 2 Trang 15 x + 4 2
Xét y =1 thì (*) thành ( − x −3)log +1 + 3(x + 4)log 0
, rõ ràng BPT này nghiệm đúng với mọi 2 3 x −3 3 x + 4 2 x 3 vì ( − x −3) 0;log
+1 log (0 +1) = 0,3(x + 4) 0,log 0. 2 2 3 x −3 3
Như vậy trường hợp này cho ta đúng 2017 bộ ( ; x ) y = ( ;
x 1) với 4 x 2020, x .
Xét y = 2 thì (*) thành 4(x + 4) log 1 0, BPT này cũng luôn đúng với mọi x mà 4 x 2020, x . 3
Trường hợp này cho ta 2017 cặp ( ; x y) nữa.
Với y 2, x 3 thì VT(*) > 0 nên (*) không xảy ra
Vậy có đúng 4034 bộ số ( ;
x y) thỏa mãn yêu cầu bài toán. Câu 44: Chọn B.
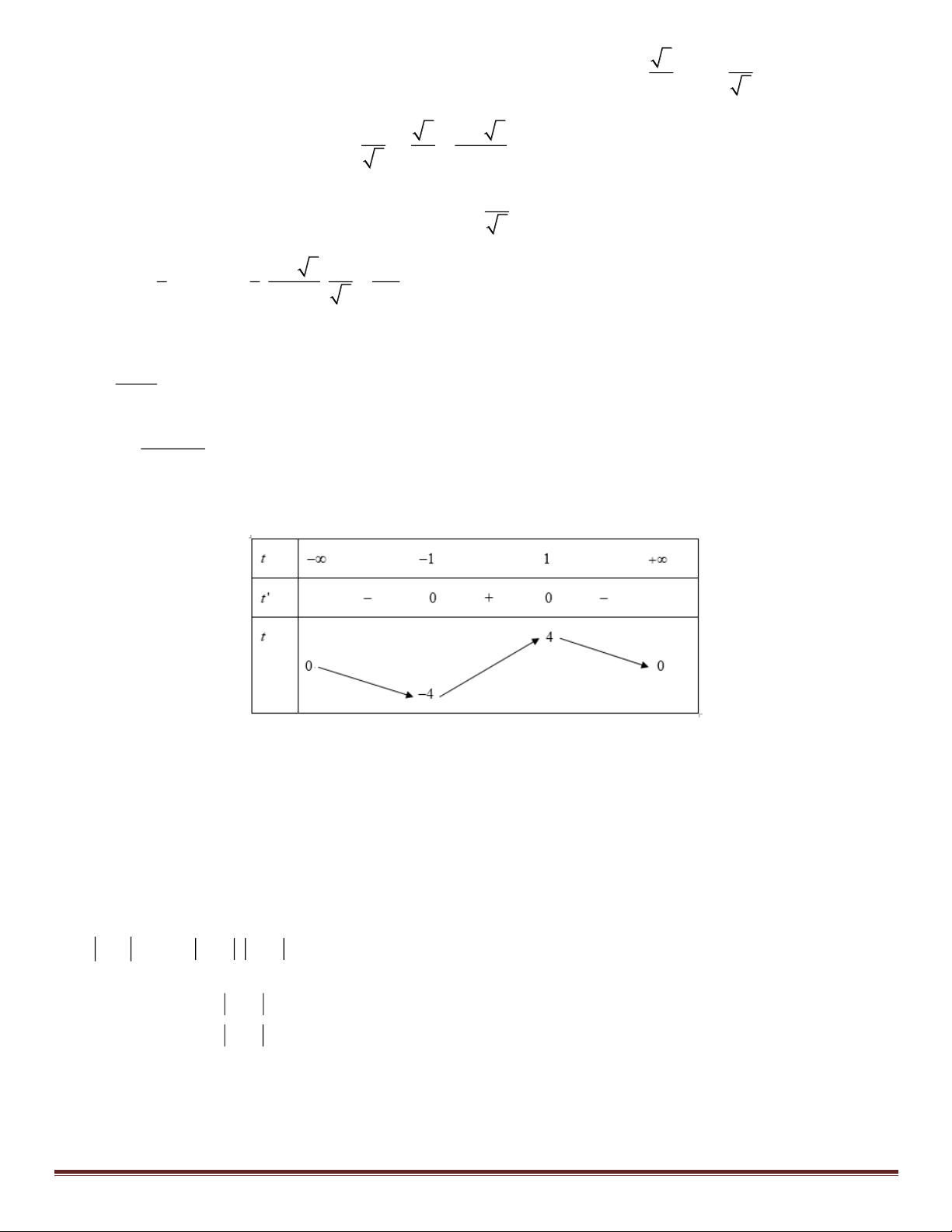
ĐTHS có 3 điểm cực trị 2 = ab = 2
− m 0 = m 0. 4 ( A 0;1) AB = ( ; m −m ) x = 0 Ta có: 3 2 4 4
y ' = 4x − 4m x = 0 = = B( ;1
m − m ) = AC = (− ; m −m ) . x = m 4 C(− ;1 m − m ) BC = ( 2 − ; m 0) 2 2 2 8
AB = AC = m + m 2 8 2 6 6 =
= m + m = 4m = m = 3 = m = 3. 2 2 BC = 4m Câu 45: Chọn A.
Gọi I là trung điểm của BC suy ra góc giữa mp (SBC) và mp( ABC) là 0 SIA = 30 .
H là hình chiếu vuông góc của A trên SI suy ra d ( ,
A (SBC)) = AH = . a AH
Xét tam giác AHI vuông tại H suy ra AI = = 2 . a 0 sin 30 Trang 16 3 4a
Giả sử tam giác đều ABC có cạnh bằng x, mà AI là đường cao suy ra 2a = x x = . 2 3 2 2 4a 3 4a 3
Diện tích tam giác đều ABC là S = . = . ABC 3 4 3 2a
Xét tam giác SAI vuông tại A suy ra 0
SA = AI. tan 30 = . 3 2 3 1 1 4a 3 2a 8a Vậy V = .S .SA = . . = . S . ABC 3 ABC 3 3 3 9 Câu 46: Chọn B. Đặ 8x t t = . 2 x +1 2 8 − x + 8 Ta có: t ' = ( = = x + ) ;t ' 0 x 1. 2 2 1 Bảng biến thiên: t 4 − ; 4 .
Xét hàm số: h(t) = f (t) + a −1,t 4 − ;
4 , ta có: h '(t ) = f '(t ). t = 4 − 4 − ;4
h '(t ) = 0 f '(t ) = 0 t = 2 − 4 − ;4. t = 2 4 − ;4
max h (t ) = Max a + 5 ; a − 5. 4 − ;4 a + 5 20 2 − 0 a + 5 20 2 − 5 a 15 Yêu cầu bài toán 1 − 5 a 15 . a − 5 20 2
− 0 a − 5 20 1 − 5 a 25
Vậy có tất cả 31 giá trị nguyên của tham số a thỏa mãn yêu cầu bài toán. Câu 47: Chọn B. Trang 17 1 − 4
Dựa vào giả thiết đường thẳng đi qua hai điểm M ( 2
− ;2) và P(4;0). Suy ra d : x + 3y − 4 = 0 y = x + . 3 3
Từ giả thiết ta có hàm số f ( x) 3 2
= ax + bx + cx + d f (x) 2 ' = 3ax + 2bx + .
c Chú ý đồ thị hàm số tiếp xúc
đường thẳng d tại x = 2. − 1 1 = 8
− a + 4b − 2c a = 12
0 = a + b + c 1 1 1 1 3 2 1 b = y = x + x − x +1.
12a − 4b + c = − 4 12 4 3 3 1 =1 c d = − 3 1 13 Từ đó f (x)dx = . 6 1 − Câu 48: Chọn A. ln 2 x − m + 2
Phương trình tương đương 2x−2x+3−(2 x−m +2) ( ) 3 = ln ( . 2 x − 2x + 3) 2 x −2x+3 ( 2 − + 3 .ln x − 2x + ) 2 x m 2 3 = 3
.ln (2 x − m + 2)( ) * .
Xét hàm đặc trưng ( ) = 3t f t
.ln t,t 2 là hàm số đồng biến nên từ phương trình ( ) * suy ra 2
x − x + = x − m + g (x) 2 2 3 2 2
= x − 2x − 2 x − m +1= 0. 2
x − 4x + 2m + 2 khi x m
2x − 4 khi x m Có g ( x) = g '(x) = . 2
x − 2m +1 khi x m
2x khi x m x = x m Và g ( x) 2 khi ' = 0
x = 0 khi x m
Xét các trường hợp sau:
Trường hợp 1: m 0 ta có bảng biến thiên của g (x) như sau:
Phương trình chỉ có tối đa 2 nghiệm nên không có m thỏa mãn. Trang 18
Trường hợp 2: m 2 tương tự.
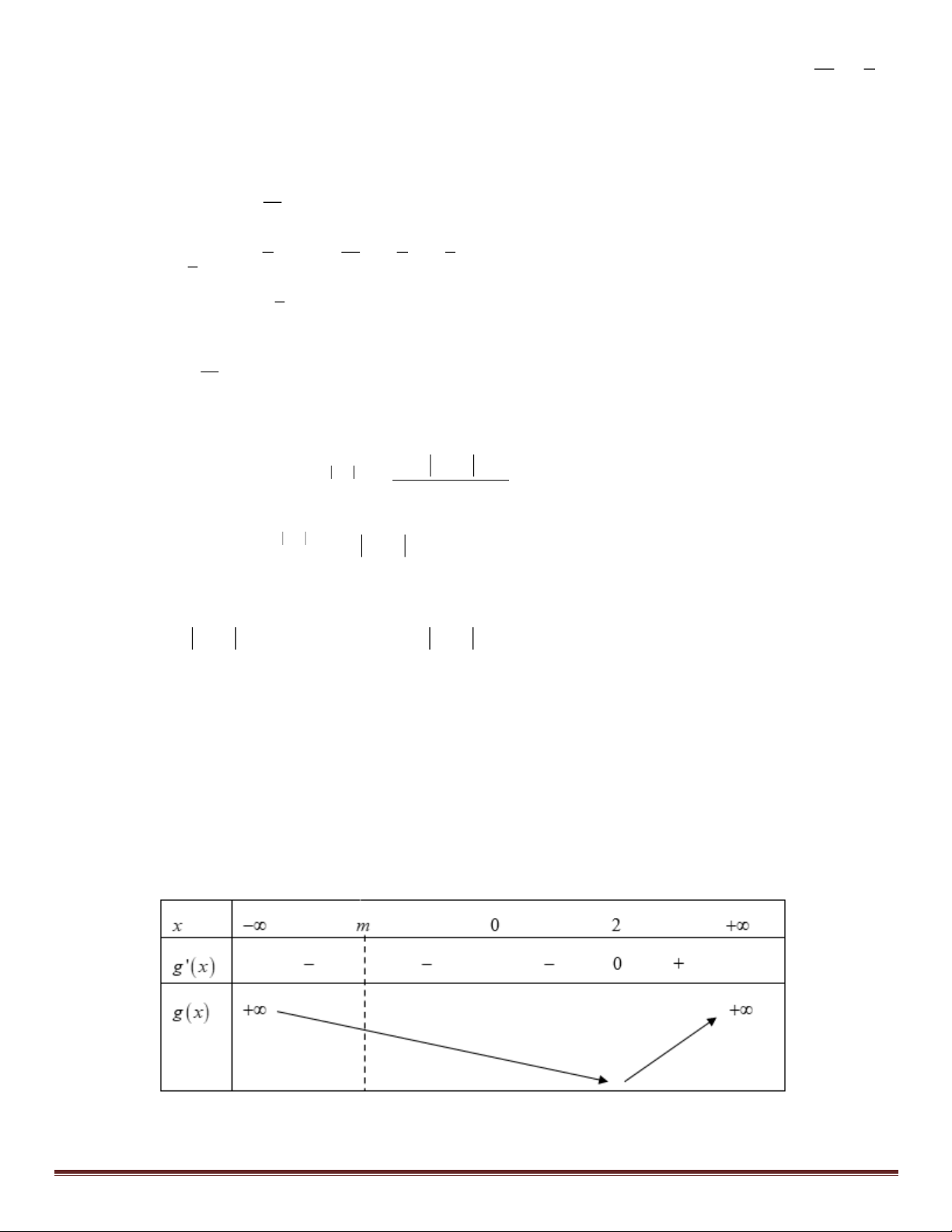
Trường hợp 3: 0 m 2, bảng biến thiên g (x) như sau: ( = m − )2 m 1 1 = 0 Phương trình có 3 nghiệ 1 m khi 2
− m +1 = 0 2m − 3 m = . 2 2
− m +1 0 = 2m − 3 3 m = 2 Câu 49: Chọn D.
Trắc nghiệm: Thay tọa độ điểm M vào vế trái phương trình đường thẳng kết quả bằng 0 thỏa ta được đáp án A. Tự luận:
Ta có w = 3z − z − 2z = 3z + 3 − 3i = 3 z +1− i → w = 3 z +1− i = 3AM với A( 1 − ;3) 3 2 1 3 ( 3 ) 3 M ( ;
x y) biểu diễn số phức z nằm trên đường thẳng d : x − 2y +1= 0 và A( 1 − ; ) 3 d. 3
Khi đó w = 3 z +1−i = 3AM đạt giá trị nhỏ nhất khi AM ngắn nhất AM ⊥ d 3
AM ⊥ d nên AM có phương trình: 2x + y +1 = 0. Khi đó 3 1
M = AM d nên M − ; . 5 5 Câu 50: Chọn A.
Gọi I là điểm thỏa mãn: 2IA + IB − IC = 0
2(OA−OI )+(OB −OI )−(OC −OI ) = 0 1 1
OI = OA+ OB − OC = (1;0;4) 2 2 I (1;0;4).
Khi đó, với mọi điểm M ( ; x ;
y z)(P), ta luôn có
T = (MI + IA)2 + (MI + IB)2 − (MI + IC )2 2 Trang 19 2
= MI + MI ( IA+ IB − IC) 2 2 2 2 2 . 2
+ 2IA + IB − IC 2 2 2 2
= 2MI + 2IA + IB − IC . Ta tính được 2 2 2
2IA + IB − IC = 30.
Do đó, T đạt GTNN MI đạt GTNN MI ⊥ (P). 2.1− 0 + 2.4 + 8
Lúc này, IM = d (I,(P)) = = 6. 2 + (− )2 2 2 1 + 2 Vậy 2 T = 2.6 + 30 =102. min Trang 20