Đề Thi Thử TN 2022 Môn Toán Chuyên Lam Sơn Có Lời Giải Chi Tiết-Lần 2

Đề thi thử TN 2022 môn Toán chuyên Lam Sơn có đáp án chi tiết được soạn dưới dạng file PDF. Đề thi bao có 24 trang. Đề thi có đáp án chi tiết phía dưới giúp các bạn so sánh đối chiếu kết quả một cách chính xác. Mời các bạn cùng đón xem ở dưới.

20 10 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

24 trang 8 tháng trước

Tác giả:

Profile ha phan
Trang1
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐỀ THI CHÍNH THỨC
( Đề thi có 06 trang)
KỲ THI KSCL CÁC MÔN THI TN THPT NĂM 2022 - LẦN 2
Môn thi: Toán
Ngày thi: 03/04/2022
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Họ và tên: ............................................................................
Số báo danh: .............
Mã đề Gốc
Câu 1. Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập
2, 3, 4, 5, 6A
A.
4
5
C
. B.
4
6
C
. C.
4
5
A
. D.
4
6
A
.
Câu 2. Cho cấp số nhân
n
u
với
và
2
4u
. Công bội của cấp số nhân đã cho bằng
A.
1
2
. B.
1
2
. C.
2
. D.
2
.
Câu 3. Hàm số nào sau đây đồng biến trên
?
A.
3
3y x x
. B.
3
3y x x
. C.
1
1
x
y
x
. D.
42
31y x x
.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
3x 
. B.
1x 
. C.
1x
. D.
2x 
.
Câu 5. Hàm số
42
3y x x
có mấy điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Câu 6. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số
51
2
x
y
x
?
A.
5y
. B.
5x
. C.
2x
. D.
2x 
.
Câu 7. Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
A.
32
1y x x x
. B.
yx
. C.
1
2
x
y
x
. D.
3
logyx
.
Câu 8. Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ dưới đây.
Trang2
Số nghiệm của phương trình
1fx
là:
A.3. B.0. C.2. D.1.
Câu 9. Tập xác định của hàm số
3
5
1yx
là
A.
1; 
. B.
0;
. C.
1; 
. D.
\1
.
Câu 10. Hàm số
4
2
x
fx
có đạo hàm là
A.
4
2 .ln2
x
fx
. B.
4
4.2 .ln2
x
fx
. C.
4
2
ln2
x
fx
. D.
4
4.2
ln2
x
fx
.
Câu 11. Tập nghiệm của phương trình
log 1 log 2 3 0xx
là
A.
2
4;
3



. B.
2
.
C.
4
.
D.
.
Câu 12. Trên khoảng
;2
, họ nguyên hàm của hàm số
1
()
2
fx
x
là
A.
1
2
C
x
. B.
ln 2xC
. C.
2
1
2
C
x
. D.
1
ln 2
2
xC
.
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai?
A.
df x x f x C

. B.
cos d sinx x x C
.
C.
1
d , 1
1
x
x x C
. D.
d ln
xx
a x a a C
01a
.
Câu 14. Tích phân
1
3
0
ed
x
x
bằng
A.
3
1
e
2
. B.
e1
. C.
3
e1
3
. D.
3
e1
.
Câu 15. Xét
1
2022
2
0
22I x x dx
, nếu đặt
2
2ux
thì
I
bằng
A.
3
2022
2
u du
. B.
1
2022
0
u du
. C.
3
2022
2
2 u du
. D.
3
2022
2
1
2
u du
.
Câu 16. Cho số phức
32zi
. Tìm phần ảo của số phức liên hợp của
z
.
A.
2
. B.
2i
. C.
2
. D.
2i
.
Câu 17. Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Câu 18. Xét hai số phức
1
z
,
2
z
tùy ý. Phát biểu nào sau đây sai?
A.
1 2 1 2
.z z z z
. B.
1 2 1 2
.z z z z
. C.
1 2 1 2
z z z z
. D.
1 2 1 2
z z z z
.
Câu 19. Một khối lăng trụ có thể tích bằng
V
, diện tích mặt đáy bằng
S
. Chiều cao của khối lăng trụ
đó bằng
A.
S
V
. B.
3V
S
. C.
V
S
. D.
3
S
V
.
Câu 20. Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ bên dưới).
Trang3
Thể tích của khối chóp đã cho bằng:
A.
. B.
. C.
3
3a
. D.
3
3
12
a
.
Câu 21. Cho hình nón có bán kính đáy
3R
và độ dài đường sinh
4l
. Tính diện tích xung quanh
xq
S
của hình nón đã cho.
A.
12
xq
S
. B.
43
xq
S
. C.
39
xq
S
. D.
83
xq
S
.
Câu 22. Tính thể tích của khối trụ biết bán kính đáy của khối trụ đó bằng
a
và chiều cao bằng
2a
A.
3
2 a
. B.
3
a
. C.
3
4 a
. D.
2
2 a
.
Câu 23. Trong không gian với hệ trục tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2;3A
trên mặt
phẳng
Oyz
là
A.
0;2;3M
. B.
1;0;3N
. C.
1;0;0P
. D.
0;2;0Q
.
Câu 24. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
(1; 2 ; 3)A
và mặt phẳng
( ):3 4 7 2 0P x y z
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
()P
có phương
trình là
A.
3
4 2 ( ).
73
xt
y t t
zt


B.
13
2 4 ( ).
37
xt
y t t
zt


C.
13
2 4 ( ).
37
xt
y t t
zt


D.
14
2 3 ( ).
37
xt
y t t
zt


Câu 25. Trong không gian với hệ trục tọa độ
Oxyz
, mặt cầu tâm
1;0;0I
và bán kính bằng
2
có
phương trình là
A.
2
22
12x y z
. B.
2
22
12x y z
.
C.
2
22
14x y z
. D.
2
22
14x y z
.
Câu 26. Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống
nhau, một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp
theo hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là
A.
1
7
. B.
. C.
2
7!
. D.
1
7!
.
Câu 27. Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
3AB a
,
3BC a
;
SA
vuông góc
với mặt phẳng đáy và
2SA a
. Góc giữa đường thẳng
SC
và mặt phẳng đáy
ABC
bằng
A.
ο
60
. B.
ο
45
. C.
ο
30
. D.
ο
90
.
Câu 28. Cho hàm số bậc bốn
y f x
. Hàm số
y f x
có đồ thị như hình vẽ như sau
Trang4
Hàm số
y f x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1;4
. B.
1;1
. C.
0;3
. D.
;0
.
Câu 29. Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: nếu trên mỗi
mét vuông mặt hồ thả
x
con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là
2
108 x
(gam). Hỏi nên thả bao nhiêu con tôm giống trên mỗi mét vuông mặt hồ tự nhiên đó để
cuối vụ thu hoạch được nhiều tôm nhất.
A.6. B.7. C.8. D.9.
Câu 30. Xét tất cả các số dương
a
và
b
thỏa mãn
3 3 9
log log loga b ab
. Tính giá trị của
ab
.
A.
1ab
. B.
2ab
. C.
1
2
ab
. D.
0ab
.
Câu 31. Tích tất cả các nghiệm của phương trình
2
2 5 4
24
xx
bằng
A.
1
. B.
2
. C.
2
. D.
1
.
Câu 32. Số nghiệm nguyên của bất phương trình
2
3x
52
1
5
5
x



là
A.
3
. B.
1
. C.
2
. D.
4
.
Câu 33. Cho hàm số
fx
liên tục trên đoạn
0;1
,có đạo hàm
fx
thỏa mãn
1
0
2 1 d 10x f x x

và
0 3 1ff
. Tính
1
0
dI f x x
.
A.
5I 
. B.
2I 
. C.
2I
. D.
5I
.
Câu 34. Tìm số phức
z
thỏa mãn
2 9 2z z i
.
A.
32zi
. B.
3zi
. C.
32zi
. D.
23zi
.
Câu 35. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
21
:
3 1 2
x y z
. Gọi
M
là
giao điểm của
với mặt phẳng
: 2 3 2 0P x y z
. Tọa độ điểm
M
là
A.
2;0; 1M
. B.
5; 1; 3M 
. C.
1;0;1M
. D.
1;1;1M
.
Câu 36. Trong không gian với hệ trục tọa độ
Oxyz
,
P
là mặt phẳng đi qua điểm
1;2;3M
và cắt các
tia
,,Ox Oy Oz
lần lượt tại
,,A B C
(khác gốc tọa độ
O
) sao cho
M
là trực tâm tam giác
ABC
.
Biết mặt phẳng
P
có phương trình
14 0ax by cz
. Tính tổng
T a b c
.
A.8. B.14. C.6. D.11.
Câu 37. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
7; 1;2A
và mặt phẳng
: 2 2 6 0P x y z
. Mă
t câu
S
tâm
A
và tiếp xc với mặt phẳng
P
có phương trình
là
A.
2 2 2
49
7 1 2
9
x y z
. B.
2 2 2
7
7 1 2
3
x y z
.
C.
2 2 2
49
7 1 2
9
x y z
. D.
2 2 2
7
7 1 2
3
x y z
.
Câu 38. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Cạnh
'3BA a
.
Khoảng cách giữa hai đường thẳng
'AB
và
'BC
là:
Trang5
A.
2a
. B.
3
a
.
C.
2
3
a
. D.
2
3
a
.
Câu 39. Gọi là tập hợp tất cả các giá trị thực của tham số để đồ thị của hàm số
có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ
tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của .
A.
2
. B.
1
5
. C.
1
5
. D.
2
.
Câu 40. Gọi
S
là tập nghiệm của bất phương trình
22
log 2 log 2 3
aa
x x x x
. Biết
;S m n
và
7
3
thuộc
S
, tính
mn
.
A.
13
3
mn
. B.
7
2
mn
. C.
11
3
mn
. D.
9
2
mn
.
Câu 41. Cho hàm số
y f x
liên tục trên đoạn
0;
2



thỏa mãn:
2cos . 1 4sin sin2 . 3 2cos2 sin4 4sin2 4cosx f x x f x x x x
,
0;
2
x




.
Khi đó
5
1
I f x dx
bằng
A.2. B.4. C.
8
. D.
16
.
Câu 42. Có bao nhiêu số phức
z
thỏa mãn
1 2 2zi
và
4 4 10zz
?
A.
1
. B.
0
. C.
2
. D.
4
.
Câu 43. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
, tam giác
SAB
cân tại
S
và thuộc
mặt phẳng vuông góc với mặt phẳng
ABC
, góc giữa hai mặt phẳng
SCA
và
SCB
bằng
0
60
. Gọi
H
là trung điểm của đoạn
AB
. Trong các mệnh đề sau, mệnh đề nào đng:
A.Thể tích khối chóp
.S ABC
bằng
3
2
16
a
. B.Thể tích khối chóp
.B SHC
bằng
3
2
16
a
.
C.Thể tích khối chóp
.S AHC
bằng
3
2
64
a
. D.Không tồn tại hình chóp đã cho.
Câu 44. Một cái bình thủy tinh có phần không gian bên trong là một hình nón có đỉnh hướng xuống
dưới theo chiều thẳng đứng. Rót nước vào bình cho đến khi phần không gian trống trong bình
có chiều cao 2 cm. Sau đó đậy kín miệng bình bởi một cái nắp phẳng và lật ngược bình để đỉnh
hướng lên trên theo chiều thẳng đứng, khi đó mực nước cao cách đỉnh của nón 8 cm (hình vẽ
minh họa bên dưới).
Biết chiều cao của nón là
h a b
cm. Tính
T a b
.
A.
22
. B.
58
. C.
86
. D.
72
.
S
m
C
4 2 2 4
25y x m x m
O
S
8 cm
2 cm
Trang6
Câu 45. Trong không gian với hệ trục tọa độ
Oxyz
cho điểm
1;0;0I
, điểm
7 4 4
;;
999
M



và đường
thẳng
2
:
1
x
d y t
zt

.
,,N a b c
là điểm thuộc đường thẳng
d
sao cho diện tích tam giác
IMN
nhỏ nhất. Khi đó
abc
có giá trị bằng:
A.
2
. B.
2
. C.
5
2
. D.
5
2
.
Câu 46. Cho hàm số
4 3 2
2 1 2 2022f x x x m x x m
, với
m
là tham số. Có bao nhiêu giá
trị nguyên của
m
thuộc đoạn
2021;2022
để hàm số
2021 2022y f x
có số điểm
cực trị nhiều nhất?
A.2021. B.2022. C.4040. D.2023
Câu 47. Có bao nhiêu số nguyên dương
m
để phương trình
2
1 .ln( 1) 2 1
x x x
m e mx e e
có
2
nghiệm phân biệt không lớn hơn 5.
A.26. B.27. C.29. D.28.
Câu 48. Cho hàm số
fx
với đồ thị là Parabol đỉnh
I
có tung độ bằng
7
12
và hàm số bậc ba
gx
.
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thoả mãn
1 2 3
18 55x x x 
(hình vẽ).
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
A.5,7. B.5,9. C.6,1. D.6,3.
Câu 49. Cho
,,M N P
lần lượt là các điểm biểu diễn số phức
1
z
,
2
z
,
3
z
thỏa mãn điều kiện
11
5 9 3 5z i z
,
22
23z z i
,
33
1 3 4zz
. Khi
,,M N P
không thẳng hàng,
giá trị nhỏ nhất của nửa chu vi
p
của tam giác
là
A.
10 5
9
. B.
65
5
. C.
9 10
10
. D.
5 11
13
.
Câu 50. Trong không gian với hệ trục tọa độ
Oxyz
, cho
3
đường thẳng
1
d
,
2
d
,
3
d
có phương
trình
1
11
1
12
:1
12
xt
d y t
zt



,
2
22
2
3
: 1 2
22
xt
d y t
zt


,
3
33
3
42
: 4 2
1
xt
d y t
zt



.
;S I R
là mặt cầu tâm
I
bán
kính
R
tiếp xúc với
3
đường thẳng đó. Giá trị nhỏ nhất của
R
gần số nào nhất trong các số
sau:
A.2,1. B.2,2. C.2,3. D.2,4.
Trang7
SỞ GD & ĐT THANH HÓA
TRƯỜNG THPT CHUYÊN LAM SƠN
ĐÁP ÁN ĐỀ GỐC
KỲ THI KSCL CÁC MÔN THI TN THPT NĂM 2022 - LẦN 2
Môn thi:Toán
Ngày thi: 03/04/2022
BẢNG ĐÁP ÁN
1.C
2.A
3.B
4.D
5.C
6.D
7.C
8.A
9.A
10.A
11.D
12.B
13.D
14.C
15.A
16.C
17.D
18.D
19.C
20.D
21.B
22.A
23.A
24.B
25.C
26.C
27.C
28.A
29.A
30.A
31.A
32.C
33.A
34.C
35.D
36.C
37.C
38.C
39.C
40.D
41.B
42.C
43.C
44.C
45.B
46.A
47.D
48.A
49.B
50.A
ĐÁP ÁN CHI TIẾT
Câu 1. Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập
2, 3, 4, 5, 6A
A.
4
5
C
. B.
4
6
C
. C.
4
5
A
. D.
4
6
A
.
Lời giải
Số các số tự nhiên có 4 chữ số khác nhau được lập từ
A
là
4
5
A
.
Câu 2. Cho cấp số nhân
n
u
với
và
2
4u
. Công bội của cấp số nhân đã cho bằng
A.
1
2
. B.
1
2
. C.
2
. D.
2
.
Lời giải
Ta có
2
21
1
1
.
2
u
u u q q
u
.
Câu 3. Hàm số nào sau đây đồng biến trên
?
A.
3
3y x x
. B.
3
3y x x
. C.
1
1
x
y
x
. D.
42
31y x x
.
Lời giải
Nhận xét
3
3y x x
có
2
3 3 0,y x x
.
Do đó hàm số
3
3y x x
đồng biến trên
.
Câu 4. Cho hàm số
y f x
có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm
A.
3x 
. B.
1x 
. C.
1x
. D.
2x 
.
Lời giải
Qua bảng biến thiên ta có hàm số đạt cực đại tại điểm
2x 
.
Câu 5. Hàm số
42
3y x x
có mấy điểm cực trị?
A.
1
. B.
2
. C.
3
. D.
0
.
Lời giải
Trang8
Hàm số
42
3y x x
có
1. 1 1 0ab
, suy ra hàm số
42
3y x x
có
3
điểm cực
trị.
Câu 6. Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số
51
2
x
y
x
?
A.
5y
. B.
5x
. C.
2x
. D.
2x 
.
Lời giải
Ta có:
2
52
lim
2
x
x
x


và
2
52
lim
2
x
x
x


nên đồ thi có TCĐ:
2x 
.
Câu 7. Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây?
A.
32
1y x x x
. B.
yx
. C.
1
2
x
y
x
. D.
3
logyx
.
Lời giải
Dễ nhận thấy dạng đồ thị cho trong bài là của hàm số dạng
ax b
y
cx d
.
Câu 8. Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ dưới đây. Số nghiệm của phương trình
1fx
là:
A.3. B.0. C.2. D.1.
Lời giải
Kẻ đường thẳng
1y
ta thấy đường thẳng
1y
cắt đồ thị tại 3 điểm phân biệt. Như vậy số nghiệm của
phương trình
1fx
là 3.
Câu 9. Tập xác định của hàm số
3
5
1yx
là
A.
1; 
. B.
0;
. C.
1; 
. D.
\1
.
Lời giải
Điều kiện xác định:
1 0 1xx
.
Vậy tập xác định của hàm số là:
1;D 
.
Câu 10. Hàm số
4
2
x
fx
có đạo hàm là
Trang9
A.
4
2 .ln2
x
fx
. B.
4
4.2 .ln2
x
fx
. C.
4
2
ln2
x
fx
. D.
4
4.2
ln2
x
fx
.
Lời giải
Áp dụng công thức
.ln .
uu
a a au
.
Ta có
4 4 4
2 2 .ln2. 4 2 .ln2
x x x
f x x
.
Câu 11. Tập nghiệm của phương trình
log 1 log 2 3 0xx
là
A.
2
4;
3



. B.
2
.
C.
4
.
D.
.
Lời giải
Ta có phương trình đã cho
1 2x 3
1
x
x
4
1
x
x

Phương trình trên vô nghiệm.
Câu 12. Trên khoảng
;2
, họ nguyên hàm của hàm số
1
()
2
fx
x
là
A.
1
2
C
x
. B.
ln 2xC
. C.
2
1
2
C
x
. D.
1
ln 2
2
xC
.
Lời giải
Áp dụng công thức:
11
d lnx ax b C
ax b a
, ta có
1
d ln 2
2
x x C
x
.
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai?
A.
df x x f x C

. B.
cos d sinx x x C
.
C.
1
d , 1
1
x
x x C
. D.
d ln
xx
a x a a C
01a
.
Lời giải
Ta có
d
ln
x
x
a
a x C
a

01a
nên phương án
d ln
xx
a x a a C
01a
sai.
Câu 14. Tích phân
1
3
0
ed
x
x
bằng
A.
3
1
e
2
. B.
e1
. C.
3
e1
3
. D.
3
e1
.
Lời giải
Ta có
1
11
3
3 3 3
0
00
1 1 e 1
e d e d 3 e
3 3 3
x x x
xx

.
Câu 15. Xét
1
2022
2
0
22I x x dx
, nếu đặt
2
2ux
thì
I
bằng
A.
3
2022
2
u du
. B.
1
2022
0
u du
. C.
3
2022
2
2 u du
. D.
3
2022
2
1
2
u du
.
Lời giải
Trang10
Xét
11
20202 2022
2 2 2
00
2 2 2 2I x x dx x d x

Đặt
2
2ux
. Đổi cận:
02xu
;
13xu
.Khi đó
3
2022
2
I u du
Câu 16. Cho số phức
32zi
. Tìm phần ảo của số phức liên hợp của
z
.
A.
2
. B.
2i
. C.
2
. D.
2i
.
Lời giải
Số phức liên hợp của
z
là
32zi
.
Vậy phần ảo của số phức liên hợp của
z
là
2
.
Câu 17. Cho hai số phức
1
12zi
,
2
26zi
. Tích
12
.zz
bằng
A.
10 2i
. B.
2 12i
. C.
14 10i
. D.
14 2i
.
Lời giải
Ta có
12
. 1 2 2 6 14 2z z i i i
.
Câu 18. Xét hai số phức
1
z
,
2
z
tùy ý. Phát biểu nào sau đây sai?
A.
1 2 1 2
.z z z z
. B.
1 2 1 2
.z z z z
. C.
1 2 1 2
z z z z
. D.
1 2 1 2
z z z z
.
Lời giải
Giả sử
1
z a bi
,
2
z c di
, , ,a b c d
, ta có
22
12
z z a c b d
mà
2 2 2 2
12
z z a b c d
Vậy về tổng quát
1 2 1 2
z z z z
.
Câu 19. Một khối lăng trụ có thể tích bằng
V
, diện tích mặt đáy bằng
S
. Chiều cao của khối lăng trụ
đó bằng
A.
S
V
. B.
3V
S
. C.
V
S
. D.
3
S
V
.
Lời giải
Gọi
h
là chiều cao của khối lăng trụ.
Ta có thể tích khối lăng trụ là
.
V
V S h h
S
.
Câu 20. Cho khối chóp
.S ABC
có đáy là tam giác đều cạnh
a
,
SA ABC
,
SA a
(tham khảo hình
vẽ bên dưới).
Thể tích của khối chóp đã cho bằng:
A.
. B.
. C.
3
3a
. D.
3
3
12
a
.
Trang11
Lời giải
Vì
SA ABC
nên ta có
SA
là đường cao của hình chóp hay
h SA a
.
Do đáy của hình chóp là tam giác đều cạnh
a
nên ta có:
2
3
4
a
S
.
Khi đó thể tích của khối chóp đã cho là:
1
.
3
V S h
23
1 3 3
..
3 4 12
aa
a
(đvtt).
Câu 21. Cho hình nón có bán kính đáy
3R
và độ dài đường sinh
4l
. Tính diện tích xung quanh
xq
S
của hình nón đã cho.
A.
12
xq
S
. B.
43
xq
S
. C.
39
xq
S
. D.
83
xq
S
.
Lời giải
Ta có
xq
S Rl
. Nên
3.4 4 3
xq
S


.
Câu 22. Tính thể tích của khối trụ biết bán kính đáy của khối trụ đó bằng
a
và chiều cao bằng
2a
A.
3
2 a
. B.
3
a
. C.
3
4 a
. D.
2
2 a
.
Lời giải
Thể tích khối trụ là
2 2 3
.2 2 .V r h a a a
Câu 23. Trong không gian với hệ trục tọa độ
Oxyz
, hình chiếu vuông góc của điểm
1;2;3A
trên mặt
phẳng
Oyz
là
A.
0;2;3M
. B.
1;0;3N
. C.
1;0;0P
. D.
0;2;0Q
.
Lời giải
Hình chiếu của điểm
;;M x y z
lên mặt phẳng
Oyz
là
0; ;M y z
Nên
0;2;3M
là hình chiếu của điểm
1;2;3A
trên mặt phẳng
Oyz
.
Câu 24. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
(1; 2 ; 3)A
và mặt phẳng
( ):3 4 7 2 0P x y z
. Đường thẳng đi qua
A
và vuông góc với mặt phẳng
()P
có phương
trình là
A.
3
4 2 ( ).
73
xt
y t t
zt


B.
13
2 4 ( ).
37
xt
y t t
zt


C.
13
2 4 ( ).
37
xt
y t t
zt


D.
14
2 3 ( ).
37
xt
y t t
zt


Lời giải
Trang12
Gọi
u
là véc tơ chỉ phương của đường thẳng
()
thỏa mãn yêu cầu bài toán.
Ta có véc tơ pháp tuyến của mặt phẳng
()P
:
(3; 4;7)
p
n 
.
Vì
13
( ) ( )
(3; 4;7)
( ): 2 4 ( ).
()
(1;2;3) ( )
37
p
xt
P
un
y t t
A
A
zt







Câu 25. Trong không gian với hệ trục tọa độ
Oxyz
, mặt cầu tâm
1;0;0I
và bán kính bằng
2
có
phương trình là
A.
2
22
12x y z
. B.
2
22
12x y z
.
C.
2
22
14x y z
. D.
2
22
14x y z
.
Lời giải
Phương trình mặt cầu có tâm
;;I a b c
và bán kính
R
có dạng:
2 2 2
2
x a y b z c R
Mà tâm
1;0;0I
và bán kính
nên
2
22
1 4.x y z
Câu 26. Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống
nhau, một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp
theo hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là
A.
1
7
. B.
. C.
2
7!
. D.
1
7!
.
Lời giải
Hoán vị 7 chữ cái này ta được 1 dãy 7 chữ cái, tuy nhiên trong đó có 2 chữ T giống nhau nên
khi hoán vị 2 chữ T này cho nhau không tạo dãy mới.
Vì vậy sẽ có:
7!
2!

dãy khác nhau.
Xác suất để tạo thành dãy THPTCLS là
12
7!
7!
2!
P 
.
Câu 27. Cho hình chóp
.S ABC
có đáy là tam giác vuông tại
B
,
3AB a
,
3BC a
;
SA
vuông góc
với mặt phẳng đáy và
2SA a
.Góc giữa đường thẳng
SC
và mặt phẳng đáy
ABC
bằng
A.
ο
60
. B.
ο
45
. C.
ο
30
. D.
ο
90
.
Lời giải
Ta có
SA ABC
nên góc giữa
SC
và
ABC
bằng
ACS
.
2 2 2 2
9 3 2 3AC AB BC a a a
.
Trang13
Suy ra
21
tan
2 3 3
SA a
ACS
AC
a
ο
30ACS
.
Câu 28. Cho hàm số bậc bốn
y f x
. Hàm số
y f x
có đồ thị như hình vẽ sau
Hàm số
y f x
nghịch biến trên khoảng nào trong các khoảng sau?
A.
1;4
. B.
1;1
. C.
0;3
. D.
;0
.
Lời giải
Dựa vào đồ thị hàm số
y f x
ta có
0 1;1 4;f x x
và
0 ; 1 1;4f x x

.
Do đó hàm số
y f x
đồng biến trên các khoảng
1;1
và
4;
, nghịch biến trên các
khoảng
;1
và
1;4
.
Vậy hàm số
y f x
nghịch biến trên khoảng
1;4
là đng.
Câu 29. Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: nếu trên mỗi
mét vuông mặt hồ thả
x
con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là
2
108 x
(gam). Hỏi nên thả bao nhiêu con tôm giống trên mỗi mét vuông mặt hồ tự nhiên đó để
cuối vụ thu hoạch được nhiều tôm nhất.
A.6. B.7. C.8. D.9.
Lời giải
Sau một vụ lượng tôm trung bình trên mỗi
2
m
mặt hồ nặng
23
108 108 ( )x x x x gam
Xét hàm số
3
( ) 108f x x x
trên khoảng
(0; )
ta có
22
6
'( ) 108 3 ; '( ) 0 108 3 0
60
x
f x x f x x
x
Trên khoảng
(0; )
hàm số
3
( ) 108f x x x
đạt GTLN tại
6x
.
Vậy nên thả 6 con tôm giống trên mỗi mét vuông mặt hồ thì cuối vụ thu hoạch được nhiều tôm
nhất.
Câu 30. Xét tất cả các số dương
a
và
b
thỏa mãn
3 3 9
log log loga b ab
. Tính giá trị của
ab
.
A.
1ab
. B.
2ab
. C.
1
2
ab
. D.
0ab
.
Lời giải
Trang14
Ta có:
2
3 3 9 3 3 3
3
1
log log log log log log log
2
a b ab ab ab ab ab
3
1
log 0 1.
2
ab ab
Câu 31. Tích tất cả các nghiệm của phương trình
2
2 5 4
24
xx
bằng
A.
1
. B.
2
. C.
2
. D.
1
.
Lời giải
Ta có:
22
2 5 4 2 5 4 2 2 2
1
2 4 2 2 2 5 4 2 2 5 2 0
2
2
x x x x
x
x x x x
x


.
Vậy tích các nghiệm của phương trình là
1
.
Câu 32. Số nghiệm nguyên của bất phương trình
2
3x
52
1
5
5
x



là
A.
3
. B.
1
. C.
2
. D.
4
.
Lời giải
Bất phương trình
2
2
3
5 2 3 5 2 2
1
5 5 5 3 5 2
5
x
x x x
xx




2
1
3 5 2 0 2
3
x x x
.
Vì
x
nên
0;1x
. Vậy bất phương trình có
2
nghiệm nguyên.
Câu 33. Cho hàm số
fx
liên tục trên đoạn
0;1
,có đạo hàm
fx
thỏa mãn
1
0
2 1 d 10x f x x

và
0 3 1ff
. Tính
1
0
dI f x x
.
A.
5I 
. B.
2I 
. C.
2I
. D.
5I
.
Lời giải
Đặt:
2 1 d 2du x u x
,
ddv f x x
chọn
v f x
.
Ta co
:
1
0
2 1 d 10x f x x

1
0
1
2 1 2 d 10
0
x f x f x x
1
0
3 1 0 2 d 10f f f x x
1
0
0 2 d 10f x x
1
0
d5f x x
.
Câu 34. Tìm số phức
z
thỏa mãn
2 9 2z z i
.
A.
32zi
. B.
3zi
. C.
32zi
. D.
23zi
.
Lời giải
Đặt
,z a bi a b R
.
Theo giả thiết ta có
2 9 2a bi a bi i
.
Điều này tương đương với
3 9 2 0a b i
.
Từ đây ta được
3 9 2 0ab
.
Như vậy
3a
và
2b 
.
Tức là
32zi
.
Trang15
Câu 35. Trong không gian với hệ trục tọa độ
Oxyz
, cho đường thẳng
21
:
3 1 2
x y z
. Gọi
M
là
giao điểm của
với mặt phẳng
: 2 3 2 0P x y z
. Tọa độ điểm
M
là
A.
2;0; 1M
. B.
5; 1; 3M 
. C.
1;0;1M
. D.
1;1;1M
.
Lời giải
Tọa độ của điểm
M
là nghiệm của hệ:
2
31
1
12
2 3 2 0
xy
yz
x y z
32
21
2 3 2
xy
yz
x y z

1
1
1
x
y
z


Vậy
1;1;1M
.
Câu 36. Trong không gian với hệ trục tọa độ
Oxyz
,
P
là mặt phẳng đi qua điểm
1;2;3M
và cắt các
tia
,,Ox Oy Oz
lần lượt tại
,,A B C
(khác gốc tọa độ
O
) sao cho
M
là trực tâm tam giác
ABC
.
Biết mặt phẳng
P
có phương trình
14 0ax by cz
. Tính tổng
T a b c
.
A.8. B.14. C.6. D.11.
Lời giải
Ta có tứ diện
OABC
là tứ diện vuông tại
O
, mà
M
là trực tâm tam giác
ABC
nên
OM ABC OM P
.
Vậy
1;2;3OM
là một véc tơ pháp tuyến của mặt phẳng
P
và
P
đi qua
M
nên
P
có
phương trình:
2 3 14 0 6x y z T a b c
.
Câu 37. Trong không gian với hệ trục tọa độ
Oxyz
, cho điểm
7; 1;2A
và mặt phẳng
: 2 2 6 0P x y z
. Mă
t câu
S
tâm
A
và tiếp xc với mặt phẳng
P
có phương trình
là
A.
2 2 2
49
7 1 2
9
x y z
. B.
2 2 2
7
7 1 2
3
x y z
.
C.
2 2 2
49
7 1 2
9
x y z
. D.
2 2 2
7
7 1 2
3
x y z
.
Lời giải
Mă
t câu
S
tâm
A
và tiếp xc với mặt phẳng
P
có bán kính là
2
22
7 2. 1 2.2 6
7
,
3
1 2 2
R d A P
.
Vâ
y mă
t câu
S
có phương trình là
2 2 2
49
7 1 2
9
x y z
.
Câu 38. Cho hình lăng trụ đứng
. ' ' 'ABC A B C
có đáy
ABC
là tam giác đều cạnh
a
. Cạnh
'3BA a
.
Khoảng cách giữa hai đường thẳng
'AB
và
'BC
là:
A.
2a
. B.
3
a
.
C.
2
3
a
. D.
2
3
a
.
Lời giải.
Trang16
'2AA a
Gọi
M
là trung điểm
AC
,
''E AB A B E
là trung điểm của
'AB
Khi đó
' / / ' / / 'B C ME B C A BM
' , ' ' , ' , ' , 'd B C A B d B C A BM d C A BM d A A BM
(*)
Trong mặt phẳng
':A AM
kẻ
'AH A M
(1)
Do
ABC
đều
BM AC
. ' ' 'ABC A B C
là hình lăng trụ đứng
''AA ABC AA BM
Nên
'BM A AM BM AH
(2)
Từ (1) và (2)
' , 'AH A BM d A A BM AH
(**)
Trong tam giác
'A AM
vuông tại
A
,
AH
là đường cao:
2 2 2 2 2 2
1 1 1 1 4 9 2
' 2 2 3
a
AH
AH A A AM a a a
(***)
Từ (*), (**), (***)
2
' , '
3
a
d A B B C
.
Câu 39. Gọi là tập hợp tất cả các giá trị thực của tham số để đồ thị của hàm số
có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ
tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của .
A.
2
. B.
1
5
. C.
1
5
. D.
2
.
Lời giải
Để hàm số có ba điểm cực trị thì phải có ba nghiệm phân biệt.
Ta có . , .
Ba điểm cực trị là .
H
M
B'
B
A'
C'
C
E
A
S
m
C
4 2 2 4
25y x m x m
O
S
4 2 2 4
25y x m x m
'0y
3 2 2 2
' 4 4 4y x m x x x m
0
'0
x
y x m
xm

0m
4
0; 5 , ;5 , ;5A m B m C m
Trang17
Ba điểm và gốc tọa độ tạo thành tứ giác nội tiếp khi và chỉ khi
, (do ) . Vậy có 2 phần tử và
có tích bằng
1
5
.
Câu 40. Gọi
S
là tập nghiệm của bất phương trình
22
log 2 log 2 3
aa
x x x x
. Biết
;S m n
và
7
3
thuộc
S
, tính
mn
.
A.
13
3
mn
. B.
7
2
mn
. C.
11
3
mn
. D.
9
2
mn
.
Lời giải
Điều kiện:
2
2
20
23
2 3 0 .
01
01
xx
x
xx
a
a




Do
7
3
x
là nghiệm của bất phương trình đã cho nên
10 20
log log 0 1.
99
aa
a
Vì
01a
nên bất phương trình
22
2 2 3x x x x
23
2
55
2 3 5 0 1 2 .
22
x
x x x x

Vì vậy
59
2
22
mn
Câu 41. Cho hàm số
y f x
liên tục trên đoạn
0;
2



thỏa mãn:
2cos . 1 4sin sin2 . 3 2cos2 sin4 4sin2 4cosx f x x f x x x x
,
0;
2
x




.
Khi đó
5
1
I f x dx
bằng
A.2. B.0. C.
8
. D.
16
.
Lời giải
Ta có:
2cos . 1 4sin sin2 . 3 2cos2 sin4 4sin2 4cos (*)x f x x f x x x x
Lấy tích phân từ
0
đến
2
hai vế của
(*)
ta được:
2 2 2
0 0 0
2cos . 1 4sin sin2 . 3 2cos2 sin4 4sin2 4cosx f x dx x f x dx x x x dx
,,A B C
0;0O
BC
2
BC
BC
.0BABO
24
50mm
2
1
5
m
S
Trang18
22
00
5 5 5 5
1 1 1 1
11
1 4sin (1 4sin ) 3 2cos2 (3 2cos2 ) 0
24
11
0 0 0
24
f x d x f x d x
f t dt f t dt f t dt f x dx


Vậy
5
1
I f x dx
= 0.
Câu 42. Có bao nhiêu số phức
z
thỏa mãn
1 2 2zi
và
4 4 10zz
?
A.
1
. B.
0
. C.
2
. D.
4
.
Lời giải
Áp dụng các tính chất
1 2 1 2
;z z z z z z
ta có
4444zzzz
.
Do đó
4 4 10 4 4 10z z z z
.
Gọi
M
là điểm biểu diễn của
z
.
Do
1 2 2zi
nên
M
thuộc đường tròn
C
tâm
1;2I
, bán kính
2R
.
C
có phương
trình là
22
1 2 4xy
.
Do
4 4 10zz
nên
M
thuộc đường elip
E
có hai tiêu điểm là
1
4;0F
2
; 4;0F
và
có độ dài trục lớn là
10
.
E
có phương trình là
22
1
25 9
xy

.
Từ đây có
M
là giao điểm của
C
và
E
.
Từ hình vẽ của
C
và
E
ta thấy chúng có
2
giao điểm nên có
2
số phức thỏa mãn yêu cầu.
Câu 43. Cho hình chóp
.S ABC
có đáy là tam giác đều cạnh bằng
a
, tam giác
SAB
cân tại
S
và thuộc
mặt phẳng vuông góc với mặt phẳng
ABC
, góc giữa hai mặt phẳng
SCA
và
SCB
bằng
0
60
. Gọi
H
là trung điểm của đoạn
AB
. Trong các mệnh đề sau, mệnh đề nào đng:
A.Thể tích khối chóp
.S ABC
bằng
3
2
16
a
. B.Thể tích khối chóp
.B SHC
bằng
3
2
16
a
.
C.Thể tích khối chóp
.S AHC
bằng
3
2
64
a
. D.Không tồn tại hình chóp đã cho.
Lời giải
Trang19
Tam giác
SAB
thuộc mặt phẳng vuông góc với mặt phẳng
ABC
SH ABC
, từ đó suy
ra đường cao của hình chóp
.S AHC
là
SH
Kẻ
AK SC SC AKB
SC KB
0
; ; 60SAC SBC KA KB
0
0
60
120
AKB
AKB
Nếu
0
60AKB
thì dễ thấy
KAB
đều
KA KB AB AC
(vô lí). Vậy
0
120AKB
khi đó
KAB
cân tại
K
và
0
60AKH
0
tan60
23
AH a
KH
Trong
SHC
vuông tại
H
ta có
2 2 2
1 1 1
KH HC HS

thay
23
a
KH
và
3
2
a
HC
vào ta được
6
8
a
SH
. Vậy
6
8
a
h
.
3
.
1 1 6 1 3 2
. . . . . .
3 3 8 2 2 2 64
S AHC AHC
a a a a
V SH dt
.
Câu 44. Một cái bình thủy tinh có phần không gian bên trong là một hình nón có đỉnh hướng xuống
dưới theo chiều thẳng đứng. Rót nước vào bình cho đến khi phần không gian trống trong bình
có chiều cao 2 cm. Sau đó đậy kín miệng bình bởi một cái nắp phẳng và lật ngược bình để đỉnh
hướng lên trên theo chiều thẳng đứng, khi đó mực nước cao cách đỉnh của nón 8 cm (hình vẽ
minh họa bên dưới).
Biết chiều cao của nón là
h a b
cm. Tính
T a b
.
A.
22
. B.
58
. C.
86
. D.
72
.
Lời giải
8 cm
2 cm
Trang20
Để ý rằng có 3 hình nón đồng dạng: Phần không gian bên trongbình thủy tinh (có thể tích
V
),
phần không chứa nước khi đặt bình có đỉnh hướng lên (có thể tích
1
V
), phần chứa nước khi đặt
bình có đỉnh hướng xuống (có thể tích
2
V
). Do tỷ số đồng dạng bằng với tỷ số của chiều cao và
tỷ số thể tích là lập phương tỷ số đồng dạng nên ta có
3
33
12
3
3 3 3
12
2
512
;;
8
2
hV
V h V h V
VV
V V h h
h
. Mà
12
V V V
nên ta có:
3
3 2 3 2
33
2
512
512 6 12 8 2 84 0 1 85
hV
V
V h h h h h h h
hh
Vậy
86T
Câu 45. Trong không gian với hệ trục tọa độ
Oxyz
cho điểm
1;0;0I
, điểm
7 4 4
;;
999
M



và đường
thẳng
2
:
1
x
d y t
zt

.
,,N a b c
là điểm thuộc đường thẳng
d
sao cho diện tích tam giác
IMN
nhỏ nhất. Khi đó
abc
có giá trị bằng:
A.
2
. B.
2
. C.
5
2
. D.
5
2
.
Lời giải
Ta có
2
3
IM
.
Gọi
H
là hình chiếu của
N
trên đường thẳng
'd
đi qua
,IM
, ta có:
11
.
23
IMN
S IM NH NH

Diện tích tam giác
IMN
nhỏ nhất khi và chỉ khi độ dài
NH
nhỏ nhất.
2; ;1N d N n n
1; ;1IN n n
.
Đường thẳng
'd
có vecto chỉ phương
' 1; 2; 2u

.
, ' 2; 3; 2IN u n n


.
2
22
2
59
2
,'
2 3 2
24
1
;'
3 3 2
'
n
IN u
nn
NH d N d
u





.
Dấu
xảy ra khi
5
2
n 
, suy ra:
53
2; ;
22
N




.Vậy
2abc
.
Câu 46. Cho hàm số
4 3 2
2 1 2 2022f x x x m x x m
, với
m
là tham số. Có bao nhiêu giá
trị nguyên của
m
thuộc đoạn
2021;2022
để hàm số
2021 2022y f x
có số điểm
cực trị nhiều nhất?
A.2021. B.2022. C.4040. D.2023
Lời giải
Hàm số
2021 2022y f x
có số điểm cực trị nhiều nhất là
7
khi và chỉ khi phương
trình
2021 2022fx
có
4
nghiệm phân biệt hay phương trình
2022fx
có
4
nghiệm
phân biệt
Ta có
4 3 2
2 1 2 02022f x m x mx xx
Trang21
2
2
1
1 1 2 0 1
2 0 *
x
x x x x m x
x x m



Suy ra
2022fx
có
4
nghiệm phân biệt khi và chỉ khi
*
có
2
nghiệm phân biệt khác
1
và 1tức là
2
2
1 2 0
3
1 2 0
10
1
m
m
m
m
m

do
m
nguyên thuộc
2021;2022
nên có 2021 giá trị thỏa mãn.
Câu 47. Có bao nhiêu số nguyên dương
m
để phương trình
2
1 .ln( 1) 2 1
x x x
m e mx e e
có
2
nghiệm phân biệt không lớn hơn 5.
A.26. B.27. C.29. D.28.
Lời giải
Xét phương trình
2
1 .ln( 1) 2 1
x x x
m e mx e e
(*) điều kiện
10mx 
10
1.
*
ln( 1)
x
x
e
e m mx

1 0 0
x
ex
1 .ln( 1)
x
e m mx
, Đặt
ln( 1) 1 .
x
y mx e my
Ta có hệ phương trình
ln( 1)(1)
ln( 1)(2)
x my
y mx


Trừ (1) và (2) theo vế ta được:
ln( 1) ln( 1)x y my mx
hay
ln( 1) ln( 1)x mx y my
với
0m
thì hàm số
( ) ln( 1)f x x mx
đồng biến trên tập xác định nên
ln( 1) ln( 1)x mx y my x y
Thay
xy
vào
(1)
ta được
ln( 1)x mx
hay
1(4)
x
e mx
Rõ ràng
0x
là 1 nghiệm của phương trình (4).
Với
0x
ta có
1
(4)
x
e
m
x

Xét hàm số
1
()
x
e
gx
x
, ta có: Tập xác định
\{0}D
và
2
1
()
xx
xe e
gx
x

( ) 0 1 0
xx
g x xe e
Hàm số
( ) 1
xx
h x xe e
có
()
x
h x xe
nên
( ) 0 0h x x
Ta có bảng biến thiên của
()hx
như sau:
Suy ra
( ) 0 ,h x x
do đó
( ) 0 , 0g x x
Bảng biến thiên của
()gx
:
Trang22
Để phương trình
1 ln( 1)
xm
e mx
có 2 nghiệm phân biệt không lớn hơn 5 thì phương trình
()m g x
có duy nhất 1 nghiệm bé hơn hoặc bằng 5. Ta có
5
1
(5) 29,5
5
e
g

Dựa vào bảng biến thiên của
()gx
ta có
0 (5)
1
mg
m

do
*
m
nên có 28 giá trị thỏa mãn.
Câu 48. Cho hàm số
fx
với đồ thị là Parabol đỉnh
I
có tung độ bằng
7
12
và hàm số bậc ba
gx
.
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ
1 2 3
,,x x x
thoả mãn
1 2 3
18 55x x x 
(hình vẽ).
Diện tích miền tô đậm gần số nào nhất trong các số sau đây?
A.5,7. B.5,9. C.6,1. D.6,3.
Lời giải
Dễ thấy
17
,
2 12
I



và
7
12
27
f x x x
.
Hàm số
gx
đạt cực trị tại
1, 2xx
nên
32
' 1 2 2
32
xx
g x a x x a x bgx



Đồ thị hàm số
gx
đi qua
I
nên
1 7 7 13
,
2 12 12 12
g a b



1
.
Phương trình hoành độ giao điểm:
32
7
2 1 2
3 2 27
xx
f x g x a x b x x



Theo định lý viet ta có:
1 2 3
14
28 55
27
18 55 18. 55 18 ,
33
3
b
a
x x x b
a
2
Trang23
Từ
1
,
2
ta được
32
11
1, 2
2 3 2 2
xx
a b g x x
. Từ đó suy ra diện tích miền tô
đậm sấp sỉ 5,7.
Câu 49. Cho
,,M N P
lần lượt là các điểm biểu diễn số phức
1
z
,
2
z
,
3
z
thỏa mãn điều kiện
11
5 9 3 5z i z
,
22
23z z i
,
33
1 3 4zz
. Khi
,,M N P
không thẳng hàng,
giá trị nhỏ nhất của nửa chu vi
p
của tam giác
là
A.
10 5
9
. B.
65
5
. C.
9 10
10
. D.
5 11
13
.
Lời giải
Trong mặt phẳng
Oxy
, gọi
1;0A
,
0;3B
,
3;0C
và
,,M N P
lần lượt là các điểm biểu
diễn số phức
1
z
,
2
z
,
3
z
. Ta có
Tập hợp điểm
M
biểu diễn số phức
1
z
là đường thẳng
AB
.
Tập hợp điểm
N
biểu diễn số phức
2
z
là đường thẳng
BC
.
33
1 3 4zz
PA PC AC
Tập hợp điểm
P
biểu diễn số phức
3
z
là đoạn
AC
.
Khi đó
2
MN NP PM
p

.
Gọi
1
P
,
2
P
lần lượt đối xứng với
P
qua
AB
,
BC
. Ta có
1
MP MP
,
2
NP NP
.
Khi đó
1 2 1 2
MN NP PM PM MN NP PP
.
Ta thấy
1 2 1 2
2PBP PBA ABC CBP PBA ABC PBC ABC
.
Theo định lí Sin:
sin 2 5
sin
5
sin sin
AB AC AC BCA
ABC
AB
BCA ABC
Gọi
H
là trung điểm của
12
PP
, khi đó
1 2 2 2 2
2 5 4 5 4 5 12 5
2 2 .sin 2 .sin 2 .
5 5 5 5
PP P H BP P BH BP ABC BP BP BO
.
Vậy giá trị nhỏ nhất của
p
là
65
5
.
Câu 50. Trong không gian với hệ trục tọa độ
Oxyz
, cho
3
đường thẳng
1
d
,
2
d
,
3
d
có phương
trình
1
11
1
12
:1
12
xt
d y t
zt



,
2
22
2
3
: 1 2
22
xt
d y t
zt


,
3
33
3
42
: 4 2
1
xt
d y t
zt



.
;S I R
là mặt cầu tâm
I
bán
Trang24
kính
R
tiếp xúc với
3
đường thẳng đó. Giá trị nhỏ nhất của
R
gần số nào nhất trong các số
sau:
A.2,1. B.2,2. C.2,3. D.2,4.
Lời giải
Ta có:
1
d
đi qua điểm
1;1;1A
có VTCP
1
2;1; 2u 

.
2
d
đi qua điểm
3; 1;2B
có VTCP
2
1;2;2u
.
3
d
đi qua điểm
4;4;1C
có VTCP
3
2; 2;1u 
.
Ta có
12
.0uu
,
23
.0uu
,
31
.0uu
1
d
,
2
d
,
3
d
đôi một vuông góc với nhau.
12
, . 0u u AB


,
23
, . 0u u BC


,
31
, . 0u u CA


1
d
,
2
d
,
3
d
đôi một chéo nhau.
Lại có:
2; 2;1AB 
;
1
.0AB u
và
2
.0AB u
nên
1
d
,
2
d
,
3
d
chứa
3
cạnh của hình
hộp chữ nhật như hình vẽ.
Vì mặt cầu tâm
;;I a b c
tiếp xúc với
3
đường thẳng
1
d
,
2
d
,
3
d
nên bán kính
1 2 3
, , ,R d I d d I d d I d
2 2 2 2
1 2 3
, , ,R d I d d I d d I d
2
1
2
1
,AI u
R
u









2
2
2
,BI u
u







2
3
3
,CI u
u







, ta thấy
2 2 2
1 2 3
9u u u
và
1; 1; 1AI a b c
,
1
, 2 3;2 2 4; 2 1AI u b c a c a b


.
3; 1; 2BI a b c
,
2
, 2 2 6; 2 4;2 7BI u b c a c a b


.
4; 4; 1CI a b c
,
3
, 2 6; 2 2; 2 2 16CI u b c a c a b


.
2 2 2
2
1 2 3
9 , , ,R AI u BI u CI u
2 2 2
2
1 2 3
27 , , ,R AI u BI u CI u
2 2 2
18 126 54 54 423a b c a b c
2 2 2
7 3 3 243 243
18 18 18
2 2 2 2 2
abc
min
32
2
R
khi đó
2,12R
.
B
C
d
1
d
2
A
d
3
I
| 1/24
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT THANH HÓA
KỲ THI KSCL CÁC MÔN THI TN THPT NĂM 2022 - LẦN 2
TRƯỜNG THPT CHUYÊN LAM SƠN Môn thi: Toán Ngày thi: 03/04/2022 ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 90 phút, không kể thời gian phát đề
( Đề thi có 06 trang)
Họ và tên: ............................................................................ Số báo danh: ............. Mã đề Gốc Câu 1.
Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập A  2, 3, 4, 5,  6 A. 4 C . B. 4 C . C. 4 A . D. 4 A . 5 6 5 6 Câu 2.
Cho cấp số nhân u với u  8 và u  4 . Công bội của cấp số nhân đã cho bằng n  1 2 1 1 A. . B.  . C. 2  . D. 2 . 2 2 Câu 3.
Hàm số nào sau đây đồng biến trên  ? x 1 A. 3
y x  3x . B. 3
y x  3x . C. y
y x x  . x  . D. 4 2 3 1 1 Câu 4.
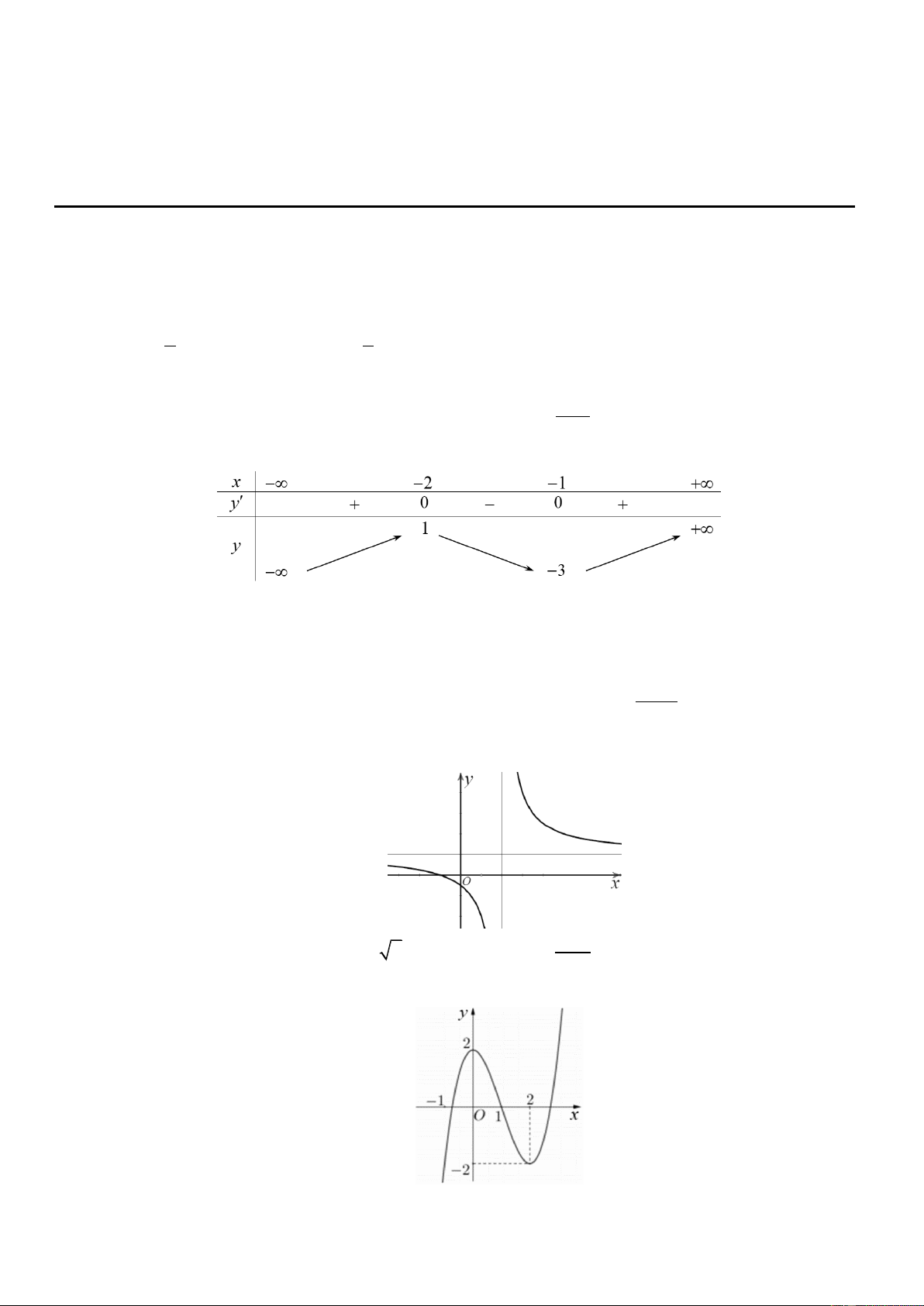
Cho hàm số y f x có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm A. x  3  . B. x  1  .
C. x 1. D. x  2  . Câu 5. Hàm số 4 2
y x x  3 có mấy điểm cực trị? A.1 . B. 2 . C. 3 . D. 0 . 5x 1 Câu 6.
Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y x ? 2
A. y  5 .
B. x  5.
C. x  2 . D. x  2  . Câu 7.
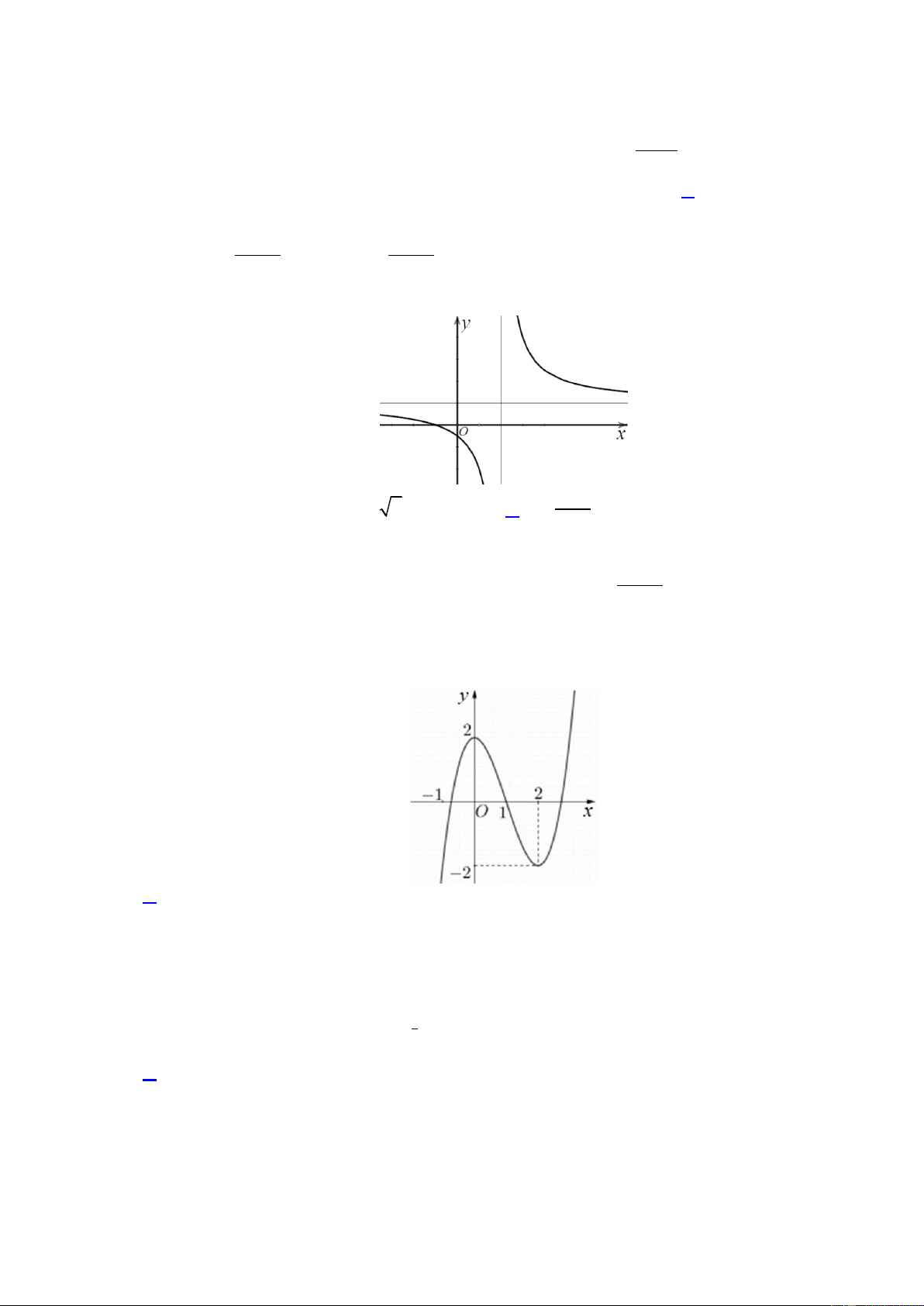
Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây? x 1 A. 3 2
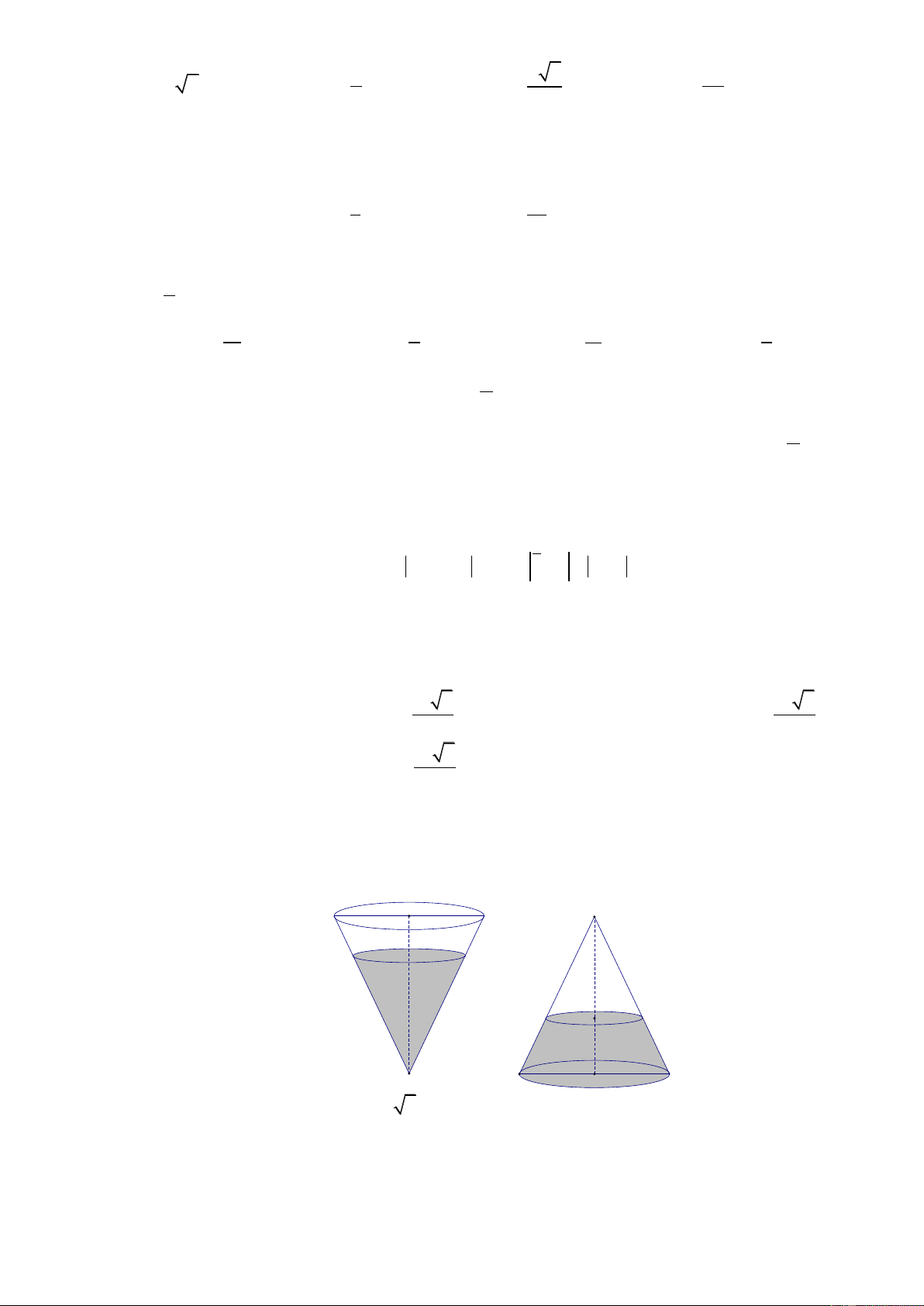
y x x x 1 . B. y x . C. y y  log x . x  . D. 2 3 Câu 8.
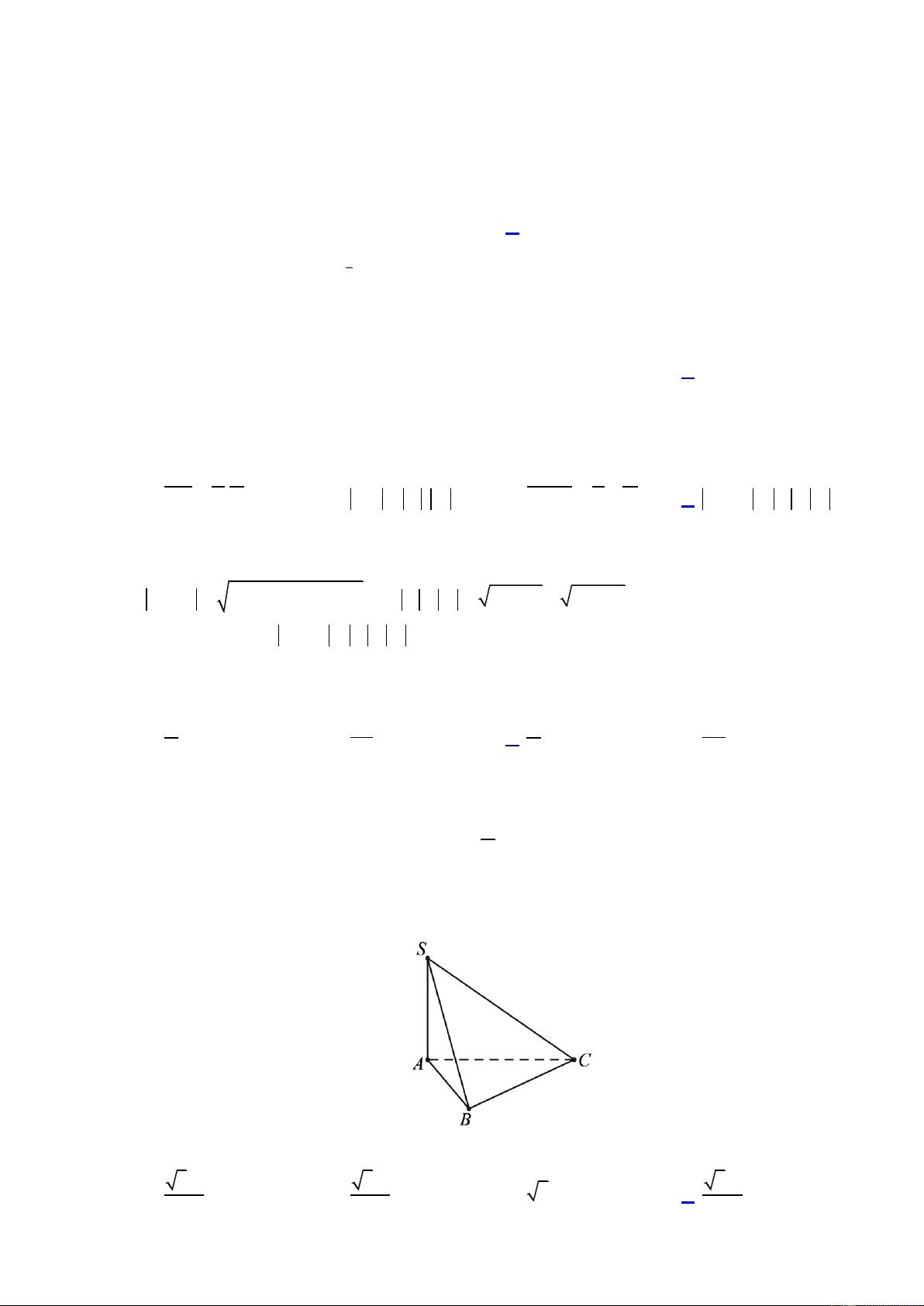
Cho hàm số bậc ba y f x có đồ thị như hình vẽ dưới đây. Trang1
Số nghiệm của phương trình f x  1là: A.3. B.0. C.2. D.1. Câu 9.
Tập xác định của hàm số y   x  35 1 là
A. 1;  .
B. 0;  . C.1; . D.  \   1 . Câu 10. Hàm số   4 2x f x   có đạo hàm là xx
A. f  xx4  2 .ln 2.
B. f  xx4
 4.2 .ln 2. C. f  x 4 2  .
D. f  x 4 4.2  . ln 2 ln 2
Câu 11. Tập nghiệm của phương trình log  x  
1  log 2x  3  0 là  2  A.  4;   . B.  2  . C.  4  . D.  . 3  1
Câu 12. Trên khoảng ;  2 , họ nguyên hàm của hàm số f (x)  x  là 2 1 1  1 A.C x   C . C.C . D.
ln x  2  C . x  . B. ln 2 2 x  22 2
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai? A. f
 xdx f xC . B. cos d
x x  sin x C  .  1   x
C. x dx   C,    1  x x       . D. a dx a ln a C  0 a  1 . 1 1 Câu 14. Tích phân 3 e xdx  bằng 0 1 3 e 1 A. 3 e  . B. e 1. C. . D. 3 e 1 . 2 3 1 2022
Câu 15. Xét I  2x
  2x 2 dx, nếu đặt 2
u x  2 thì I bằng 0 3 1 3 3 1 A. 2022 u du  . B. 2022 u du  . C. 2022 2 u du  . D. 2022 u du  . 2 2 0 2 2
Câu 16. Cho số phức z  3 2i . Tìm phần ảo của số phức liên hợp của z . A. 2  . B. 2i . C. 2 . D. 2  i .
Câu 17. Cho hai số phức z  1 2i , z  2  6i . Tích z .z bằng 1 2 1 2 A. 1  0 2i .
B. 2 12i . C.14 10i . D.14  2i .
Câu 18. Xét hai số phức z , z tùy ý. Phát biểu nào sau đây sai? 1 2
A. z z z .z .
B. z z z . z .
C. z z z z .
D. z z z z . 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2
Câu 19. Một khối lăng trụ có thể tích bằng V , diện tích mặt đáy bằng S . Chiều cao của khối lăng trụ đó bằng S 3V V S A. . B. . C. . D. . V S S 3V
Câu 20. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a , SA   ABC  , SA a (tham khảo hình vẽ bên dưới). Trang2
Thể tích của khối chóp đã cho bằng: 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 4 6 12
Câu 21. Cho hình nón có bán kính đáy R  3 và độ dài đường sinh l  4 . Tính diện tích xung quanh
S của hình nón đã cho. xq A. S 12 . B. S  4 3 . C. S  39 . D. S  8 3 . xq xq xq xq
Câu 22. Tính thể tích của khối trụ biết bán kính đáy của khối trụ đó bằng a và chiều cao bằng 2a A. 3 2 a . B. 3  a . C. 3 4 a . D. 2 2 a .
Câu 23. Trong không gian với hệ trục tọa độ Oxyz , hình chiếu vuông góc của điểm A1; 2;3 trên mặt phẳng Oyz là
A. M 0; 2;3 .
B. N 1;0;3 .
C. P 1;0;0 .
D. Q 0; 2;0 .
Câu 24. Trong không gian với hệ trục tọa độ Oxyz , cho điểm (
A 1 ; 2 ; 3) và mặt phẳng
(P) : 3x  4 y  7z  2  0 . Đường thẳng đi qua A và vuông góc với mặt phẳng (P) có phương trình là x  3 tx 1 3t   A. y  4
  2t (t  ).
B. y  2  4t (t   ).   z  7  3tz  3  7t  x 1 3tx 1 4t  
C. y  2  4t (t   ).
D. y  2  3t (t   ).   z  3  7tz  3  7t
Câu 25. Trong không gian với hệ trục tọa độ Oxyz , mặt cầu tâm I 1;0;0 và bán kính bằng 2 có phương trình là
A. x  2 2 2
1  y z  2 .
B. x  2 2 2
1  y z  2 .
C. x  2 2 2
1  y z  4 .
D. x  2 2 2
1  y z  4 .
Câu 26. Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống
nhau, một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp
theo hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là 1 1 2 1 A. . B. . D. . 7 2  . C. 6! 7! 7!
Câu 27. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB  3a , BC  3a ; SA vuông góc
với mặt phẳng đáy và SA  2a . Góc giữa đường thẳng SC và mặt phẳng đáy  ABC  bằng A. ο 60 . B. ο 45 . C. ο 30 . D. ο 90 .
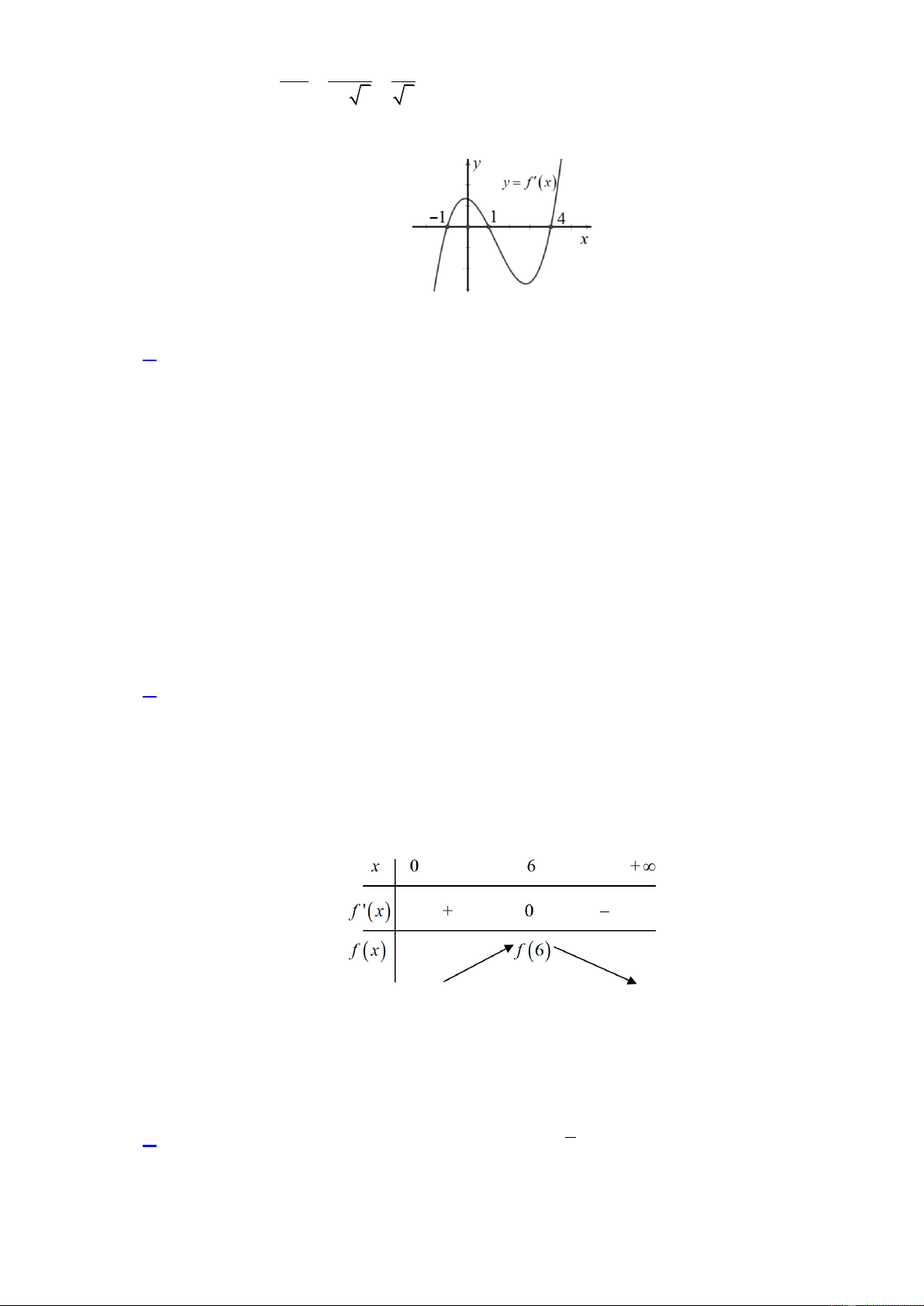
Câu 28. Cho hàm số bậc bốn y f x . Hàm số y f  x có đồ thị như hình vẽ như sau Trang3
Hàm số y f x nghịch biến trên khoảng nào trong các khoảng sau? A. 1;4 . B. 1;  1 . C. 0;3 . D. ;0 .
Câu 29. Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: nếu trên mỗi
mét vuông mặt hồ thả x con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là 2
108  x (gam). Hỏi nên thả bao nhiêu con tôm giống trên mỗi mét vuông mặt hồ tự nhiên đó để
cuối vụ thu hoạch được nhiều tôm nhất. A.6. B.7. C.8. D.9.
Câu 30. Xét tất cả các số dương a và b thỏa mãn log a  log b  log
ab . Tính giá trị của ab . 3 3 9   1
A. ab 1.
B. ab  2 . C. ab  .
D. ab  0 . 2
Câu 31. Tích tất cả các nghiệm của phương trình 2 2x 5x4 2  4 bằng A.1 . B. 2  . C. 2 . D. 1. 2 3x  1 
Câu 32. Số nghiệm nguyên của bất phương trình 5 x2  5   là  5  A. 3 . B.1 . C. 2 . D. 4 . 1
Câu 33. Cho hàm số f x liên tục trên đoạn 0; 
1 ,có đạo hàm f  x thỏa mãn 2x  
1 f  xdx  10 0 1
và f 0  3 f   1 . Tính I f
 xdx . 0 A. I  5  .
B. I  2 .
C. I  2 . D. I  5 .
Câu 34. Tìm số phức z thỏa mãn z  2z  9  2i .
A. z  3 2i .
B. z  3 i .
C. z  3 2i .
D. z  2  3i . x  2 y z 1
Câu 35. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng  :    . Gọi M là 3 1 2
giao điểm của  với mặt phẳng P : x  2y 3z  2  0 . Tọa độ điểm M là
A. M 2;0;   1 .
B. M 5; 1; 3 . C. M 1;0  ;1 . D. M  1  ;1  ;1 .
Câu 36. Trong không gian với hệ trục tọa độ Oxyz ,  P là mặt phẳng đi qua điểm M 1; 2;3 và cắt các
tia Ox, Oy, Oz lần lượt tại ,
A B, C (khác gốc tọa độ O ) sao cho M là trực tâm tam giác ABC .
Biết mặt phẳng  P có phương trình ax by cz 14  0 . Tính tổng T a b c . A.8. B.14. C.6. D.11.
Câu 37. Trong không gian với hệ trục tọa độ Oxyz , cho điểm A7; 1; 2 và mặt phẳng
P: x 2y  2z 6  0 . Mă ̣t cầu S tâm A và tiếp xúc với mặt phẳng P có phương trình là 2 2 2 49 2 2 2 7
A. x  7   y  
1   z  2  .
B. x  7   y  
1   z  2  . 9 3 2 2 2 49 2 2 2 7
C. x  7   y  
1   z  2  .
D. x  7   y  
1   z  2  . 9 3
Câu 38. Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác đều cạnh a . Cạnh BA'  a 3 .
Khoảng cách giữa hai đường thẳng A ' B và B 'C là: Trang4 a a 2 2a A. a 2 . B. . C. . D. . 3 3 3
Câu 39. Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị C của hàm số 4 2 2 4
y x  2m x m  5 có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ O
tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của S . 1 1 A. 2 . B. . C. . D. 2  . 5 5
Câu 40. Gọi S là tập nghiệm của bất phương trình
 2x x    2 log 2 log
x  2x  3 . Biết S  m;na a  7 và
thuộc S , tính m n . 3 13 7 11 9
A. m n  .
B. m n  .
C. m n  .
D. m n  . 3 2 3 2   
Câu 41. Cho hàm số y f x liên tục trên đoạn 0;   thỏa mãn:  2     2cos .
x f 1 4sin x  sin 2 .
x f 3  2cos 2x  sin 4x  4sin 2x  4cos x , x   0;   .  2  5 Khi đó I f
 xdxbằng 1 A.2. B.4. C. 8 . D.16 .
Câu 42. Có bao nhiêu số phức z thỏa mãn z 1 2i  2 và z  4  z  4  10 ? A.1 . B. 0 . C. 2 . D. 4 .
Câu 43. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , tam giác SAB cân tại S và thuộc
mặt phẳng vuông góc với mặt phẳng  ABC  , góc giữa hai mặt phẳng SCA và SCB bằng 0
60 . Gọi H là trung điểm của đoạn AB . Trong các mệnh đề sau, mệnh đề nào đúng: 3 a 2 3 a 2
A.Thể tích khối chóp S.ABC bằng .
B.Thể tích khối chóp . B SHC bằng . 16 16 3 a 2
C.Thể tích khối chóp S.AHC bằng .
D.Không tồn tại hình chóp đã cho. 64
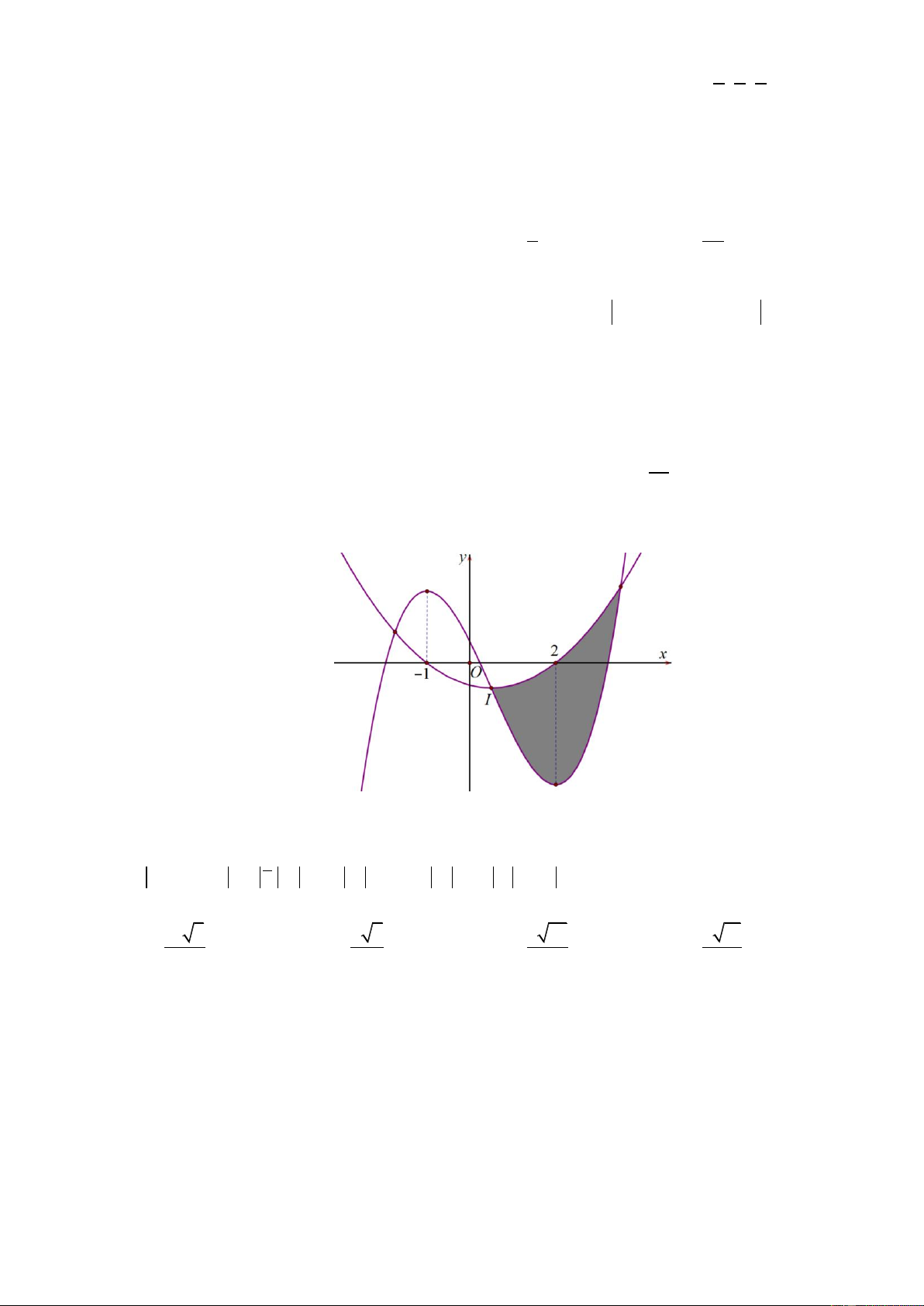
Câu 44. Một cái bình thủy tinh có phần không gian bên trong là một hình nón có đỉnh hướng xuống
dưới theo chiều thẳng đứng. Rót nước vào bình cho đến khi phần không gian trống trong bình
có chiều cao 2 cm. Sau đó đậy kín miệng bình bởi một cái nắp phẳng và lật ngược bình để đỉnh
hướng lên trên theo chiều thẳng đứng, khi đó mực nước cao cách đỉnh của nón 8 cm (hình vẽ minh họa bên dưới). 2 cm 8 cm
Biết chiều cao của nón là h a b cm. Tính T a b . A. 22 . B. 58 . C. 86 . D. 72 . Trang5  7 4 4 
Câu 45. Trong không gian với hệ trục tọa độ Oxyz cho điểm I 1;0;0 , điểm M ; ;   và đường  9 9 9  x  2 
thẳng d :  y t . N  , a ,
b c là điểm thuộc đường thẳng d sao cho diện tích tam giác IMN z 1t
nhỏ nhất. Khi đó a b c có giá trị bằng: 5 5 A. 2 . B. 2  . C. . D. . 2 2
Câu 46. Cho hàm số f x 4 3
x x  m   2 2
1 x  2x m  2022 , với m là tham số. Có bao nhiêu giá
trị nguyên của m thuộc đoạn  2
 021;2022 để hàm số y f x  202  1  2022 có số điểm
cực trị nhiều nhất? A.2021. B.2022. C.4040. D.2023
Câu 47. Có bao nhiêu số nguyên dương m để phương trình  x   x 2 1 .ln( 1)  2 x m e mx e e 1có 2
nghiệm phân biệt không lớn hơn 5. A.26. B.27. C.29. D.28. 7
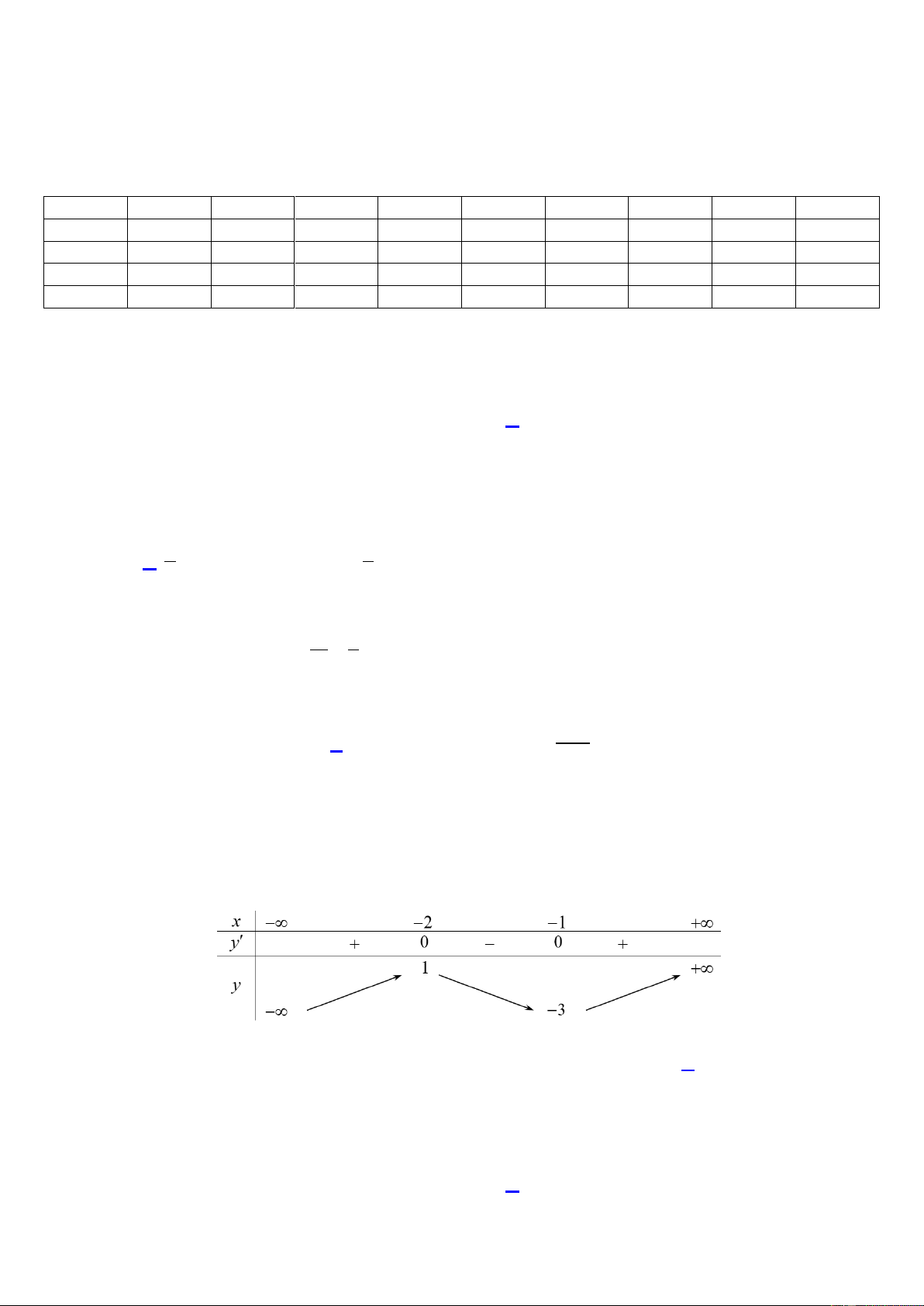
Câu 48. Cho hàm số f x với đồ thị là Parabol đỉnh I có tung độ bằng 
và hàm số bậc ba g x . 12
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thoả mãn 1 2 3 18x x x  5  5 (hình vẽ). 1 2 3
Diện tích miền tô đậm gần số nào nhất trong các số sau đây? A.5,7. B.5,9. C.6,1. D.6,3.
Câu 49. Cho M , N , P lần lượt là các điểm biểu diễn số phức z , z , z thỏa mãn điều kiện 1 2 3
5z  9  3i  5 z , z  2  z  3  i , z 1  z  3  4 . Khi M , N , P không thẳng hàng, 1 1 2 2 3 3
giá trị nhỏ nhất của nửa chu vi p của tam giác MNP là 10 5 6 5 9 10 5 11 A. . B. . C. . D. . 9 5 10 13
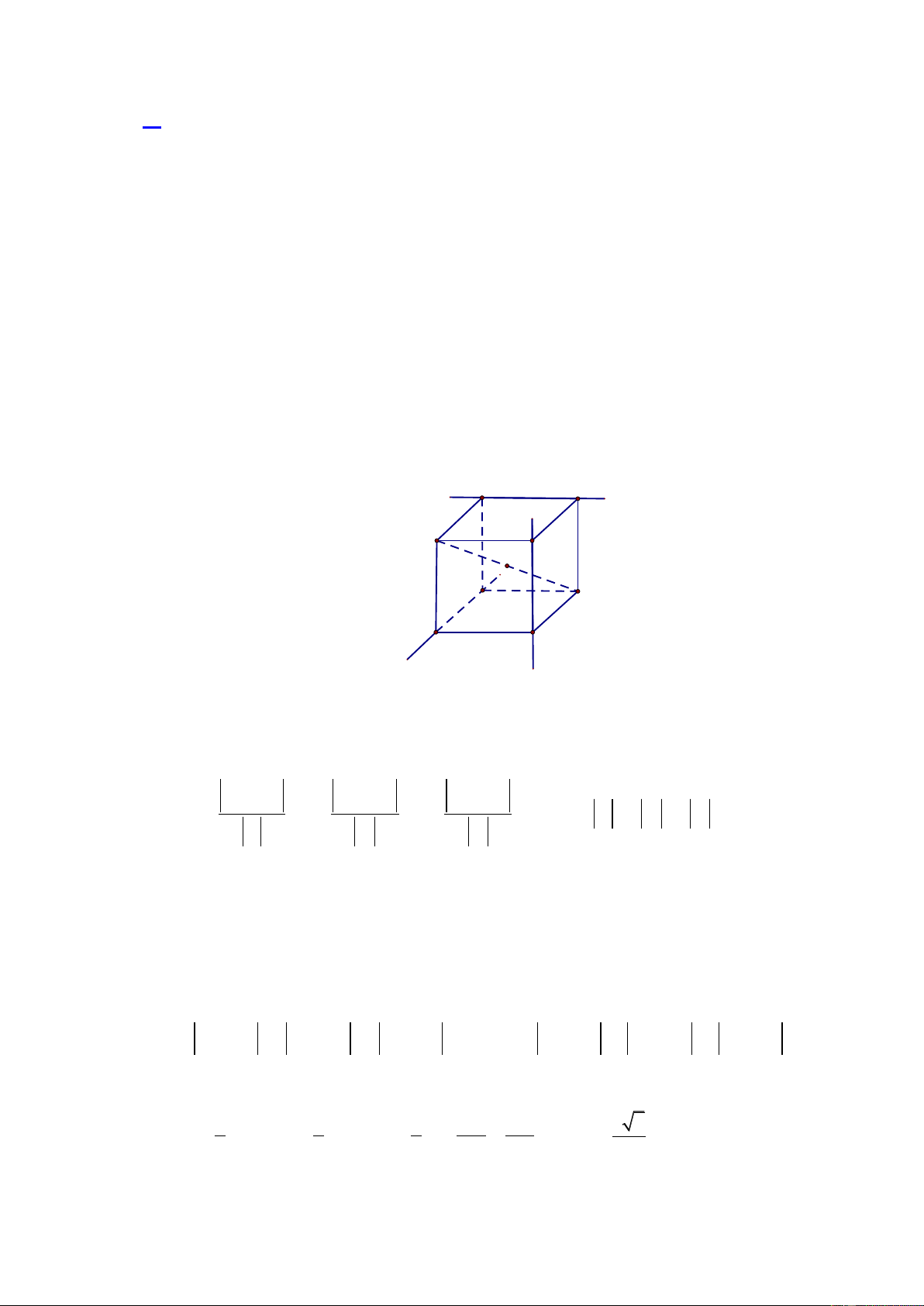
Câu 50. Trong không gian với hệ trục tọa độ Oxyz , cho 3 đường thẳng d , d , d có phương 3  2  1  x 1 2tx  3 t
x  4  2t 1  2  3 
trình d :  y  1 t , d :  y  1
  2t , d : y  4  2t . S I;R là mặt cầu tâm I bán 3  2  1  1  2  3  z  1 2tz  2  2t z  1 t 1  2  3
kính R tiếp xúc với 3 đường thẳng đó. Giá trị nhỏ nhất của R gần số nào nhất trong các số sau: A.2,1. B.2,2. C.2,3. D.2,4. Trang6 SỞ GD & ĐT THANH HÓA
KỲ THI KSCL CÁC MÔN THI TN THPT NĂM 2022 - LẦN 2
TRƯỜNG THPT CHUYÊN LAM SƠN Môn thi:Toán Ngày thi: 03/04/2022 ĐÁP ÁN ĐỀ GỐC BẢNG ĐÁP ÁN 1.C 2.A 3.B 4.D 5.C 6.D 7.C 8.A 9.A 10.A 11.D 12.B 13.D 14.C 15.A 16.C 17.D 18.D 19.C 20.D 21.B 22.A 23.A 24.B 25.C 26.C 27.C 28.A 29.A 30.A 31.A 32.C 33.A 34.C 35.D 36.C 37.C 38.C 39.C 40.D 41.B 42.C 43.C 44.C 45.B 46.A 47.D 48.A 49.B 50.A ĐÁP ÁN CHI TIẾT Câu 1.
Có bao nhiêu số tự nhiên có 4 chữ số khác nhau được lập từ tập A  2, 3, 4, 5,  6 A. 4 C . B. 4 C . C. 4 A . D. 4 A . 5 6 5 6 Lời giải
Số các số tự nhiên có 4 chữ số khác nhau được lập từ A là 4 A . 5 Câu 2.
Cho cấp số nhân u với u  8 và u  4 . Công bội của cấp số nhân đã cho bằng n  1 2 1 1 A. . B.  . C. 2  . D. 2 . 2 2 Lời giải u 1 Ta có 2
u u .q q   . 2 1 u 2 1 Câu 3.
Hàm số nào sau đây đồng biến trên  ? x 1 A. 3
y x  3x . B. 3
y x  3x . C. y
y x x  . x  . D. 4 2 3 1 1 Lời giải Nhận xét 3
y x  3x có 2
y  3x  3  0, x   . Do đó hàm số 3
y x  3x đồng biến trên  . Câu 4.
Cho hàm số y f x có bảng biến thiên như sau
Hàm số đạt cực đại tại điểm A. x  3  . B. x  1  .
C. x 1. D. x  2  . Lời giải
Qua bảng biến thiên ta có hàm số đạt cực đại tại điểm x  2  . Câu 5. Hàm số 4 2
y x x  3 có mấy điểm cực trị? A.1 . B. 2 . C. 3 . D. 0 . Lời giải Trang7 Hàm số 4 2
y x x  3 có ab  1.  1  1   0 , suy ra hàm số 4 2
y x x  3 có 3 điểm cực trị. 5x 1 Câu 6.
Đường thẳng nào sau đây là tiệm cận đứng của đồ thị hàm số y x ? 2
A. y  5 .
B. x  5.
C. x  2 . D. x  2  . Lời giải 5x  2 5x  2 Ta có: lim   lim   x   .   x 2  x  và 2 x 2  x  nên đồ thi có TCĐ: 2 2 Câu 7.
Trong các hàm số sau, hàm số nào có đồ thị như hình vẽ dưới đây? x 1 A. 3 2
y x x x 1 . B. y x . C. y y  log x . x  . D. 2 3 Lời giải ax b
Dễ nhận thấy dạng đồ thị cho trong bài là của hàm số dạng y cx  . d Câu 8.
Cho hàm số bậc ba y f x có đồ thị như hình vẽ dưới đây. Số nghiệm của phương trình
f x  1là: A.3. B.0. C.2. D.1. Lời giải
Kẻ đường thẳng y  1 ta thấy đường thẳng y  1 cắt đồ thị tại 3 điểm phân biệt. Như vậy số nghiệm của
phương trình f x 1là 3. Câu 9.
Tập xác định của hàm số y   x  35 1 là
A. 1;  .
B. 0;  . C.1;  . D.  \   1 . Lời giải
Điều kiện xác định: x 1 0  x 1.
Vậy tập xác định của hàm số là: D  1;  . Câu 10. Hàm số   4 2x f x   có đạo hàm là Trang8 xx
A. f  xx4  2 .ln 2.
B. f  xx4
 4.2 .ln 2. C. f  x 4 2  .
D. f  x 4 4.2  . ln 2 ln 2 Lời giải
Áp dụng công thức  u u aa .ln . a u .  
Ta có f  x   x4  x4  x   x4 2 2 .ln 2. 4  2 .ln 2 .
Câu 11. Tập nghiệm của phương trình log  x  
1  log 2x  3  0 là  2  A.  4;   . B.  2  . C.  4  . D.  . 3  Lời giải x 1  2x  3 x  4 
Ta có phương trình đã cho     x 1 x 1
Phương trình trên vô nghiệm. 1
Câu 12. Trên khoảng ;  2 , họ nguyên hàm của hàm số f (x)  x  là 2 1 1  1 A.C x   C . C.C . D.
ln x  2  C . x  . B. ln 2 2 x  22 2 Lời giải 1 1 1 Áp dụng công thức: dx
ln ax b C  , ta có
dx  ln x  2  C  . ax b a x  2
Câu 13. Trong các mệnh đề sau, mệnh đề nào sai? A. f
 xdx f xC . B. cos d
x x  sin x C  .  1   x
C. x dx   C,    1  x x       . D. a dx a ln a C  0 a  1 . 1 Lời giải x a Ta có x a dx   C  0  a   1 nên phương án xd x
a x a ln a C  0  a   1 sai. ln a 1 Câu 14. Tích phân 3 e xdx  bằng 0 1 3 e 1 A. 3 e  . B. e 1. C. . D. 3 e 1 . 2 3 Lời giải 1 1 1 3  x 1 x 1 x e 1 Ta có 3 3 e dx  e d 3x 3  e    . 3 3 3 0 0 0 1 2022
Câu 15. Xét I  2x
  2x 2 dx, nếu đặt 2
u x  2 thì I bằng 0 3 1 3 3 1 A. 2022 u du  . B. 2022 u du  . C. 2022 2 u du  . D. 2022 u du  . 2 2 0 2 2 Lời giải Trang9 1 1 20202 2022 Xét I  2x
  2x 2 dx   2x 2 d  2x 2 0 0 3 Đặt 2
u x  2 . Đổi cận: x  0  u  2 ; x 1 u  3 .Khi đó 2022 I u du  2
Câu 16. Cho số phức z  3 2i . Tìm phần ảo của số phức liên hợp của z . A. 2  . B. 2i . C. 2 . D. 2  i . Lời giải
Số phức liên hợp của z là z  3  2i .
Vậy phần ảo của số phức liên hợp của z là 2 .
Câu 17. Cho hai số phức z  1 2i , z  2  6i . Tích z .z bằng 1 2 1 2 A. 1  0 2i .
B. 2 12i . C.14 10i . D.14  2i . Lời giải
Ta có z .z  1 2i
2  6i  14  2i . 1 2   
Câu 18. Xét hai số phức z , z tùy ý. Phát biểu nào sau đây sai? 1 2
A. z z z .z .
B. z z z . z .
C. z z z z .
D. z z z z . 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 Lời giải
Giả sử z a bi , z c di  , a , b ,
c d    , ta có 1 2
z z  a c2  b d 2 mà 2 2 2 2 z z
a b c d 1 2 1 2
Vậy về tổng quát z z z z . 1 2 1 2
Câu 19. Một khối lăng trụ có thể tích bằng V , diện tích mặt đáy bằng S . Chiều cao của khối lăng trụ đó bằng S 3V V S A. . B. . C. . D. . V S S 3V Lời giải
Gọi h là chiều cao của khối lăng trụ. V
Ta có thể tích khối lăng trụ là V S.h h  . S
Câu 20. Cho khối chóp S.ABC có đáy là tam giác đều cạnh a , SA   ABC  , SA a (tham khảo hình vẽ bên dưới).
Thể tích của khối chóp đã cho bằng: 3 3a 3 3a 3 3a A. . B. . C. 3 3a . D. . 4 6 12 Trang10 Lời giải
Vì SA   ABC  nên ta có SA là đường cao của hình chóp hay h SA a . 2
Do đáy của hình chóp là tam giác đề a 3
u cạnh a nên ta có: S  . 4 2 3 Khi đó thể 1 3a 3a
tích của khối chóp đã cho là: 1 V S.h  . .a  (đvtt). 3 3 4 12
Câu 21. Cho hình nón có bán kính đáy R  3 và độ dài đường sinh l  4 . Tính diện tích xung quanh
S của hình nón đã cho. xq A. S 12 . B. S  4 3 . C. S  39 . D. S  8 3 . xq xq xq xq Lời giải
Ta có S   Rl . Nên S   3.4  4 3 . xq xq
Câu 22. Tính thể tích của khối trụ biết bán kính đáy của khối trụ đó bằng a và chiều cao bằng 2a A. 3 2 a . B. 3  a . C. 3 4 a . D. 2 2 a . Lời giải Thể tích khối trụ là 2 2 3
V   r h   a .2a  2 a .
Câu 23. Trong không gian với hệ trục tọa độ Oxyz , hình chiếu vuông góc của điểm A1; 2;3 trên mặt phẳng Oyz là
A. M 0; 2;3 .
B. N 1;0;3 .
C. P 1;0;0 .
D. Q 0; 2;0 . Lời giải
Hình chiếu của điểm M  ;
x y; z  lên mặt phẳng Oyz là M 0; ; y z
Nên M 0; 2;3 là hình chiếu của điểm A1;2;3 trên mặt phẳng Oyz .
Câu 24. Trong không gian với hệ trục tọa độ Oxyz , cho điểm (
A 1 ; 2 ; 3) và mặt phẳng
(P) : 3x  4 y  7z  2  0 . Đường thẳng đi qua A và vuông góc với mặt phẳng (P) có phương trình là x  3 tx 1 3t   A. y  4
  2t (t  ).
B. y  2  4t (t   ).   z  7  3tz  3  7t  x 1 3tx 1 4t  
C. y  2  4t (t   ).
D. y  2  3t (t   ).   z  3  7tz  3  7tLời giải Trang11
Gọi u là véc tơ chỉ phương của đường thẳng () thỏa mãn yêu cầu bài toán. 
Ta có véc tơ pháp tuyến của mặt phẳng (P) : n   p (3; 4;7) .   x 1 3t (  )  (P) u
   n    p (3; 4;7) Vì   
 () : y  2  4t (t  ). A()  ( A 1; 2;3)  () z  37t
Câu 25. Trong không gian với hệ trục tọa độ Oxyz , mặt cầu tâm I 1;0;0 và bán kính bằng 2 có phương trình là
A. x  2 2 2
1  y z  2 .
B. x  2 2 2
1  y z  2 .
C. x  2 2 2
1  y z  4 .
D. x  2 2 2
1  y z  4 . Lời giải
Phương trình mặt cầu có tâm I  ; a ;
b c và bán kính R có dạng:
  2   2   2 2 x a y b z cR
Mà tâm I 1;0;0 và bán kính R  2 nên  x  2 2 2
1  y z  4.
Câu 26. Một em bé có bộ 7 thẻ chữ, trên mỗi thẻ có ghi một chữ cái, trong đó có 2 thẻ chữ T giống
nhau, một thẻ chữ H, một thẻ chữ P, một thẻ chữ C, một thẻ chữ L và một thẻ chữ S. Em bé xếp
theo hàng ngang ngẫu nhiên 7 thẻ đó. Xác suất em bé xếp được dãy theo thứ tự THPTCLS là 1 1 2 1 A. . B. . D. . 7 2  . C. 6! 7! 7! Lời giải
Hoán vị 7 chữ cái này ta được 1 dãy 7 chữ cái, tuy nhiên trong đó có 2 chữ T giống nhau nên
khi hoán vị 2 chữ T này cho nhau không tạo dãy mới. 7! Vì vậy sẽ có:   dãy khác nhau. 2! 1 2
Xác suất để tạo thành dãy THPTCLS là P   . 7! 7! 2!
Câu 27. Cho hình chóp S.ABC có đáy là tam giác vuông tại B , AB  3a , BC  3a ; SA vuông góc
với mặt phẳng đáy và SA  2a .Góc giữa đường thẳng SC và mặt phẳng đáy  ABC  bằng A. ο 60 . B. ο 45 . C. ο 30 . D. ο 90 . Lời giải
Ta có SA   ABC  nên góc giữa SC và  ABC  bằng  ACS . 2 2 2 2 AC
AB BC  9a  3a  2a 3 . Trang12 SA a Suy ra  2 1 tan ACS     ο  ACS  30 . AC 2a 3 3
Câu 28. Cho hàm số bậc bốn y f x . Hàm số y f  x có đồ thị như hình vẽ sau
Hàm số y f x nghịch biến trên khoảng nào trong các khoảng sau? A. 1; 4 . B. 1;  1 . C. 0;3 . D. ;0 . Lời giải
Dựa vào đồ thị hàm số y f  x ta có
f  x  0  x  1  ; 
1  4;   và f  x  0  x ;  1  1; 4 .
Do đó hàm số y f x đồng biến trên các khoảng 1; 
1 và 4;   , nghịch biến trên các khoảng ;  1 và 1; 4 .
Vậy hàm số y f x nghịch biến trên khoảng 1; 4 là đúng.
Câu 29. Khi nuôi tôm trong một hồ tự nhiên, một nhà khoa học đã thống kê được rằng: nếu trên mỗi
mét vuông mặt hồ thả x con tôm giống thì cuối vụ mỗi con tôm có cân nặng trung bình là 2
108  x (gam). Hỏi nên thả bao nhiêu con tôm giống trên mỗi mét vuông mặt hồ tự nhiên đó để
cuối vụ thu hoạch được nhiều tôm nhất. A.6. B.7. C.8. D.9. Lời giải
Sau một vụ lượng tôm trung bình trên mỗi 2
m mặt hồ nặng x  2  x  3 108
108x x (ga ) m Xét hàm số 3
f (x)  108x x trên khoảng (0; ) ta có x  6 2 2
f '(x)  108  3x ; f '(x)  0  108  3x  0   x  6   0
Trên khoảng (0; ) hàm số 3
f (x)  108x x đạt GTLN tại x  6 .
Vậy nên thả 6 con tôm giống trên mỗi mét vuông mặt hồ thì cuối vụ thu hoạch được nhiều tôm nhất.
Câu 30. Xét tất cả các số dương a và b thỏa mãn log a  log b  log
ab . Tính giá trị của ab . 3 3 9   1
A. ab 1.
B. ab  2 . C. ab  .
D. ab  0 . 2 Lời giải Trang13 1
Ta có: log a  log b  log ab  log ab  log ab  log ab  log ab 2 3 3 9 3   3   3   3 2 1
 log ab  0  ab  1. 3   2
Câu 31. Tích tất cả các nghiệm của phương trình 2 2 x 5x4 2  4 bằng A.1 . B. 2  . C. 2 . D. 1. Lời giải  1   2 2 x
Ta có: 2x 5x4 2 x 5 x4 2 2 2 2 4 2 2 2x 5x 4 2 2x 5x 2 0              2  . x  2 
Vậy tích các nghiệm của phương trình là 1 . 2 3x  1 
Câu 32. Số nghiệm nguyên của bất phương trình 5 x2  5   là  5  A. 3 . B.1 . C. 2 . D. 4 . Lời giải 2 3  x 2  1  Bất phương trình 5 x2 3x 5 x2 2  5  5  5
 3x  5x  2    5  1 2
 3x  5x  2  0    x  2 . 3
Vì x  nên x 0 
;1 . Vậy bất phương trình có 2 nghiệm nguyên. 1
Câu 33. Cho hàm số f x liên tục trên đoạn 0; 
1 ,có đạo hàm f  x thỏa mãn 2x  
1 f  xdx  10 0 1
và f 0  3 f   1 . Tính I f
 xdx . 0 A. I  5  .
B. I  2 .
C. I  2 . D. I  5 . Lời giải
Đặt: u  2x 1 du  2dx , dv f xdx chọn v f x . 1 1 1
Ta có: 2x  
1 f  x dx  10  2x  
1 f x  2 f
 xdx 10 0 0 0 1 1 1  3 f  
1  f 0  2 f
 xdx 10  02 f
 xdx 10  f xdx  5   . 0 0 0
Câu 34. Tìm số phức z thỏa mãn z  2z  9  2i .
A. z  3 2i .
B. z  3 i .
C. z  3 2i .
D. z  2  3i . Lời giải
Đặt z a bi  , a b R .
Theo giả thiết ta có a bi  2a bi  9  2i .
Điều này tương đương với 3a 9  b  2i  0 .
Từ đây ta được 3a  9  b  2  0 .
Như vậy a  3 và b  2  .
Tức là z  3 2i . Trang14 x  2 y z 1
Câu 35. Trong không gian với hệ trục tọa độ Oxyz , cho đường thẳng  :    . Gọi M là 3 1 2
giao điểm của  với mặt phẳng P : x  2y 3z  2  0. Tọa độ điểm M là
A. M 2;0;   1 .
B. M 5; 1; 3 . C. M 1;0  ;1 . D. M  1  ;1  ;1 . Lời giải x  2 y   3  1 
x  3y  2 x  1   y z 1  
Tọa độ của điểm M là nghiệm của hệ:  
 2y z 1  y 1 1 2    
x  2 y  3z  2  z  1
x  2 y  3z  2  0    Vậy M  1  ;1;1.
Câu 36. Trong không gian với hệ trục tọa độ Oxyz ,  P là mặt phẳng đi qua điểm M 1; 2;3 và cắt các
tia Ox, Oy, Oz lần lượt tại ,
A B, C (khác gốc tọa độ O ) sao cho M là trực tâm tam giác ABC .
Biết mặt phẳng  P có phương trình ax by cz 14  0 . Tính tổng T a b c . A.8. B.14. C.6. D.11. Lời giải
Ta có tứ diện OABC là tứ diện vuông tại O , mà M là trực tâm tam giác ABC nên
OM   ABC   OM  P . 
Vậy OM 1;2;3 là một véc tơ pháp tuyến của mặt phẳng  P và  P đi qua M nên  P có
phương trình: x  2y  3z 14  0  T a b c  6 .
Câu 37. Trong không gian với hệ trục tọa độ Oxyz , cho điểm A7; 1; 2 và mặt phẳng
P: x 2y  2z 6  0 . Mă ̣t cầu S tâm A và tiếp xúc với mặt phẳng P có phương trình là 2 2 2 49 2 2 2 7
A. x  7   y  
1   z  2  .
B. x  7   y  
1   z  2  . 9 3 2 2 2 49 2 2 2 7
C. x  7   y  
1   z  2  .
D. x  7   y  
1   z  2  . 9 3 Lời giải
Mă ̣t cầu S  tâm A và tiếp xúc với mặt phẳng P có bán kính là    
R d A P 7 2.  1 2.2 6 7 ,   .   2 2 2 3 1 2  2 Vâ ̣y mă ̣t cầu  2 2 2 49
S  có phương trình là  x  7   y  
1   z  2  . 9
Câu 38. Cho hình lăng trụ đứng AB .
C A' B 'C ' có đáy ABC là tam giác đều cạnh a . Cạnh BA'  a 3 .
Khoảng cách giữa hai đường thẳng A ' B và B 'C là: a a 2 2a A. a 2 . B. . C. . D. . 3 3 3 Lời giải. Trang15 A' C' B' H E M A C B AA'  a 2
Gọi M là trung điểm AC , E AB' A' B E là trung điểm của AB '
Khi đó B 'C / /ME B 'C / /  A'BM
d B'C, A'B  d B'C, A'BM   d C, A'BM   d  ,
A A' BM  (*)
Trong mặt phẳng  A' AM  :kẻ AH A' M (1) Do ABC
đều  BM AC AB .
C A' B 'C ' là hình lăng trụ đứng  AA'   ABC   AA'  BM
Nên BM   A' AM   BM AH (2)
Từ (1) và (2)  AH   A' BM   d  ,
A A' BM   AH (**)
Trong tam giác A ' AM vuông tại A , AH là đường cao: 1 1 1 1 4 9 a 2       AH  (***) 2 2 2 2 2 2 AH A' A AM 2a a 2a 3 a
Từ (*), (**), (***)  d A B B C 2 ' , '  . 3
Câu 39. Gọi S là tập hợp tất cả các giá trị thực của tham số m để đồ thị C của hàm số 4 2 2 4
y x  2m x m  5 có ba điểm cực trị, đồng thời ba điểm cực trị đó cùng với gốc tọa độ O
tạo thành một tứ giác nội tiếp. Tìm tích các phần tử của S . 1 1 A. 2 . B. . C. . D. 2  . 5 5 Lời giải Để hàm số 4 2 2 4
y x  2m x m  5 có ba điểm cực trị thì y '  0 phải có ba nghiệm phân biệt.  x  0  Ta có 3 2
y x m x x 2 2 ' 4 4 4
x m  . y '  0  x m , m  0 .  x  m
Ba điểm cực trị là A 4
0;m  5, B ;
m 5,C  ; m 5 . Trang16 Ba điểm ,
A B,C và gốc tọa độ O 0;0 tạo thành tứ giác nội tiếp khi và chỉ khi   B C         1 B C  , (do  
B C )  B . A BO  0 2 4
m  5m  0 2
m  . Vậy S có 2 phần tử và 2 5 1 có tích bằng . 5
Câu 40. Gọi S là tập nghiệm của bất phương trình
 2x x    2 log 2 log
x  2x  3 . Biết S  m;na a  7 và
thuộc S , tính m n . 3 13 7 11 9
A. m n  .
B. m n  .
C. m n  .
D. m n  . 3 2 3 2 Lời giải 2
x x  2  0  2  x  3 Điều kiện: 2
x  2x  3  0   .  0  a  1 0  a  1  7 Do x
là nghiệm của bất phương trình đã cho nên 10 20 log  log  0  a  1. 3 a 9 a 9
Vì 0  a 1 nên bất phương trình 2 2
x x  2  x  2x  3 5  5 9 x 5 2 2 3
 2x  3x  5  0  1
  x   2  x  . Vì vậy m n  2   2 2 2 2   
Câu 41. Cho hàm số y f x liên tục trên đoạn 0;   thỏa mãn:  2     2cos .
x f 1 4sin x  sin 2 .
x f 3  2cos 2x  sin 4x  4sin 2x  4cos x , x   0;   .  2  5 Khi đó I f
 xdxbằng 1 A.2. B.0. C. 8 . D.16 . Lời giải Ta có: 2 cos .
x f 1 4sin x  sin 2 .
x f 3  2cos 2x  sin 4x  4sin 2x  4cos x (*) 
Lấy tích phân từ 0 đến
hai vế của (*) ta được: 2    2 2 cos . x f  1 4sin x 2 dx  sin 2 . x f  32cos2x 2
dx  sin 4x  4sin 2x 4cos xdx 0 0 0 Trang17   2 1  f    x 2 1 1 4sin
d (1 4sin x)  f
 32cos2xd(32cos2x)  0 2 4 0 0 5 5 5 5 1  f  t 1 dt f
 tdt  0  f
 tdt  0  f
 xdx  0 2 4 1 1 1 1 5 Vậy I f
 xdx = 0. 1
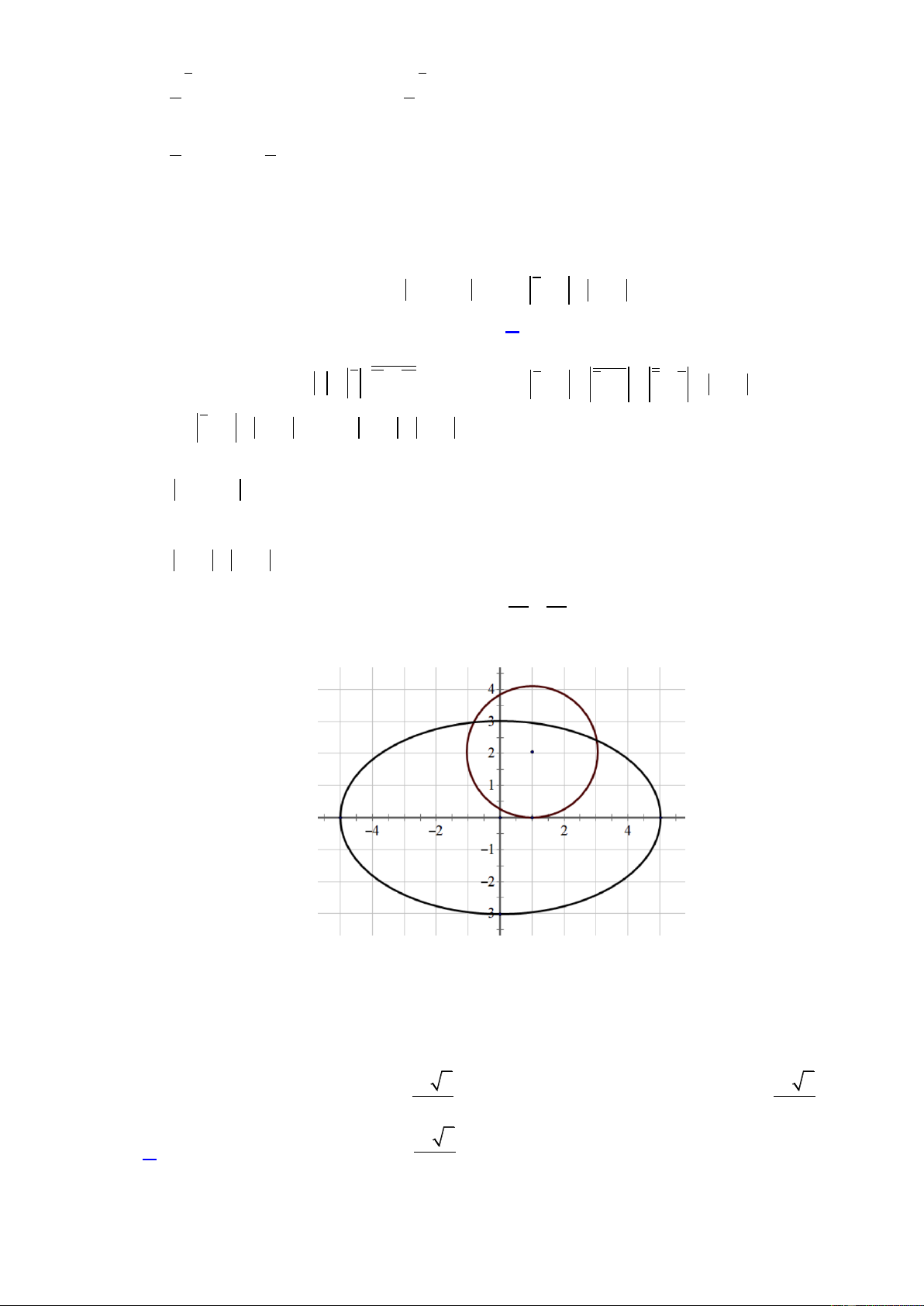
Câu 42. Có bao nhiêu số phức z thỏa mãn z 1 2i  2 và z  4  z  4  10 ? A.1 . B. 0 . C. 2 . D. 4 . Lời giải
Áp dụng các tính chất z z ; z z z z ta có z  4  z  4  z  4  z  4 . 1 2 1 2
Do đó z  4  z  4 10  z  4  z  4 10 .
Gọi M là điểm biểu diễn của z .
Do z 1 2i  2 nên M thuộc đường tròn C tâm I 1; 2 , bán kính R  2 . C có phương 2 2
trình là  x  
1   y  2  4 .
Do z  4  z  4  10 nên M thuộc đường elip  E có hai tiêu điểm là F 4  ;0 ; F 4;0 và 2   1   2 2 có độ x y
dài trục lớn là 10 .  E có phương trình là  1. 25 9
Từ đây có M là giao điểm của C và  E .
Từ hình vẽ của C và  E ta thấy chúng có 2 giao điểm nên có 2 số phức thỏa mãn yêu cầu.
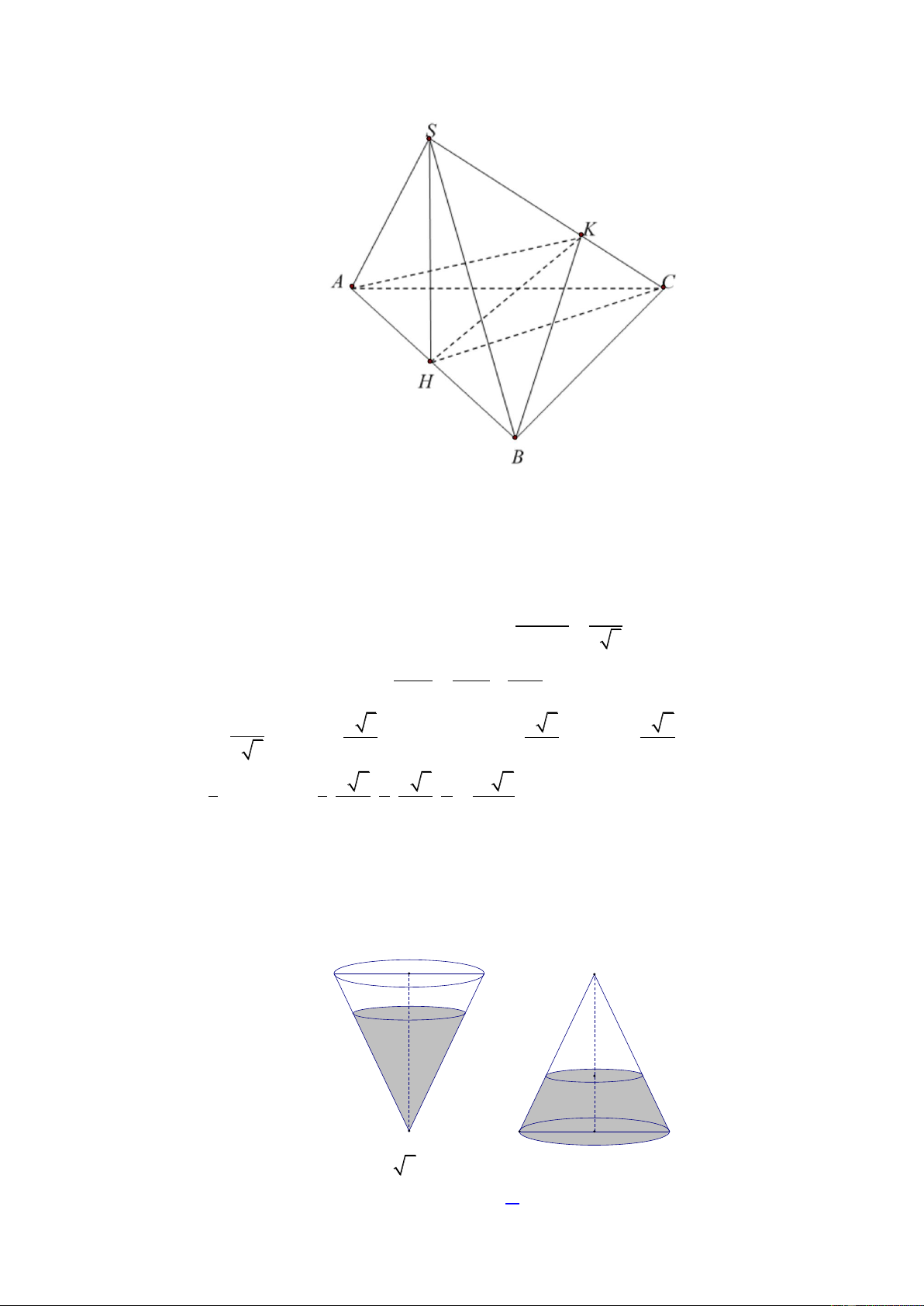
Câu 43. Cho hình chóp S.ABC có đáy là tam giác đều cạnh bằng a , tam giác SAB cân tại S và thuộc
mặt phẳng vuông góc với mặt phẳng  ABC  , góc giữa hai mặt phẳng SCA và SCB bằng 0
60 . Gọi H là trung điểm của đoạn AB . Trong các mệnh đề sau, mệnh đề nào đúng: 3 a 2 3 a 2
A.Thể tích khối chóp S.ABC bằng .
B.Thể tích khối chóp . B SHC bằng . 16 16 3 a 2
C.Thể tích khối chóp S.AHC bằng .
D.Không tồn tại hình chóp đã cho. 64 Lời giải Trang18
Tam giác SAB thuộc mặt phẳng vuông góc với mặt phẳng  ABC   SH   ABC , từ đó suy
ra đường cao của hình chóp S.AHC là SH
Kẻ AK SC SC   AKB  SC KB  0    AKB 60
SAC  SBC   KA KB 0 ; ;  60    0 AKB 120 Nếu  0
AKB  60 thì dễ thấy KAB đều  KA KB AB AC (vô lí). Vậy  0 AKB  120 khi đó  AH a
KAB cân tại K và  0
AKH  60  KH   0 tan 60 2 3 1 1 1 Trong S
HC vuông tại H ta có   2 2 2 KH HC HS a a 3 a 6 a 6 thay KH  và HC
vào ta được SH  . Vậy h  . 2 3 2 8 8 3 1
1 a 6 1 a 3 a a 2 V  .SH.dt  . . . .  . S.AHC  3 AHC 3 8 2 2 2 64
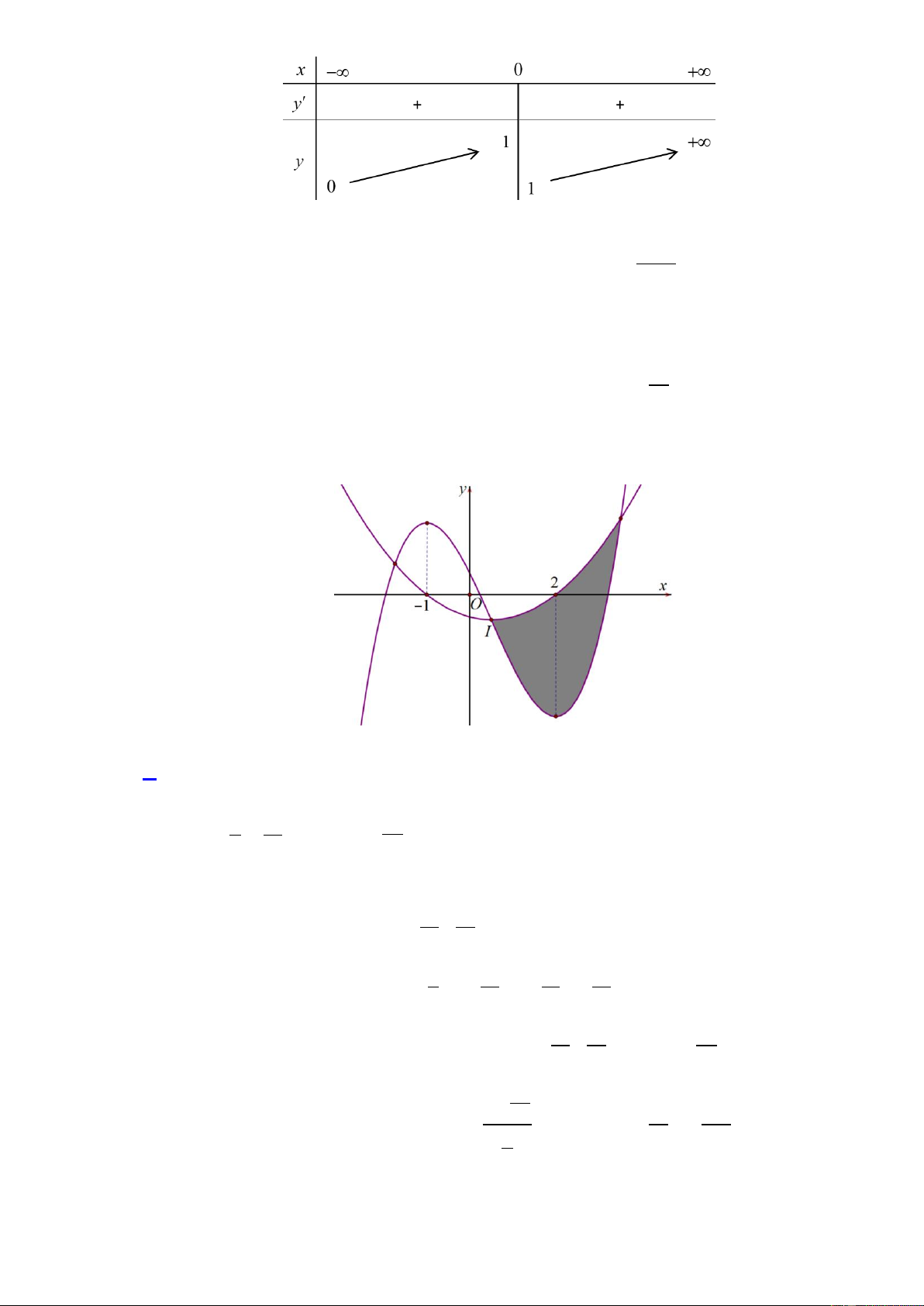
Câu 44. Một cái bình thủy tinh có phần không gian bên trong là một hình nón có đỉnh hướng xuống
dưới theo chiều thẳng đứng. Rót nước vào bình cho đến khi phần không gian trống trong bình
có chiều cao 2 cm. Sau đó đậy kín miệng bình bởi một cái nắp phẳng và lật ngược bình để đỉnh
hướng lên trên theo chiều thẳng đứng, khi đó mực nước cao cách đỉnh của nón 8 cm (hình vẽ minh họa bên dưới). 2 cm 8 cm
Biết chiều cao của nón là h a b cm. Tính T a b . A. 22 . B. 58 . C. 86 . D. 72 . Lời giải Trang19
Để ý rằng có 3 hình nón đồng dạng: Phần không gian bên trongbình thủy tinh (có thể tích V ),
phần không chứa nước khi đặt bình có đỉnh hướng lên (có thể tích V ), phần chứa nước khi đặt 1
bình có đỉnh hướng xuống (có thể tích V ). Do tỷ số đồng dạng bằng với tỷ số của chiều cao và 2
tỷ số thể tích là lập phương tỷ số đồng dạng nên ta có V h V h 512Vh  23 3 3 V  ;  V  ; V
. Mà V V V nên ta có: 3 1 2 V 8 Vh  23 1 3 2 3 h h 1 2 512Vh23V 3 2 3 2 
V  512  h  6h 12h 8  h h  2h 84  0  h 1 85 3 3 h h Vậy T  86  7 4 4 
Câu 45. Trong không gian với hệ trục tọa độ Oxyz cho điểm I 1;0;0 , điểm M ; ;   và đường  9 9 9  x  2 
thẳng d :  y t . N  , a ,
b c là điểm thuộc đường thẳng d sao cho diện tích tam giác IMNz 1t
nhỏ nhất. Khi đó a b c có giá trị bằng: 5 5 A. 2 . B. 2  . C. . D. . 2 2 Lời giải 2 Ta có IM  . 3 1 1
Gọi H là hình chiếu của N trên đường thẳng d ' đi qua I , M , ta có: S
IM .NH NH IMN  2 3
Diện tích tam giác IMN nhỏ nhất khi và chỉ khi độ dài NH nhỏ nhất. 
N d N 2; ;
n 1 n  IN  1; ; n 1 n .   
Đường thẳng d 'có vecto chỉ phương u '  1; 2  ; 2
  . IN,u '  2;n 3;n  2   . 2    5  9   2 2 2 n   2           
NH d N d IN ,u ' 2
n 3  n 2 2 4 1 ; '      . u ' 3 3 2 5  5 3 
Dấu  xảy ra khi n  
, suy ra: N 2;  ;  
 .Vậy a b c  2  . 2  2 2 
Câu 46. Cho hàm số f x 4 3
x x  m   2 2
1 x  2x m  2022 , với m là tham số. Có bao nhiêu giá
trị nguyên của m thuộc đoạn  2
 021;2022 để hàm số y f x  202  1  2022 có số điểm
cực trị nhiều nhất? A.2021. B.2022. C.4040. D.2023 Lời giải
Hàm số y f x  202 
1  2022 có số điểm cực trị nhiều nhất là 7 khi và chỉ khi phương
trình f x  202 
1  2022 có 4 nghiệm phân biệt hay phương trình f x  2022 có 4 nghiệm phân biệt
Ta có f x 4 3
 2022  x x  m   2 2
1 x  2x m  0 Trang20x  1     x   1  x   2
1 x  2x m  0  x  1     2
x  2x m  0  *
Suy ra f x  2022 có 4 nghiệm phân biệt khi và chỉ khi * có 2 nghiệm phân biệt khác 1 và 1tức là 1   m  0  m 1 2 1
  2  m  0  
do m nguyên thuộc  2
 021;2022 nên có 2021 giá trị thỏa mãn.  m  3  2 1  2 m  0  
Câu 47. Có bao nhiêu số nguyên dương m để phương trình  x   x 2 1 .ln( 1)  2 x m e mx e e 1có 2
nghiệm phân biệt không lớn hơn 5. A.26. B.27. C.29. D.28. Lời giải
Xét phương trình  x   x 2 1 .ln( 1)  2 x m e mx e e
1 (*) điều kiện mx 1 0 x   e 1 0 *   xe 1  . m ln(mx 1) x
e 1  0  x  0 x e 1  .
m ln(mx 1) , Đặt  ln( 1) x y mx
e 1  m . y
x  ln(my 1)(1)
Ta có hệ phương trình 
y  ln(mx 1)(2)
Trừ (1) và (2) theo vế ta được: x y  ln(my 1)  ln(mx 1) hay x  ln(mx 1)  y  ln(my 1) với m  0 thì hàm số
f (x)  x  ln(mx 1) đồng biến trên tập xác định nên
x  ln(mx 1)  y  ln(my 1)  x y
Thay x y vào (1) ta được x  ln(mx 1) hay x
e mx 1(4)
Rõ ràng x  0 là 1 nghiệm của phương trình (4). x e 1
Với x  0 ta có (4)  m x x e 1 x x xe e 1
Xét hàm số g(x) 
, ta có: Tập xác định D   \ {0} và g (  x)  x 2 x (  )  0 x x g x
xe e 1  0 Hàm số ( ) x x
h x xe e 1 có (  ) x
h x xe nên h (
x)  0  x  0
Ta có bảng biến thiên của h(x) như sau:
Suy ra h(x)  0 , x
 do đó g (x)  0 , x   0
Bảng biến thiên của g(x) : Trang21
Để phương trình x 1  ln( 1)m e mx
có 2 nghiệm phân biệt không lớn hơn 5 thì phương trình 5 e 1
m g(x) có duy nhất 1 nghiệm bé hơn hoặc bằng 5. Ta có g(5)   29,5 5 0
  m g(5)
Dựa vào bảng biến thiên của g(x) ta có  do *
m   nên có 28 giá trị thỏa mãn. m 1 7
Câu 48. Cho hàm số f x với đồ thị là Parabol đỉnh I có tung độ bằng 
và hàm số bậc ba g x . 12
Đồ thị hai hàm số đó cắt nhau tại ba điểm phân biệt có hoành độ x , x , x thoả mãn 1 2 3 18x x x  5  5 (hình vẽ). 1 2 3
Diện tích miền tô đậm gần số nào nhất trong các số sau đây? A.5,7. B.5,9. C.6,1. D.6,3. Lời giải  1 7  7 Dễ thấy I ,  
 và f x  x   1  x  2 .  2 12  27
Hàm số g x đạt cực trị tại x  1, x  2 nên   
x  a x   x    g x 3 2 x x g ' 1 2
a    2x  b  3 2    Đồ 1 7 7 13
thị hàm số g x đi qua I nên g       a  , b    1 .  2  12 12 12 3 2   Phương trình hoành độ x x 7
giao điểm: f x  g x  a  
 2x   b  x   1  x  2  3 2  27 14 b  Theo đị 28 55a nh lý viet ta có: 27 18x x x  55   18.  55  18b    , 2 1 2 3 a 3 3 3 Trang22 x x Từ  
1 , 2 ta được a b   g x 3 2 1 1 1,  
 2x  . Từ đó suy ra diện tích miền tô 2 3 2 2 đậm sấp sỉ 5,7.
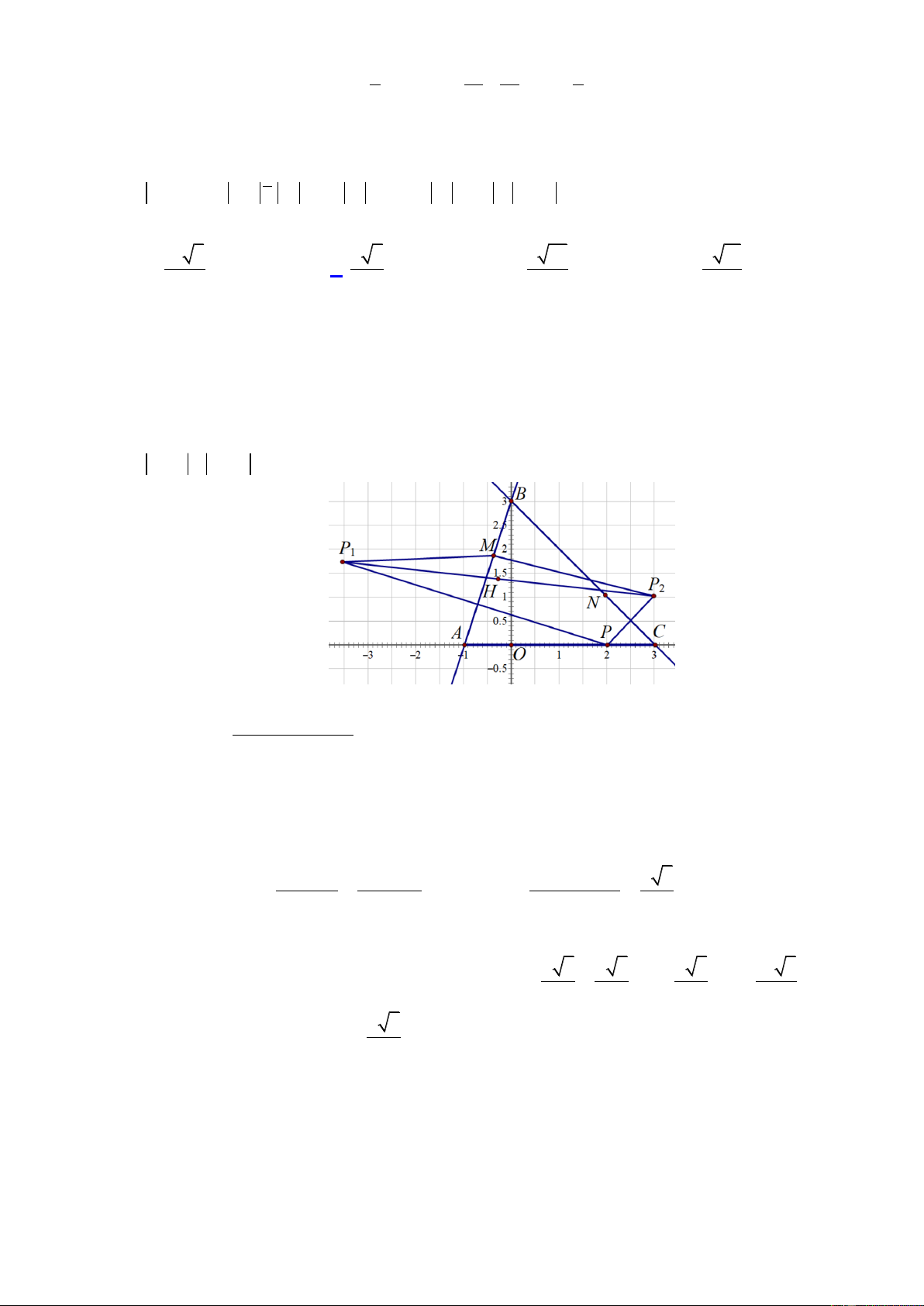
Câu 49. Cho M , N , P lần lượt là các điểm biểu diễn số phức z , z , z thỏa mãn điều kiện 1 2 3
5z  9  3i  5 z , z  2  z  3  i , z 1  z  3  4 . Khi M , N , P không thẳng hàng, 1 1 2 2 3 3
giá trị nhỏ nhất của nửa chu vi p của tam giác MNP là 10 5 6 5 9 10 5 11 A. . B. . C. . D. . 9 5 10 13 Lời giải
Trong mặt phẳng Oxy , gọi A 1
 ;0 , B0;3, C 3;0 và M , N, P lần lượt là các điểm biểu
diễn số phức z , z , z . Ta có 1 2 3
Tập hợp điểm M biểu diễn số phức z là đường thẳng AB . 1
Tập hợp điểm N biểu diễn số phức z là đường thẳng BC . 2
z 1  z  3  4  PAPC AC  Tập hợp điểm P biểu diễn số phức z là đoạn AC . 3 3 3   Khi đó MN NP PM p  . 2
Gọi P , P lần lượt đối xứng với P qua AB , BC . Ta có MP MP , NP NP . 1 2 1 2
Khi đó MN NP PM PM MN NP PP . 1 2 1 2 Ta thấy        
P BP P BA ABC CBP PBA ABC PBC  2ABC . 1 2 1 2  Theo đị AB AC AC sin BCA 2 5 nh lí Sin:        sin ABC sin BCA sin ABC AB 5
Gọi H là trung điểm của P P , khi đó 1 2   2 5 4 5 4 5 12 5
PP  2P H  2BP .sin P BH  2B .
P sin ABC  2B . PBP BO  . 1 2 2 2 2 5 5 5 5 6 5
Vậy giá trị nhỏ nhất của p là . 5
Câu 50. Trong không gian với hệ trục tọa độ Oxyz , cho 3 đường thẳng d , d , d có phương 3  2  1  x 1 2tx  3 t
x  4  2t 1  2  3 
trình d :  y  1 t , d :  y  1
  2t , d : y  4  2t . S I;R là mặt cầu tâm I bán 3  2  1  1  2  3  z  1 2tz  2  2t z  1 t 1  2  3 Trang23
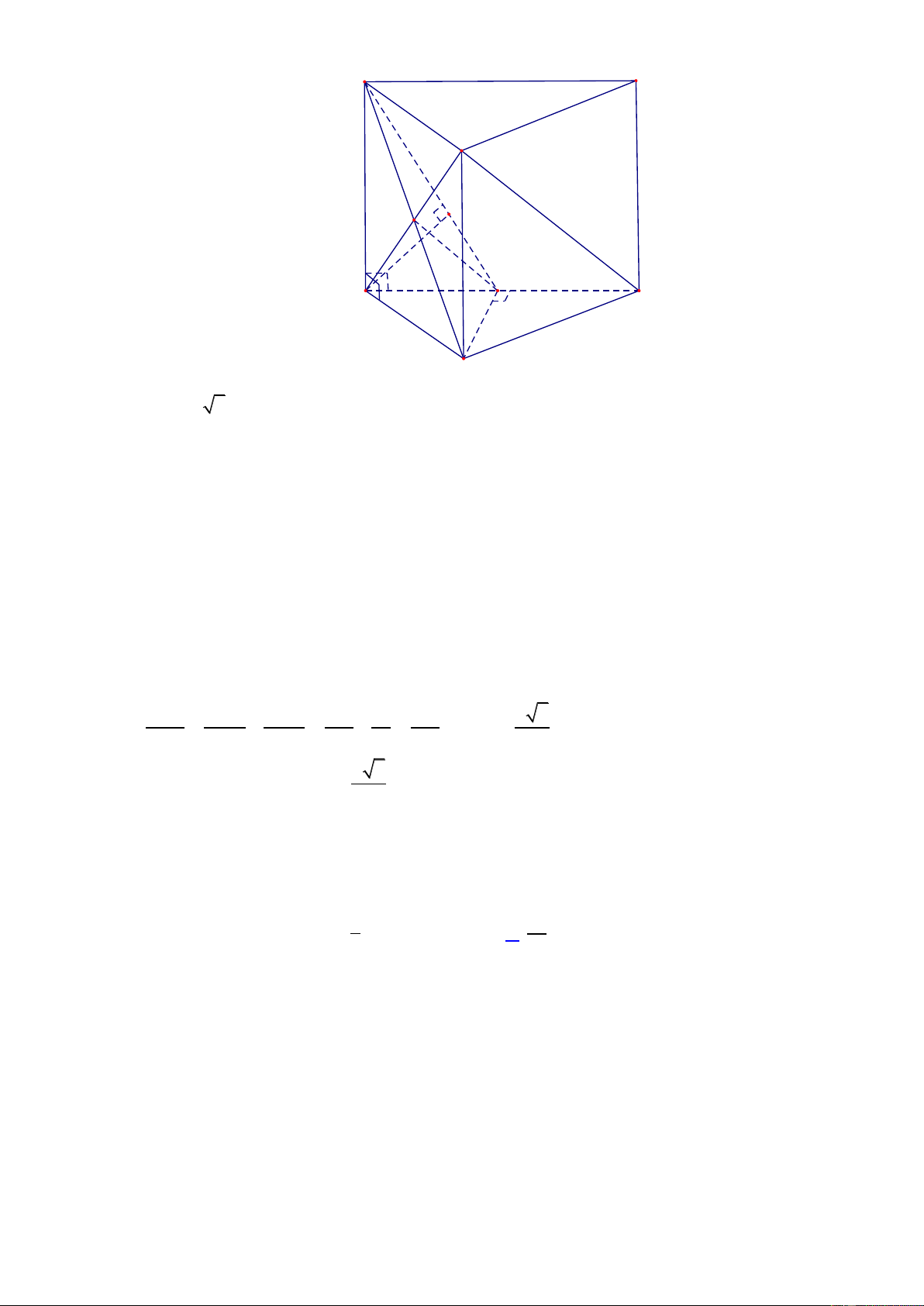
kính R tiếp xúc với 3 đường thẳng đó. Giá trị nhỏ nhất của R gần số nào nhất trong các số sau: A.2,1. B.2,2. C.2,3. D.2,4. Lời giải 
Ta có: d đi qua điểm A1;1 
;1 có VTCP u  2;1;  2 . 1   1    d
đi qua điểm B 3; 1; 2 có VTCP u  1; 2; 2 . 2   2    d
đi qua điểm C 4; 4 
;1 có VTCP u  2;  2;1 . 3   3       
Ta có u .u  0 , u .u  0 , u .u  0  d , d , d đôi một vuông góc với nhau. 3  2  1  1 2 2 3 3 1   
      u
 ,u .AB  0 , u
 ,u .BC  0, u
 ,u .CA  0  d , d , d đôi một chéo nhau. 3  2  1  1 2   2 3   3 1       
Lại có: AB  2;  2;  1 ; A .
B u  0 và A .
B u  0 nên d , d , d chứa 3 cạnh của hình 3  2  1  1 2
hộp chữ nhật như hình vẽ. B d2 d3 I A C d1
Vì mặt cầu tâm I  ; a ;
b c tiếp xúc với 3 đường thẳng d , d , d nên bán kính 3  2  1 
R d I, d d I, dd I,d 2 2
R d I,d  2
d I,d  2  d I,d 1 2  3 1   2  3   2       2 2 AI ,u  
 BI,u    CI,u      1    2    3    2 2 2 2     R            , ta thấy u u u 9 và      1 2 3 u   u   u  1   2   3     
AI  a 1;b 1;c  
1 ,  AI,u   2
b c  3;2a  2c  4;a  2b 1 . 1       
BI  a  3;b 1;c  2 , BI,u   2b  2c  6; 2a c  4;2a b  7 . 2       
CI  a  4;b  4;c   1 , C
I,u   b  2c 6; a  2c  2; 2
a  2b 16 . 3       2   2   2   2   2   2 2
9R   AI , u   BI , u   CI ,u  2
 27R  AI,u   BI,u   CI,u   1 2 3       1 2 3         2 2 2
18 a b c  126a  54b  54c  423 2 2 2  7   3   3  243 243  3 2 18 a  18 b  18 c           R  khi đó R  2,12 .  2   2   2  2 2 min 2 Trang24