Đề thi thử Toán (chung) vào 10 chuyên năm 2024 – 2025 phòng GD&ĐT TP Nam Định

UBND THÀNH PHỐ NAM ĐỊNH
ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025
Môn thi: Toán (chung) – Đề 1 ĐỀ THI THỬ
Dành cho học sinh thi vào các lớp chuyên tự nhiên
Thời gian làm bài 120 phút (Đề thi gồm 01 trang) Bài 1. (2,0 điểm) 1
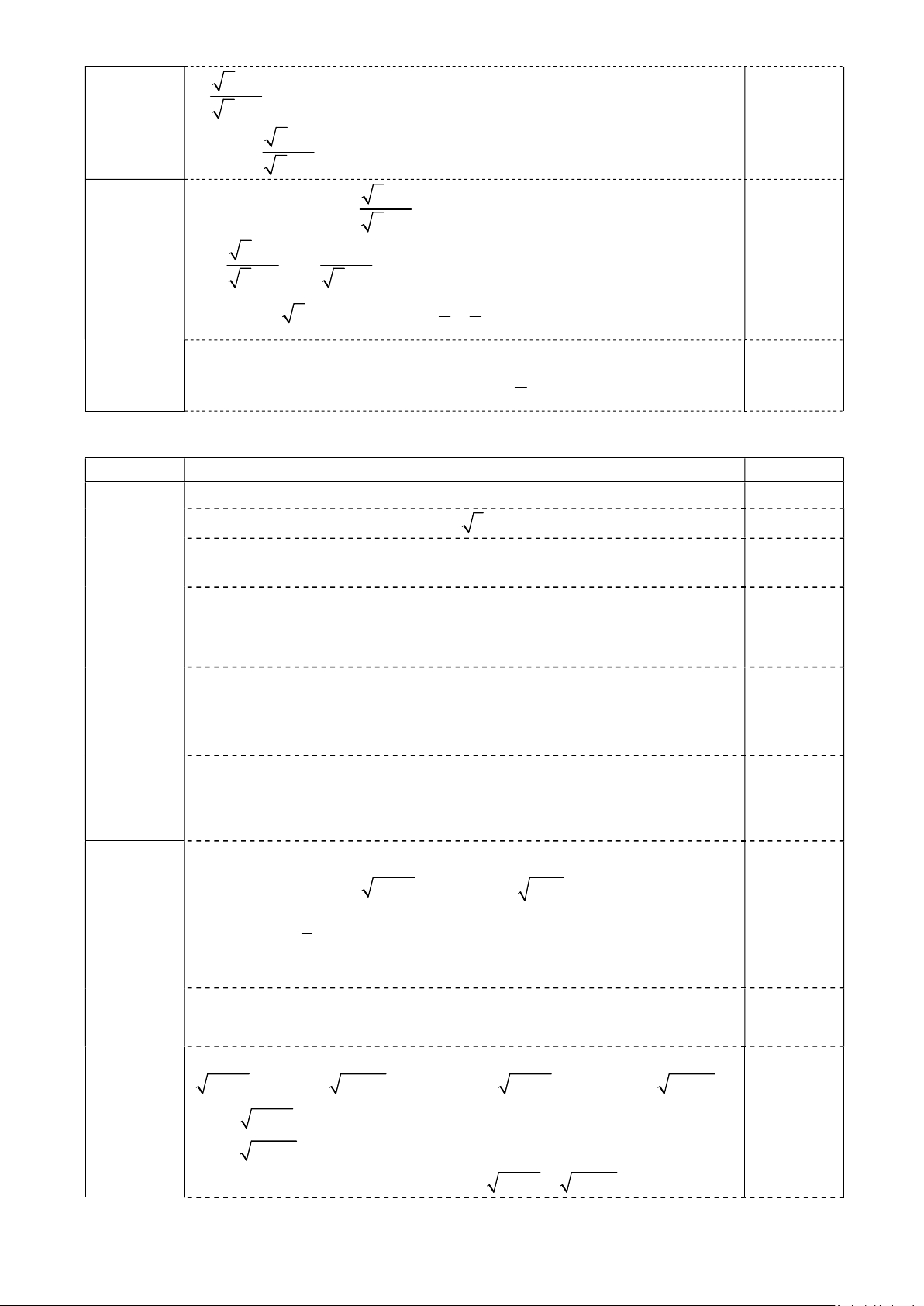
1. Tìm điều kiện xác định của biểu thức A  x 1  . 3  x 1
2. Tìm tất cả các giá trị của tham số m đề đường thẳng y  2
 x  m 1 cắt đường thẳng
y  2x  3 tại điểm nằm trên trục hoành.
3. Cho tam giác ABC nội tiếp O;3cm . Biết  0 B   0
70 ;C  50 ; Tính độ dài cung BC nhỏ.
4. Một chiếc bình thuỷ tinh hình trụ có chiều cao 30cm và đường kính đáy 20cm đựng
đầy nước. Tính số lít nước đựng trong bình (coi rằng thành bình và đáy bình mỏng). Bài 2. (1,5 điểm)  x  2 1 3 x  6  x  5 Cho biểu thức P     .  với x  0 . x 1 x 4 x 5 x 4      x  3  
a) Rút gọn biểu thức P .
b) Tìm giá trị lớn nhất của biểu thức P . Bài 3. (1,5 điểm) 1) Cho phương trình 2
x  2x  m 1  0 (m là tham số).
a) Giải phương trình với m 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x , x thoả mãn 1 2 2 x  x  2x . 1 2 2   2x  y  x  y   1  4 y   1  4  x
2) Giải hệ phương trình   3x 1  4  2x   1  y 1  3 . y Bài 4. (3,0 điểm)
Cho nửa đường tròn O; R , đường kính BC , A là điểm bất kì trên nửa đường tròn sao
cho AB  AC; A khác C . Kẻ AH vuông góc với BC tại H . Gọi M , N lần lượt là hình chiếu
vuông góc của H trên AB, AC . a) Chứng minh A .
B AM  AC.AN và tứ giác BCNM là tứ giác nội tiếp.
b) Đường thẳng MN cắt nửa đường tròn O; R tại các điểm E, F ( E thuộc cung AB
nhỏ), cắt đoạn thẳng AO tại D . Chứng minh OA  MN và AEH cân.
c) Đường thẳng MN cắt đường thẳng BC tại I , IA cắt nửa đường tròn O; R tại điểm
thứ hai là K ( K khác A ), KN cắt BC tại Q . Chứng minh 2 QH  QC.QI . Bài 5. (1,0 điểm) 1) Giải phương trình 2 x  x   2 2 2 1  12  3x 16x  3. 2) Cho ,
x y, z là các số dương thoả mãn xyz  1. Tìm giá trị lớn nhất của biểu thức 1 1 1 P    2 2 2 2 2 2
x  2y  3 y  2z  3 z  2x  3 -------HẾT-------
Họ và tên thí sinh:……………………………. Giám thị 1:…………………………………….
SBD:……………………………………………. Giám thị 2: ……………………………………. UBND THÀNH PHỐ NAM ĐỊNH
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT CHUYÊN
Môn thi: Toán (chung) – Đề 1
Dành cho học sinh thi vào các lớp chuyên tự nhiên
(Hướng dẫn chấm gồm 05 trang) Bài 1: (2,0 điểm) Câu Nội dung Điểm 1) x 1 0, 25 0,5 điểm 
ĐKXĐ của biểu thức là x  3   3 x 1  0
Tìm được 1  x  3; x  2 . 0,25 2)
Toạ độ giao điểm của đường thẳng y  2x  3 với trục hoành là 0,25 0,5 điểm  3  ;0    2  Vì 2  2
 , hai đường thẳng cắt nhau tại điểm nằm trên trục hoành 0,25  3  đường thẳng  y  2
 x  m 1 đi qua điểm ;0    2  3  0  2.  m 1  m  2 . 2 3) Tính được  0 BOC  120 0,25
0,5 điểm Tính được độ dài cung 120 BC nhỏ bằng ..3  2 cm 0,25 180 4)
Thể tích của nước đựng trong bình là 2 3 .10 .30  3000cm 0,25
0,5 điểm Số lít nước có trong bình là 3  9,42 (lít) 0,25 Bài 2 (1,5 điểm) Câu Nội dung Điểm 2) Với x  0 , ta có 0,25 1,0 điểm  x  2 1 3 x  6  x  5 P     .  x 1 x 4 x 5 x 4      x  3     x  2 1 3 x  6 x  5       x  x    x  1 x 4 . 1 4  x  3 
 x 2 x 4 x 13 x 6 x 5   x  1 x 4 . x 3
x  6 x  8  x 1 3 x  6 x  5 0,25   x  1 x 4 . x 3 x  4 x  3 x  5
  x  1 x 4. x 3  x  1 x 3 0,25 x  5   x   1  x  4. x 3 x  5 0,25  x  4 x  5 Vậy P  với x  0 x  4 x  5 0,25 Theo câu a) ta có P  với x  0 x  4 x  5 1 P   1 1b) x  4 x  4 0,5 điểm 1 5
Vì x  0  x  4  4  P  1  4 4
Dấu "  " xảy ra khi x  0 (thoả mãn điều kiện) 0,25 5
Vậy giá trị lớn nhất của biểu thức P bằng khi x  0 4 Bài 3: (2,5 điểm) Câu Nội dung Điểm 1)
1a) Với m  1, phương trình trở thành 2 x  2x  2  0 0,25
1,5 điểm Giải phương trình ta được x 1 3 . 0,25 1b) 2 x  2x  m 1  0 0,25
Phương trình có hai nghiệm phân biệt   '  0  m  2  0  m  2  x  x  2 1  0,25 1 2  
Áp dụng định lý Viét ta có  x x  m 1 2  1 2  
Từ x  x  2  x  2  x . Thay vào biểu thức 2 x  x  2x ta được 0,25 1 2 1 2 1 2 2 2 2  x  x  2x 2 2 2
Từ đó tìm được x  1  ; x  2 2 2 +) Với x  1
  x  3. Thay vào (2) tìm được m  2 (t/m) 0,25 2 1
+) Với x  2  x  0 . Thay vào (2) tìm được m  1  (t/m) 2 1
Kết luận: Tất cả các giá trị của tham số m cần tìm là m  2;m  1  . 2)   2x  y 
x  y  1  4 y  1  4  x  1 0,25
1,0 điểm Giải hệ phương trình   3x 1  4 
2x  1  y 1 3y 2  1 x  ĐKXĐ:  3 y 1
Biến đổi phương trình (1) ta được x  y   1 2x  y  4  0 0,25
Kết hợp ĐKXĐ suy ra 2x  y  4  0
Thay vào phương trình (2) ta có 0,25
3x 1  2x  8  2x  3  23x  
1  3x 1  22x  3  2x  3  3x 1  a Đặt 
a,b  0 ta được phương trình 2 2 2a  a  2b  b  2x  3  b
Giải phương trình tìm được a  b  3x 1  2x  3
Giải phương trình tìm được x  4 . Từ đó tìm được y  12 . 0,25
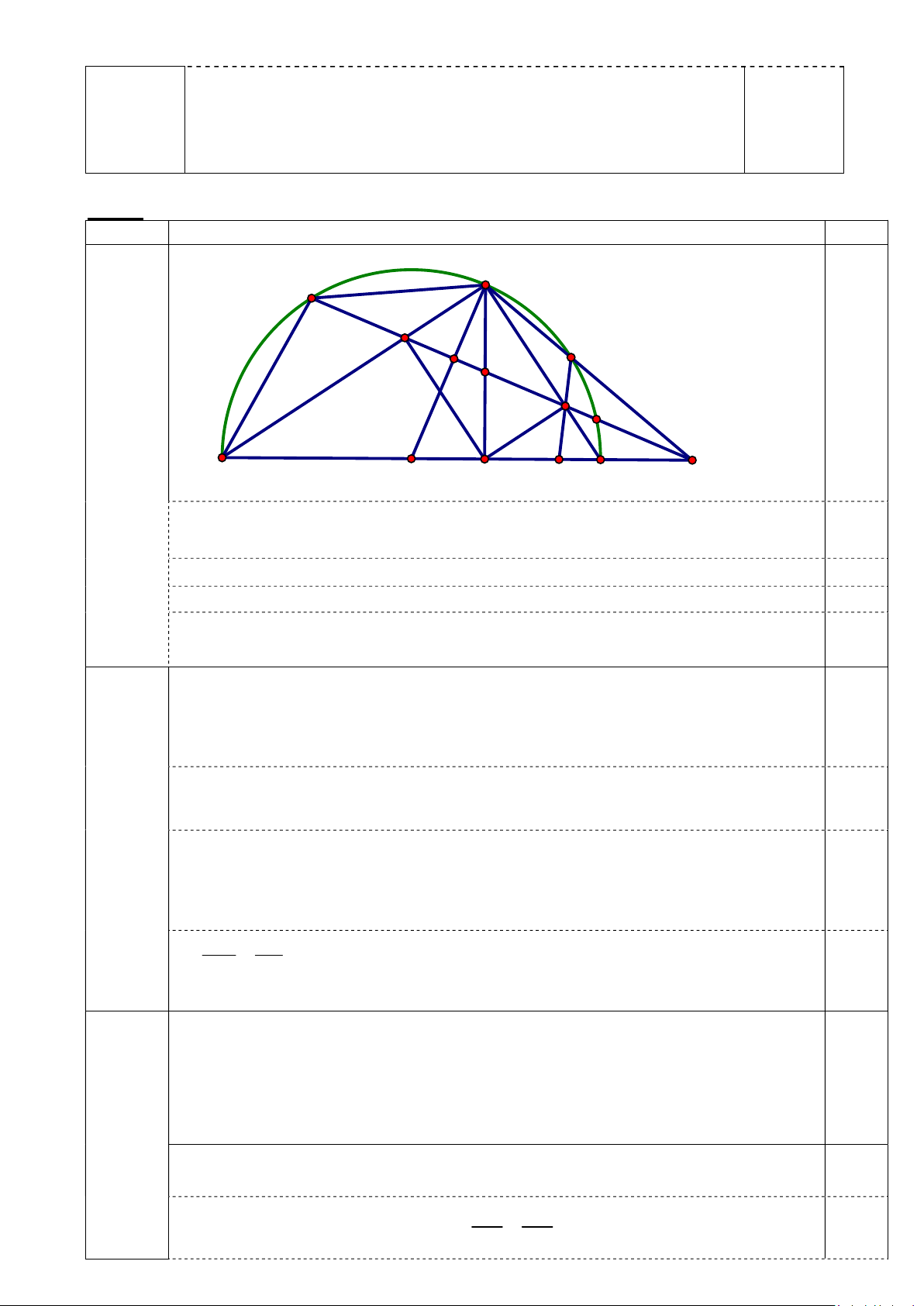
Kết hợp điều kiện và kết luận: Tất cả các nghiệm của hệ phương x  4 trình là  . y  12 Bài 4: (3,0 điểm) Câu Nội dung Điểm A E M 1) 1,0 D K điểm G N F B O H Q I C
Tam giác AHB vuông tại H có 2 HM  AB  AH  A . B AM 0,25
Tam giác AHC vuông tại H có 2 HN  AC  AH  AC.AN Từ đó suy ra A . B AM  AC.AN 0,25 Chứng minh A  MN  A  CB 0,25   AMN   ACB 0,25
Từ đó suy ra tứ giác BCNM nội tiếp. 2)
Tam giác OAB cân tại O   OAB   OBA 0,25 Theo câu a) ta có  AMN   ACB   AMN   OAB   ABC   ACB
Tam giác ABC vuông tại A có  ABC   0 ACB  90 0,25   AMD   0 DAM    0 90 ADM  90  AO  MN
Ta có AO  MN nên A là điểm chính giữa của cung E F 0,25  AEM   Suy ra ABE
Chứng minh được AME  A  EB g.g AM AE 2    0,25 A . B AM  AE AE AB Mà 2 AH  A . B AM suy ra 2 2 AH  AE  AH  AE  A  EH cân. 3) Chứng minh IC.IB  IK.IA 0,25
Mà IC.IB  IM .IN  IK.IA  IM .IN Chứng minh I  KN  I  MA .cg.c   IKN   IMA
Suy ra tứ giác AMNK nội tiếp, suy ra 4 điểm ,
A M , N, K cùng thuộc một đường tròn. Chứng minh 4 điểm ,
A M , H , N cùng thuộc một đường tròn 0,25 Từ đó suy ra 5 điểm ,
A M , H , N, K cùng thuộc một đường tròn. QH QN 0,25 Chứng minh Q  HN  Q  KH g g 2 .    QH  QN.QK (1) QK QH  IKN   Ta có IMA , mà  AMN   ACB cmt   IKN   ACB   IKQ   NCQ QN QC 0,25
Từ đó chứng minh được Q  NC  Q  IK g.g    QN.QK  QI.QC QI QK (2) 2
Từ (1) và (2) suy ra QH  QC.QI Câu 5: (1.0 điểm) Câu Nội dung Điểm 1. ĐKXĐ: 2
12  3x  0  2  x  2 0,5
Biến đổi phương trình trở thành 0,25 điểm 3 2 2
4x  2x 15x  6  12  3x  x  3 2 2       x x x x  2 12 3 6 9 2 4x  6x  3    2 12  3x  x  3    1  2
4x  6x  3x  2    0 2  12  3x   x 3 1 0,25
Với 2  x  2 ta có  x  2   0 2 12  3x  x  3  3  21 x  Do đó 2 4 4x  6x  3  0  
t / m (thoả mãn điều kiện)  3  21 x   4 3 21 3 21
Kết luận: Tập nghiệm của phương trình là  ;  .  4 4   2. Ta có 2 2 x  y    2 2 x  y    2 2 3 y   1  2  2xy  2y  2 0,5 1 1 điểm Suy ra  0,25 2 2
x  2y  3 2xy  2y  2
Chứng minh tương tự ta được 1 1 1 1  ;  2 2 2 2
y  2z  3 2yz  2z 1 z  2x  3 2zx  2x 1 Từ đó suy ra 1 1 1 1 1 1      2 2 2 2 2 2 x  2y  3
y  2z  3 z  2x  3 2xy  2 y  2 2 yz  2z  2 2zx  2x  2 1  1 1 1      
2  xy  y 1 yz  z 1 zx  x 1 1 1 1
Chứng minh được với xyz  1 thì   1
xy  y 1 yz  z 1 zx  x 1 1 0,25
Từ đó suy ra P  . Dấu bằng xảy ra  x  y  z  1 2 1
Vậy giá trị lớn nhất của biểu thức P bằng khi x  y  z  1. 2 Chú ý :
1) Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày,
nếu học sinh giải theo cách khác mà đúng và đủ các bước thì cho điểm tương đương.
2) Bài 4: Học sinh bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu hình vẽ sai ở phần
nào thì không cho điểm phần lời giải liên quan đến hình của phần đó.
3) Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn. ------HẾT------ UBND THÀNH PHỐ NAM ĐỊNH
ĐỀ THI TUYỂN SINH LỚP 10 THPT CHUYÊN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2024 - 2025
Môn thi: Toán (chung) – Đề 2 ĐỀ THI THỬ
Dành cho học sinh thi vào các lớp chuyên xã hội
Thời gian làm bài 120 phút (Đề thi gồm 01 trang) Bài 1. (2,0 điểm) 1
1. Tìm điều kiện xác định của biểu thức A  x 1  . 3  x
2. Tìm tất cả các giá trị của tham số m đề đường thẳng y  2
 x  m 1 cắt đường thẳng
y  2x  3 tại điểm nằm trên trục tung.
3. Cho tam giác ABC nội tiếp O;3cm . Biết  0 B   0
70 ;C  50 ; Tính độ dài cung BC nhỏ.
4. Một chiếc bình thuỷ tinh hình trụ có chiều cao 30cm và đường kính đáy 20cm đựng
đầy nước. Tính số lít nước đựng trong bình (coi rằng thành bình và đáy bình mỏng). Bài 2. (1,5 điểm)  x  2 1 3 x  6  x  5 Cho biểu thức P     .  với x  0 . x 1 x 4 x 5 x 4      x  3  
a) Rút gọn biểu thức P .
b) Tìm giá trị lớn nhất của biểu thức P . Bài 3. (1,5 điểm) 1) Cho phương trình 2
x  2x  m 1  0 (m là tham số).
a) Giải phương trình với m 1.
b) Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x , x thoả mãn 1 2 2 x  2x  m  7  0 . 1 2 2 2x  6y  7x y
2) Giải hệ phương trình  2x  y  4  0. Bài 4. (3,0 điểm)
Cho nửa đường tròn O; R , đường kính BC , A là điểm bất kì trên nửa đường tròn sao
cho AB  AC; A khác C . Kẻ AH vuông góc với BC tại H . Gọi M , N lần lượt là hình chiếu
vuông góc của H trên AB, AC . a) Chứng minh A .
B AM  AC.AN và tứ giác BCNM là tứ giác nội tiếp.
b) Đường thẳng MN cắt nửa đường tròn O; R tại các điểm E, F ( E thuộc cung AB
nhỏ), cắt đoạn thẳng AO tại D . Chứng minh OA  MN và AEH cân. c) Chứng minh 1 1 1   . AD BH CH Bài 5. (1,0 điểm)
1) Giải phương trình x x   2 4 7  12  3x . 2) Cho ,
a b là các số thực không âm thoả mãn 2 2
a  b  4 . Tìm giá trị lớn nhất của biểu thức ab M  . a  b  2 -------HẾT-------
Họ và tên thí sinh:……………………………. Giám thị 1:…………………………………….
SBD:……………………………………………. Giám thị 2: ……………………………………. UBND THÀNH PHỐ NAM ĐỊNH
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI THỬ TUYỂN SINH LỚP 10 THPT CHUYÊN
Môn thi: Toán (chung) – Đề 2
Dành cho học sinh thi vào các lớp chuyên xã hội
(Hướng dẫn chấm gồm 05 trang) Bài 1: (2,0 điểm) Câu Nội dung Điểm 1) x 1 0, 25 0,5 điểm 
ĐKXĐ của biểu thức là x  3   3  x  0 Tìm được 1 x  3 . 0,25 2) Vì 2  2
 , hai đường thẳng cắt nhau tại điểm nằm trên trục tung 0,25 0,5 điểm  m13  m  4 0,25
Vậy tất cả các giá trị của tham số m để hai đường thẳng cắt nhau tại
điểm nằm trên trục tung là m  4. 3) Tính được  0 BOC  120 0,25
0,5 điểm Tính được độ dài cung 120 BC nhỏ bằng ..3  2 cm 0,25 180 4)
Thể tích của nước đựng trong bình là 2 3 .10 .30  3000cm 0,25
0,5 điểm Số lít nước có trong bình là 3  9,42 (lít) 0,25 Bài 2. (1,5 điểm) Câu Nội dung Điểm 2) Với x  0 , ta có 0,25 1,0 điểm  x  2 1 3 x  6  x  5 P     .  x 1 x 4 x 5 x 4      x  3     x  2 1 3 x  6 x  5       x  x    x  1 x 4 . 1 4  x  3 
 x 2 x 4 x 13 x 6 x 5   x  1 x 4 . x 3
x  6 x  8  x 1 3 x  6 x  5 0,25   x  1 x 4 . x 3 x  4 x  3 x  5
  x  1 x 4. x 3  x  1 x 3 0,25 x  5   x   1  x  4. x 3 x  5 0,25  x  4 x  5 Vậy P  với x  0 x  4 x  5 0,25 Theo câu a) ta có P  với x  0 x  4 x  5 1 P   1 1b) x  4 x  4 0,5 điểm 1 5
Vì x  0  x  4  4  P  1  4 4
Dấu "  " xảy ra khi x  0 (thoả mãn điều kiện) 0,25 5
Vậy giá trị lớn nhất của biểu thức P bằng khi x  0 4 Bài 3: (2,5 điểm) Câu Nội dung Điểm 1)
2a) Với m  1, phương trình trở thành 2 x  2x  2  0 0,25 1,5
Giải phương trình ta được x 1 3 . 0,25
điểm 2b) 2x 2xm1 0 0,25
Phương trình có hai nghiệm phân biệt   '  0  m  2  0  m  2  x  x  2 1  0,25 1 2  
Áp dụng định lý Viét ta có  x x  m 1 2  1 2  
Từ x  x  2 . Thay vào biểu thức 2
x  2x  m  7  0 ta được 0,25 1 2 1 2
x   x  x  x  m  7  0   x  x 2 2  x x  m  7  0 (3) 1 1 2 2 1 2 1 2
Từ (1), (2), (3) ta có 4  m 1 m  7  0  m  1 (thoả mãn đk) 0,25
Kết luận: Tất cả các giá trị của tham số m cần tìm là m  1. 2) 2 2x  6y  7x y   1 0,25 1,0
Giải hệ phương trình  2x  y  4  0.  2 điểm x   ĐKXĐ:  y  0 x  y 0,25
Biến đổi phương trình (1) ta được x  y  x  y  2 2 2 3  0   2x  3 y 
+) TH x  2 y , thay vào phương trình (2) ta được 0,25  y  2  2 2 y  4 y  4  0  
 y 12 8 2 t / m  x  4   4 2  y  2  2 2  loai
+) TH 2x  3 y , thay vào phương trình (2) ta được 0,25  y 1 t / m y  3 y  4  0    y  4   loai Với 3 y  1  y  1 x  2  3
x  4  4 2 x 
Kết luận: Tất cả các nghiệm của hệ phương trình là  ; 2 .
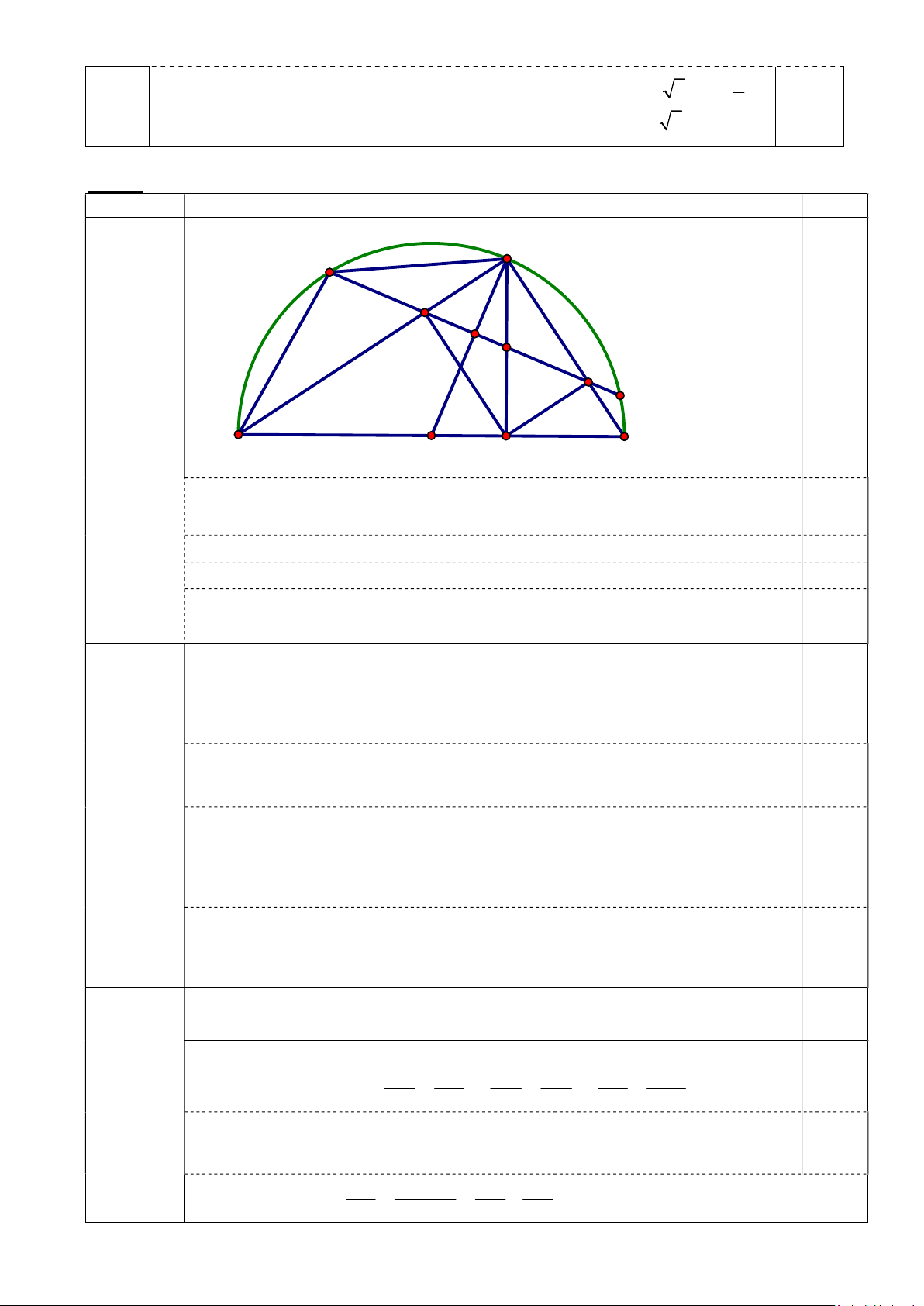
y 12 8 2 y 1 Bài 4: (3,0 điểm) Câu Nội dung Điểm A E M 1) 1,0 D điểm G N F B O H C
Tam giác AHB vuông tại H có 2 HM  AB  AH  A . B AM 0,25
Tam giác AHC vuông tại H có 2 HN  AC  AH  AC.AN Từ đó suy ra A . B AM  AC.AN 0,25 Chứng minh A  MN  A  CB 0,25   AMN   ACB 0,25
Từ đó suy ra tứ giác BCNM nội tiếp. 2a)
Tam giác OAB cân tại O   OAB   OBA 0,25 Theo câu a) ta có  AMN   ACB   AMN   OAB   ABC   ACB
Tam giác ABC vuông tại A có  ABC   0 ACB  90 0,25   AMD   0 DAM    0 90 ADM  90  AO  MN
Ta có AO  MN nên A là điểm chính giữa của cung E F 0,25  AEM   Suy ra ABE
Chứng minh được AME  A  EB g.g AM AE 2    0,25 A . B AM  AE AE AB Mà 2 AH  A . B AM suy ra 2 2 AH  AE  AH  AE  A  EH cân. 2b)
Gọi G là giao điểm của MN và AH . 0,25
Chứng minh tứ giác AMHN là hình chữ nhật  AG  GH Chứng minh 0,25     g AD AG AD AH 1 BC ADG AHO g.       (1) 2 AH AO AH BC AD AH 0,25 2
Tam giác ABC vuông tại A có AH  BC  AH  BH.CH (2) 1 BC 1 1 0,25 Từ (1) và (2) suy ra    AD BH.CH BH CH Bài 5: (1.0 điểm) Câu Nội dung Điểm 1. ĐKXĐ 2
12  3x  0  2  x  2 0,5
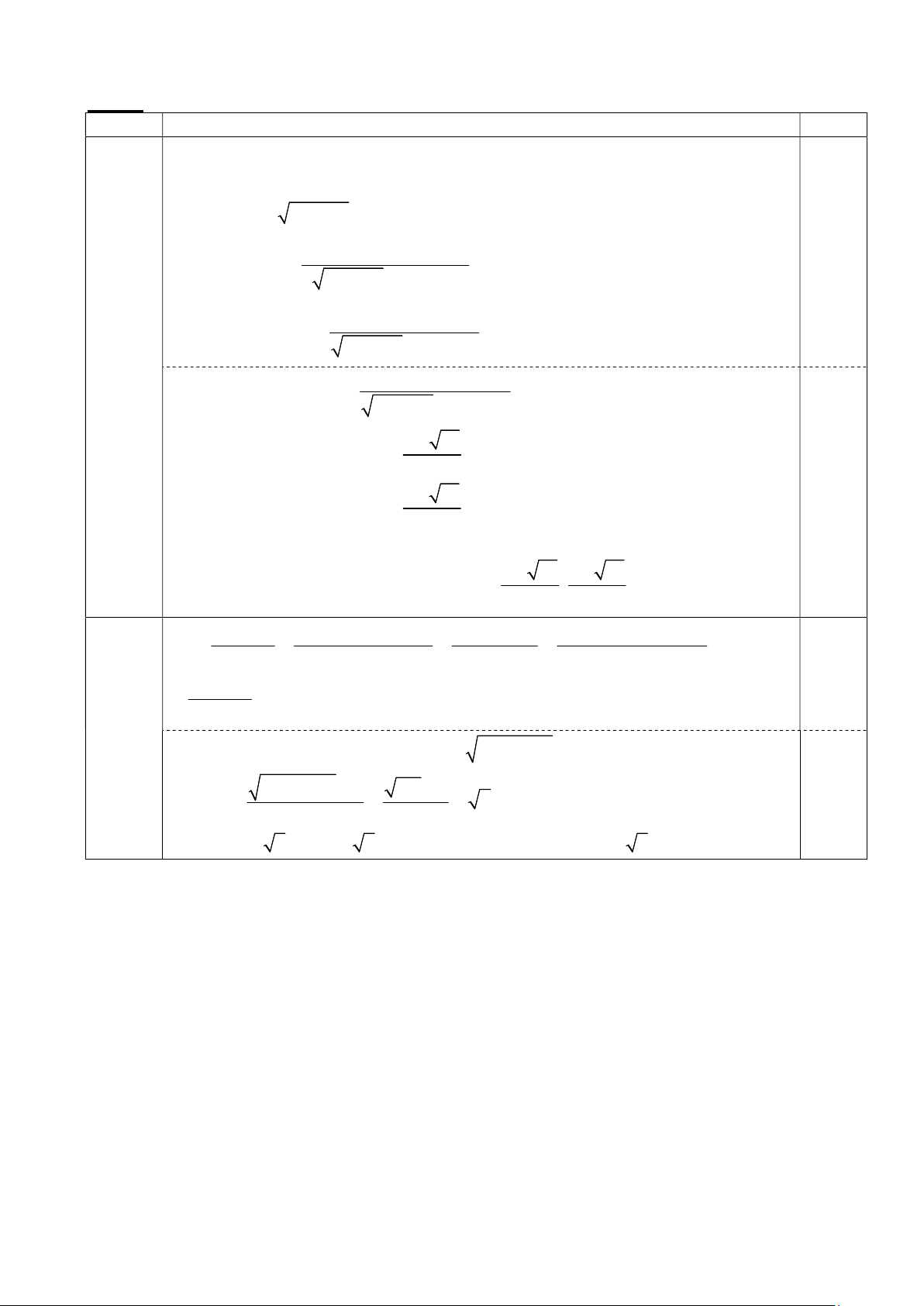
Biến đổi phương trình trở thành 0,25 điểm 2 2
4x  6x  3  12  3x  x  3 2 12  3x   2 x  6x  9 2   4x  6x  3  2 12  3x  x  3    1  2 4x  6x  3 1     0 2  12  3x   x  3 1 0,25
Với 2  x  2 ta có 1  0 2 12  3x  x  3  3  21 x  Do đó 2 4 4x  6x  3  0   t / m  3  21 x   4 3 21 3 21
Kết luận: Tập nghiệm của phương trình là  ;  .  4 4   2. 2 2 2 2 ab (a  b)  (a  b ) (a  b)  4 (a  b  2)(a  b  2) 0,5 M     a  b  2 2(a  b  2) 2(a  b  2) 2(a  b  2) điểm a  b  2 0,25  2 Ta có: 2 2 2 2 2 (a  )
b  2(a  b )  a  b  2(a  b ) 2 2 2(a  b )  2 2.4  2 0,25 Vậy M    2 1 2 2
Khi a = b = 2 thì M = 2 -1. Vậy giá trị lớn nhất của M là 2 -1 Chú ý :
1) Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày,
nếu học sinh giải theo cách khác mà đúng và đủ các bước thì cho điểm tương đương.
2) Bài 4: Học sinh bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu hình vẽ sai ở phần
nào thì không cho điểm phần lời giải liên quan đến hình của phần đó.
3) Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn. ------HẾT------
Document Outline

• Đề 1- KHTN
• Đề 2- KHXH